Abstract
The paper focuses on a recent challenge brought forward against the interventionist approach to the meaning of counterfactual conditionals. According to this objection, interventionism cannot account for the interpretation of right-nested counterfactuals, the problem being its strict interventionism. We will report on the results of an empirical study supporting the objection. Furthermore, we will extend the well-known logic of intervention with a new operator expressing an alternative notion of intervention that does away with strict interventionism (and thus can account for some critical examples). This new notion of intervention operates on the valuation of the variables in a causal model, and not on their functional dependencies.




Similar content being viewed by others
Notes
If the counterfactual’s antecedent were allowed to be an arbitrary Boolean combination of atoms, this step would already produce more than one alternative. This generalisation can be dealt with as in Briggs (2012), which relies on Fine (2012) to provide a procedure for generating all these models. However, the issue of the number of models is orthogonal to this text’s main focus. Therefore, we keep the restriction on the form of the antecedent, as done in Pearl (2000) and Halpern (2013).
Note: the valuation is unique, not only because the values of exogenous variables is determined, but also because, if \(\langle {\mathcal {S}}, {\mathcal {A}} \rangle \) is recursive, so is \(\langle {\mathcal {S}}_{\overrightarrow{X} {=}\overrightarrow{x}}, {\mathcal {A}}^{{\mathcal {S}}_{\overrightarrow{X} {=}\overrightarrow{x}}} \rangle \). This is because the intervention operation only removes causal dependencies, and thus no circular dependencies are added.
Within defeasible reasoning Koons (2017), A3 is known as the principle of weak/cautious monotonicity (adding conclusions as premises does not invalidate conclusions) Gabbay (1984); Makinson (1988). Together with the cut principle Kraus et al. (1990) (removing premises that are also conclusions does not invalidate conclusions, \(\left( [\overrightarrow{X}{=}\overrightarrow{x}, Y{=}y](Z{=}z) \wedge [\overrightarrow{X}{=}\overrightarrow{x}](Y{=}y) \right) \rightarrow [\overrightarrow{X}{=}\overrightarrow{x}](Z{=}z)\), also valid), it makes an intervention cumulative: if \([\overrightarrow{X}{=}\overrightarrow{x}]\) sets Y to y, then it has the same effects as \([\overrightarrow{X}{=}\overrightarrow{x}, Y{=}y]\).
For the syntactic characterisation of direct dependency \(\rightarrowtail \), recall that, for \(V \in {\mathcal {V}}\) and \(X \in {\mathcal {U}}\cup {\mathcal {V}}\), we have \(X \rightarrowtail V\) if and only if there are values \(\overrightarrow{z}\) of variables in \(\overrightarrow{Z} = ({\mathcal {U}}\cup {\mathcal {V}}) \setminus \{ X, V \}\) and two different values \(x_1, x_2\) of X such that the value V gets by setting \((\overrightarrow{Z},X)\) to \((\overrightarrow{z}, x_1)\) is different from the value it gets by setting the same variables to \((\overrightarrow{z}, x_2)\). This can be expressed by the formula
$$\begin{aligned} \bigvee _{ \begin{array}{l} \overrightarrow{z} \in {\mathcal {R}}( ({\mathcal {U}}\cup {\mathcal {V}}) \setminus \{ X,V \}), \\ \{ x_1,x_2 \} \subseteq {\mathcal {R}}(X),\, x_1 \ne x_2, \\ \{ v_1, v_2 \} \subseteq {\mathcal {R}}(V),\, v_1 \ne v_2 \end{array} } [\overrightarrow{Z}{=}\overrightarrow{z},X{=}x_1](V{=}v_1) \;\wedge \; [\overrightarrow{Z}{=}\overrightarrow{z},X{=}x_2](V{=}v_2), \end{aligned}$$which is abbreviated as \(X \rightsquigarrow V\) (cf. with the syntactic definition of causal dependency in Halpern (2000)).
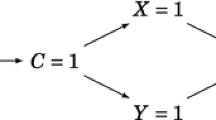
Fisher also considers an example with the counterfactual “If the match were struck and it lit, then if it hadn’t been struck, it would have lit”. This is not a good example to make his point, as it contains a conjunction of cause (striking the match) and effect (the match lights) in the antecedent. For the counterexample to work, Fisher needs this conjunction to be interpreted as two independent interventions. However, it could be that “and” is interpreted causally in this case: “If the match were struck and because of that it lit, ...”. But then the fact that the match lights would be introduced as a causal consequent of the striking of the match and not as an independent intervention.
We ignore other possible variables, as they will not affect the relevant predictions made.
Fisher discusses in Fisher (2017) an alternative definition of intervention, dubbed “side-constrained intervention”, but admits that this variation is not really targeting the root of the problem.
A good example are backtracking counterfactuals: counterfactuals that reason backward in time. The interventionist approach predicts all backtracking to be impossible. However, sometimes backtracking seems to be possible. This is occasionally explained by distinguishing a possible epistemic reading that allows for backtracking.
Thus, in particular, our notion of intervention will not allow for abductive reasoning from effect to cause.
In other words, there might be variables whose values diverge from what is predicted by their structural function when applied to the values of their causal parents.
The model is recursive so, from \({\mathcal {S}}\)’s induced causal graph \(\langle {\mathcal {U}}\cup {\mathcal {V}}, \rightarrowtail \rangle \) and the antecedent \(\overrightarrow{X}{=}\overrightarrow{x}\), one can create a chain of sets of variables \(S_0 \subset \cdots \subset S_k\) where \(S_0 = {\mathcal {U}}\cup \overrightarrow{X}\), \(S_k={\mathcal {U}}\cup {\mathcal {V}}\) and, for any \(S_i\) and \(S_{i+1}\), the value of variables in \(S_{i+1} \setminus S_i\) can be calculated from \({\mathcal {S}}\) and the value of variables in \(S_{i}\). Since the values \({\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}}\) assigns to variables in \(S_0\) are fixed (from the initial valuation \({\mathcal {A}}\) and the antecedent \(\overrightarrow{X}{=}\overrightarrow{x}\)), the values of the rest can be properly obtained.
Note: when the original valuation \({\mathcal {A}}\) complies with the causal dependencies in \({\mathcal {S}}\), both strategies produce the same result.
Note: our setting allows intervention on exogenous variables, so S can be taken to be exogenous, thus making U superfluous. Still, U is kept, in line with the common modelling strategy of representing external factors by means of exogenous variables.
This principle is sometimes also called the Weak Import-Export Principle, while the principle without the restriction of non-common variables is called Import-Export Principle Fisher (2017).
But see Starr (2014) for a dynamic semantic implementation of the similarity analysis that does validate the Import-Export Principle.
In this case the order in which the interventions are performed has no effect on the resulting model. This is because an intervention, as defined here, only affects the value of a variable if the variable is intervened or if it causally depends on an intervened variable.
The ‘small variation’ detail refers to the fact that, although we do have an axiom system for the fragment of
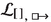 without non-strict intervention (Sect. 2), the system characterises validities over a different class of models: causal models. In this particular case this is not a problem, the reason being that the setting of this section is a conservative extension of that in Sect. 2. Indeed, atoms, Boolean operators and \([\;]\) are interpreted as before. The class of models does change, but this affects neither atoms nor Boolean operators. Crucially, strict interventions force the valuation to agree with the structural functions, so formulas occurring under their scope behave just as in a causal model. The reduction translates non-strict interventions into strict ones, so this is enough.
without non-strict intervention (Sect. 2), the system characterises validities over a different class of models: causal models. In this particular case this is not a problem, the reason being that the setting of this section is a conservative extension of that in Sect. 2. Indeed, atoms, Boolean operators and \([\;]\) are interpreted as before. The class of models does change, but this affects neither atoms nor Boolean operators. Crucially, strict interventions force the valuation to agree with the structural functions, so formulas occurring under their scope behave just as in a causal model. The reduction translates non-strict interventions into strict ones, so this is enough.The syntactic characterisation of causal dependency \(\rightarrowtail ^+\) relies in that of \(\rightarrowtail \). Indeed, given that \(\vert {\mathcal {U}}\vert = m\) and \(\vert {\mathcal {V}}\vert = n\), the fact that V is causally dependent on X can expressed by the formula
$$\begin{aligned} (X \rightsquigarrow V) \;\vee \; \bigvee _{k=1}^{m+n-2} \bigvee _{\big \{ \langle X_1, \ldots , X_{k}\rangle \;\mid \; X_i \in ({\mathcal {U}}\cup {\mathcal {V}}\setminus \{ X,V \}) \big \} } \Big ( (X \rightsquigarrow X_1)\ \wedge \bigwedge _{j=1}^{k-1} (X_{j} \rightsquigarrow X_{j+1}) \wedge (X_{k} \rightsquigarrow V) \Big ) \end{aligned}$$which is abbreviated as \(X \rightsquigarrow ^+ V\). Note how, while k runs over the number of needed intermediate variables (at least 1, and at most \(m+n-2\)), the intermediate disjunct runs over all possible tuples of k variables.
Thus, the generalisation rule for non-strict intervention is not required. For details on this, see Wang and Cao (2013) (in particular, Theorem 11).
Except in the case that the antecedent explicitly denies a certain law.
The questionnaire and data are available at https://osf.io/5t4uf/.
Axioms D0-D11 here are written in our style. Note that (i) \(\langle \overrightarrow{X}{=}\overrightarrow{x}\rangle \phi \) abbreviates \(\lnot [\overrightarrow{X}{=}\overrightarrow{x}]\lnot \phi \), and (ii) for \(\overrightarrow{X} = (X_1, \ldots , X_k)\) and \(\overrightarrow{x} = (x_1, \ldots , x_k)\), occurrences of \(\overrightarrow{X}{=}\overrightarrow{x}\) outside intervention operators abbreviate the conjunction \(X_1{=}x_1 \wedge \cdots \wedge X_k{=}x_k\). The version of D11 shown here looks drastically different from the original, mainly because it includes nested interventions, which are forbidden in \({\mathcal {L}}^+\). Yet, our version is correct, as atoms in \({\mathcal {L}}^+\), expressions of the form \(Y(\overrightarrow{u}){=}y\), essentially allow for interventions on exogenous variables (changes in the values of variables in \({\mathcal {U}}\)) to occur within the scope of interventions on endogenous variables \([\overrightarrow{X}{=}\overrightarrow{x}]\).
By definition, \(\langle \overrightarrow{X}{=}\overrightarrow{x}\rangle \phi \leftrightarrow \lnot [\overrightarrow{X}{=}\overrightarrow{x}]\lnot \phi \); by A7.1, \([\overrightarrow{X}{=}\overrightarrow{x}]\lnot \phi \leftrightarrow \lnot [\overrightarrow{X}{=}\overrightarrow{x}]\phi \). Thus, by propositional reasoning (from \(A \leftrightarrow \lnot B\) and \(B \leftrightarrow C\) derive \(A \leftrightarrow \lnot C\)), it follows that \(\langle \overrightarrow{X}{=}\overrightarrow{x}\rangle \phi \leftrightarrow \lnot \lnot [\overrightarrow{X}{=}\overrightarrow{x}]\phi \) and hence, by propositional reasoning once again (from \(A \leftrightarrow \lnot \lnot B\) infer \(A \leftrightarrow B\)), the required \(\langle \overrightarrow{X}{=}\overrightarrow{x}\rangle \phi \leftrightarrow [\overrightarrow{X}{=}\overrightarrow{x}]\phi \) is obtained.
From A7.1 we get \([\overrightarrow{X}{=}\overrightarrow{x}]\lnot (\phi \wedge \lnot \psi ) \leftrightarrow \lnot [\overrightarrow{X}{=}\overrightarrow{x}](\phi \wedge \lnot \psi )\); from A7.2 we get \([\overrightarrow{X}{=}\overrightarrow{x}](\phi \wedge \lnot \psi ) \leftrightarrow ([\overrightarrow{X}{=}\overrightarrow{x}]\phi \wedge [\overrightarrow{X}{=}\overrightarrow{x}]\lnot \psi )\). Then, by propositional reasoning, \([\overrightarrow{X}{=}\overrightarrow{x}]\lnot (\phi \wedge \lnot \psi ) \leftrightarrow \lnot ([\overrightarrow{X}{=}\overrightarrow{x}]\phi \wedge [\overrightarrow{X}{=}\overrightarrow{x}]\lnot \psi )\), that is (axiom A7.1 and propositional reasoning), \([\overrightarrow{X}{=}\overrightarrow{x}]\lnot (\phi \wedge \lnot \psi ) \leftrightarrow \lnot ([\overrightarrow{X}{=}\overrightarrow{x}]\phi \wedge \lnot [\overrightarrow{X}{=}\overrightarrow{x}]\psi )\). Hence, by the definition of “\(\rightarrow \)”, it follows that \([\overrightarrow{X}{=}\overrightarrow{x}](\phi \rightarrow \psi ) \rightarrow ([\overrightarrow{X}{=}\overrightarrow{x}]\phi \rightarrow [\overrightarrow{X}{=}\overrightarrow{x}]\psi )\).
References
Baltag, A., Moss, L. S., & Solecki, S. (1998). The logic of public announcements, common knowledge, and private suspicions. In I. Gilboa (Ed.), TARK (pp. 43–56). San Francisco, Morgan Kaufmann.
Barbero, F., Sandu, G. (2019). Interventionist counterfactuals on causal teams. In: B. Finkbeiner, S. Kleinberg (Eds.), Proceedings 3rd workshop on formal reasoning about causation, responsibility, and explanations in science and technology, Thessaloniki, Greece, 21st April 2018. Volume 286 of Electronic Proceedings in theoretical computer science, pp 16–30. Open Publishing Association
Briggs, R. (2012). Interventionist counterfactuals. Philosophical Studies, 160(1), 139–166.
Ciardelli, I., Zhang, L., & Champollion, L. (2018). Two switches in the theory of counterfactuals. Linguistics and Philosophy: A study of truth conditionality and minimal change.
Etlin, D.J. (2008). Desire, belief, and conditional belief. PhD thesis, Massachusetts Institute of Technology
Fine, K. (2012). Counterfactuals without possible worlds. The Journal of Philosophy, 109(3), 221–246.
Fisher, T. (2017). Causal counterfactuals are not interventionist counterfactuals. Synthese, 194(12), 4935–4957.
Gabbay, D. M. (1984). Theoretical foundations for non-monotonic reasoning in expert systems. In: K. R. Apt (Ed.), Logics and models of concurrent systems—conference proceedings, colle-sur-loup (near nice), France, 8-19 October 1984. Volume 13 of NATO ASI Series (pp. 439–457). Springer.
Galles, D., & Pearl, J. (1997). Axioms of causal relevance. Artificial Intelligence, 97(1–2), 9–43.
Galles, D., & Pearl, J. (1998). An axiomatic characterization of causal counterfactuals. Foundations of Science, 3(1), 151–182.
Halpern, J. Y. (2016). Actual causality. MIT Press.
Halpern, J. Y. (2000). Axiomatizing causal reasoning. Journal of Artificial Intelligence Research, 12, 317–337.
Halpern, J. Y. (2013). From causal models to counterfactual structures. The Review of Symbolic Logic, 6(2), 305–322.
Kaufmann, S. (2005). Conditional predictions. Linguistics and Philosophy, 28(2), 181–231.
Kaufmann, S. (2013). Causal premise semantics. Cognitive Science, 37, 1136–1170.
Koons, R. (2017). Defeasible reasoning. In: E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy. Winter 2017 edn. Metaphysics Research Lab, Stanford University
Kraus, S., Lehmann, D., & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44(1–2), 167–207.
Lange, M. (1999). Laws, counterfactuals, stability, and degrees of lawhood. Philosophy of Science, 66(2), 243–267.
Lewis, D. (1973). Counterfactuals and comparative possibility. In: Ifs (pp. 57–85). Springer.
Makinson, D. (1988). General theory of cumulative inference. In: M. Reinfrank, J. de Kleer, M.L. Ginsberg, E. Sandewall (Eds.), Proceedings of 2nd international workshop, non-monotonic reasoning, Grassau, FRG, June 13-15, 1988. Volume 346 of Lecture Notes in Computer Science, pp 1–18. Springer.
Marti, J., & Pinosio, R. (2014). Similarity orders from causal equations. In: European workshop on logics in artificial intelligence, pp. 500–513. Springer.
Palan, S., & Schitter, C. (2018). Prolific.ac: A subject pool for online experiments. Journal of Behavioral and Experimental Finance, 17, 22–27.
Pearl, J. (2000). Causality. Models, reasoning, and inference. Cambridge University Press.
Pearl, J. (2013). Structural counterfactuals: A brief introduction. Cognitive Science, 37, 977–85.
Schulz, K. (2011). if you wiggle A, then B will change. Causality and counterfactual conditionals. Synthese, 179(2), 239–251.
Schulz, K. (2014). Minimal models vs. logic programming: The case of counterfactual conditionals. Journal of Applied Non-Classical Logics, 24(1–2), 153–168.
Skyrms, B. (1980). The prior propensity account of subjunctive conditionals. In: Ifs (pp. 259–265). Springer
Spirtes, P., Glymour, C. N., Scheines, R., Heckerman, D., Meek, C., Cooper, G., & Richardson, T. (2000). Causation, prediction, and search. MIT Press.
Stalnaker, R. C. (1968). A theory of conditionals. In: Ifs (pp. 41–55). Springer.
Starr, W. (2019). Counterfactuals. In: Zalta, E. N. (Ed.), The stanford encyclopedia of philosophy. Fall 2019 edn. Metaphysics Research Lab, Stanford University
Starr, W. B. (2014). A uniform theory of conditionals. Journal of Philosophical Logic, 43(6), 1019–1064.
van Benthem, J. (2011). Logical dynamics of information and interaction. CUP
van Ditmarsch, H., van der Hoek, W., & Kooi, B. (2008). Dynamic epistemic logic. Springer.
Wang, Y., & Cao, Q. (2013). On axiomatizations of public announcement logic. Synthese, 190(1), 103–134.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Proofs
Proofs
Proof of Theorem 1
Soundness follows from the validity of axioms and rules. Completeness relies on Halpern (2000), which shows that MP and the axioms D0-D11 (Table 3) are sound and complete with respect to recursive causal models for a slightly different language \({\mathcal {L}}^+\). Here is a sketch of the argument.
First, formulas in the language \({\mathcal {L}}^+\) are Boolean combinations of expressions of the form \([\overrightarrow{X}{=}\overrightarrow{x}]\gamma \), with \(\overrightarrow{X} \subseteq {\mathcal {V}}\), \(x_i \in {\mathcal {R}}(X_i)\) and \(\gamma \) a Boolean combination of atoms of the form \(Y(\overrightarrow{u}){=}y\), with \(Y \in {\mathcal {V}}\), \(y \in {\mathcal {R}}(Y)\) and \(\overrightarrow{u}\) a vector of values for all variables in \({\mathcal {U}}\). An atom \(Y(\overrightarrow{u}){=}y\) is true in a model when setting variables in \({\mathcal {U}}\) to \(\overrightarrow{u}\) gives Y the value y. As mentioned, MP and axioms D0-D11 are sound and complete for recursive causal models (Theorem 3.3 in Halpern (2000)).Footnote 24 Then, note that the referred paper also mentions not only that D10 implies D2 and D9, but also that, within recursive models, D2 and D10 are equivalent. Thus, MP together with axioms D0-D8 and D11 are sound and complete for \({\mathcal {L}}^+\) within recursive models.
Now, for our purposes, observe first that axioms D0, MP, D4, D6 and D8 in the table above are identical to our axioms A0, MP, A4, A6 and A8. Moreover, axioms D1 and D2 are derivable in our system by using A8 over, respectively, A1 and A2. Then, axioms D3 and D5 are also derivable in our system, this time via propositional reasoning and \(\langle \overrightarrow{X}{=}\overrightarrow{x}\rangle \phi \leftrightarrow [\overrightarrow{X}{=}\overrightarrow{x}]\phi \), which is derivable from A7.1 and propositional reasoning.Footnote 25 Note also how D7 can be derived from A7.1, A7.2 and propositional reasoning.Footnote 26 Finally, axiom D11 is derivable in our system too (an instance of repetitive applications of A7.2). Thus, MP and axioms A0-A8 are sound and complete within recursive models for the fragment of \({\mathcal {L}}_{[\,]}\) that corresponds to \({\mathcal {L}}^+\).
To complete the argument note that, besides allowing explicit interventions on exogenous variables variables (with axioms A4 and A\(_{\mathcal {U}}\) describing the effects), the only significant way in which \({\mathcal {L}}_{[\,]}\) extends \({\mathcal {L}}^+\) is by imposing no restrictions on a counterfactual’s consequent. The extension means, effectively, that nested counterfactuals are allowed. In order to deal with them, our axiom system has axioms A7.1, A7.2 and A9: the first and the second ‘push’ intervention operators inside the counterfactual’s consequent (commuting with negations and distributing over conjunctions), and the third collapses two sequential interventions into a single one. Thus, with the help of axiom A\(_{[]}\) for the basic cases, every formula in \({\mathcal {L}}_{[\,]}\) can be translated into a semantically equivalent one in \({\mathcal {L}}^+\), for which MP and A0-A8 are sound and complete.
Proof of Proposition 1
Let \(\langle {\mathcal {S}},{\mathcal {A}} \rangle \) be a causal model. Let \(\overrightarrow{X}{=}\overrightarrow{x}\) be a counterfactual antecedent, with (i) \(\overrightarrow{X_d}\) the variables in \(\overrightarrow{X}\) whose \({\mathcal {A}}\)-value differs from the intended \(\overrightarrow{x}\), and (ii) \(\overrightarrow{Z}\) the endogenous variables not occurring in \(\overrightarrow{X}\) that are not causally dependent on variables in \(\overrightarrow{X_d}\), with \(\overrightarrow{z}\) their \({\mathcal {A}}\)-values. By construction, \(\overrightarrow{X}\) and \(\overrightarrow{Z}\) are disjoint. Now, use \({\mathcal {A}}_1\) to abbreviate \({\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}}\) (Definition 8), so \({\mathcal {A}}_1\) assigns the respective \(x_i\) to each variable \(X_i\) in \(\overrightarrow{X}\) and, for variables not in \(\overrightarrow{X}\), follows \({\mathcal {A}}\) for those not causally dependent of any variable in \(\overrightarrow{X_d}\), using \({\mathcal {S}}\) and the values already in \({\mathcal {A}}_1\) to calculate those causally dependent of some variable in \(\overrightarrow{X_d}\). Finally, let \({\mathcal {A}}_2\) be the (unique) valuation that is identical with \({\mathcal {A}}\) with respect to exogenous variables not in \(\overrightarrow{X}\), assigns to exogenous variables in \(\overrightarrow{X}\) their respective value in \(\overrightarrow{x}\), and complies with the structural functions in \({\mathcal {S}}_{(\overrightarrow{X}{=}\overrightarrow{x},\overrightarrow{Z}{=}\overrightarrow{z})}\). Take any \(Y \in {\mathcal {U}}\cup {\mathcal {V}}\); it will be shown that \({\mathcal {A}}_1(Y) = {\mathcal {A}}_2(Y)\).
First, for exogenous variables. (i) If \(Y \in {\mathcal {U}}\) is not in \(\overrightarrow{X}\), then both \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) agree with \({\mathcal {A}}\), the first because Y is not causally dependent on any other variable, and the second by definition. (ii) If \(Y \in {\mathcal {U}}\) is in \(\overrightarrow{X}\), both \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) assign to it the value indicated by \(\overrightarrow{x}\).
Now, for endogenous variables. (i) If \(Y \in {\mathcal {V}}\) is in \(\overrightarrow{X}\), then \({\mathcal {A}}_1\) gives it the value indicated by \(\overrightarrow{x}\) (by de finition), and so does \({\mathcal {A}}_2\) (by complying with \({\mathcal {S}}_{(\overrightarrow{X}{=}\overrightarrow{x},\overrightarrow{Z}{=}\overrightarrow{z})}\)). (ii) If \(Y \in {\mathcal {V}}\) is in \(\overrightarrow{Z}\) then, \({\mathcal {A}}_1\) uses the value in \({\mathcal {A}}\) (by definition), and so does \({\mathcal {A}}_2\) (via the values \(\overrightarrow{z}\), taken from \({\mathcal {A}}\)). (iii)Finally, suppose Y is neither in \(\overrightarrow{X}\) nor in \(\overrightarrow{Z}\); then, the structural functions used by \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) to calculate Y’s value are the same: from \({\mathcal {S}}\) for the first, and from \({\mathcal {S}}_{(\overrightarrow{X}{=}\overrightarrow{x},\overrightarrow{Z}{=}\overrightarrow{z})}\) for the second. On its own, this does not guarantee that Y’s value under both \(\langle {\mathcal {S}}, {\mathcal {A}}_1 \rangle \) and \(\langle {\mathcal {S}}_{(\overrightarrow{X}{=}\overrightarrow{x},\overrightarrow{Z}{=}\overrightarrow{z})}, {\mathcal {A}}_2 \rangle \) is the same: there is a unique function \(F_Y\), and yet the values of its parameters (all other variables) might be different. But, according to the previous items, the only variables in which \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) might differ are precisely the endogenous variables in neither \(\overrightarrow{X}\) nor in \(\overrightarrow{Z}\). Then, relying on the recursiveness of the model, one can use an inductive argument to show that, when the process that assigns values to variables calculates the value of such a Y, the values of all its parents will be the same in both \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\). Indeed, the step \(\#_0\) in the process assigns values to the variables in the set \(S_{0} := \{ Y \in {\mathcal {V}}\setminus (\overrightarrow{X} \cup \overrightarrow{Z}) \mid \text {the parents of } Y \text { are in } {\mathcal {U}}\cup \overrightarrow{X} \cup \overrightarrow{Z} \}\). The valuations \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) coincide in the values of the variables in \({\mathcal {U}}\cup \overrightarrow{X} \cup \overrightarrow{Z}\), so they will coincide in the values of variables in \(S_0\). Crucially, the model is recursive, so \(S_{0} \ne \emptyset \). Then, each step \(\#_{k+1}\) assigns values to the variables in the set \(S_{k+1} := \{ Y \in {\mathcal {V}}\setminus (\overrightarrow{X} \cup \overrightarrow{Z}) \mid \text {the parents of } Y \text { are in } {\mathcal {U}}\cup \overrightarrow{X} \cup \overrightarrow{Z} \cup \bigcup _{0 \le i \le k} S_i \}\). Now, \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) coincide in the values of the variables in \( {\mathcal {U}}\cup \overrightarrow{X} \cup \overrightarrow{Z} \cup \bigcup _{0 \le i \le k} S_i\), so they will coincide in the values of variables in \(S_{k+1}\). But, again, the model is recursive, so \(S_{k+1} \ne \emptyset \). Thus, eventually the values of all variables in \({\mathcal {V}}\setminus (\overrightarrow{X} \cup \overrightarrow{Z})\) will be calculated, and the values will be the same in both \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\).
Proof of Theorem 2
The proof follows the reduction axioms strategy frequently used in dynamic epistemic logicBaltag et al. (1998), van Ditmarsch et al. (2008), van Benthem (2011). In our case, the strategy relies on a sound and complete axiom system for the  -less fragment of
-less fragment of  . For the remaining formulas, those involving
. For the remaining formulas, those involving  , the strategy uses ‘reduction axioms’: valid formulas and validity-preserving rules indicating how to translate a formula with occurrences of
, the strategy uses ‘reduction axioms’: valid formulas and validity-preserving rules indicating how to translate a formula with occurrences of  into a provably equivalent one without them. Soundness follows from the validity and validity-preserving properties of the new axioms and rules (so a formula and its translation are semantically equivalent); completeness follows from the completeness of the axiom system for the
into a provably equivalent one without them. Soundness follows from the validity and validity-preserving properties of the new axioms and rules (so a formula and its translation are semantically equivalent); completeness follows from the completeness of the axiom system for the  -less fragment, as the recursion axioms define a recursive validity-preserving translation from the full
-less fragment, as the recursion axioms define a recursive validity-preserving translation from the full  into the latter. The reader is referred to Wang and Cao (2013) and (van Ditmarsch et al. 2008, Chapter 7) for a detailed explanation of this technique.
into the latter. The reader is referred to Wang and Cao (2013) and (van Ditmarsch et al. 2008, Chapter 7) for a detailed explanation of this technique.
For the underlying system, MP and axioms A0-A9, A\(_{\mathcal {U}}\) and A\(_{[]}\) constitute a sound and complete axiomatization for \({\mathcal {L}}_{[\,]}\) over causal models (Theorem 1). But, the fragment in  belonging to \({\mathcal {L}}_{[\,]}\) is not affected by the change of models (in particular, because strict interventions force the valuation to agree with the structural functions, thus always producing a causal model). Thus, as argued in Footnote 19, they also constitute a sound and complete axiom system for \({\mathcal {L}}_{[\,]}\) over general causal models.
belonging to \({\mathcal {L}}_{[\,]}\) is not affected by the change of models (in particular, because strict interventions force the valuation to agree with the structural functions, thus always producing a causal model). Thus, as argued in Footnote 19, they also constitute a sound and complete axiom system for \({\mathcal {L}}_{[\,]}\) over general causal models.
For dealing with  , axioms A10-A13 define the recursive translation that takes any formula in
, axioms A10-A13 define the recursive translation that takes any formula in  and returns a logically equivalent one without
and returns a logically equivalent one without  . Here are arguments for their validity.
. Here are arguments for their validity.
-
Axiom A10 is the basic case for the translation, as it eliminates
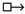 by showing how the valuation that results from a non-strict intervention is equivalent to a valuation that results from a strict intervention. Its validity follows from Proposition 1.
by showing how the valuation that results from a non-strict intervention is equivalent to a valuation that results from a strict intervention. Its validity follows from Proposition 1. -
Axioms A11 and A12 indicate how to deal with negations (commute
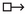 and \(\lnot \)) and conjunctions (distribute
and \(\lnot \)) and conjunctions (distribute 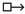 over \(\wedge \)). In particular, the validity of the former comes from the fact that a non-strict intervention is deterministic.
over \(\wedge \)). In particular, the validity of the former comes from the fact that a non-strict intervention is deterministic. -
Axiom A13 eliminates a non-strict intervention that precedes a strict one. For its validity, take a causal model \(\langle {\mathcal {S}},{\mathcal {A}} \rangle \), and note the following.
-
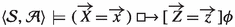 if and only if \(\langle {\mathcal {S}},{\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}} \rangle \models [\overrightarrow{Z}{=}\overrightarrow{z}]\phi \), that is, if and only if \(\langle {\mathcal {S}}_{\overrightarrow{Z} {=}\overrightarrow{z}}, ({\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}})^{{\mathcal {S}}_{\overrightarrow{Z} {=}\overrightarrow{z}}} \rangle \models \phi \).
if and only if \(\langle {\mathcal {S}},{\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}} \rangle \models [\overrightarrow{Z}{=}\overrightarrow{z}]\phi \), that is, if and only if \(\langle {\mathcal {S}}_{\overrightarrow{Z} {=}\overrightarrow{z}}, ({\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}})^{{\mathcal {S}}_{\overrightarrow{Z} {=}\overrightarrow{z}}} \rangle \models \phi \). -
\(\langle {\mathcal {S}},{\mathcal {A}} \rangle \models [\overrightarrow{X'}{=}\overrightarrow{x'}][\overrightarrow{Z}{=}\overrightarrow{z}]\phi \) with \(\overrightarrow{X'}{=}\overrightarrow{x'}\) the subassignment of \(\overrightarrow{X}{=}\overrightarrow{x}\) for \(\overrightarrow{X'}=\overrightarrow{X}\setminus {\mathcal {V}}\) if and only if \(\langle {\mathcal {S}},{\mathcal {A}} \rangle \models [\overrightarrow{X''}{=}\overrightarrow{x''}, \overrightarrow{Z}{=}\overrightarrow{z}]\phi \) with \(\overrightarrow{X''}{=}\overrightarrow{x''}\) the subassignment of \(\overrightarrow{X'}{=}\overrightarrow{x'}\) for \(\overrightarrow{X''}=\overrightarrow{X'}\setminus \overrightarrow{Z}\) (Axiom A9), that is, if and only if \(\langle {\mathcal {S}}_{\overrightarrow{X''}{=}\overrightarrow{x''}, \overrightarrow{Z}{=}\overrightarrow{z}}, {\mathcal {A}}^{{\mathcal {S}}_{\overrightarrow{X''}{=}\overrightarrow{x''}, \overrightarrow{Z}{=}\overrightarrow{z}}} \rangle \models \phi \).
Thus, it is enough to show both
$$\begin{aligned} {\mathcal {S}}_{\overrightarrow{Z} {=}\overrightarrow{z}} = {\mathcal {S}}_{\overrightarrow{X''}{=}\overrightarrow{x''}, \overrightarrow{Z}{=}\overrightarrow{z}} \qquad \text {and}\qquad ({\mathcal {A}}^{\overrightarrow{X}{=}\overrightarrow{x}})^{{\mathcal {S}}_{\overrightarrow{Z} {=}\overrightarrow{z}}} = {\mathcal {A}}^{{\mathcal {S}}_{\overrightarrow{X''}{=}\overrightarrow{x''}, \overrightarrow{Z}{=}\overrightarrow{z}}}. \end{aligned}$$with \(\overrightarrow{X''} {=}\overrightarrow{x''}\) the subassignment of \(\overrightarrow{X}{=}\overrightarrow{x}\) for \(\overrightarrow{X''}=\overrightarrow{X}\setminus ({\mathcal {V}}\cup \overrightarrow{Z})\) (thus, \(\overrightarrow{X''}\) contains only exogenous variables). The first part is straightforward, as \(\overrightarrow{X''}\) contains no endogenous variables. For the second part, it will be shown that both valuations agree in the values of every variable. Here are the cases for each exogenous variable \(U \in {\mathcal {U}}\):
-
if \(U \in \overrightarrow{Z}\), then \(U \notin \overrightarrow{X''}\) and both valuations return the appropriate value in \(\overrightarrow{z}\);
-
if \(U \notin \overrightarrow{Z}\) but \(U \in \overrightarrow{X}\), then \(U \in \overrightarrow{X''}\) and both valuations return the appropriate value in \(\overrightarrow{x}\);
-
if \(U \notin \overrightarrow{Z}\) and \(U \notin \overrightarrow{X}\), both valuations return the value \({\mathcal {A}}(U)\);
Then, here are the cases for each endogenous variable \(V \in {\mathcal {V}}\) (thus, \(V \notin \overrightarrow{X''}\)):
-
if \(V \in \overrightarrow{Z}\), then both valuations return the appropriate value in \(\overrightarrow{z}\).
-
if \(V \notin \overrightarrow{Z}\), then both valuations return the unique solution for the respective (but identical) structural equations under the (identical) values for variables in \({\mathcal {U}}\cup \overrightarrow{Z}\).
-
Rights and permissions
About this article
Cite this article
Schulz, K., Smets, S., Velázquez-Quesada, F.R. et al. Non-strict Interventionism: The Case Of Right-Nested Counterfactuals. J of Log Lang and Inf 31, 235–260 (2022). https://doi.org/10.1007/s10849-022-09358-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-022-09358-x




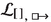 without non-strict intervention (Sect.
without non-strict intervention (Sect. 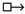 by showing how the valuation that results from a non-strict intervention is equivalent to a valuation that results from a strict intervention. Its validity follows from Proposition
by showing how the valuation that results from a non-strict intervention is equivalent to a valuation that results from a strict intervention. Its validity follows from Proposition 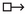 and
and 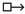 over
over 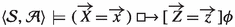 if and only if
if and only if