Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-05-14T10:42:52.827Z Has data issue: false hasContentIssue false
  • English
  • Français

CANTOR’S THEOREM MAY FAIL FOR FINITARY PARTITIONS

Part of: Set theory

Published online by Cambridge University Press:  03 April 2024

GUOZHEN SHEN Open the ORCID record for GUOZHEN SHEN [Opens in a new window]
GUOZHEN SHEN*
Affiliation:
SCHOOL OF PHILOSOPHY WUHAN UNIVERSITY NO. 299 BAYI ROAD, WUHAN, HUBEI PROVINCE 430072 PEOPLE’S REPUBLIC OF CHINA
*
E-mail: shen_guozhen@outlook.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A partition is finitary if all its members are finite. For a set A, $\mathscr {B}(A)$ denotes the set of all finitary partitions of A. It is shown consistent with $\mathsf {ZF}$ (without the axiom of choice) that there exist an infinite set A and a surjection from A onto 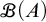$\mathscr {B}(A)$. On the other hand, we prove in $\mathsf {ZF}$ some theorems concerning 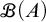$\mathscr {B}(A)$ for infinite sets A, among which are the following:

  1. (1) If there is a finitary partition of A without singleton blocks, then there are no surjections from A onto 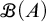$\mathscr {B}(A)$ and no finite-to-one functions from 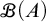$\mathscr {B}(A)$ to A.

  2. (2) For all 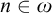$n\in \omega $, $|A^n|<|\mathscr {B}(A)|$.

  3. (3) 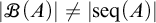$|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$, where 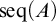$\mathrm {seq}(A)$ is the set of all finite sequences of elements of A.

Keywords

Cantor’s theoremaxiom of choicefinitary partitionpermutation model

MSC classification

Primary: 03E10: Ordinal and cardinal numbers 03E30: Axiomatics of classical set theory and its fragments
Secondary: 03E25: Axiom of choice and related propositions 03E35: Consistency and independence results
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cantor, G., Über eine elementare Frage der Mannigfaltigkeitslehre . Jahresbericht der Deutschen Mathematiker-Vereinigung , vol. 1 (1891), pp. 75–78.Google Scholar
Dawson, J. W. Jr. and Howard, P. E., Factorials of infinite cardinals . Fundamenta Mathematicae , vol. 93 (1976), pp. 185–195.CrossRefGoogle Scholar
Forster, T., Finite-to-one maps, Journal of Symbolic Logic, vol. 68 (2003), pp. 1251–1253.Google Scholar
Halbeisen, L., Combinatorial Set Theory: With a Gentle Introduction to Forcing , 2nd ed., Springer Monographs in Mathematics, Springer, Cham, 2017.CrossRefGoogle Scholar
Halbeisen, L. and Shelah, S., Consequences of arithmetic for set theory, Journal of Symbolic Logic, vol. 59 (1994), pp. 30–40.Google Scholar
Jech, T., The Axiom of Choice , Studies in Logic and the Foundations of Mathematics, 75, North-Holland, Amsterdam, 1973.Google Scholar
Lunnon, W. F., Pleasants, P. A. B., and Stephens, N. M., Arithmetic properties of bell numbers to a composite modulus I . Acta Arithmetica , vol. 39 (1979), pp. 1–16.CrossRefGoogle Scholar
Peng, Y. and Shen, G., A generalized Cantor theorem in $\mathsf{ZF}$ , Journal of Symbolic Logic, vol. 89 (2024), pp. 204–210.Google Scholar
Peng, Y., Shen, G., and Wu, L., A surjection from Cartesian square onto powerset, submitted (2023), arXiv:2207.13300.Google Scholar
Phansamdaeng, P. and Vejjajiva, P., The cardinality of the partitions of a set in the absence of the axiom of choice . Logic Journal of IGPL , vol. 31 (2023), pp. 1225–1231.CrossRefGoogle Scholar
Rota, G. C., The number of partitions of a set . American Mathematical Monthly , vol. 71 (1964), pp. 498–504.CrossRefGoogle Scholar
Shen, G., Generalizations of Cantor’s theorem in $\mathsf{ZF}$ . Mathematical Logic Quarterly , vol. 63 (2017), pp. 428–436.CrossRefGoogle Scholar
Shen, G., The power set and the set of permutations with finitely many non-fixed points of a set . Mathematical Logic Quarterly , vol. 69 (2023), pp. 40–45.CrossRefGoogle Scholar
Shen, G., On a cardinal inequality in $\mathsf{ZF}$ . Mathematical Logic Quarterly , vol. 69 (2023), pp. 417–418.CrossRefGoogle Scholar
Shen, G. and Yuan, J., Factorials of infinite cardinals in $\mathsf{ZF}$ part I: $\mathsf{ZF}$ results, Journal of Symbolic Logic, vol. 85 (2020), pp. 224–243.CrossRefGoogle Scholar
Shen, G. and Yuan, J., Factorials of infinite cardinals in $\mathsf{ZF}$ part II: Consistency results, Journal of Symbolic Logic, vol. 85 (2020), pp. 244–270.CrossRefGoogle Scholar
Sonpanow, N. and Vejjajiva, P., Factorials and the finite sequences of sets . Mathematical Logic Quarterly , vol. 65 (2019), pp. 116–120.CrossRefGoogle Scholar
Specker, E., Verallgemeinerte Kontinuumshypothese und Auswahlaxiom . Archiv der Mathematik , vol. 5 (1954), pp. 332–337.CrossRefGoogle Scholar
Tarski, A., Sur quelques théorèmes qui équivalent à l’axiome du choix . Fundamenta Mathematicae , vol. 5 (1924), pp. 147–154.CrossRefGoogle Scholar
Truss, J., The well-ordered and well-orderable subsets of a set . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik , vol. 19 (1973), pp. 211–214.CrossRefGoogle Scholar