In the beginning was information. The word came later.

Dretske (1981)

1 Epistemology

Dretske was calling for a reorientation in epistemology. He did not think that epistemologists should spend their time on little puzzles or on rehashing ancient arguments about skepticism. Rather, he held that epistemology by would be better served by studying the flow of information. I think so too. Other pioneers of this naturalistic point of view, in somewhat different ways, are Millikan (1984) and Harms (2004). Information is carried by signals. It flows through signaling networks.

2 Information

We must first ask: What is the information in a signal? The framework of signaling games, and of evolutionary or learning dynamics, will help us to answer this question. There are really two questions: What is the informational content of a signal? and What is the quantity of information in a signal? Some philosophers who have looked at Shannon’s information theory and seen that he is not trying to answer either question, have concluded that mathematical information theory is irrelevant to these concerns. I believe that this is a mistake. One need not move very far from Shannon to find the answer to the second question in the information concept of Kullback and Leibler (1951).Footnote 1 To answer the first question, a new notion of the informational content of a signal is introduced here.

The informational content of a signal consists in how the signal affects probabilities. The quantity of information in a signal is measured by how far it moves probabilities. Suppose, for instance, that there are two states, initially equiprobable. Suppose that signal A moves the probabilities to 9/10 for State 1 and 1/10 for state 2, and that signal B moves the probabilities in exactly the opposite way, 1/10 for state 1 and 9/10 for state 2. Even without knowing exactly how we are going to measure quantity of information, we know by considerations of symmetry that these two signals contain the same amount of information. They move the initial probabilities by the same amount. But they do not have the same informational content, because they move the initial probabilities in different directions. Signal A moves the probability of state 1 up; signal B moves it down. Some philosophers may balk at any use of the term information at this point. They jump to the conclusion that information theory deals only with quantity of information and is irrelevant to the question of content. Hold on, we will get to informational content.

The key to information is moving probabilities. What probabilities? We use sender–receiver signaling games of the kind introduced by Lewis (1969)Footnote 2 (and generalizations of them) as a framework allowing a precise treatment of these questions. As always, there is the question whether the framework is being correctly applied to model the situation of interest. It is assumed here that it is. We will study evolution of strategiesFootnote 3 in these games to show how adaptive dynamics can create informational content where none existed originally.

The simplest Lewis signaling games work like this: nature chooses a state from among a set of possible statesFootnote 4 with some probability. The sender observes the state and chooses a signal to send from a set of possible signals. The receiver observes the signal and chooses an act. Both sender and receiver have pure common interest; they both get paid off either one or zero according to whether the act is appropriate for the state. The possible signals have no pre-assigned meaning or content. If they are to acquire meaning it is must be as a result of the interaction of the strategies of sender and receiver.

The strategies of sender and receiver evolve over time, driven by the payoffs, according to some adaptive dynamics. One interpretation has frequencies of sender types and receiver types evolving in a large population according to evolutionary dynamics. Another has a sender and receiver learn in repeated interactions according to reinforcement learning.Footnote 5

We are interested in information not only in equilibrium, but also as interactions are still evolving. It is part of the structure of the game that the states occur with certain probabilities. The probabilities of sender and receiver strategies evolve through time. In learning dynamics these probabilities are modified by the learning rule; in evolution they are interpreted as population frequencies. At any given time, in or out of equilibrium, all these probabilities are well-defined. Taken together, they give us all the probabilities that we need to assess the content and quantity of information in a signal at that time.Footnote 6 Informational content evolves as strategies evolve.

How should we measure the quantity of information in a signal? The information in the signal about a state depends on a comparison of the probability of the state given that this signal was sent and the unconditional probability of the signal. We might as well look at the ratio:

$$ {{{\text{pr}}_{\text{sig}} \left( {\text{state}} \right)} \mathord{\left/ {\vphantom {{{\text{pr}}_{\text{sig}} \left( {\text{state}} \right)} {{\text{pr}}\left( {\text{state}} \right)}}} \right. \kern-\nulldelimiterspace} {{\text{pr}}\left( {\text{state}} \right)}} $$

where prsig is the probability conditional on getting the signal. This is a key quantity. The way that the signal changes the probability of the state is just by multiplication by this quantity.

When a signal does not change the probability of a state at all—for instance if the sender sends the same signal in all states—the ratio is equal to one, but we would like to say that the quantity of information is zero. We can achieve this by taking the logarithm to define the quantity of information as:

$$ \log \left[ {{{{\text{pr}}_{\text{sig}} \left( {\text{state}} \right)} \mathord{\left/ {\vphantom {{{\text{pr}}_{\text{sig}} \left( {\text{state}} \right)} {{\text{pr}}\left( {\text{state}} \right)}}} \right. \kern-\nulldelimiterspace} {{\text{pr}}\left( {\text{state}} \right)}}} \right] $$

This is the information in the signal in favor of that state. If we take the logarithm to the base 2, we are measuring the information in bits.

A signal carries information about many states so to get an overall measure of information in the signal we can take a weighted average, with the weights being the probabilities of the states conditional on getting the signal:

$$ {\text{I}}_{\text{states}} \left( {\text{signal}} \right) = \sum\limits_{\text{i}} {{\text{pr}}_{\text{sig}} \left( {{\text{state}}\;{\text{i}}} \right)\log \left[ {{\text{pr}}_{\text{sig}} \left( {{\text{state}}\;{\text{i}}} \right) / {\text{pr}}\left( {{\text{state}}\;{\text{i}}} \right)} \right]} $$

This is the average information about states in the signal. It sometimes called the Kullback–Leibler distance, or the information gained. This was introduced over 50 years ago, shortly after Claude Shannon published his original paper on information theory.Footnote 7 Alan Turing used almost the same concept in his work breaking the German Enigma code during World War II.Footnote 8

For example, consider the simplest Lewis signaling game. There are two states, two signals and two acts, with the states equiprobable. A signal moves the probabilities of the states, and how it moves the probability of the second state is determined by how much it moves the probability of the first, so we can plot the average information in the signal as a function of the probability of the first state given the signal, as shown in Fig. 1.

Fig. 1
figure 1

Information as a function of probability of state 1 given signal, states initially equiprobable

Full size image

If the signal does not move the probability off one-half the information is 0; if it moves the probability a little there is a little information; if it moves the probability all the way to one or to zero, the information in the signal is 1 bit. In a perfect signaling-system one signal moves the probability to one and the other moves it to zero, so each of the two signals carries 1 bit of information.

The situation is different if the states are not initially equiprobable. Suppose that state one is 6/10 and of state 2 is 4/10. Then a signal that was sent only in state two would carry more information than one that only came in state one because it would move the initial probabilities more, as shown in Fig. 2.

Fig. 2
figure 2

Information as a function of probability of state 1 given signal, states initially pr. 6, .4

Full size image

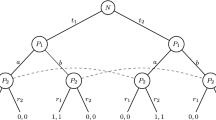
In a game with four equiprobable states a signal that gives one of the states probability one carries 2 bits of information about the state. Compare a somewhat more interesting case,Footnote 9 where nature chooses one of four states by independently flipping two fair coins. Coin 1 determines up or down—let us say—and coin 2 determines left or right. The four states, up-left etc., are equiprobable. There are now two senders. Sender 1 can only observe whether nature has chosen up or down; sender 2 observes whether it is left or right. Each sends one of two signals to the receiver.

$$ \bullet \to \bullet \leftarrow \bullet $$

The receiver chooses among four acts, one right for each state.

In an optimal signaling system equilibrium for this little signaling network, pairs of sender signals identify each of the four states with probability one—and the receiver makes the most of the information in the signals. In such a signaling system each signal carries 1 bit of information. 1 bit from each of the senders adds up to the 2 bits we had with one sender and four signals. This is a mathematical convenience of having taken the logarithms.Footnote 10

3 Information about the act

All of the information discussed so far is defined by the probabilities with which nature chooses acts and the probabilities of the sender strategies. But there is also a different kind of information in the signals. We have been discussing information about the state of nature, but there is also information about the act that will be chosen. The definitions are entirely analogous to those of information about the state.

Taken together, probabilities of the states, probabilities of sender’s strategies, and probabilities of receiver’s strategies give us unconditional probabilities of the acts. Just add up the probabilities of all combinations that give the act in question to get its initial probability. Probabilities of receiver’s strategies alone give us probability of acts given a certain signal. The information in the signal is now measured by how much the signal moves the probabilities of the acts. The average information about the act in a signal is:

$$ {\text{I}}_{\text{acts}} \left( {\text{signal}} \right) = \sum\limits_{\text{i}} {{\text{pr}}_{\text{sig}} \left( {{\text{act}}\;{\text{i}}} \right)\log \left[ {{\text{pr}}_{\text{sig}} \left( {{\text{act}}\;{\text{i}}} \right) / {\text{pr}}\left( {{\text{act}}\;{\text{i}}} \right)} \right]} $$

The definition has just the same form and rationale as the definition of information about the state. There are thus two kinds of information in a signal, and two quantities summarizing amounts of information in a signal.

The two quantities need not be the same. For instance, suppose that the sender chooses a different signal for each state but the receiver isn’t paying attention and always does the same act. Then there is plenty of information about the states in the signals, but zero information about the acts. Conversely, suppose that the sender chooses signals at random but the receiver uses the signals to discriminate between acts. Then there is zero information about the states in the signals, but there is information about the acts. There may be more states than acts or more acts than states. It is only in special cases that the two quantities of information are the same.

4 Creation of information in a signal

Let us reflect on the role of adaptive dynamics. Evolution can create information. It is not simply a question of learning to use information that is lying around, as is the case when we observe a fixed nature. With natural signs—smoke means fire—the information about states is just there, and we need to learn how to utilize it. Nature is not playing a game and does not have alternative strategies. Information about acts arrives on the scene when we learn to react appropriately to the information about states contained in the smoke. But in signaling games, there may be no initial information about acts or states in the signals. Senders and receivers may just be acting randomly. When evolution (or learning) leads to a signaling system, information is created. Symmetry-breaking shows how information can be created out of nothing. Figure 3 shows the creation of information about states by reinforcement learning.

Fig. 3
figure 3

Creation of Information ex nihilo by reinforcement learning

Full size image

In this simplest signaling game, with two equiprobable states, two signals, and two acts, it has been proved that both evolutionFootnote 11 and reinforcement learningFootnote 12 lead to perfect signaling with probability one. For now, more complex cases are investigated by simulation.

5 Informational content

Now that we know how to measure the quantity of information in a signal, let us return to informational content. This is sometimes supposed to be very problematic, but I think that it is remarkably straightforward. Quantity of information is just a summary number—1 bit, 2 bits, etc. Informational content must be a vector.Footnote 13

Consider the information in a signal about states, where there are four states. The informational content of a signal tells us how the signal affects the probabilities of each of the four states. It is a vector with four components, one for each state. Each component tells us how the probability of that state moves. So we can take the informational content of a signal to be the vector:

$$ < \log \left[ {{\text{pr}}_{\text{sig}} \left( {{\text{state}}\; 1} \right) / {\text{pr}}\left( {{\text{state}}\; 1} \right)} \right] ,\;{ \log }\left[ {{\text{pr}}_{\text{sig}} \left( {{\text{state}}\; 2} \right) / {\text{ pr}}\left( {{\text{state}}\; 2} \right)} \right], \ldots . > $$

The informational content about acts in the signal is another vector of the same form. Suppose that there are four states, initially equiprobable, and signal 2 is sent only in state 2. Then the informational content about states of signal 2 is:

$$ {\text{I}}_{\text{States}} \left( {{\text{Signal}}\; 2} \right) = \; < - \infty ,2, - \infty , - \infty > $$

The −∞ components tell you that those states end up with probability zero. The entry for state 2 tells you how much its probability has moved. If the starting probabilities had been different, this entry could have been different. For instance, if the initial probability of this state had been 1/16 with everything else the same, the information about states in signal 2 would have been:

$$ {\text{I}}_{\text{States}} \left( {{\text{Signal}}\;2} \right) = \; < - \infty ,4, - \infty , - \infty > $$

“Wait a minute,” someone is sure to say at this point. “Something very important has been left out!” What is it? “But shouldn’t the content—at least the declarative content—of a signal be a proposition? And isn’t a proposition a set of possible worlds or situations?”

Suppose a proposition is taken to be a set of states. (States can be individuated finely, and there can be lots of states if you please.) It asserts that the true state is a member of that set. A proposition can just as well be specified by giving the set of states that the true state is not in. That is what the −∞ components of the information vector do. If a signal carries propositional information, that information can be read off the informational content vector. For instance, if the signal “tells you” that it is “state 2 or state 4” in our example, then the content vector will have the form:

$$ {\text{I}}_{\text{States}} \left( {{\text{Signal}}\; 2} \right) = \; < - \infty ,\_\_, - \infty ,\_\_> $$

with the minus infinity components ruling out states 1 and 3, and the blanks being filled by numbers specifying how the probabilities of state 2 and 4 have moved.

That is to say that the familiar notion of propositional content as set of possible situations is a rather special case of the much richer information-theoretic account of content. This vector specifies more than the propositional content, and some signals will not have propositional content at all. It is the traditional account that has left something out.

6 Objective and subjective information

None of the probabilities used so far are degrees-of-belief of sender and receiver. They are objective probabilities, determined by nature and the evolutionary or learning process. Organisms (or organs) playing the role of sender and receiver need have no cognitive capacities.

But suppose that they do. Suppose that a sender and receiver are human and that they try to think rationally about the signaling game. Suppose that the sender has subjective probabilities over the receiver’s strategies and the receiver has subjective probabilities over the sender’s strategies, and that both have subjective probabilities over the states. These subjective probabilities are just degrees-of-belief; they may not be in line with the objective probabilities at all. Then each signal carries two additional kinds of subjective information. There is subjective information about how the receiver will react, which lives in the sender’s degrees-of-belief. This is of interest to a sender who wants to get a receiver to do something. There is subjective information about what state that the sender observed, which lives in the receiver’s degrees of belief. This is of interest to a receiver who wants to use the sender as a source of information about the states. Both sender and receiver use these kinds of information in decision making. Both sender and receiver strive (1) to act optimally given their subjective probabilities and (2) to learn to bring subjective probabilities in concordance with the objective probabilities in the world. They may or may not succeed. So when we are applying the account to beings that can reasonably be thought to have subjective probabilities, such as perhaps ourselves, we now have at least four types of informational content—two objective and two subjective. If the signaling game is more complex, for instance if there is an eavesdropper, the informational structure becomes richer.

7 The flow of information

In the signaling equilibrium of a Lewis Sender–Receiver game, information is transmitted from sender to receiver, but it is only in the most trivial sense that we can be said to have a flow of information. Let us consider a little signaling chain.

$$ \bullet \to \bullet \to \bullet $$

There are a sender, an intermediary, and a receiver. Nature chooses one of two states with equal probability. The sender observes the state, chooses one of two signals and sends it to the intermediary, the intermediary observes the sender’s signal, chooses one her own two signals, and sends it to the receiver. (The intermediary’s set of signals may or may not match that of the sender.) The receiver observes the intermediary’s signal and chooses one of two acts. If the act matches the state, sender, intermediary and receiver all get a payoff of one, otherwise a payoff of zero.

It is tempting to assume that these agents already have signaling for simpler sender–receiver interactions to build upon. But even if they do not, adaptive dynamics can carry them to a signaling system, as shown in Fig. 4.

Fig. 4
figure 4

Emergence of a signaling chain ex nihilo by reinforcement learning

Full size image

Although reinforcement learning succeeds in creating a signaling chain without a pre-existing signaling background, notice that it takes a much longer time than in the simpler two-agent model.

The speed with which the chain signaling system can be learned is much improved if the sender and receiver have pre-existing signaling systems. They need not even be the same signaling system. Sender and receiver can have different “languages” so that the intermediary has to act as a “translator”, or signal transducer. One could even consider an extreme case in which the sender and receiver used the same tokens as signals but with opposite meanings. For example, sender’s and receivers strategies are:

 

Sender

Receiver

State 1⇒ red

red ⇒ Act 2

State 2 ⇒ blue

blue ⇒ Act 1

A successful translator must learn to receive one signal and send another, so that the chain leads to a successful outcome.

 

Sender

Translator

Receiver

State 1 ⇒ red

see red ⇒ send blue

blue ⇒ Act 1

State 2 ⇒ blue

see blue ⇒ send red

red ⇒ Act 2

The translator’s learning problem is really quite simple, and she can learn to complete the chain very quickly.

In this signaling chain equilibrium, the sender’s signal to the translator contains one bit of information about the state and the translator’ signal to the receiver contains one bit of information about the state. And on any play, the translator’s signal to the receiver has the same informational content as the sender’s signal to her. Information flows from sender through translator to receiver. The receiver then acts just as she would have if she had observed the state directly.

What we have just illustrated in the simplest signaling chain can happen in longer chains, and more generally, in signaling networks. Information is processed by the flow of information through such networks. This is true both internally and socially. The analysis of information flow in signaling networks is a new challenge for naturalistic epistemology.