Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T23:35:38.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Computability Theory and Differential Geometry

Published online by Cambridge University Press:  15 January 2014

Robert I. Soare
Robert I. Soare*
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Illinois 60637-1546, E-mail: , soare@math.uchicago.edu, URL: http://www.cs.uchicago.edu/~soare
Get access Rights & Permissions [Opens in a new window]

Extract

Abstract. Let M be a smooth, compact manifold of dimension n ≥ 5 and sectional curvature ∣K∣ ≤ 1. Let Met(M) = Riem(M)/Diff(M) be the space of Riemannian metrics on M modulo isometries. Nabutovsky and Weinberger studied the connected components of sublevel sets (and local minima) for certain functions on Met(M) such as the diameter. 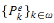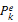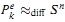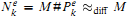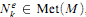They showed that for every Turing machine Te, e ϵ ω, there is a sequence (uniformly effective in e) of homology n-spheres which are also hypersurfaces, such that is diffeomorphic to the standard n-sphere Sn (denoted )iff Te halts on input k, and in this case the connected sum , so , and 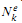is associated with a local minimum of the diameter function on Met(M) whose depth is roughly equal to the settling time ae σe(k)of Te on inputs y < k.

At their request Soare constructed a particular infinite sequence {Ai}ϵω of c.e. sets so that for all i the settling time of the associated Turing machine for Ai dominates that for Ai+1, even when the latter is composed with an arbitrary computable function. From this, Nabutovsky and Weinberger showed that the basins exhibit a “fractal” like behavior with extremely big basins, and very much smaller basins coming off them, and so on. This reveals what Nabutovsky and Weinberger describe in their paper on fractals as “the astonishing richness of the space of Riemannian metrics on a smooth manifold, up to reparametrization.” From the point of view of logic and computability, the Nabutovsky-Weinberger results are especially interesting because: (1) they use c.e. sets to prove structural complexity of the geometry and topology, not merely undecidability results as in the word problem for groups, Hilbert's Tenth Problem, or most other applications; (2) they use nontrivial information about c.e. sets, the Soare sequence {Ai}iϵω above, not merely Gödel's c.e. noncomputable set K of the 1930's; and (3) without using computability theory there is no known proof that local minima exist even for simple manifolds like the torus T5 (see §9.5).

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 10 , Issue 4 , December 2004 , pp. 457 - 486
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adjan, S. I. [1955], The algorithmic unsolvability of checking certain properties of groups, Doklady Akademii Nauk SSSR, vol. 103, pp. 533–535, (in Russian).Google Scholar
Adjan, S. I. [1958], On algorithmic problems in effectively complete classes of groups, Doklady Akademii Nauk SSSR, vol. 123, pp. 13–16, (Russian).Google Scholar
Bochnak, J., Coste, M., and Roy, M. F. [1987], Geometrie algébrique réele, Springer.Google Scholar
Boone, W. W. [1954], Certain simple unsolvable problems of group theory, Koninklijke Nederlandse Akademie van Wetenschappen. Indagationes Mathematicae, vol. 16, pp. 231–237, vol. 17 (1955), pp. 252–256, 571–577; vol. 19 (1957), pp. 22–27, 227–232.Google Scholar
Boone, W. W. [1959], The word problem, Annals of Mathematics, vol. 70, pp. 207–265.Google Scholar
Boone, W. W. [1966], Word problems and recursively enumerable degrees of unsolvability, A sequel on finitely presented groups, Annals of Mathematics, vol. 84, pp. 49–84.CrossRefGoogle Scholar
Boone, W. W., Haken, W., and Poenaru, V [1968], On recursively unsolvable problems in topology and their classification, Contributions to mathematical logic (Schmidt, H. Arnold, Schütte, K., and Thiele, H. J., editors), North-Holland, Amsterdam.Google Scholar
Britton, J. L. [1963], The word problem, Annals of Mathematics, vol. 77, pp. 16–32.Google Scholar
Chavel, I. [1993], Riemannian geometry—A modern introduction, Cambridge University Press, Cambridge.Google Scholar
Cheeger, J. [1970], Finiteness theorems for Riemannian manifolds, American Journal of Mathematics, vol. 92, pp. 61–74.Google Scholar
Church, A. [1936], An unsolvable problem of elementary number theory, American Journal of Mathematics, vol. 58, pp. 345–363.Google Scholar
Coste, M. [1982], Ensembles semi-algebriques, Geometric Algebrique Reelle et formes quadratiques, Journees S.M.F. Universite de Rennes (Colliot-Thelene, J.-L., Coste, M., Mahe, L., and Roy, M.-F., editors), Lecture Notes in Mathematics 959, Springer, pp. 109–138.Google Scholar
Csima, B. F. [2003], Computable model theory, Ph.D. thesis , The University of Chicago.Google Scholar
Csima, B. F. and Soare, R. I. [to appear], Applications of computability to differential geometry.Google Scholar
Davis, M. [1965], The undecidable, Raven Press, Hewlett, NY.Google Scholar
Davis, M. [1973], Hilbert's tenth problem is unsolvable, American Mathematical Monthly, vol. 80, pp. 233–269.Google Scholar
Dieudonné, J. [1960], Foundations of modern analysis, Academic Press, New York.Google Scholar
Carmo, M. Do [1992], Riemannian geometry, Birkhäuser, Boston, Basel, Berlin.CrossRefGoogle Scholar
Freedman, M. [1982], The topology offour-dimensional manifolds, Journal of Differential Geometry, vol. 17, pp. 357–453.Google Scholar
Gromov, M. L. [1981], Hyperbolic manifolds, groups and actions, Riemannian surfaces and related topics (Kra, I. and Maskit, B., editors), Annals of Mathematical Studies, vol. 97, Princeton University Press, Princeton, New Jersey, pp. 183–215.CrossRefGoogle Scholar
Guillemin, V. and Pollack, A. [1974], Differential topology, Prentice-Hall, Englewood Cliffs, New Jersey.Google Scholar
Haken, W. [1973], Connections between topological and group theoretical decision problems, Word problems: decision problems and the Burnside problem in group theory (Boone, W. W., Cannonito, F. B., and Lyndon, R. C., editors), Studies in Logic and the Foundations of Mathematics, vol. 71, North-Holland, Amsterdam, London, pp. 427–441.Google Scholar
Kervaire, M. and Milnor, J. [1963], Groups of homotopy spheres I, Annals of Mathematics, vol. 77, pp. 504–537.CrossRefGoogle Scholar
Levine, J. [1985], Lectures on groups of homotopy spheres, Algebraic and geometric topology, Lecture Notes in Mathematics 1126, Springer-Verlag, pp. 62–95.CrossRefGoogle Scholar
Markov, A. A. [1951], Impossibility of algorithms for recognizing some properties of associative systems, Doklady Akademii Nauk SSSR, vol. 77, pp. 953–956, (in Russian).Google Scholar
Markov, A. A. [1958], Insolubility of the problem of homeomorphy, Proceedings of the International Congress of Mathematicians (Cambridge), Cambridge University Press, pp. 300–306.Google Scholar
Massey, W. S. [1967], Algebraic topology: An introduction, Harcourt, Brace & World, Inc., New York, Chicago.Google Scholar
Miller, C. [1971], On group-theoretic decision problems and their classification, Annals of Mathematical Studies, vol. 68, Princeton University Press, Princeton, New Jersey.Google Scholar
Miller, C. [1989], Decision problems for groups—survey and reflections, Combinatorial grouptheory (Baumslag, G. and Miller, C., editors), Springer-Verlag, Heidelberg, New York, pp. 1–59.Google Scholar
Milnor, J. [1963], Morse theory, no. 51, Princeton University Press, Princeton, New Jersey.CrossRefGoogle Scholar
Milnor, J. [1965a], Lectures on the h-cobordism Theorem, Princeton University Press, Princeton, New Jersey.CrossRefGoogle Scholar
Milnor, J. [1965b], Topology from a differential viewpoint, University of Virginia Press.Google Scholar
Nabutovsky, A. [1995a], Einstein structures: Existence versus uniqueness, Geometric and Functional Analysis, vol. 5, no. 1, pp. 76–91.CrossRefGoogle Scholar
Nabutovsky, A. [1995b], Non-recursive functions, knots with “thick ropes,” and self-clenching “thick” hypersurfaces, Communications on Pure Applied Mathematics, vol. 48, pp. 381–428.CrossRefGoogle Scholar
Nabutovsky, A. [1996a], Disconnectedness of sublevel sets of some Riemannian functionals, Geometric and Functional Analysis, vol. 6, pp. 703–725.Google Scholar
Nabutovsky, A. [1996b], Fundamental group and contractible closed geodesics, Communications on Pure Applied Mathematics, vol. 49, pp. 1257–1270.Google Scholar
Nabutovsky, A. [1996c], Geometry of the space of triangulations of a compact manifold, Communications in Mathematical Physics, vol. 181, pp. 303–330.Google Scholar
Nabutovsky, A. and Weinberger, S. [1996], Algorithmic unsolvability of the triviality problem for multidimensional knots, Commentarii Mathematici Helvetici, vol. 71, pp. 426–434.CrossRefGoogle Scholar
Nabutovsky, A. and Weinberger, S. [1999], Algorithmic aspects of homeomorphism problems, Rothenberg Festschrift, Contemporary Mathematics, vol. 231, American Mathematical Society, pp. 145–250.Google Scholar
Nabutovsky, A. and Weinberger, S. [2000a], Critical points of Riemannian functionals and arithmetic groups, Publications Mathématiques. Institut de Hautes Ëtudes Scientifiques, vol. 92, pp. 5–62.Google Scholar
Nabutovsky, A. and Weinberger, S. [2000b], Variational problems for Riemannian functionals and arithmetic groups, Publications Mathématiques, Institut des Hautes Études Scientifiques, vol. 92, pp. 5–62.Google Scholar
Nabutovsky, A. and Weinberger, S. [2003], The fractal nature of Riem/Diff I, Geometrica Dedicata, vol. 101, pp. 1–54.Google Scholar
Novikov, P. S. [1955], On the algorithmic unsolvability of the word problem in groups, Trudy Matematicheskogo Instituta Imeni V. A. Steklova, 44 Izdat Akad. Nauk SSSR, Moscow, (Russian).Google Scholar
Petersen, P. [1993], Gromov-Hausdorff convergence of metric spaces, Differential geometry: Riemannian geometry (Greene, R. and Yau, S.T., editors), vol. 54, Proceedings of Symposia in Pure Mathematics, no. 3, American Mathematics Society, pp. 489–504.Google Scholar
Petersen, P. [1998], Riemannian geometry, Graduate Texts in Mathematics 171, Springer-Verlag, Heidelberg, New York.Google Scholar
Poincaré, H. [1895], Analysis situs, Journal de l'Êcole Polytechnique, Paris (2), vol. 1, pp. 1–123.Google Scholar
Rabin, M. O. [1958], Recursive unsolvability of group theoretic problems, Annals of Mathematics, vol. 67, pp. 172–194.Google Scholar
Reid, C. [1970], Hilbert, Springer-Verlag, New York, Heidelberg.Google Scholar
Rotman, J. J. [1995], An introduction to the theory of groups, Springer-Verlag, Heidelberg, New York.CrossRefGoogle Scholar
Sapir, M. V., Birget, J. C., and Rips, E. [2002], Isoperimetric and isodiametric functions of groups, Annals of Mathematics, vol. 156, pp. 467–518.Google Scholar
Smale, S. [1961], Generalized Poincare's conjecture in dimensions greater than four, Annals of Mathematics, vol. 74, pp. 391–406.Google Scholar
Soare, R. I. [1987], Recursively enumerable sets and degrees: A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg.Google Scholar
Spivak, M. [1965], Calculus on manifolds, Benjamin Press, New York.Google Scholar
Spivak, M. [1979], A comprehensive introduction to differential geometry, vol. I–V, Publish or Perish, Wilmington.Google Scholar
Stallings, J. W. [1960], Polyhedral homotopy spheres, Bulletin of the American Mathematical Society, vol. 66, pp. 485–488.Google Scholar
Turing, A. M. [1936], On computable numbers, with an application to the Entscheidungsproblem, Proceedings ofthe London Mathematical Society, vol. 42, pp. 230–265, A correction, A. M. Turing [1936], On computable numbers, with an application to the Entscheidungsproblem, Proceedings ofthe London Mathematical Society vol. 43, (1937), pp. 544–546; reprinted in Davis [1965], pp. 115–154.Google Scholar
Weinberger, S. [to appear], Computers, rigidity, and moduli: Computation and the large scale geometry of moduli spaces, Princeton University Press, (Book from Porter Lectures given at Rice University).Google Scholar