Abstract
Leslie Tharp proves three theorems concerning epistemic and metaphysical modality for conventional modal predicate logic: every truth is a priori equivalent to a necessary truth, every truth is necessarily equivalent to an a priori truth, and every truth is a priori equivalent to a contingent truth. Lloyd Humberstone has shown that these theorems also hold in the modal system Actuality Modal Logic (AML), the logic that results from the addition of the actuality operator to conventional modal logic. We show that Tharp’s theorems fail for the expressively equivalent Subjunctive Modal Logic (SML), the logic that was developed by Kai Wehmeier as an alternative to AML. We then argue that the existence of Tharp’s theorems for AML is due to a faulty interpretation of the notion of necessary truth, a feature that is not shared by SML. The paper concludes with an argument for the thesis that the existence of the distinction between truth at all worlds w and truth at all worlds w from the point of view of w as the actual world is an artifact owing to the interaction of the necessity and actuality operator.
Similar content being viewed by others
Notes
The restriction to sentences of non-modal predicate logic is lifted in Sect. 4.
Tharp’s proof of his first theorem plays on the fact that the reference of a rigid proper name can be fixed by a non-rigid description. He uses the name ‘\(\hbox {Ed}(\Phi )\)’ refer to the truth-value of \(\Phi \), stating that the truth-value of \(\Phi \) is 1, if \(\Phi \) is true, and 0, if \(\Phi \) is false. Let \(\Phi \) be true. Then, \(\Phi \) is a priori equivalent to \(\hbox {Ed}(\Phi )=1\), and ‘\(\hbox {Ed}(\Phi )=1\)’ is a necessary truth. Tharp also proves his theorems for the case where \(\Phi \) is false. For a discussion of some structural differences between theorems one and two see Humberstone (2004).
We assume a broadly Kaplanian framework in which the context supplies a unique actual world. The truth predicate applies to sentence types that are relativized to a context of utterance.
Tharp’s proof goes as follows: Let \(\Phi \) be true. \(\Phi {\leftrightarrow }(\hbox {Ed}(\Phi )=1)\) is an a priori truth, and \(\Phi \) is necessarily equivalent to \(\Phi {\leftrightarrow }(\hbox {Ed}(\Phi )=1)\).
Lewis (2002) notes that Tharp’s third theorem was obscured by some typographical mistakes and provides a cleaned up proof. We state a version of Lewis’s proof for AML.
Single quotes are used in this and related contexts as corner quotes.
Tharp’s theorems can also be read as quantifying over true contents; read this way, Theorem 1 states that for every true content C there is a true content \(C'\) such that \(C'\) is necessary and (C iff \(C'\)) is a priori. This does not seem to be the way that Tharp intends his theorems to be read, and discussion of this formulation would be beyond the scope of this paper, so we emphasize the readings in terms of which the quantification is over true sentences.
Theorem (T3S)— for every true sentence \(\Phi \), there is a true sentence \(\Phi '\) such that ‘(\(\Phi \) iff \(\Phi '\)) is a priori’ is true and ‘\(\lnot \Box \Phi \)’ and \(\lnot \Box \lnot \Phi \)” is true—fails for SML since every true subjunctively closed formula is a vacuously necessary truth.
In showing the failure of Tharp’s theorems for SML we make the relatively safe assumption that if a sentence \(\Phi \) is a priori, then \(\Phi \) is true at all worlds w from the point of view of w as actual.
Strictly speaking, we only show that no contingent truth is a priori equivalent to a genuinely necessary non-modal truth. Similar provisos are also in place for Theorems 2 and 3: the failure of Theorem 2 only shows that not every truth is necessarily equivalent to a non-modal a priori truth, and the failure of Theorem 3 only shows that not every genuinely necessary truth is a priori equivalent to a non-modal contingent truth. To remove the proviso a more general definition of necessity for SML is required, and we turn to this matter in the following section.
The requirement that \(s_{i}\) be fresh to \({\upvarphi }\), where \(s_{i}\) is fresh to \({\upvarphi }\) if for each subjunctive marker \(s_{j}\) in \({\upvarphi } \, i\ne j\), is to prevent the unintended capture of a subjunctive marker by a modal operator.
The generalized definition of vacuous necessary truth reads: \({\upvarphi }\) is a vacuously necessary truth relative to a model K if and only if \(\Box _{i}{\upvarphi }\) is true in K, where \({\upvarphi }\) is a subjunctively closed formula of SML.
The SML translation of \({ AGa}{\rightarrow }{ Ga}\) that is true in all of the same models is \({ Ga}{\rightarrow }{} { Ga}\), which is both a priori and necessary. It will not do to consider instead the SML formula \({ Ga}{\rightarrow } G^{s}a\), where the consequent is in the subjunctive mood, since this formula is not subjunctively closed, and hence not a candidate for a priori truth.
This is also true for the second theorem, as we have shown that Tharp’s second theorem holds for the notion of vacuous necessary truth but not genuine necessary truth.
References
Crossley, J. N., & Humberstone, L. (1977). The logic of ‘actually’. Reports on Mathematical Logic, 8, 11–29.
Davies, M., & Humberstone, L. (1980). Two notions of necessity. Philosophical Studies, 38, 1–30.
Evans, G. (1979). Reference and contingency. The Monist, 62, 161–189.
Humberstone, L. (2004). Two-dimensional adventures. Philosophical Studies, 118, 17–65.
Lewis, D. (2002). Tharp’s third theorem. Analysis, 62(2), 95–97.
Skyrms, B. (1989). Introduction to three theorems of metaphysics. Synthese, 81, 201–203.
Stein, J. (2013). How many notions of necessity? Philosophical Studies, 165, 605–627.
Tharp, L. (1989). Three theorems of metaphysics. Synthese, 81, 207–214.
Wehmeier, K. F. (2004). In the mood. Journal of Philosophical Logic, 33, 607–630.
Acknowledgments
A version of this paper was presented at the 2012 Actuality and Subjunctivity Workshop at the University of California, Irvine. Special thanks are extended to Kai Wehmeier, Aldo Antonelli, and Rohan French for helpful comments on earlier drafts. I would also like to thank both of the anonymous referees.
Author information
Authors and Affiliations
Corresponding author
Technical Appendix
Technical Appendix
[Kripke Structure]: A Kripke structure  is a tuple consisting of a set of worlds W, a distinguished world @ of the model we call the actual world, a domain D, and for each world w and n-ary predicate G, I(G, w) is the interpretation of G at w.
is a tuple consisting of a set of worlds W, a distinguished world @ of the model we call the actual world, a domain D, and for each world w and n-ary predicate G, I(G, w) is the interpretation of G at w.
Lemma 1
For all Kripke Structures K, world sequences \({\upomega }\), and variable assignments \({\upsigma }\),
where \(K'\) is the variant of K with the i-th world of \({\upomega }\) as the actual world.
Proof
By induction on the complexity of \({\upvarphi }\):
-
Base Case: \({\upvarphi }\) is of the form \(R(t_{1},{\ldots }, t_{n})\)
-
\(K, {\upomega } \models R^{s}_{i}(t_{1},{\ldots }, t_{n}) [{\upsigma }]\) iff
-
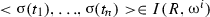 iff
iff -
\(K', {\upomega } \models R(t_{1},{\ldots }, t_{n}) [{\upsigma }]\)
-
\({\upvarphi }\) is of the form \(\lnot \Psi \)
-
\(K, {\upomega } \models \lnot \Psi ^{s}_{i} [{\upsigma }]\) iff
-
\(K, {\upomega }\) \(\nvDash \Psi ^{s}_{i} [{\upsigma }]\) iff
-
\(K',{\upomega }\) \(\nvDash \Psi [{\upsigma }]\) (by IH) iff
-
\(K', {\upomega } \models \lnot \Psi [{\upsigma }]\)
-
\({\upvarphi }\) is of the form (\(\Psi \) & \(\Phi \))
-
\(K, {\upomega } \models (\Psi ^{s}_{i }\)& \(\Phi ^{s}_{i}) [{\upsigma }]\) iff
-
\(K, {\upomega } \models \Psi ^{s}_{i } [{\upsigma }]\) and \(K, {\upomega } \models \Phi ^{s}_{i }[{\upsigma }]\) iff
-
\(K', {\upomega } \models \Psi [{\upsigma }]\) (by IH) and \(K'\), \({\upomega } \models \Phi [{\upsigma }]\) (by IH) iff
-
\(K', {\upomega } \models \) (\(\Psi \) & \(\Phi \)) [\({\upsigma }\)]
-
\({\upvarphi }\) is of the form \(\exists x\Psi \)
-
\(K, {\upomega } \models \exists x\Psi ^{s}_{i} [{\upsigma }]\) iff
-
For some x-variant assignment \({\upsigma }'\) of \({\upsigma }: K, {\upomega } \models \Psi ^{s}_{i} [{\upsigma }']\) iff
-
For some x-variant assignment \({\upsigma }'\) of \({\upsigma }: K', {\upomega } \models \Psi [{\upsigma }']\) (by IH) iff
-
\(K', {\upomega }\models \exists x\Psi [{\upsigma }]\)
-
\({\upvarphi }\) is of the form \(\Box _{j}\Psi \)
-
\(K, {\upomega } \models \Box _{j}\Psi ^{s}_{i} [{\upsigma }]\) iff
-
For all j-variants \({\upomega }_{j}\) of \({\upomega }: K, {\upomega }_{j} \models \Psi ^{s}_{i} [{\upsigma }]\) iff
-
For all j-variants \({\upomega }_{j}\) of \({\upomega }: K', {\upomega }_{j}\models \Psi [{\upsigma }]\) (by IH) iff
-
\(K', {\upomega } \models \Box _{j}\Psi [{\upsigma }]\) \(\square \)
Theorem 4
For all Kripke Structures K, world sequences \({\upomega }\), and variable assignments \({\upsigma }\),
where \({\upvarphi }^{s}_{i}\) results from \({\upvarphi }\) by subjunctivizing every indicative predicate in \({\upvarphi }\) with an index that does not already occur in \({\upvarphi }\):
Proof
-
\(K, {\upomega } \models \Box _{i}{\upvarphi }^{s}_{i} [{\upsigma }]\) iff
-
For all i-variants \({\upomega }_{i}\) of \({\upomega }: K, {\upomega }_{i} \models {\upvarphi }^{s}_{i} [{\upsigma }]\) iff
-
For all i-variants \({\upomega }_{i}\) of \({\upomega }\) and all variants \(K'\) of K with the actual world of \(K'\) the i-th world of \({\upomega }_{i}: K', {\upomega }_{i} \models {\upvarphi } [{\upsigma }]\) (by Lemma 1) iff
-
For all variants \(K'\) of \(K: K', {\upomega }\models {\upvarphi } [{\upsigma }]\)
-
\(K, {\upomega } \models \hbox {F}({\upvarphi }) [{\upsigma }]\). \(\square \)
Rights and permissions
About this article
Cite this article
Stein, J. Tharp’s theorems of metaphysics and the notion of necessary truth. Synthese 194, 1219–1231 (2017). https://doi.org/10.1007/s11229-015-0987-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0987-7




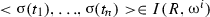 iff
iff