Optimal Control and Sensitivity Analysis of an Influenza Model with Treatment and Vaccination

Abstract

We formulate and analyze the dynamics of an influenza pandemic model with vaccination and treatment using two preventive scenarios: increase and decrease in vaccine uptake. Due to the seasonality of the influenza pandemic, the dynamics is studied in a finite time interval. We focus primarily on controlling the disease with a possible minimal cost and side effects using control theory which is therefore applied via the Pontryagin’s maximum principle, and it is observed that full treatment effort should be given while increasing vaccination at the onset of the outbreak. Next, sensitivity analysis and simulations (using the fourth order Runge-Kutta scheme) are carried out in order to determine the relative importance of different factors responsible for disease transmission and prevalence. The most sensitive parameter of the various reproductive numbers apart from the death rate is the inflow rate, while the proportion of new recruits and the vaccine efficacy are the most sensitive parameters for the endemic equilibrium point.

1 Introduction

Influenza pandemic spreads rapidly and it costs society a considerable amount in terms of health care expenses, reduction in productivity as well as loss of life. It is a yearly concern mostly during the winter season. In the history of human influenza, Spanish flu (1918–1920), caused by influenza A virus (H1N1), has resulted in the biggest influenza disaster to date. It is believed to have killed 20–100 million individuals worldwide, having a considerable impact on public health not only in the past but also in the present, as the threat of recent avian influenza epidemics is also causing widespread public concern (Murray et al. 2006). Estimates of deaths worldwide if a similar pandemic were to occur have ranged between 30 million and 384 million people. An increasing number of avian flu cases in humans, arising primarily from direct contact with poultry, in several regions of the world have prompted the urgency to develop pandemic preparedness plans worldwide. Individual countries and international organizations have developed and began to implement a strategy for forestalling (that is, containing, delaying, or minimizing the impact of) the onset of a pandemic (USGAO 2007). Influenza viruses have coexisted with humans for centuries and have historically been a cause of excessive morbidity and mortality (Cox and Subbarao 1999). WHO estimates that seasonal influenza affects about 5 to 15% of the world’s population each year, causing 3–5 million cases of severe illness worldwide including 250,000 to 500,000 deaths (Regan and Fowler 2002; USGAO 2007; World Health Organization: Influnza 2004). Because of the illness, emphasis should also be placed on treatment. Much attention has been focused on preventive strategies such as vaccination due to the high number of deaths associated with influenza, particularly among the elderly (Cox and Subbarao 1999).

Pandemic influenza poses a threat to public health at a time when the World Health Organization (WHO) has said that infectious diseases are spreading faster than at any time in history (USGAO 2007). Leading recommendations in these plans include basic public health control measures for minimizing transmission in hospitals and communities, the use of antiviral drugs and vaccination (Nunõ et al. 2006a). Vaccines are considered the first line of defense against influenza to prevent infection and control the spread of the disease (USGAO 2007). Despite the availability of preventive vaccines and public health vaccination programs, influenza inflicts substantial morbidity, mortality, and socioeconomic costs and remains a major public health problem (Alexander et al. 2004). This is largely because the protection conferred by current vaccines is dependent on the immune status of the individual, ranging between 70–90% in healthy young adults and 30–40% among the elderly and others with weakened immune systems (Alexander et al. 2004). A strategic use of such partially effective vaccines to control the spread of influenza within a certain population is of great public health interest. While annual vaccination against the influenza virus strains anticipated to be in circulation during the upcoming season is necessary to prevent new infections and subsequent epidemic outbreaks, treatment is necessary to curtail such disease outbreaks. In the event of pandemic influenza, only limited supplies of vaccine may be available (Patel et al. 2005). Effective treatment therefore will be an adequate measure in the even of an outbreak. A brief comment on previous works provides the context of this paper.

Alexander et al. (2004) explore the transmission dynamics of influenza via a mathematical model, as well as the impact of immunization with a partially effective vaccine. Their model incorporates the recruitment of infected individuals, which proves to be a crucial factor in determining the transmission dynamics of influenza. Herein, it is also shown to be the most sensitive parameter in relation to disease prevalence. Their analysis therein is based on two parts, namely; the case in which the population does not admit new infected individual, and the second does admit inflow of infective individuals. The model accounts for vaccination, with a vaccine of known efficacy, necessary to control the spread of influenza in a population. The vaccine rate is determined based on the duration of infectiousness and the rate of contact between infected and susceptible individuals leading to the infection. This information is crucial for public health implementation of influenza control measures with the aid of a partially effective vaccine. The proposed model is different from theirs as they did not consider treatment. Consequently, if the latter is ignored in the present study, we recover a simple version of their model. Of recent, Arino et al. (2008) analyze a model for influenza with vaccination and antiviral treatment. They considered treated -susceptible, -latent infective and -asymptomatic classes, derived analytic expression for the final size of the epidemic and compared their numerical computations with those of recent stochastic simulation influenza models, which have great potential for predictions of outcomes and design of control strategies. However, some of the stochastic model parameters have considerable uncertainty and are not very amenable to sensitivity analysis. Also, sensitivity and uncertainty analysis of the dependence of the control reproduction number on the parameters of the model give a comparison of the various intervention strategies. We do not carry out uncertainty analysis, but the sensitivity analysis which focuses on disease transmission and prevalence. Rwezaura et al. (2009) study a similar model to that of Arino et al. (2008) with some unique features, such as the observation that the treatment only sub-model exhibits the phenomenon of backward bifurcation which has important public health implications for disease control, since the classical requirement of having the basic reproductive number less than unity, although necessary, is no longer sufficient for disease control (Sharomi et al. 2007). There are significant differences in the content and approach in these two studies, with more detail mathematical analysis given in the latter, but, their common results agree on the point. Qiu and Feng (2009) also study a transmission dynamics model of an influenza with vaccination and antiviral treatment and noted that the benefit of antiviral use can be compromised if drug-resistant strains arise. Their model includes both drug-sensitive and resistant strains. One of the major findings is that higher levels of treatment may lead to an increase of epidemic size, and the extent to which this occurs depends on other factors such as the rates of vaccination and resistance development, which suggests that antiviral treatment should be implemented appropriately. The present study is more realistic as it includes natural recovery, which has not been previously given prominence. An economic analysis of influenza vaccination and anti-retroviral treatment for healthy working adults has been carried out by Lee et al. (2002), and it was found that vaccination in a variety of settings is cost beneficial in most influenza seasons.

Shim (2006) study epidemic models with infective immigrants (also see Brauer and van Den Driessche 2001) and vaccination, while Piccolo and Billings (2005) analyze the effect of vaccination in an immigrant SIR model. Iwami et al. (2006) propose and interpret a mathematical model of the spread of avian influenza from the bird world to the human world, where two types of outbreaks of avian influenza may occur if the humans do not prevent its spread. Their result suggests that in order to prevent the spread of avian influenza in the human world, we must take the measures not only for the birds infected with avian influenza to exterminate but also for the humans infected with mutant avian influenza to quarantine when mutant avian influenza has already occurred. Casagrandi et al. (2006) develop a simple ordinary differential equation model to study the epidemiological consequences of the drift mechanism for influenza A viruses. Improving over the classical SIR approach, they introduce a fourth class for the cross-immune individuals in the population, i.e., those that recovered after being infected by different strains of the same viral subtype in the past years. Their SIRC model predicts that the prevalence of a virus is maximum for an intermediate value of the basic reproduction number. Nishiura (2007) examine the time variations in transmission potential with regard to pandemic influenza and suggests methods to be explored to construct effective non-pharmaceutical interventions such as household quarantine and mask-wearing.

Nunõ et al. (2006a) analyze a more complex mathematical model for the evaluation of the pandemic flu preparedness plans of the United States, the United Kingdom and the Netherlands. Their results show that while the use of antiviral alone could lead to very significant reductions in the burden of a pandemic, the combination of transmission control measures, antiviral and vaccine gives the most optimal result (also see Rwezaura et al. 2009), but developing countries with limited antiviral stockpiles should emphasize their use therapeutically (due to the extra cost involved in the prophylactic measures). Motivated by this last argument, we introduce treatment in a simplified model, which captures the disease dynamics in poor settings such as rural communities in developing countries. Various studies of the flu pandemic have been carried out in recent years (Alexander et al. 2007; Casagrandi et al. 2006; Chowell et al. 2006a, b, c; Chowell et al. 2007; Nunõ et al. 2006b). Vaccination and treatment are two elements of the international strategy to forestall a pandemic, applying them concurrently have been shown to be most effective as public health measures in curtailing disease outbreak (Rwezaura et al. 2009). Such a model is more suitable for developing countries where access to medical care is difficult, only a few may get vaccinated, some may have access to treatment depending on the proximity of the health services. The combination of these strategies with non-pharmaceutical individual countermeasures which are crucial for poor resource settings, especially in developing countries (World Health Organization Writing Group 2006), provides a better way to curtail the epidemic in rural communities, where household quarantine and mask wearing could offer hope for development of these effective non-pharmaceutical interventions. Even though standard incidence may be more realistic in terms of the qualitative behavior for modeling human diseases, without loss of generality, we use the mass action incidence herein since the focus is on the numerics. Analysis (such as investigating the stability and whether the model exhibits backward bifurcation (Alexander et al. 2004; Rwezaura et al. 2009) using standard incidence has been done elsewhere (Arino et al. 2008).

The rest of this work is organized as follows: Sect. 2 is the model framework while in Sect. 3, we derive the optimality system and use the Runge-Kutta fourth order scheme to numerically simulate the treatment and vaccination efforts. Section 4 deals with the sensitivity analysis with some numerical simulations, predictive plots and plots of density distribution for some parameters. For illustrative purpose and due to the paucity of reliable data, we use two sets of parameter values, one for the optimal control (Sect. 3) and the second in Sect. 4 (for the sensitivity analysis). We note that the result would not differ if a single set of parameter values is used because these two set of values fall in the realistic ranges.

2 The Model

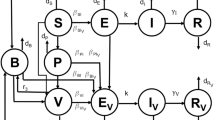
The model flow diagram of the transmission dynamics of the proposed vaccination and treatment model is depicted in Fig. 1. From the flowchart, we derive the following system of equations which captures the dynamics of influenza in a homogeneously mixing population (Table 1):

$$ \begin{aligned} S^{\prime}&=\pi\Uplambda+\omega V+\gamma R-\beta SI-(\phi+\mu)S,\\ V^{\prime}&=\phi S-\omega V-(1-\sigma)\beta VI-\mu V,\\ I^{\prime}&=(1-\pi)\Uplambda+\beta SI+(1-\sigma)\beta VI-(\mu+\kappa+\nu+\xi)I,\\ T^{\prime}&=\kappa I -[\alpha+\mu+\nu(1-\theta)]T,\\ R^{\prime}&=\alpha T+\xi I-(\gamma + \mu) R. \end{aligned} $$

(1)

with initial conditions S(0)  = S ₀, V(0)  = V ₀, I(0)  = I ₀, T(0)  = T ₀, R(0)  = R ₀ and N(t) = S(t) + V(t) + I(t) + T(t) + R(t), where N(t) is the total population at time t. The feasible set of system (1) is given by

$$ \Upomega =\left\{(S,V,I,T,R)\in {\mathbb R}^5_+: S+V+I+T+R\leq \frac{\Uplambda}{\mu}\right\}. $$

(2)

The cyclic nature of the flue pandemic requires analysis of it asymptotic dynamics, which has already been addressed using an autonomous model for which analytical and numerical methods were implemented in Rwezaura et al. (2009). Since the result of the mathematical analysis such as positivity, positively invariant feasible set (region), boundedness of solutions and stability have bee addressed in Alexander et al. (2004), Arino et al. (2008), Rwezaura et al. (2009), we avoid repetition here and only compute the reproduction numbers (when the inflow of infective immigrants π = 0) in this section, using the matrix operator method in van den Driessche and Watmough (2002). Thus, the vaccination and treatment-induced reproduction number ${\mathcal R}_{VT}$ is given by (see details in the “Appendix”).

$$ {\mathcal R}_{VT}=\frac{\beta\Uplambda(\omega+\mu+(1-\sigma)\phi)} {\mu(\phi+\omega+\mu)(\mu+\kappa+\nu+\xi)}. $$

(3)

The threshold quantity ${\mathcal R}_{VT}$ above represents the average number of infected people produced by one infected individual introduced into a naive population in the presence of vaccination and treatment. In the absence of treatment κ = 0, we have the vaccination-induced reproduction number given by

$$ {\mathcal R}_V =\frac{\beta\Uplambda(\omega+\mu+(1-\sigma)\phi)} {\mu(\phi+\omega+\mu)(\mu+\nu+\xi)}. $$

(4)

In absence of vaccination ϕ = 0 = ω = σ, we have the treatment-induced reproduction number given by

$$ {\mathcal R}_T =\frac{\beta\Uplambda}{\mu(\mu+\kappa+\nu+\xi)}. $$

(5)

In the absence of any intervention strategy (i.e., without vaccination and treatment) ϕ = 0 = ω = σ = κ, we have the basic reproduction number given by

$$ {\mathcal R}_0 =\frac{\beta\pi\Uplambda}{\mu(\mu+\nu+\xi)}. $$

(6)

Fig. 1

Model flow diagram

Table 1 Variables and parameters

3 Optimal Control Analysis

Controlling the serious threat of the influenza virus requires early preparation before the outbreak becomes overwhelming to the public sector. This virus lasts for a short period of time, mainly, during the winter season and this support the motivation to carry out the analysis on a finite time scale, which is reasonable, even though the reproduction numbers (and the asymptotic analysis, see Rwezaura et al. (2009) for details) are still important for public health purposes, since it gives an indication about the potential severity (and impact of interventions). A number of epidemiological problems have been studied using control theory (see Blayneh et al. 2009; Culshaw 2004; Fister et al. 1998; Kern et al. 2007; Lenhart and Workman 2007) to name a few, and the references therein). However, although the disease is seasonal, its cycle continues yearly; this observation calls for the importance of its asymptotic dynamics, which has been addressed in Rwezaura et al. (2009). In this section, we formulate an optimal control problem of the above influenza model in order to study the best strategies to curtail the epidemic.

For the optimal control problem, we consider the following equations

$$ S^{\prime}=\pi\Uplambda+(1-u_1)\omega V+\gamma R-\beta SI-((1+u_{2I})+\mu)S, $$

(7)

$$ V^{\prime}=(1+u_{2I})S -(1-u_1)\omega V-(1-\sigma)\beta VI-\mu V, $$

(8)

$$ I^{\prime}=(1-\pi)\Uplambda+\beta SI+(1-\sigma)\beta VI-(\mu+u_{3}+\nu+\xi )I, $$

(9)

$$ T^{\prime}=u_{3} I -\alpha T - (\mu+\nu(1-\theta))T, $$

(10)

$$ R^{\prime}=\alpha T+\xi I-(\gamma + \mu) R. $$

(11)

Equations (7)–(11) represent the dynamics for increasing vaccination, waning of vaccine and treatment rates. A analogous situation involving decreasing vaccination strategy will also be considered by using (1 − u _2D ) in the Eqs. (7) and (8).

We use the following control variables: u ₁(t) to account for controlling the rate at which vaccine wanes, u ₂(t) which measures the effectiveness of vaccination (given limited supply and a fixed (imperfect) efficacy, by the timing at which vaccine is administered, i.e., as soon and as much as possible until all supply is exhausted), and u ₃(t) to measure the effectiveness of treatment. Due do vaccine scare, we should split u ₂(t) into tow parts: u _2I for increase in vaccine uptake and u _2D for a decrease. The effectiveness of vaccination could be linked to the way it is administered, for instance, how early or late relative to the favorable season for epidemic outbreak is the vaccine given. Also, the choice of a focused (risk) group could help save the cost; there could be more to this (Bowman and Gumel 2006). The onset of therapy, that is, how early the therapy started, after a positive diagnosis, could be crucial to the effectiveness of the treatment strategy and hence to the effectiveness of drug (Ferguson et al. 2006; Linde 2001; Murray et al. 2006), and this is measured in u ₂(t) on a finite time interval [0, T] of the flu season. One question to be answered is: will there be optimal values for u ₁, u ₂(t) and u ₃(t) that improves (maximizes) the efficacy of vaccine and minimizes the cost, the side effects of the drug usage and the total number of infected population within a given community subject to emigration?

The control problem involves a model in which the number of individuals with flu and the cost of applying controls on waning, vaccination, and treatment rates u ₁(t), u ₂(t) (u ₂(t) = u _2I or u _2D ) and u ₃(t), respectively, are minimized subject to the differential Eqs. (7)–(11). u ₂(t) = u _2I or u _2D denote respectively the increase and decrease in vaccination rate. Generally, due to the perceived gain in vaccination, the coverage might increase while in some instances, when the payoff to vaccinate is not high, then, individuals may refrain from taking the shot and thus a decrease in vaccine uptake is observed. Consequently, it is therefore important to consider these two scenarios. Our objective functional is defined as

$$ J= \min_{u_1,u_2,u_3} \int\limits_0^{t_f}\left[ A_1I + C_1u_1^2 + C_2u_2^2 + C_3u_3^3 \right]dt + A_2S(t_f) - A_3V(t_f), $$

(12)

where t _f is the final time and the coefficients, A ₁, C ₁, C ₂, C ₃ are balancing cost factors. This performance specification involves minimizing the number of individuals with flu, as well as the costs for applying controls on vaccine waning rate (u ₁(t)), vaccination (u ₂(t)) and treatment (u ₃(t)), in individuals with flu. The costs can include funds needed for control implementation, hospitalization and lost of many hours of work due to illness. More often the cost of implementing a control would be nonlinear. In this paper, a quadratic function is implemented for measuring the control cost (Blayneh et al. 2009; Caetano and Yoneyama 2001; Felippe De Souza et al. 2000; Joshi 2002; Karrakchou et al. 2006; Kirschner et al. 1997; Lenhart and Bhat 1992; Lenhart and Yong 1997; Yan et al. 2007; Yan and Zou 2008). Furthermore, A ₂ S(t _f ), A ₃ V(t _f ) are respectively the fitness of the susceptible and the vaccinated group at the end of the process as a result of a reduction in the rate at which vaccine wanes, vaccinated and treatment efforts are implemented. Hence, using the result of Lukes (1982) an optimal control, $u^*_1(t), u_2^*(t)$ and $u^*_3(t),$ exists such that

$$ J(u^*_1(t), u_2^*(t),u^*_3(t))=\min\{J(u_1(t),u_2(t),u_3(t))|u_1(t),u_2(t),u_3(t)\in{\mathcal{U}}\}, $$

(13)

where ${\mathcal{U}}=\{(u_1(t),u_2(t),u_3(t)) | (u_1(t),u_2(t),u_3(t)) \hbox{ measurable, } a_i\leq (u_1(t),u_2(t),u_3(t))\leq b_i,\,\,i=1,2,3,\quad a_i = 0, b_i=1\,\,t\in[0,t_f]\}$ is the control set.

The necessary conditions that an optimal control must satisfy come from the Pontryagin’s Maximum Principle (Pontryagin et al. 1986). This principle converts (7)–(11) and (12) into a problem of minimizing pointwise a Hamiltonian H, with respect to (u ₁(t), u _2I (t), u ₃(t)). First we formulate the Hamiltonian from the cost functional (12) and the governing dynamics (7)–(11) to obtain the optimality conditions.

$$ \begin{aligned} H&= A_1I + C_1u_1^2 + C_2u_{2I}^2 + C_3u_3^2 + \lambda_{S}\left(\pi\Uplambda+(1-u_1)\omega V+\gamma R-\beta SI-((1+u_{2I})+\mu)S \right)\\ &+ \lambda_{V} \left((1+u_{2I}) S-(1-u_1)\omega V-(1-\sigma)\beta VI-\mu V \right)\\ &+ \lambda_{I}\left( (1-\pi)\Uplambda+\beta SI+(1-\sigma)\beta VI-(\mu+u_{3}+\nu+\xi )I\right)\\ &+ \lambda_{T}\left( u_{3} I -\alpha T - (\mu+\nu(1-\theta))T\right)\\ &+ \lambda_{R}\left( \alpha T+\xi I-(\gamma + \mu) R \right) \end{aligned} $$

(14)

where the λ _S , λ _V , λ _I , λ _T , λ _R are the associated adjoints for the states S, V, I, T, R. The system of equations is found by taking the appropriate partial derivatives of the Hamiltonian (14) with respect to the associated state variable.

Theorem 1

Given optimal control$u^*_1,u^*_{2I},u^*_3$and solutionsS^*, V^*, I^*, T^*, R^*of the corresponding state system (7)–(11) that minimizesJ(u₁, u_2I , u₃) over${\mathcal{U}},$there exist adjoint variables λ _S , λ _V , λ _I , λ _T , λ _R satisfying

$$ - \frac{d\lambda_i}{dt}=\frac{\partial H}{\partial i}, $$

(15)

with transversality conditions

$$ \lambda_S(t_{f}) = A_2,\quad \lambda_V(t_{f}) = - A_3,\quad \lambda_i(t_{f})=0, \quad {\rm where} \,\, i=I,T,R, $$

(16)

$$ \begin{aligned} u^*_1 & = {\min}\left\{b_1,\max\left[a_1, \, {\frac{\omega V(\lambda_S -\lambda_V)}{2C_1}}\right]\right\},\\ u_{2I}^* &= \min \left\{b_2,\max \left[a_2,\, {\frac{S(\lambda_S -\lambda_V)}{2C_2}}\right]\right\}\\ & \hbox{and,}\\ u^*_3 & = \min\left\{b_3,\max\left[a_3,{\frac{I(\lambda_I -\lambda_T )}{2C_3}}\right]\right\} .\\ \end{aligned} $$

(17)

Proof

Corollary 4.1 of Flemin and Reshel (1975) gives the existence of an optimal control pair due to the convexity of the integrand of J with respect to u ₁, u _2I and u ₃, a priori boundedness of the state solutions, and the Lipschitz property of the state system with respect to the state variables. The differential equations governing the adjoint variables are obtained by differentiating the Hamiltonian function and evaluating at the optimal control pair. Then, the adjoint system can be written as,

$$ \begin{aligned} -\frac{d\lambda_{S}}{dt}&= \frac{\partial H}{\partial S}, \quad \lambda_{S}(t_f) = A_2, \\ \frac{d\lambda_{V}}{dt} &= \frac{\partial H}{\partial {V}}, \quad \lambda_{V}(t_f) = -A_3, \\ & \cdots \\ -\frac{d\lambda_{R}}{dt}&= \frac{\partial H}{\partial R}, \quad \lambda_{R}(t_f)=0, \end{aligned} $$

evaluated at the optimal control pair and corresponding states, which result in the stated adjoint system (15) and (16). By considering the optimality conditions,

$$ 0=\frac{\partial H}{\partial u_1}, \quad 0=\frac{\partial H}{\partial u_{2I}} \quad \hbox{ and }\quad 0=\frac{\partial H}{\partial u_3}. $$

Solving for $u_1^*, u_{2I}^*$ and $u_3^*$ subject to the constraints, the characterization (17) can be derived and we have

$$ \begin{aligned} 0=\frac{\partial H}{\partial u_1}&=2C_1u_1^* - \omega V(\lambda_S - \lambda_V ),\\ 0=\frac{\partial H}{\partial u_{2I}} &= 2C_2u_{2I}^* - S(\lambda_V - \lambda_S ),\\ 0=\frac{\partial H}{\partial u_3} &= 2C_2u_3^* - I( \lambda_I - \lambda_T ). \end{aligned} $$

(18)

Hence, we obtain (see Lenhart and Workman 2007)

$$ u^*_1 = \frac{\omega V(\lambda_S -\lambda_V )}{2C_1 },\quad u^*_{2I} = \frac{S(\lambda_V -\lambda_S )}{2C_2}, \quad u^*_3 = \frac{I(\lambda_I -\lambda_T )}{2C_3}. $$

(19)

Then, by standard control arguments involving the bounds on the controls, we conclude for control u ₁:

$$ u_1^*= \left\{\begin{array}{ll} a_1 & \quad \frac{\omega V(\lambda_S -\lambda_V )}{2C_1}\leq a_1,\\ \frac{\omega V(\lambda_S -\lambda_V )}{2C_1} & \quad a_1<\frac{\omega V(\lambda_S -\lambda_V )}{2C_1} < b_1,\\ b_1&\quad \frac{\omega V(\lambda_S -\lambda_V )}{2C_1} \geq b_1. \end{array} \right. $$

(20)

In compact form

$$ u^*_1 = \min \left\{1, \frac{\omega V(\lambda_S -\lambda_V )}{2C_1}\right\}, $$

(21)

Similarly, for u _2I and u ₃ in compact form, we have

$$ u_{2I}^*=\min \left\{1, \frac{S(\lambda_S -\lambda_V )}{2C_2} \right\}, \quad u_3^*=\min \left\{1, \frac{I(\lambda_I -\lambda_T )}{2C_3}\right\}. $$

□

For the case involving decreasing vaccination rate, we give the following theorem

Theorem 2

Given optimal control$u^*_1,u^*_{2D},u^*_3$and solutions$S^*,V^*,I^*,T^*,R^*$of the state system corresponding to decreasing vaccination rate that minimizesJ(u₁, u_2D , u₃) over${\mathcal{U}},$there exist adjoint variables λ _S , λ _V , λ _I , λ _T , λ _R satisfying

$$ - \frac{d\lambda_i}{dt} =\frac{\partial H}{\partial i} $$

(22)

together with the transversality conditions

$$ \lambda_S(t_{f}) = A_2, \lambda_V(t_{f}) = - A_3, \lambda_i(t_{f})=0, \,\, {\rm where} \,\, i=I,T,R $$

(23)

$$ \begin{aligned} u^*_1 & = {\rm min}\left\{b_1,{\rm max} \left[a_1, \frac{\omega V(\lambda_S -\lambda_V ) }{2C_1}\right]\right\}, \quad u^*_{2D} = {\rm min}\left\{b_2,{\rm max}\left[a_2, \frac{S(\lambda_V -\lambda_S )}{2C_2}\right]\right\},\\ & \hbox{and}\\ u_3^* & = {\rm min}\left\{b_3,{\rm max}\left[a_3, \frac{I(\lambda_I -\lambda_T )}{2C_3}\right]\right\}. \end{aligned} $$

(24)

Table 2 Parameters values used in the optimal control simulation (7)–(11)

Next, we discuss the numerical solutions of the optimality system and the corresponding results of varying the optimal controls u ₁, u _2I , u _2D and u ₃, some parameter choices, and the interpretations from various cases using the baseline parameter values given in Table 2. Due to lack of data, most of the parameter values are assumed within realistic ranges for a typical scenario in a rural community for the purpose of illustration. The units where applicable are per days.

3.1 Numerical Illustrations

Numerical solutions to the optimality system comprising of the state Eqs. (7)–(11) and adjoint Eq. (15) are carried out using MatLab and using parameters in Table 2 together with the following weight factors and initial conditions: A ₁ = 90, A ₂ = 100, A ₃ = 6,000, C ₁ = 130, C ₂ = 110, C ₃ = 130, S(0) = 1, 000, V(0) = 500, I(0) = 0, T(0) = 0, R(0) = 0. The algorithm is the forward-backward scheme; starting with an initial guess for the optimal controls u ₁, u ₂ and u ₃, the state variables are then solved forward in time from the dynamics (7)–(11) using a Runge-Kutta method of the fourth order. Then, those state variables and initial guess for u ₁, u ₂ and u ₃ are used to solve the adjoint Eq. (15) backward in time with given final conditions (17), again employing a fourth order Runge-Kutta method. The controls u ₁, u ₂ and u ₃ are updated and used to solve the state and then the adjoint system. This iterative process terminates when current state, adjoint, and control values converge sufficiently (Agusto 2009a, 2009b; Blayneh et al. 2009; Jung et al. 2002; Kwon 2006; Lenhart and Workman 2007).

For the figures presented here, we assume that the weight factors C ₁ and C ₃ associated with controls u ₁ and u ₃ are greater than C ₂ which is associated with control u _2I and u _2D . This assumption is based on the facts that the cost associated with u ₁ and u ₃ will include the cost of treatment and hospitalization, and the cost associated with u _2I or u _2D will include the cost of administration of vaccine.

The numerical results are obtained for different values of β, while keeping the remaining parameters unchanged in each simulation. At first, the three optimal control functions u ₁, u _2I and u ₃ for controlling vaccine waning, increased vaccination and treatment, are obtained respectively. These optimal control functions are designed in such a way that they minimize the cost function given by (12). An increased contact rate (β) is an indication that vaccine waning rate, increased vaccination and treatment efforts have lower efficacy. Therefore, in this case, to optimize (minimize) the number of infectious individuals, one has to give treatment and vaccination at the onset of the out-break. We note that the shape of the figures for u _2I and u ₃ with u ₁ = 1 when β = 0.04215 and 0.01025, respectively is the same as that in Fig. 2a. Also, when u ₃ = 0 the shape of u ₁ and u _2I with β = 0.0425 as well as that of u ₃, u _2I when u ₁ = 1 but β = 0.04215 and 0.01025, respectively, does not differ much from that from Fig. 2b (since it will take a while before an active control program can be implemented, we conclude that Fig. 2b provides an acceptable estimate of the control terms. Other figures are not shown to avoid repetition). Thus, after setting u ₃ = 0 (no treatment), we searched for optimal control functions for the vaccine waning rate, u ₁, and increased vaccination, u _2I : We repeat this process to search for optimal treatment control function, u ₃, and optimal increased vaccination control function, u _2I , while setting u ₁ = 1 (no control on the vaccine waning rate)

Fig. 2

Graphical representation of the control functions for increase in vaccine uptake using β = 0.01025 and β = 0.04215

3.2 Discussion

Only the simulations for the vaccinated, infected and treated classes, except in Fig. 3 are shown. From Fig. 3, if we have to use one control in addition to increasing vaccination, then, treatment is more effective than the vaccine waning rate in reducing the size of infectious individuals. This highlights the effectiveness of treatment measures in controlling the diseases. In perspective, one could conclude from the controls in Fig. 2 that full treatment should be given while increasing vaccination at the onset of the disease, with vaccine waning rate kept small in the middle of the time interval when control efforts are put in placed. This means that treatment is more important in the beginning of disease outbreak. On the other hand, prevention is more important while the disease prevails.

Fig. 3

Simulations of the influenza model (7)–(11) for increasing vaccination using β = 0.01025

As it is depicted in Figs. 3 and 4, the infectious population levels obtained using the three controls (vaccine waning rate, increased vaccination and treatment) with increased vaccination are lower than their counter part which result from reducing the vaccine waning rate with increased vaccination. We conclude from this that: intervention practices which involve the vaccine waning rate, increased vaccination and treatment controls yield a relatively better result. Another notable feature of these figures is that when the average contact rate (β) is increased (preventive control has poor efficacy), then a combined control effort yields a result that is not remarkably different from those obtained using only one of the controls.

Fig. 4

Simulations of the V, I, T-classes for increasing vaccination using β = 0.04215

Using decreased vaccination control strategy, Fig. 5, shows that using the three forms of control strategy at the beginning of the disease outbreak is effective in minimizing the population of infectives. Thus, this control strategy with decreased vaccination is not effective as the disease advances. Also, comparing the effectiveness of the two vaccination strategies (not shown here) reveals that increasing vaccination efforts is more effective than decreasing vaccination at all stages of the disease. Although, a decreased vaccination strategy may be practiced at the beginning of the disease, while a full increased vaccination strategy be implemented as the disease advances. Nonetheless, treatment seems to do well in the presence of increased vaccination.

Fig. 5

Simulations of the V, I, T-classes for decreasing vaccination using β = 0.01025

4 Sensitivity Analysis

Sensitivity analysis and simulations are important to determine how best we can reduce the effect of influenza, by studying the relative importance of different factors responsible for its transmission and prevalence. Generally speaking, initial disease transmission is directly related to the basic reproduction number, and the disease prevalence is directly related to the endemic equilibrium point E ^* (Chitnis et al. 2008), specifically to the magnitude of I ^*. We calculate the sensitivity indices of the reproduction numbers ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T, {\mathcal R}_0,$ and the endemic equilibrium point E ^* to the parameters in the model. The sensitivity of E ^* was not considered in Rwezaura et al. (2009). The parameter values used in this section are shown in Table 3, chosen from the realistic ranges for illustrative purpose.

Table 3 Parameter values used in this section

4.1 Sensitivity Analysis of ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T,$ and ${\mathcal R}_0$

Since we have the explicit expressions for ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T,$ and ${\mathcal R}_0,$ we can derive an analytical expression for its sensitivity to each parameter using the normalized forward sensitivity index as described by Chitnis et al. (2008). The sensitivity indices of ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T,$ and ${\mathcal R}_0$ with respect to the parameters $\Uplambda,$ and β equals 1.0, and does not depend on any parameter value. Table 4 shows the sensitivity indices of ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T,$ and ${\mathcal R}_0$ with respect to each of the thirteen parameters used in the model. The most sensitive parameter to all the reproductive numbers is the natural death rate μ followed by $\Uplambda,\beta$ and σ. The least sensitive parameter was ν for ${\mathcal R}_{VT}, {\mathcal R}_T$ and ${\mathcal R}_0$ while for ${\mathcal R}_V$ the least sensitive parameter was ω. The negative sign of the sensitivity indices for ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T,$ and ${\mathcal R}_0$ implies that increase in the relevant parameter leads to the decrease in the corresponding reproductive number. Figure 6a is the graphical representation of ${\mathcal R}_{VT}$ against the vaccine efficacy σ = 0.00, 0, 25, 0.5, 0.75, 1. ${\mathcal R}_{VT}$ increases with decreasing σ. Figure 6b shows the plot of the reproductive numbers against the effective contact rate β for β ∈ [0 1]. It can be seen from the plots that as β increases ${\mathcal R}_0$ increases faster than the others followed by ${\mathcal R}_T, {\mathcal R}_V,$ and ${\mathcal R}_{VT}.$ This reveals the importance of vaccination and treatment, a result which agrees with that in Rwezaura et al. (2009). Consequently, this scenario for rural and developing settings will imply that they should focus more on prevention, as vaccination seems to do better than treatment with the same set of parameter values. Vaccination may also mean either an inoculation which reduces susceptibility to infection or an education program (Brauer 2004) such as encouragement of better hygiene, social distancing or mask-wearing, even though it reaches only a fraction of the susceptible population (whence its imperfect nature). In resource rich countries, the use of antiviral alone which is readily available could lead to very significant reductions in the burden of an epidemic (Nunõ et al. 2006a), but developing countries in general have limited antiviral stockpiles. Therefore, a massive educational campaign should be put in place in the developing world as the first strategy in their preparedness plan.

Table 4 Sensitivity indices of ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T,$ and ${\mathcal R}_0$

Fig. 6

Plot of ${\mathcal R}_{VT}$ against the effective contact rate β = [0 1] (a) by changing the vaccine efficacy σ for σ = 0.00, 0, 25, 0.5, 0.75, 1. (b) Plot of ${\mathcal R}_{VT}, {\mathcal R}_V, {\mathcal R}_T, {\mathcal R}_0$ against the effective contact rate β = [0 1]

4.2 Sensitivity Analysis of the Endemic Equilibrium

Since we do not have explicit expression of E ^*, the endemic equilibrium point, analytical derivation of sensitivity indices is a daunting task. We therefore compute the sensitivity index numerically using the method described by Chitnis et al. (2008). This method requires the endemic equilibrium point to be known. Using numerical methods, the endemic equilibrium point for the model using parameter values in Table 3 is

$$ E^*=(7.7938,8.1976,0.3534,0.1514,0.3739). $$

Table 5 shows the sensitivity indices for the endemic equilibrium with respect to each parameter. The most sensitive parameter for state variable I ^* is π followed σ, then $\Uplambda, \mu,$ and β. The intuitive explanations of the sensitivity indices of the endemic equilibrium point is that, increase in disease prevalence will lead to decrease in the equilibrium of human population because of the disease-induced death rate ν, and decrease in disease prevalence will lead to an increase in the equilibrium of humans because the disease-induced death rate will be reduced. These intuitive explanations agree with the signs of the sensitivity indices of the endemic equilibrium with respect to most of the model parameters (Table 5).

Table 5 Sensitivity indices of the endemic equilibrium

4.3 Numerical Simulations

To explore the dynamical behavior of influenza and illustrate some analytical results, numerous numerical simulations are carried out using the parameter values in Table 3. These includes the time series plots for the model system, parameters estimation and predictive plots using Markov Chain Monte Carlo methods.

4.3.1 Time Series Plots

The time series plots illustrates the variation of the number of individuals in each compartment of the population with respect to time (in years). Figure 7 shows the time series plot for the influenza model. The initial values used for the simulations are S ₀ = 1,000; V ₀ = 500; I ₀ = 0; T ₀ = 0; R ₀ = 0. From the plot, we see that the disease tends to die down as it approaches the disease-free equilibrium E ⁰  = (9.6774, 10.3226, 0.0, 0.0, 0.0), due to the combined effects of treatment and vaccination.

Fig. 7

Time series plot for the influenza model

4.3.2 Parameter Estimation and Predictive Plots

We first generate random samples using normal distribution and fit the data using least squares estimate (see Table 6) for the model parameter values given in Table 3. Figure 8 shows the plot of the generated samples and the fitted data against time. Although the model fit the data well, we are yet uncertain to what extent these parameters are correct. We therefore employ a parameter estimation process using MCMC methods. For a better location of the posterior distribution, we perform 1,000 initial runs using the model parameter values and the results are used as prior distribution to re-run the model with 10,000 simulations. The chain plots reveals the convergence of the chain and we can use the results for estimation and predictive inference. Table 7 shows the prior distribution (Prior), mean posterior distribution (Post-mean), the posterior standard deviation (std), the Markov Chain error (MC-err), and the convergence of each parameter after 10,000 simulations. Figure 9 shows the chain plot of each parameter and Fig. 10 shows the density distribution of each parameter. From Figs. 9 and 10, it can be seen that the graphs of ϕ, ω, θ and ν are not normally distributed. This is due to the presence of correlation between ϕ and ω, and θ and ν. Figure 11 shows the correlation between pairs of parameters for ten parameters excluding $\Uplambda,\pi,$ and μ. It can be seen that there is a positive correlation between ϕ and ω, and between θ and ν. Figure 12 depicts the predictive envelope of the model fit with the squares corresponding to 90–99% posterior region. The y[i]’s, for i = 1,…, 5 represent the S, V, I, T and R classes, respectively.

Table 6 Fitted parameters from least square estimate using fminsearch

Fig. 8

Time series plot for the fit using least squares estimates

Table 7 MCMC statistics for nsimu = 10,000

Fig. 9

Plot of chain for some parameters

Fig. 10

Plot of density distribution for some parameters

Fig. 11

Plot of chain parameters in pair for some parameters

Fig. 12

Prediction plot for the model

4.4 Discussion

Sensitivity analysis of the reproductive numbers and the endemic equilibrium (EE) are carried out numerically to determine the relative importance of each parameter to the disease transmission and prevalence. The sensitivity results of the reproductive numbers shows that μ is most sensitive parameter (followed by $\Uplambda,\beta,\sigma$ in that order) compared to other parameters, and the disease induced-death rate ν was the least sensitive parameter. The sensitivity results for the EE shows that π was the most sensitive parameter for I ^* followed by σ, then $\Uplambda,\mu,$ and β. Since the reproductive numbers measure the initial disease transmission, and E ^* is a measure of disease prevalence, it is necessary to think of strategies to reduce the various reproductive numbers and E ^*. Since μ is the most sensitive parameter for the initial transmission, it is insensitive to reduce the disease transmission by allowing more individuals to die, hence strategies to reduce the initial disease transmission while keeping the natural death rate at a minimum should be employed. The analysis therefore suggests some control measures such as vaccination and treatment strategies to reduce the initial disease transmission and prevalence. We note here that the sensitivity analysis is quite robust because it certainly agrees with results using latin hypercube sampling (see Fig. 8). Numerical simulations of the model and MCMC runs are performed. Using the original parameters and the posterior mean distribution parameters, the value of the reproductive numbers were computed as shown in Table 8. Since they are all greater than 1, this indicate that the disease is persistent in the community/population. This calls for attention from health personnel and the society to work out further necessary control procedures to curtail the disease. We also study the predictive posterior distribution of the model fit for a randomly selected subset of the chain and calculate the predictive envelope of the model.

Table 8 Reproductive numbers for original and posterior mean distribution parameters

5 Conclusion

The construction of a mathematical model of a complex physical/biological situation involves a certain amount of simplifications. This is because the purpose of the model is the description and prediction of the essential patterns of the process and not the achievement of its complete analysis. This paper presents a detailed mathematical analysis of an ODE model representing influenza transmission dynamics under various scenario’s of intervention measures. We use a variety of mathematical techniques including Optimal control, Hamiltonian, numerical simulations, sensitivity analysis and MCMC to analyze the model. Influenza virus is seasonal with visible outbreak during the winter season, with children, elderly and those with weakened immune system being the most susceptible (Cox and Subbarao 1999; World Health Organization Writing Group 2006). The study presented herein is not exhaustive and can be extended in various ways to include:- time delay before vaccine provides protective immunity—age-structure model to account for the most vulnerable age groups—dynamics of co-infection with other diseases (accounting for weakened immunity due to other infections). A more detail study of the effects of seasonal variation (with the degree of seasonality) and climate change are also of interest. We do not include seasonal forcing in the baseline model since there are little data that can be used to estimate country-specific estimates of seasonal forcing amplitudes (Bauch et al. 2009). However, it is observed that including seasonal contact of the form $\beta(t)=\beta+\beta\sin(2\pi t/365),$ damping oscillations occur in Fig. 7. Thus, the short term impact of seasonal forcing on model outcomes is worth an exploration. Nevertheless, the damping comes from the fact that seasonal forcing has relatively little impact on total number of cases over a long time horizon, regardless of the amplitude of forcing (the degree of seasonality may remove the oscillations). This occurs because disease incidence over long periods of time is controlled primarily by other factors such as birth rate and population density, whereas seasonality functions primarily dictate the distribution and timing of epidemic outbreaks on timescales of less than a decade (Bauch and Earn 2003). If β = β(t), the system becomes non-autonomous and the analysis is more challenging. An important feature of influenza is that individuals in the exposed (or latent) class can transmit infection, and this has not been accounted for in this study. Further, it is crucially important that antivirals are administered within a 48-h window; otherwise, the treatment will be ineffective. Thus a model which accounts for the time at which treatment is administered could be worthwhile.

Also, those vaccinated might have less severe symptoms (due to effectiveness of the vaccine, as opposed to the efficacy of vaccine σ which prevents infection) and hence result in less chance of disease-induced death. This can be included into the model by addition of one more class of infected vaccinated I _V , say. Herein, the effectiveness of vaccine was neglected by assuming that small a proportion of vaccination means minor effect on mortality.

Finally, our analysis assumes that control can be implemented very fast, which may somehow be unrealistic because in most situations, it will take a while before an active control program can be implemented, even on a small population like a school or a hospital, and even when preparations were made before introduction of the infection. However, this may be an interesting point to investigate in a future study.

Appendix

1.1 Computation of the Reproduction Numbers ${\mathcal R}_{VT}$

These are the epidemic threshold numbers necessary for community-wide control of the disease. From system 1 we have,

$$ \frac{d}{dt} \left[\begin{array}{c} I \\ T \\ R \end{array}\right] = F_i(x)-V_i(x) = \left[\begin{array}{c} \beta SI + (1-\sigma)\beta VI\\ 0 \\ 0 \end{array} \right] - \left[\begin{array}{c} -(1-\pi)\Uplambda+(\mu+\kappa+\nu+\xi)I \\ -\kappa I +[\alpha+\mu+\nu(1-\theta)]T \\ -\alpha T-\xi I+(\gamma + \mu) R \end{array} \right] $$

(A-1)

The corresponding Jacobian matrices are given by

$$ F=\left[\frac{\partial F_i(x)}{\partial x_j} \right] =\left[\begin{array}{ccc} \beta S + (1-\sigma)\beta V & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] $$

(A-2)

and

$$ V=\left[\frac{\partial V_i(x)}{\partial x_j}\\ \right]=\left[\begin{array}{ccc} \mu+\kappa+\nu+\xi & 0 & 0 \\ -\kappa & \alpha+\mu+\nu(1-\theta) & 0 \\ -\xi & -\alpha & \gamma+\mu \end{array} \right] $$

(A-3)

with

$$ V^{-1}=\left[\begin{array}{ccc} \frac{1}{\mu+\kappa+\nu+\xi} & 0 & 0 \\ \frac{\kappa}{(\mu+\kappa+\nu+\xi)(\alpha+\mu+\nu(1-\theta))} & \frac{1}{\alpha+\mu+\nu(1-\theta)} & 0 \\ \frac{\kappa\alpha+\xi(\alpha+\mu+\nu(1-\theta))} {(\mu+\kappa+\nu+\xi)(\alpha+\mu+\nu(1-\theta))(\gamma+\mu)} & \frac{\alpha}{(\alpha+\mu+\nu(1-\theta))(\gamma+\mu)} & \frac{1}{\gamma+\mu} \end{array}\right] $$

(A-4)

$$ FV^{-1}=\left[\begin{array}{ccc} \frac{\beta S + (1-\sigma)\beta V}{\mu+\kappa+\nu+\xi} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] $$

(A-5)

$$ \rho (FV^{-1})=\frac{\beta S + (1-\sigma)\beta V} {\mu+\kappa+\nu+\xi} $$

(A-6)

Since $\rho (FV^{-1})={\mathcal R}_{VT}$ and that at disease-free equilibrium,

$$ S_0 = \frac{\Uplambda(\omega+\mu)}{\mu(\phi+\omega+\mu)} $$

and

$$ V_0 = \frac{\phi\Uplambda}{\mu(\phi+\omega+\mu)} $$

Thus, the vaccination and treatment-induced reproduction number ${\mathcal R}_{VT}$ is given by:

$$ {\mathcal R}_{VT}=\frac{\beta\Uplambda(\omega+\mu+(1-\sigma)\phi)} {\mu(\phi+\omega+\mu)(\mu+\kappa+\nu+\xi)}. $$

(A-7)