-
PDF
- Split View
-
Views
-
Cite
Cite
Teruji Thomas, Some Possibilities in Population Axiology, Mind, Volume 127, Issue 507, July 2018, Pages 807–832, https://doi.org/10.1093/mind/fzx047
Close - Share Icon Share
Abstract
It is notoriously difficult to find an intuitively satisfactory rule for evaluating populations based on the welfare of the people in them. Standard examples, like total utilitarianism, either entail the Repugnant Conclusion or in some other way contradict common intuitions about the relative value of populations. Several philosophers have presented formal arguments that seem to show that this happens of necessity: our core intuitions stand in contradiction. This paper assesses the state of play, focusing on the most powerful of these ‘impossibility theorems’, as developed by Gustaf Arrhenius. I highlight two ways in which these theorems fall short of their goal: some appeal to a supposedly egalitarian condition which, however, does not properly reflect egalitarian intuitions; the others rely on a background assumption about the structure of welfare which cannot be taken for granted. Nonetheless, the theorems remain important: they give insight into the difficulty, if not perhaps the impossibility, of constructing a satisfactory population axiology. We should aim for reflective equilibrium between intuitions and more theoretical considerations. I conclude by highlighting one possible ingredient in this equilibrium, which, I argue, leaves open a still wider range of acceptable theories: the possibility of vague or otherwise indeterminate value relations.
It sometimes happens that one possible population is better than another with respect to the distribution of welfare.1 A population axiology, in a sense I will later make precise, is a theory of such comparisons. For example, suppose that two populations have the same size, and that in the first population everyone has a happy and fulfilling life, while in the second population every life is unhappy and devoid of meaning. Then any plausible population axiology will rule that the first population is better than the second. Note that, as in this example, I will often speak of ‘happy’ lives, and so on, just to mean those lives with a high level of welfare, without commitment to any particular theory of well-being.
It turns out to be hard to find a population axiology that accords with certain strong and widely held intuitions. For example, consider a large population of happy and fulfilling lives, and a second, perhaps larger one, in which life is barely worth living. Many people strongly intuit that the first population must be better than the second. On the other hand, it appears that if the second population is sufficiently large, it will inevitably have more total welfare than the first. And so one obvious criterion for betterness seems to entail what Parfit (1984) calls the Repugnant Conclusion: the second population may be better than the first.2
Can we avoid the Repugnant Conclusion? By itself, of course. But concrete attempts to do so have turned out to violate other intuitions of comparable strength. This has led several authors to produce formal arguments that seem to rule out any completely satisfactory population axiology.3 These arguments reach their culmination in Gustaf Arrhenius’s Population Ethics, intended to be the major survey of the current state of the field.4 His six increasingly subtle ‘impossibility theorems’ claim to show that our core intuitions stand in contradiction. The implications of this claim are potentially profound. At a basic level, we are simply learning what kinds of bullets we must bite. But if we cannot adjudicate between the core intuitions, we may be pushed into a wider methodological and metaethical inquisition.
In this paper I will review some of the basic ideas used in these impossibility theorems, and identify some problems with them. Because Arrhenius has approached the subject systematically and aimed for the best possible results, it is convenient to focus on his work: it means that the issues I raise are relevant to similar arguments found elsewhere in the literature, as I will make clear along the way.
The theorems deploy two basic strategies, and I will divide up my analysis accordingly. The first basic strategy relies on the background assumption—typically suppressed—that one can get from a low welfare level to any higher welfare level by a finite number of appropriately ‘small’ increments. I will call this premiss ‘Small Steps’. In §2, I argue that Arrhenius’s defence of Small Steps is inadequate, and show that, without it, there are counterexamples to four of his six theorems. One such counterexample is a lexic version of total utilitarianism.
Of course, this leaves open the question of whether it is ultimately plausible to deny Small Steps. But this question would be less urgent if the second basic strategy, used in the remaining two theorems, were a success. Instead of using Small Steps, this second strategy appeals to egalitarian intuitions. However, as I argue in §3, the key principle, the Inequality Aversion Condition, is poorly motivated, and, despite its name, is not necessary for an acceptable degree of inequality aversion. Indeed, while my example of total lexic utilitarianism does not satisfy the Inequality Aversion Condition, it nonetheless satisfies two more compelling egalitarian conditions from which the Inequality Aversion Condition is typically derived. Because of this, none of the six theorems tells strongly against total lexic utilitarianism, provided only that we deny Small Steps. Now, total lexic utilitarianism is one of a family of views that Arrhenius has called ‘Welfarist Superitarianism’ (Arrhenius, 2013, ch. 6). So another way to state the point is that Arrhenius’s arguments against Welfarist Superitarianism are ineffective, and a number of his claims about it are mistaken.
In such a context, the denial of Small Steps is a tempting possibility. Indeed, most other assumptions of the impossibility theorems are much more intuitively compelling. On one side we have the headlining adequacy conditions, like the need to avoid the Repugnant Conclusion. These assumptions are meant to be justified by strong evaluative intuitions that many people, at least, would find it repugnant to set aside.5 Small Steps is not like that: its denial might be surprising, but not in itself repugnant. On the other side, we have a handful of formal assumptions, the most widely discussed of which is the transitivity of the relation better than. Although indeed some, like Rachels (2004) and Temkin (2012), have taken the impossibility theorems as evidence of intransitivity, many others of us share Broome’s sense that transitivity is simply ‘an analytic feature’ of comparatives (Broome, 2004, §4.1). Giving it up means giving up—or at least fundamentally revising—the traditional conception of value. Again, Small Steps is not like that: it is not central to the concept of value or to the concept of well-being.
But one should not be too sanguine. For even if it is difficult to justify Small Steps within the abstract and minimalistic formal framework of the impossibility theorems, there are important arguments in its favour once we consider the dependence of well-being on continuous parameters such as the duration of some pleasure. One aim of this paper, then, is to highlight the role of such further considerations. Having sketched one type of argument for Small Steps in §4, I then suggest a final way in which its use is problematic. Even if Small Steps is true for every standard of smallness, arguments based on it are especially susceptible to worries about axiological vagueness. The upshot is that, granting Small Steps, there need not be determinate counterexamples to the most important adequacy conditions. Allowing for borderline counterexamples provides a conservative way to weaken those conditions— conservative because our intuitions may not easily distinguish between certain cases of determinate and borderline truth.6
1. The framework and key examples
To set the stage, I will first describe the framework in which all of the impossibility theorems take place. The idea is to assume as little as possible beyond what is needed to state the main adequacy conditions. I have omitted some possible complications that are irrelevant to the issues I want to discuss, but otherwise this framework is meant to be common ground. I will start a bit informally, and then say officially what data constitute a population axiology.
The first idea is that one life may be better than another. When, as here, I evaluate individual lives, as opposed to populations, the question is always how good the lives are for the people living them. If two lives are equally good in this sense, I say they have the same welfare level. So a welfare level can be understood as an equivalence class of lives, all equally good. I assume that the relation ‘at least as good as’, applied to lives or, derivatively, to welfare levels, is a preorder, that is, reflexive and transitive. (I do not require it to be complete, although it will be in my examples.) A population is a collection of lives, and a population axiology will also give a preorder on populations—a specification of when one possible population is at least as good as another. All the example axiologies I will consider will be ‘anonymous’: they hold that the value of a population depends only on how many lives instantiate each welfare level (so that, in particular, the identities of the people do not matter). Since my arguments will be based on what the impossibility theorems say about these examples, I may as well, in contrast to Arrhenius, assume that all population axiologies of interest are anonymous in this sense.7 Doing so will significantly simplify the formulation of various principles. With this in mind, let me define a distribution to be a finite, unordered list of welfare levels, perhaps containing repetitions. Each finite population determines a distribution.8 The assumption of anonymity means that we can make evaluative comparisons between distributions, in such a way that one population is at least as good as another just in case its distribution is at least as good. Again purely as a matter of simplification, I will assume that every logically possible distribution—every finite unordered list of welfare levels—lies in the domain of this preorder.
Here is some useful terminology. If a is a welfare level, then a population or distribution ‘at level a’ is one in which only level a occurs (perhaps many times). And if A and B are distributions, then 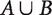 is the distribution obtained by concatenating the lists A and B. Finally, the size of a distribution is the number of people involved, that is, the length of the list.
is the distribution obtained by concatenating the lists A and B. Finally, the size of a distribution is the number of people involved, that is, the length of the list.
The impossibility theorems articulate various adequacy conditions for a population axiology, and state that these adequacy conditions are mutually incompatible. It is important to realize that these adequacy conditions are officially about the form of the population axiology; they don’t explicitly concern themselves with the interpretative question of which welfare levels correspond to which lives. However, to formulate the adequacy conditions in an understandable way, it helps if we can refer to a few broad features of this correspondence. For example, one of the main adequacy conditions is that the population axiology must avoid the Repugnant Conclusion. The Repugnant Conclusion in turn refers to a class of happy, fulfilling (henceforth ‘blissful’) lives and a class of lives barely worth living (henceforth ‘drab’). Officially:
It is possible to eliminate this classification by quantifying over sufficiently high and sufficiently low welfare levels, as Arrhenius effectively does. But, for ease of presentation, I will take the classification as a part of the axiology.The Repugnant Conclusion: For any distribution at a blissful welfare level, there is a better one at a drab level.
Officially, then, a population axiology consists of the following data: first, a set of welfare levels; second, a preorder on that set; third, a preorder on the corresponding set of distributions; fourth, a particular welfare level, singled out as ‘neutral’. We can then say that a welfare level is ‘positive’ or ‘worth living’ if it is higher than the neutral one.9 And fifth, among the positive welfare levels there is a class of ‘blissful’ ones, and a disjoint class of ‘drab’ ones. For my purposes, the only further assumptions are that there exists a blissful level, and that for any blissful level there is a lower drab level and another, even lower drab level. Some of Arrhenius’s more complicated arguments require three blissful and three drab levels, but those complications are irrelevant to what I shall say.
To illustrate this framework, let me lay out two examples. First, according to total utilitarianism, welfare levels can be represented by numerical ‘utilities’, in such a way that higher numbers correspond to better welfare levels, and one distribution is at least as good as another just in case its total utility is at least as high. For convenience, I require that the utility of each welfare level is an integer, and that any integer can occur. I stipulate that utility 0 represents the neutral welfare level, that 1 and 2 represent drab levels, and that 100 represents a blissful one.10
Here is a second example, which I call total lexic utilitarianism (TLU). Let me begin with an informal picture. (As I emphasize below, this picture gives one possible interpretation of TLU, rather than being part of TLU per se. Its purpose is just to give a handle on the formalism coming up.) There are two things that make life good—call them ‘love’ and ‘money’. The neutral level of welfare corresponds to a life with no love and no money; a blissful life has at least a little love, while a drab life has none. Moreover, a little love is worth any amount of money.11 So one population, or one life, is at least as good as another if it contains either more love in total or the same amount of love and at least as much money.
Formally, TLU has a similar structure to total utilitarianism: it claims that welfare levels can be represented by utilities, in such a way that higher utility means higher welfare, and distributions are ranked by total utility. The difference is that this time I require the utilities to be, not integers, but arbitrary pairs of integers (corresponding, in the picture above, to quantities of love and money respectively). For this to make sense, I have to explain how these pairs are ordered and how they can be added together. The ordering is lexicographic: (a1, a2) is at least as great as (b1, b2) just in case either 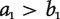 or else a1 = b1 and
or else a1 = b1 and 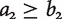 . Addition is component-wise:
. Addition is component-wise: 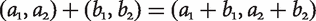 . It thus makes sense to compare distributions based on their total utility. To round out the example, I will stipulate that (0, 0) represents the neutral welfare level, that (1, 0) represents a blissful level, and that the drab welfare levels are those represented by pairs of the form
. It thus makes sense to compare distributions based on their total utility. To round out the example, I will stipulate that (0, 0) represents the neutral welfare level, that (1, 0) represents a blissful level, and that the drab welfare levels are those represented by pairs of the form 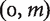 , with m > 0. To put it another way, a positive welfare level is drab just in case it is only finitely many levels above neutrality.
, with m > 0. To put it another way, a positive welfare level is drab just in case it is only finitely many levels above neutrality.
To be clear, this paper is not a defence of total lexic utilitarianism. Rather, I introduce it because it is a very simple theory that illustrates a wide variety of important ideas. The reader will naturally wonder whether welfare could really have the structure accorded it by TLU. I think that is a very good question. In fact, the basic argument of SS2 and 3 is that the impossibility theorems are ineffective without a negative answer to this question, or, more precisely, without a proper argument for the ‘Small Steps’ condition I mentioned in the introduction. Before we get to that more detailed discussion, let me explain in general terms why the impossibility theorems get so little traction on TLU.
The first point is that TLU does not entail the Repugnant Conclusion. According to my stipulations above, a drab life contains no love. Therefore a population of drab lives contains no love, and must be worse than any population of lives at the blissful level (1, 0). At this point one might object that (1, 0) could not reasonably correspond to a blissful life. After all, a life with a minimal amount of love is not much better than a life with none at all. We must recognize that a life at level (1, 0) is barely worth living, and then we will obtain a version of the Repugnant Conclusion.
But this objection is based on a misunderstanding. My interpretation in terms of ‘love’ and ‘money’ was picturesque and convenient. I will continue to use these terms in informal discussion. But this interpretation is not part of the axiology. TLU as such does not theorize about the components of well-being at all, and in particular does not claim that utility (1, 0) involves low levels of some component.12 A related misapprehension might arise if one imagines pairs of integers as labelling points on a plane in the usual way. Then (1, 0) is geometrically adjacent to (0, 0), and one might presume that the welfare levels represented by these pairs must therefore be similar in value. However, nothing in the definition of TLU validates this presumption. The fact is that there are infinitely many welfare levels between those two; they are not adjacent in any evaluative sense. So there is no reason (1, 0) cannot represent a high level of welfare.
The second point is that TLU shares many properties with ordinary total utilitarianism, inasmuch as it is a theory of ‘total utility’. The only way in which total utilitarianism runs foul of the impossibility theorems is that it leads to the Repugnant Conclusion. TLU avoids this problem, but it also remains similar enough to total utilitarianism that it satisfies almost all of the other adequacy conditions. There is one condition, the Inequality Aversion Condition, which ordinary total utilitarianism satisfies and TLU does not. But, as I argue in §3, this is a reason to reject the Inequality Aversion Condition, not a reason to reject TLU.
2. Against Small Steps
Now let me begin my analysis of the impossibility theorems. One strategy used by these theorems relies on the following principle.
Of course, ‘small’ is context-dependent. It invokes an implicit standard for smallness—that is, for each welfare level a, a specification of which other welfare levels count as differing from a by a ‘small’ amount. The standard must be weak enough to make Small Steps true. But it must also be strict enough to make various adequacy conditions seem compelling. For example, here is a simplified version of Arrhenius’s first impossibility theorem.14 The simplified claim is that no population axiology can avoid the Repugnant Conclusion while satisfyingSmall Steps: Any blissful welfare level a can be reduced to any lower drab level z in a finite sequence of small steps.13
Informally, we should accept a small decrease in welfare levels in exchange for a sufficient increase in population size. It is easy to see how one might argue from the Quantity Condition to the Repugnant Conclusion. Starting from a distribution at a blissful level a, we should accept a small decrease in welfare levels in exchange for a sufficient increase in population size. But, according to Small Steps, a sequence of such small decreases can lead us from a to a drab level z. We should therefore accept a decrease in welfare levels from a to z in exchange for a sufficient increase in population size. That is the Repugnant Conclusion. So no population axiology can satisfy the Quantity Condition and Small Steps while avoiding the Repugnant Conclusion.The Quantity Condition: Suppose that a and b are positive welfare levels, that b is lower than a, and that the difference between a and b is small. Then for any distribution at level a, there is a larger, better distribution at level b.
The first, fourth, fifth and sixth of Arrhenius’s theorems follow this sort of strategy, proceeding through a sequence of small steps. (Recognizing that the Quantity Condition is open to criticism, the latter three theorems rely instead on the so-called Non-Elitism Condition, which I will discuss in §3.) Each theorem is implicitly of the following form:
There are several types of objection one might make to such a theorem while conceding the force of the underlying intuitions. One possible objection is that an argument via Small Steps has the character of a sorites argument. Although I think this objection has merit, its force is not immediately clear; for a critical discussion, see Temkin (2012, ch. 9). I will make some related comments in §4. A second objection calls into question the way in which the adequacy conditions formalize the underlying intuitions. Let me say a little about this second objection, and then focus on the main line of thought: we can defuse the impossibility theorems by giving up Small Steps.Given any population axiology, there can be no standard of smallness according to which (a) Small Steps is true; and (b) certain intuitively compelling adequacy conditions are all true, perhaps including the Quantity Condition or the negation of the Repugnant Conclusion.
To see why the formal adequacy conditions might not properly reflect the underlying intuitions, consider the case of the Quantity Condition. As far as I can tell, the intuition is that any sufficiently small decrease in the quality of lives can be compensated by a sufficiently large increase in the quantity of lives. But that is not what the Quantity Condition actually says. The intuition as just stated is better represented by the weaker
The worry is that the Quantity Condition gains plausibility by conflation with the strictly weaker Trade-Off Condition. At any rate, it is not obvious to me that intuition supports the Quantity Condition over and above the Trade-Off Condition. The Trade-Off Condition is weaker, because what counts as a ‘small’ difference between a and b can depend on the size of the population at level a. The Quantity Condition, in contrast, requires there to be a single standard of smallness that works for all populations. Small Steps refers to that same universal standard. To see that this matters, consider Ng’s axiology, which he calls ‘TheoryTrade-Off Condition: Suppose we have a distribution at a positive welfare level a. There is some standard of smallness such that if the difference between a and a lower positive welfare level b is small, then there is a larger, better distribution at level b.
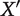 ’ (Ng 1989). He assumes that welfare levels are represented by real numbers, with 0 as the neutral level. We might take level 100 to be blissful, and those between 0 and 2 to be drab. Ng then gives a rule for aggregating these numbers, with populations ranked by their aggregate scores. The rule, in one concrete version, is that a population of n people with average welfare a has aggregate score
’ (Ng 1989). He assumes that welfare levels are represented by real numbers, with 0 as the neutral level. We might take level 100 to be blissful, and those between 0 and 2 to be drab. Ng then gives a rule for aggregating these numbers, with populations ranked by their aggregate scores. The rule, in one concrete version, is that a population of n people with average welfare a has aggregate score 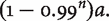 It is easy to see that this axiology satisfies the Trade-Off Condition and avoids—as Ng argues—the Repugnant Conclusion. It also satisfies Small Steps, for any standard of smallness (see footnote 31 below). However, Arrhenius’s first impossibility theorem rules out Theory
It is easy to see that this axiology satisfies the Trade-Off Condition and avoids—as Ng argues—the Repugnant Conclusion. It also satisfies Small Steps, for any standard of smallness (see footnote 31 below). However, Arrhenius’s first impossibility theorem rules out Theory 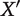 , because it does not satisfy the Quantity Condition for any standard of smallness. The failure of Theory
, because it does not satisfy the Quantity Condition for any standard of smallness. The failure of Theory 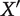 to satisfy the Quantity Condition over and above the Trade-Off Condition does not, in itself, seem like a compelling ground for criticism.15 At a minimum, the Trade-Off Condition might be a relatively attractive fallback position. One can tell a similar story about the other adequacy conditions that refer to small differences.
to satisfy the Quantity Condition over and above the Trade-Off Condition does not, in itself, seem like a compelling ground for criticism.15 At a minimum, the Trade-Off Condition might be a relatively attractive fallback position. One can tell a similar story about the other adequacy conditions that refer to small differences.Now let me turn to my main objection. While I accept that on its face Small Steps is plausible, I do not think it is compelling enough to be considered a basic adequacy condition. Barring some deeper justification—which Arrhenius does not provide—the simplest response to the impossibility theorems is just to give up Small Steps.
First, let me show that the use of Small Steps is no mere convenience: without it, the impossibility theorem fails. Consider the example of total lexic utilitarianism that I introduced in §1. I explained there that this axiology does not entail the Repugnant Conclusion. On the other hand, it does satisfy the Quantity Condition, for the following standard of smallness: the difference between a and b is small if and only if there are finitely many welfare levels between them.16 (To put it another way, a and b must have the same amount of ‘love’—as I suggested in §1, differences in love are in no way small. For example, by this standard, any drab life is only a small distance above the neutral level.) Thus the only objection that the first impossibility theorem raises against TLU is that it violates Small Steps. In fact, TLU satisfies all the adequacy conditions (excluding Small Steps) that are required by Arrhenius’s first, fourth, fifth and sixth impossibility theorems.
Why then accept Small Steps? One might, with Arrhenius, be inclined towards
According to Discreteness, one can get from a to b through a finite sequence of consecutive welfare levels. Let us grant the plausible further assumption that the difference between consecutive levels counts as small by any relevant standard. We then obtain Small Steps. The question, though, is why we should believe Discreteness. Arrhenius has very little to say about this. On the other hand, he does not actually rely on Discreteness. He claims that even if Discreteness is not true, we can focus attention on some subset of all welfare levels in which Discreteness holds, and in which the difference between consecutive levels is small. But this claim is little more than a restatement of Small Steps. It gives no new argument.18Discreteness: For any welfare levels a and b, there are at most finitely many welfare levels worse than a and better than b.17
Are there some other, more convincing arguments in favour of Small Steps? No doubt; I will explain one kind of argument in §4. First I want to consider the question of whether the impossibility theorems that do not use Small Steps are effective. If they are, then questions about Small Steps are less urgent (although, I think, independently interesting).
3. Against the Inequality Aversion Condition
Now let me consider the second basic strategy of the impossibility theorems. (The reader primarily interested in Small Steps can skip to §4.) It involves the following adequacy condition:19
Informally: the decrease of some people’s welfare levels from a to z can be compensated by the increase of sufficiently many others’ from b to z.The Inequality Aversion Condition: Suppose that a, z, b are welfare levels, with a higher than z and z higher than b. For any distribution A at level a, there are distributions Z at level z and B at level b such that Z has the same size as
and Z is better than
.
Before discussing the merits of this condition, let me explain how it is used in the impossibility theorems. The simplest argument appeals to the following principle:
The claim is that no population axiology can satisfy the Inequality Aversion Condition and the Mere Addition Principle while avoiding the Repugnant Conclusion. This is a simplified version of Arrhenius’s second impossibility theorem.20 Here is how the argument goes. Take a to be a blissful welfare level, z to be a drab level lower than a, and b to be a drab level even lower than z. (Recall that my official definition of ‘population axiology’ in §1 stipulated that such levels exist.) For any distribution A at level a, the Inequality Aversion Condition gives us distributions Z and B, with Z at least as good asThe Mere Addition Principle: Suppose that A and B are distributions containing only positive welfare levels. Then
is at least as good as A.
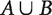 . The Mere Addition Principle tells us that
. The Mere Addition Principle tells us that 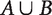 is better than A. So, by transitivity, Z is better than A. That is the Repugnant Conclusion.
is better than A. So, by transitivity, Z is better than A. That is the Repugnant Conclusion.Arrhenius’s second and third theorems elaborate on this basic strategy, replacing the Mere Addition Principle with intuitively weaker ones. These two theorems take the Inequality Aversion Condition as a basic adequacy condition. The special interest of these theorems in this paper is that they do not rely on Small Steps. Total lexic utilitarianism, my counterexample to Small Steps, is ruled out by the Inequality Aversion Condition instead.21
Should we accept the Inequality Aversion Condition as a fundamental constraint on population axiology? In particular, does it offer a compelling objection to total lexic utilitarianism? I will suggest that the Inequality Aversion Condition is not particularly compelling in its own right. Then I will criticize two important arguments for the condition. Finally, I will give a general argument that it cannot be justified on egalitarian grounds alone.22
First, is the Inequality Aversion Condition compelling in its own right? To answer that question, consider how the condition is used in the argument just described. It is used to show that large penalties for some people (the people in A, reduced from blissful to drab lives) can be compensated with small benefits to sufficiently many others (the people in B, raised from one drab level to another). I think it is far from clear that we should favour such trade-offs. For example, can all-but-imperceptible benefits to sufficiently many people make up for the loss of all real joy in the world? Admittedly, it may be that some of the intuitions here are not axiologically driven; talk of ‘penalties’ may, for example, evoke questions about rights.23 Nonetheless, if, as it seems to me, the verdict on the Inequality Aversion Condition in relevant cases is intuitively negative or unclear, we should not accept it as a fundamental adequacy condition. But perhaps we can derive it from more compelling premisses.
Arrhenius (cognizant of worries like the one I just raised) considers two such arguments. I will show that these two arguments fail to establish the Inequality Aversion Condition as an adequacy condition, at least if we are in doubt about Small Steps.
First, Arrhenius’s favoured argument for the Inequality Aversion Condition (2000a, §6.3) begins from
I agree that this condition sounds compelling. It should also be clear, at least in outline, how the argument from Non-Elitism to Inequality Aversion is supposed to go. The basic difference between the two conditions is that the Non-Elitism Condition only allows us to compensate for the loss of a small amount of one person’s welfare, while the Inequality Aversion Condition allows us to compensate for the loss of a large amount of many people’s welfare. But a sequence of small losses to one person at a time can amount to large losses for many people. Thus recursive application of Non-Elitism leads to the Inequality Aversion Condition.25The Non-Elitism Condition: Suppose that a, z, b are welfare levels, with a better than z and z better than b, and that the difference between a and z is small. Then, for some number n, it is always a net improvement to reduce one person’s welfare from a to z while increasing that of n others from b to z.24
However, this argument relies on Small Steps: it assumes that a sequence of small decreases in welfare can amount to a large one. Indeed, total lexic utilitarianism does not satisfy the Inequality Aversion Condition, but it does satisfy the Non-Elitism Condition.26 To see this, recall that the difference between a and z is ‘small’ only if they have the same amount of love. Suppose, then, that a and z differ only by m units of money. Since the difference between z and b is at least one unit of money, a decrease in the welfare of one person from a to z can be compensated by an increase in the welfare of m + 1 people from b to z. Thus while the Non-Elitism Condition may ultimately support the Inequality Aversion Condition, it certainly does not help us avoid the use of Small Steps.
Now let me turn to Arrhenius’s second argument for the Inequality Aversion Condition (Arrhenius 2000a, §6.1, following Ng 1989). It starts from
Note that the Non-Anti-Egalitarianism Principle presupposes a notion of ‘total welfare’, and my definition of a population axiology does not involve such a notion.27 So, as Arrhenius notes, one way to resist arguments from Non-Anti-Egalitarianism is simply to deny that welfare has the right kind of structure for total welfare to make sense. I agree that one could do that, but it seems worth pointing out that the argument still has problems, even if one countenances talk of total welfare. After all, many people have agreed with Ng that the Non-Anti-Egalitarianism Principle is extremely compelling, and have followed him in using it to derive the Repugnant Conclusion via the Inequality Aversion Condition.28The Non-Anti-Egalitarianism Principle: A perfectly equal distribution is better than an unequal distribution of the same size and with lower total (and thus lower average) welfare.
The main problem is that it is not true that the Non-Anti-Egalitarianism Principle entails the Inequality Aversion Condition. We can see this by once again appealing to total lexic utilitarianism. This theory ranks populations by total utility, and we can apply the Non-Anti-Egalitarianism Principle on the supposition that total utility is the mathematical representation of total welfare. Then TLU satisfies the Non-Anti-Egalitarianism Principle. (After all, it considers the population with higher total welfare to be better, whether or not it is perfectly equal.) But, as we have already seen, TLU does not satisfy the Inequality Aversion Condition.
Of course, proponents of the Non-Anti-Egalitarianism Principle invariably assume that welfare is to be represented by real numbers, and total welfare by their sum, instead of using pairs of numbers, as in TLU. On this assumption, Non-Anti-Egalitarianism does indeed entail the Inequality Aversion Condition.29
But the appeal to such a real-valued representation of welfare requires justification. There are two different ways of spelling out what the problem is, depending on how one thinks about total welfare. On the one hand, we might be able to find some common ground, such as the axioms of expected utility theory, that allows us to assign real numbers to welfare levels. We could then define ‘total welfare’ in terms of these numbers. But then it would be an open question why total welfare, defined in this particular way, is at all relevant to evaluating populations, let alone in the specific way claimed by Non-Anti-Egalitarianism. Greaves (2015) discusses this type of issue carefully in the context of prioritarianism. On the other hand, perhaps the thought is that we have some pre-existing notion of total welfare according to which the Non-Anti-Egalitarianism Principle is true; then it is an open question why total welfare in this sense can be represented by a sum of real numbers.30 I am not saying that either of these questions is unanswerable. My point is rather that it seems implausible that this line of thought could put the Inequality Aversion Condition beyond controversy, and in any case, an argument that simply presumes the resolution of these difficult issues cannot be satisfactory.
Here is a final, less technical worry about the Non-Anti-Egalitarianism Principle, and so derivatively about the Inequality Aversion Condition. The principle concerns cases in which considerations of total welfare, average welfare, and equality point in the same direction. The thrust of the principle is that in these cases no additional considerations can make a difference. But that is not obvious. For example, perhaps it is also relevant how many lives are above a certain level of sufficiency. In particular, in our application of the Inequality Aversion Condition, populations like 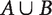 contain many high-quality lives, while populations like Z contain none. When thinking about the Repugnant Conclusion, a natural idea is that this very fact has overriding axiological significance. (I will describe a toy model with this feature in §4.) More generally, considerations of utility and equality may, in some cases, be overridden by others. This possibility undermines the Non-Anti-Egalitarianism Principle.
contain many high-quality lives, while populations like Z contain none. When thinking about the Repugnant Conclusion, a natural idea is that this very fact has overriding axiological significance. (I will describe a toy model with this feature in §4.) More generally, considerations of utility and equality may, in some cases, be overridden by others. This possibility undermines the Non-Anti-Egalitarianism Principle.
I can now broaden these remarks to explain why it is not possible to justify the Inequality Aversion Condition on egalitarian grounds alone. Standard ways of thinking about inequality aversion, like the so-called Pigou-Dalton criterion, agree that total utilitarianism is neutral about inequalities in welfare, at least on the assumption that total utility is the relevant measure of total welfare. This is just because total utilitarianism considers populations with the same size and total welfare to be equally good regardless of how equally that total is distributed. Exactly the same point applies to total lexic utilitarianism: on the understanding that it ranks populations by total welfare, it is neutral about inequality. So we cannot rule out TLU as insufficiently egalitarian unless we are willing, controversially, to rule out total utilitarianism on these grounds as well. Therefore the Inequality Aversion Condition is not a necessary condition for an acceptable degree of inequality aversion.
This point can be strengthened if we note that total utilitarianism, defined in the very abstract way of this paper, has egalitarian as well as inequality-neutral interpretations. The inequality-neutral interpretation is based on the understanding that increasing someone’s utility by one unit always increases total welfare by the same amount. Instead, we might interpret the utility scale in such a way that the increase in welfare represented by a fixed increase in utility diminishes as we move up the scale. On such an interpretation, it is better to give a fixed quantum of welfare to someone who is badly off than to someone who is better off. According to the Pigou-Dalton criterion, the theory so interpreted is egalitarian. For exactly the same reason, there can be decidedly egalitarian interpretations of TLU.
In conclusion, the Inequality Aversion Condition cannot be justified on purely egalitarian grounds. It is not strongly supported by direct intuition. Nor is it, in general, a consequence of the Non-Elitism Condition or of the Non-Anti-Egalitarianism Principle, and the latter principle has problems of its own.
4. Small Steps and indeterminacy
Recall the story so far. I have argued that the Inequality Aversion Condition should not be one of the fundamental adequacy conditions of population axiology. On the other hand, this condition follows from the much more compelling Non-Elitism Condition if we accept Small Steps. We have also seen another impossibility theorem, based on the Quantity Condition, which employs Small Steps. I have argued that the assumption of Small Steps is no harmless technicality, nor is it clearly justified. Still, it would be uncomfortable to pin the hopes of population ethics on the falsity of Small Steps. Small Steps follows if the welfare levels are ordered like the real numbers or the integers.31 Many of the quantities we detect in the world around us have that sort of structure, and it is (if nothing else) often assumed that welfare is the same.
One can say more in favour of Small Steps. That is not the project of this paper, but here is the kind of argument that I find most compelling. I will give one specific version of the argument, and then indicate how it can be generalized. Suppose for now that welfare depends only on the balance of pleasure and pain in a life. Stipulate that a life would be ‘blissful’ if it consisted of one hundred years of intense pleasure followed by a single neutral minute, completely devoid of pleasure and of pain. Stipulate that a life would be ‘drab’ if it began with one minute of that same intense pleasure, followed by one hundred neutral years. (These stipulations are appropriate as long as the Repugnant Conclusion seems repugnant when understood in terms of these kinds of lives.) Then we find a natural continuum between drab lives and blissful ones, as we lengthen the initial period of pleasure from one minute to one hundred years. Now consider two lives on this continuum that differ by only one millisecond’s worth of pleasure. (Or one nanosecond’s worth; use as tiny an interval as you like.) The difference in welfare between two such lives is surely ‘small’ in the relevant sense. But then Small Steps holds, because there are finitely many milliseconds between one minute and one hundred years.
Let me sketch how to generalize this argument away from considerations of pleasure and pain. The key claim is that, whatever the nature of well-being, we can find a continuum of possible lives beginning with some drab life and ending with a blissful one. By a ‘continuum’ I mean technically that these lives can be parameterized by a bounded interval of real numbers. In the specific version of the argument above, the continuum involved variations in the duration of some pleasure. But we could instead vary any of the attributes on which welfare depends, such as, at bottom, the configurations of particles or fields across spacetime. At any rate, this continuum is required to satisfy two further conditions. First, the lives must get better and better as we go along the continuum. Second, they must do so continuously, in the sense that, for any life along the continuum, any other life that is sufficiently close to it along the continuum will differ from it in welfare by only a small amount.32 The structure of the real numbers ensures that we can get from one end of the continuum to the other in a finite sequence of such sufficiently small steps (this is the Heine-Borel Theorem mentioned in fn. 31).
Given the plausibility of such arguments for Small Steps, the impossibility theorems do pose genuine difficulties for population axiology. We should presumably aim for some kind of reflective equilibrium between basic intuitions and more theoretical considerations. In concluding this paper, I want to highlight one possible ingredient in this equilibrium that has not been widely addressed in the literature: the possibility of vague or otherwise indeterminate axiologies. Such indeterminacy has been considered before, but only in a limited way. For example, Broome (2004) advocates a version of total utilitarianism with a vague critical level. As he recognizes, this move only partly mitigates the impact of the impossibility theorems. I suggest that vagueness has a more general role to play in balancing competing intuitions.
Why is vagueness relevant at all? Let me begin with an analogous case. Suppose I believe that Fred—whom I have never met—is tall; I know precious little else about him. I walk into a room, certain that Fred will be there. But there are two men present. Which one is Fred? The first man I see is determinately not tall. If the second man were determinately tall, I would infer that he was Fred. But the second man is only borderline tall. Still, all else being equal, I will be inclined to think that the second man is Fred. This matches my prior beliefs and my new evidence better than the alternative. Moreover, some borderline tall people are taller than others. Some are borderline tall but almost determinately tall. The closer the second man is to being determinately tall, the more inclined I will be to believe that he is Fred. So too in the case of population axiology. If I think the Quantity Condition (for example) is compelling, then, all else being equal, I should be inclined to favour a theory according to which that condition is borderline, but almost determinately, true over a theory according to which it is determinately false.
This picture is strengthened if we observe that the impossibility theorems that use Small Steps are structurally similar to sorites arguments.33 The impossibility theorem I discussed in §2 repeatedly invokes the Quantity Condition to derive the Repugnant Conclusion. Similarly, a sorites argument might claim to prove that every tree is tall by repeatedly invoking
Theories of vagueness that respect classical logic must accept that there are counterexamples to the Tolerance Condition. But they must also explain the strong intuition in its favour. A typical explanation is that the Tolerance Condition has no determinate counterexamples. Every instance of the Tolerance Condition is at least borderline true, and indeed close to determinately true.34 If this kind of story explains why the Tolerance Condition is compelling, then it may help with the Quantity Condition and the Non-Elitism Condition as well. Even if these conditions admit counterexamples, they need not admit determinate counterexamples. That may go some way towards explaining their attraction.The Tolerance Condition: Suppose that a and b are heights, that b is lower than a, and that the difference between a and b is small (less than one millimetre, say). Then it cannot be the case that a is tall for a tree and b is not.
Let me now illustrate these general considerations with a toy model.35
In this axiology, welfare levels are represented by integers. Let us suppose that 0 represents the neutral level, 1 and 2 represent drab lives, and 100 represents a blissful life. Small Steps is bound to hold, assuming that the difference between consecutive welfare levels counts as ‘small’. The ranking of populations will have a sufficientarian flavour. There is some positive welfare level S, the level of sufficiency, above which life is ‘very good’; lives below – S are ‘very bad’. Populations are ranked, in the first instance, by the number of very good lives minus the number of very bad lives. Then ties are broken by total utility, the sum of integers.
Does such an axiology entail the Repugnant Conclusion? No—not as long as the blissful lives are above S and the drab lives are below it. By the first impossibility theorem (§2), we know that the Quantity Condition must fail. Indeed, it fails when, and only when, the small decrease in welfare from a to b brings us from a life that is very good to one that is not. But this is where vagueness can soften the blow. If the level of sufficiency is vague, then there are no consecutive welfare levels a and b such that, determinately, a is very good and b is not. Thus the Quantity Condition has no determinate counterexamples. Each instance is at worst borderline true, failing on at most one of the many possible precisifications of S.
For the same reason, the Non-Elitism Condition has no determinate counterexamples. Indeed, of the adequacy conditions appearing in Arrhenius’s theorems, only one is entirely invalidated by this axiology. That is the Inequality Aversion Condition, which, I have already argued, we should not accept on its own merits.
5. Conclusion
The main point of this paper is just how much the impossibility theorems rely on the background assumption of Small Steps. I gave a toy example—total lexic utilitarianism—which invalidates Small Steps but satisfies all but one of the main adequacy conditions. The same example helps us see why the remaining adequacy condition, the Inequality Aversion Condition, is not particularly compelling.
One possibility, then, is to deny Small Steps. It is a possibility worth considering too: on its face, it is less painful than denying transitivity or giving up, say, the Non-Elitism Condition. Certainly Arrhenius’s justification for the assumption is inadequate, and finding a better justification is important to his project. Moreover, Small Steps and the Inequality Aversion Condition, if they can be justified at all, rest on relatively subtle considerations about the structure of the welfare scale. This necessarily takes us beyond the austere formal framework of the theorems onto more controversial ground, and perhaps we can find a way forward.
However, I am not really optimistic about this possibility. As I explained in §4, consideration of how well-being depends on underlying continuous parameters suggests that the welfare scale is enough like a continuum to justify Small Steps. But the reliance of the impossibility theorems on Small Steps opens up a final possibility: the conflict of intuitions might be mitigated by axiological indeterminacy. I have introduced here the main idea, which I will explore more adequately in future work.36
Footnotes
There are other common ways of expressing this idea. In particular, some prefer to say that a population with one distribution of welfare would be better than a population with another distribution, all else being equal. I prefer my formulation, but nothing is supposed to hang on it here.
I say only ‘seems to entail’ because I will later consider a theory of total welfare that does not entail the Repugnant Conclusion. The well-known ‘critical-level’ theories (for which see Blackorby, Bossert and Donaldson 1995) are arguably also of this kind. Of course, one may wonder what it means to ‘total’ welfare at all; I will raise a related issue in §3.
Examples include Ng (1989), Carlson (1998), Kitcher (2000), Tännsjö (2002), and especially Parfit (1984), from which most of the arguments of this type ultimately derive. It is at least arguable that the same problems arise if if we skip axiology and deal directly with the question of which populations one ought to bring about (Arrhenius 2005). But in this paper I will focus on axiology.
Arrhenius’s book (forthcoming), is well known in draft form. In fact, the theorems themselves and much of the relevant discussion have been published in previous work (subject to some irrelevant revisions). I will refer to the theorems as they are enumerated in the manuscript, but cite the published discussions. The first four theorems are essentially those developed in Arrhenius (2000a); the fifth is from Arrhenius (2003); the sixth is from Arrhenius (2009, 2011). I note that the proof of his favoured sixth theorem contains an error in the derivation of the Restricted Quality Addition Condition (Arrhenius 2011, Lemma 1.3). As far as I know, one has to slightly strengthen the premisses of the theorem, in a way unlikely to cause further controversy. This will not affect my discussion.
In this paper, I just take it for granted that the main adequacy conditions meet this criterion (with the exception of the egalitarian conditions I discuss in §3). There is lively disagreement about whether the Repugnant Conclusion itself is truly repugnant; see especially Huemer (2008), who invokes (for one thing) the kind of argument for the Repugnant Conclusion that I discuss. It is worth noting that the more nuanced fifth and sixth theorems involve intuitive strengthenings of the Repugnant Conclusion, which strike many, including me, as more problematic. For example, the fifth invokes the ‘Very Repugnant Conclusion’: any large population of blissful lives is worse than one consisting of (say) ten times as many people in terrible agony as well as a lot of others whose lives are barely worth living. But such strengthenings would not change the main points I will make, and in general I will avoid irrelevant complications.
I will develop this idea much more fully in forthcoming work based on Thomas (2016, ch. 2).
The distinction between anonymous and non-anonymous axiologies is also (at least arguably) irrelevant if we stick to comparisons between populations that have no people in common. As the referees pointed out to me, this provides one way to extend the discussion of anonymous axiologies to non-anonymous ones.
Of course, one might also be interested in infinite populations, but these raise sui generis problems; see, for example, Bostrom (2011).
How exactly to understand the neutral level is one of the key substantive questions; I will say nothing about it here.
My use of integers here and below, instead of arbitrary real numbers, is unnecessary but convenient: it will help with my discussion of Small Steps, and it means that once I have specified that 0 represents the neutral level, the utility of every other welfare level is completely determined—for example, there must be a welfare level immediately above the neutral one, and it must get utility 1.
In this sense, love is ‘superior’ to money. The superiority of some welfare components over others is best known from Mill (1863, II.5), when he considers two pleasures such that one ‘would not resign [the first pleasure] for any quantity of the other’. See Arrhenius and Rabinowicz (2015) for a critical overview of different types of superiority, including—more relevantly to TLU as such—the superiority of blissful lives over drab ones.
To make this point more vivid, observe that we could use single real numbers instead of pairs of integers to represent the order of welfare levels. (For example, instead of the pair (a1, a2), we could use the real number 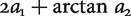 . One can show that these real numbers are ordered in the same way as the corresponding pairs.) With such a representation in mind, there is no temptation to think of welfare as having two components.
. One can show that these real numbers are ordered in the same way as the corresponding pairs.) With such a representation in mind, there is no temptation to think of welfare as having two components.
More formally: there is a finite decreasing sequence 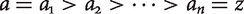 of welfare levels such that the difference between consecutive terms is small. Recently, Arrhenius (2016) has adopted the name ‘Finite Fine-grainedness’ for essentially this condition. Erik Carlson (forthcoming) independently raises some very similar objections to Small Steps.
of welfare levels such that the difference between consecutive terms is small. Recently, Arrhenius (2016) has adopted the name ‘Finite Fine-grainedness’ for essentially this condition. Erik Carlson (forthcoming) independently raises some very similar objections to Small Steps.
See Arrhenius (2000a, §10.3). His argument (including his version of the Quantity Condition) is more nuanced than the version I give here, as he is keen to make his premisses as weak as possible. I have eschewed certain subtleties in the interests of clarity, while preserving the features of the argument that I wish to discuss. A similar comment applies to my discussion of his other theorems.
This line of thought was first suggested to me by John Broome; essentially the same point is made by Binmore and Voorhoeve (2003). To be clear, Arrhenius’s main reason for rejecting Theory 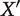 is that it violates a condition called ‘Weak Non-Sadism’. As I mentioned, his later, preferred theorems do not rely on the Quantity Condition.
is that it violates a condition called ‘Weak Non-Sadism’. As I mentioned, his later, preferred theorems do not rely on the Quantity Condition.
Thus Arrhenius (2013, §6.4) is wrong to claim that Welfarist Superitarian theories like TLU must violate the Quantity Condition. To see that the Quantity Condition applies, suppose that 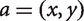 and
and 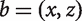 are positive welfare levels whose difference is small. A population A of m people at level a has aggregate welfare (mx, my). If x > 0, then a population B of m + 1 people at level b has aggregate welfare
are positive welfare levels whose difference is small. A population A of m people at level a has aggregate welfare (mx, my). If x > 0, then a population B of m + 1 people at level b has aggregate welfare 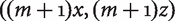 ; this is better than A. Or if x = 0, then y and z must both be positive. If we choose a number n such that nz > my, then a population B of n people at level b is better than A, as the Quantity Condition requires.
; this is better than A. Or if x = 0, then y and z must both be positive. If we choose a number n such that nz > my, then a population B of n people at level b is better than A, as the Quantity Condition requires.
My discussion here refers to Arrhenius (2011, §1.2), as well as to parallel sections in his other cited works. I have slightly simplified his formulation of Discreteness. A more standard term than ‘discrete’ would be ‘locally finite’.
As alternatives to Discreteness, a few other technical conditions have been erroneously proposed to me as entailing Small Steps. In this footnote I discuss them briefly in order to forestall further misunderstanding.
To begin with, in some of his discussion Arrhenius appears to think that welfare, if not satisfying Discreteness, must be ‘dense’: for any welfare levels a and b, if b is better than a, then there is a welfare level that is better than a and worse than b. Two anonymous referees likewise suggested to me that Small Steps follows automatically if the welfare levels, in addition to being dense, have no isolated points. Now even if this were true, the issue would only be pushed back: why accept the conjunction of denseness and no isolated points? TLU satisfies neither conjunct. More importantly, the proposed conjunction does not entail Small Steps: a counterexample is the lexicographic order on pairs (a1, a2), where a1 is an integer and a2 a real number, and, as in TLU, two pairs differ by a ‘small’ amount if they have the same first component.
Another possible condition is continuity. Assuming for simplicity that there is no incomparability, the standard meaning of continuity is that, if a and b are welfare levels and a is better than b, then any sufficiently small perturbation of a is better than b, and any sufficiently small perturbation of b is worse than a (see, for example, Mehta 1998, Definition 2.18 for a rigorous definition). It has been suggested to me that continuity in this sense entails Small Steps. But this is not right either. For example, the preorder on welfare levels in TLU does not satisfy Small Steps, but it is continuous with respect to the natural (discrete) topology on pairs of integers.
Heuristically, Small Steps is more closely related to the mathematical condition of compactness rather than denseness or continuity. The argument I give in §4 uses the fact that a closed interval of real numbers is compact (the Heine-Borel Theorem).
See Arrhenius (2000a, §10.5). Again, I have made some harmless simplifications in order to focus on the key issues.
The theorem replaces the Mere Addition Principle with the Dominance Addition Condition. While ‘mere addition’ simply adds the population B of positive lives, ‘dominance addition’ (or ‘benign addition’, in the terminology of Huemer 2008) simultaneously improves the lives in A. Curiously, Kitcher’s impossibility theorem (Kitcher 2000, p. 567) includes an adequacy condition (‘DVA’) that directly denies the Mere Addition Principle as applied here: he insists that if the Repugnant Conclusion is false, then adding drab lives to a large, blissful population decreases its value. This significantly reduces the interest of his theorem, since the Mere Addition Principle is widely seen as (at least) the default hypothesis, or even ‘obviously true’ (Tännsjö 2002, p. 357). Kitcher (2000, §9) also relies on Small Steps, recognizing, however, that this may be problematic.
Indeed, if again a is the blissful level and z and b are drab levels, then the population  is always better than the population Z, according to total lexic utilitarianism.
is always better than the population Z, according to total lexic utilitarianism.
A referee pointed out that one might appeal to prioritarian rather than egalitarian ideas to justify the Inequality Aversion Condition. At the level of this discussion, there is not much difference between prioritarianism and egalitarianism, so what I say will apply either way. To justify the Inequality Aversion Condition we need further assumptions, like Small Steps, which are neither egalitarian nor prioritarian in their motivation.
For Arrhenius’s discussion of this and related issues, see Arrhenius (2013, §6.6).
Arrhenius has two versions of the Non-Elitism Condition (one of them ‘General’), but the difference between either of them and the version I have given here is nugatory. Parfit’s arguments (1984, §142 ff.) also use a version of the Non-Elitism Condition: small losses to some are compensated with at least as large gains to others. (Parfit justifies such compensation using heuristics about utility and equality akin to the Non-Anti-Egalitarianism Principle, discussed below; these heuristics inspired Ng’s work.) He does not derive the Inequality Aversion Condition per se, but my objection applies to his argument as well, since it relies on a series of small steps. The second and third arguments for the Repugnant Conclusion in Tännsjö (2002) are variations on Parfit. (Tännsjö’s first argument uses the Quantity Condition as in §2, following Arrhenius.)
Elaborations of this argument appear as lemmas in the proofs of the fourth, fifth and sixth theorems. See Arrhenius (2000a, Lemma 5.1.1; 2003, Lemma 1; 2011, Lemma 1.1.1).
Thus Arrhenius wrongly takes it for granted that Welfarist Superitarian theories like TLU must violate the Non-Elitism Condition, since they violate the Inequality Aversion Condition. For example, he writes, ‘Given that the Non-Elitism Condition is such a plausible condition, I think there are only two options here: accept the Inequality Aversion Condition or reject transitivity. The latter move is, of course, quite counterintuitive and … amounts to giving up the project of finding an acceptable population axiology’ (Arrhenius 2013, §6.7). He does not properly recognize the option of denying Small Steps—on the face of it, a much less extreme option than rejecting transitivity.
The motivation for the Non-Anti-Egalitarianism Principle does not require talk of ‘total’ or ‘average’ welfare. (I thank Ralf Bader for emphasizing this point to me.) The idea is that the betterness relation might combine two values—let us call them ‘general welfare’ and ‘equality’. The principle is that a population that is better with respect to general welfare and better with respect to equality is better overall. This formulation makes sense whether or not general welfare is conceptualized as the sum of individual welfare levels. However, this more abstract version of the Non-Anti-Egalitarian Principle only slightly ameliorates the issues raised below.
See, for example, Huemer (2008) and the ‘first trilemma’ of Carlson (1998). Carlson’s second trilemma uses a similar argument to derive the ‘Reverse Repugnant Conclusion’: for any population of truly awful lives, there is a worse one consisting of lives only just below the neutral level. The derivation is a simple adaptation of Ng’s to deal with negative welfare levels, and so faces the same worries. In fact, Carlson must appeal to an adequacy condition even stronger than Non-Anti-Egalitarianism: one population is better than another if it has higher total and higher average welfare.
The argument proceeds as follows. Suppose that population A has m people with welfare a, and B has n people with welfare b. Then the total welfare of  is ma + nb, while that of Z is mz + nz. Thus the latter has higher total utility (and the Non-Anti-Egalitarianism Principle says it is better than the former) so long as
is ma + nb, while that of Z is mz + nz. Thus the latter has higher total utility (and the Non-Anti-Egalitarianism Principle says it is better than the former) so long as 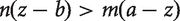 . If a, z and b are real numbers (or more generally, if the Archimedean axiom holds) then this inequality will hold for all sufficiently large n.
. If a, z and b are real numbers (or more generally, if the Archimedean axiom holds) then this inequality will hold for all sufficiently large n.
More specifically, the key question is why the relevant notion of total welfare (or ‘general welfare’, as I called it in fn. 27) is governed by the Archimedean axiom of measurement theory; see Krantz et al. (1971, §3.2, Definition 1). The axioms given by Krantz et al. are sufficient to derive a representation of general welfare as the sum of real numbers (their subsequent Theorem 1). However, without the Archimedean axiom, we still get an additive representation of general welfare, with values in what Krantz et al. (1971, §2.2.5) call an ‘ordered group’—the set of lexicographically ordered pairs of integers being but one example. See Carlson (2007), Pivato (2014) and Thomas (forthcoming) for discussions of this last point.
For the integers, I assume that the welfare difference corresponding to consecutive welfare levels counts as ‘small’. For the real-number case, I assume that, for any real number x, the real numbers that differ from x by a ‘small’ amount include all those in some open interval around x. In other words, any sufficiently small change from x counts as small. The Heine-Borel Theorem says that any closed, bounded interval of real numbers is contained in the union of finitely many of these small intervals. Thus any closed, bounded interval can be traversed in a finite number of small steps. Note that this argument depends on the assumption that all real numbers in an appropriate interval correspond to welfare levels; it will not work if there are gaps.
The usual mathematical notion of a continuous function would require that this criterion holds for any standard of smallness (assuming, technically, that the welfare levels that differ from a given one by a small amount form a topological neighbourhood). Here we only need it to hold for some standard of smallness with respect to which the relevant adequacy conditions (the Quantity Condition, the Non-Elitism Condition, or both) are true.
I will develop and defend this analogy in other work. For a critical view, see Temkin (2012, ch. 9). Here I rely only on a broad similarity to amplify the considerations of the preceding paragraph. In my informal survey, a few philosophers resist the very idea of moral vagueness. But many others agree that there is, at least, a strong prima facie case for it: see Constantinescu (2014), Dougherty (2014) and Schoenfield (2015) for some recent examples.
See, for example, Keefe (2000, pp. 185–6) in the case of supervaluationism. Note that for Keefe, as for many supervaluationists, plain old truth is what I have called determinate truth. For a theory that emphasizes closeness to determinate or ‘clear’ truth, see Edgington (1996). Of course, other treatments of the sorites are available, including treatments that forgo classical logic; I cannot give a survey here.
The model here resembles the views defended by Qizilbash (2005) and Knapp (2007), and also has some affinity to the ‘imprecisionist lexical view’ sketched by Parfit (2016).
I would like to thank Gustaf Arrhenius for sharing drafts of his work with me, and John Broome, Hilary Greaves, David McCarthy, Toby Ord, Theron Pummer, John Cusbert, Stefan Riedener, Frank Arntzenius, Christian List, and two anonymous referees for many useful comments. This work was partly funded by a research studentship from the Arts and Humanities Research Council, and by the Leverhulme Trust (RPG-2014-064).


