1 Introduction

An observation in the use of models in science is that particular model structures are used across multiple distinct scientific domains. To clarify, model here refers to what has been described as a model-type (Van Fraassen, 1980); a model in which parameter values may remain unspecified. In this context, model structure refers to the abstract structure of a model-type, meaning that, in the case of mathematical models, the variables and parameters of the structure do not refer to anything that can be observed empirically. The observation of a model structure that is imported into a new domain can be labelled as inter-domain model transfer. As an example, the growth process of firms is modelled using the same mathematical structure as the Yule process, which is a model originally developed in evolutionary biology (Simon, 1955). Such observations contrast a view of science in which various scientific domains operate in isolation, each using a domain specific methodology. Instead, the observation that particular model structures are used across multiple distinct scientific domains points to a view of science that is organized through a particular set of methods (Humphreys, 2004). That is, various distinct scientific disciplines make use of overlapping methods. This does not answer, however, why we would observe such an organisational structure. In fact, it is puzzling when we consider that models are, generally speaking, constructed for a domain-specific purpose: answering a question (Boumans, 2006). Such questions often concern phenomena. For example, how do firms grow in size over time (Simon & Bonini, 1958)? Questions about phenomena are inherently domain specific; they ask about a growth process of, in this example, a specific economic entity, firms. The ability of a model to answer this question is usually built into the structure of the model (Boumans, 1999), by shaping the model structure in such a way that it fulfils relevant validation criteria. Perhaps one would expect that a model structure shaped by validation criteria that are deemed relevant for a domain specific purpose would always produce a domain specific model structure, but for some particular model structures this is not the case.

The main question that this paper will seek to answer is what explains the inter-domain transfer of some model structures? Implicit in the observation that some model structures are transferred across multiple domains is that these model structures are somehow considered to be useful across the domains to which they are applied. Another way of putting this question is, therefore, what makes a model structure useful in the domain it was constructed for, as well as the domain it is transferred to? In order to answer this question, this paper will introduce a novel framework of model transfer. The foundation for this framework is the model construction account by (Boumans, 1999). It entails that models are constructed such that they meet various validation criteria. Validation is defined here as the broad assessment of model correctness in relation to its purpose. Validation criteria are points of reference to which model correctness for a particular purpose is assessed. For example, we could assess whether a model is in line with relevant theory or we could assess whether the model is able to reproduce certain facts about phenomena. It is the fulfilment of such validation criteria that determines whether a model is considered to be useful. Given this account, I will show that inter-domain model transfer can be explained by overlap between validation criteria across domains. Special attention will be paid to overlap between so-called phenomenological validation criteria. To explain how this overlap can occur, I will introduce the notion of universal patterns. Universal patterns are abstract structures that, when coupled with empirical content, can be made to apply to multiple distinct domains. Empirical content refers to the information that relates an abstract structure to objects that can be observed empirically (Humphreys, 2019). In order to illustrate my analysis I will discuss a case study of model transfer. The study concerns the Yule Process, a model that was first developed in evolutionary biology (Yule, 1925), and later transferred to various other systems including the growth of firms (Simon, 1955).

In the existing literature we can distinguish three main accounts that seek to explain model transfer (Knuuttila & Loettgers, 2020), analogues (Hesse, 1966) which attributes model transfer to similarity relationships between phenomena, formal templates (Humphreys, 2019), which attributes model transfer mainly to overlap in construction assumptions and model templates (Knuuttila & Loettgers, 2016), which attributes model transfer to overlap in conceptual features. What each of these accounts embed is a notion of inter-domain model usefulness. They point to particular aspects of model structures that allow scientists to re-use these structures across distinct domains. I will argue, however, that although valuable, these accounts do not give a complete enough description of what it is that makes a model considered to be useful in practice.

Looking at models as analogies is an account discussed in a.o. Hesse (1966). Within this account, models derive utility from the similarity relations they have with the phenomenon of interest. Hesse (1966) distinguishes positive, negative and neutral analogies. In the context of models, positive analogies are the aspects of the phenomenon of interest and the model mechanisms that overlap. Negative analogies are the aspects that do not overlap. Neutral analogies are the aspects for which this overlap is yet to be determined, and are thus what makes the model potentially useful to learn about the phenomenon of interest. In order for the structure of a model be useful, it must thus be a positive analogy of the phenomenon of interest in that particular domain to some degree. In the case of model transfer, this implies that features of the model structure are a positive analogy in both the original and new domain. This is likely to be the case when there is a similarity relation between targeted phenomena of the different domains. If we consider a model of genera growth in biological evolution, the structure of which is also used as a model for firm growth, for example Simon & Bonini (1958), it is likely that there are certain features in the model that serve as analogies to genera growth in biological evolution as well as firm growth. Importantly, such features cannot be domain specific, and are thus to some extent abstract. As we will see in the case study of this paper, one of these features is proportional growth, which can serve as an analogy to how both genera and firms grow. What is transferred according to this account, is thus an analogy that applies to multiple domains. This still leaves open, however, why it is that certain abstract features can serve as positive analogies in multiple domains. Furthermore, as also noted in Humphreys (2019), such analogies can often be made to fit in a domain opportunistically. Just looking at model transfer in the context of analogies may thus not always yield a satisfactory account of model transfer.

A different view comes from Humphreys (2004) in which the idea of a computational template is put forward. A computational template is a computational structure that can be adjusted to be used as a model in distinct domains. The utility of using this computational template and the explanation as to why some model structures become templates are favourable analytical-tractability properties. The template should also be flexible; it should be open to adjustments, such that it can be made to fit various distinct domains. This view of model transfer, however, was originally put forward, to be applicable to computational models. More recently, we have seen an extension of this account in Humphreys (2019). This view regards that what is being transferred a so-called formal template. In this account, the usefulness of a model structure is essentially determined by the correctness of a model’s construction assumptions. Model transfer, in this account, is therefore enabled by the correctness of the construction assumptions in the original and new domain on a more abstract formal level. If a construction assumption is a linear relationship between two variables then this assumption should hold in both domains. That what is transferred in essence is thus not an analogy, but a “correct” formal structure with favourable formal properties. Knuuttila & Loettgers (2020) state, however, that just considering formal properties is not a complete explanation because it does not explain why some model structures are transferred between domains widely and others are not. Many model structures that are successfully used within a particular domain will have favourable formal properties such as analytical tractability. Only few, however, are transferred across domains.

Another important addition to the model transfer literature is Knuuttila & Loettgers (2016), in which the concept of a model template is introduced. This is a template with favourable formal properties coupled with general conceptual features. These conceptual features suggest how to theorise about the phenomenon described by the model. This implies that model transfer is enabled when the conceptual features embedded in the template are deemed useful tools for theorising in both the original and new domain. Examples of such conceptual features are given in Knuuttila & Loettgers (2020) include phase transitions and local interactions. The account of model templates points to a particular source of model usefulness that allows us to explain some instances of model transfer. The account, however, is, in my view, most applicable to the methods and conceptual notions present in complexity science and, therefore, limited in its scope of application. The essential difference between the account of model transfer put forward in this paper is that it is does not rely on a particular epistemological account of model usefulness. Instead, rather than explaining what makes a model structure useful, I will take a more empirical approach and look at what makes a model structure considered to be useful in observed scientific practice. This approach in my view, results in an account of model transfer that is a closer match to scientific practice and, therefore, covers a wider range of model-transfer cases. It also does not rely on a particular epistemological view of model usefulness. Furthermore, it highlights an enabling factor of model transfer that is not explicitly present in the accounts of model transfer discussed, namely universal patterns. The account presented here is also general in the sense that it subsumes the existing accounts of model transfer here to some extent.

To specify the aforementioned criteria of model usefulness, I build on the literature on model validation, which I have defined as the assessment of a model’s correctness relative to its purpose. The benchmarks in the validation process are validation criteria. To this regard, Boumans (1999) shows that the ability of the model to fulfil such criteria is built into the model, and is thus central in shaping the model structure. To assess whether the model is able to fulfil these validation criteria to a satisfactory degree, the model is subjected to various validation tests (Senge & Forrester, 1980). Which validation tests are deemed relevant, differs given the purpose of the model (Barlas, 1996). Looking at model transfer from the point of view of validation, model transfer is enabled by satisfactory validation in the original and the new domain, which, in turn, is enabled by overlapping validation criteria. In this paper, I will argue that empirical validation may play a key role in the transfer process, meaning the assessment of whether the model is able to reproduce relevant facts about phenomena. In such cases, the model structure that is transferred must be able to reproduce facts about phenomena in the original as well as the new domain. Empirical validation as a mechanism of model transfer is supported by the notion of universal patterns. Universal patterns help us understand why certain model structures are transferred so widely.

An account of model transfer that also starts from scientific practice can be found in Donhauser (2020). It contrasts two opposing viewpoints regarding the ability of scientists within a particular domain to import knowledge from other scientific domains. Incommensurability states that epistemology is domain specific to such a large degree, that knowledge transfer between domains is impossible. On the other end, there is the notion of voluntarism, which states that scientists can “choose” a particular epistemological stance as long as certain general conditions are met. Donhauser (2020) argues that incommensurability is not able to explain model transfer while voluntarism does. As we will see, the idea put forward in this paper fits neither of these epistemological viewpoints perfectly. Instead, I will argue that models are likely to be transferred when there is overlap in the criteria used to assess model usefulness. The criteria scientists use do not necessarily have to be the result of voluntary decisions under general conditions, but may also be a function of particular paradigms. As is argued in Humphreys (2004), a paradigmatic organisation of science is not necessarily domain specific. Rather, certain methodological strategies span multiple distinct domains.

The reader may associate the notion of model validity with the notion robustness, or, more specifically, with the notion of model robustness such as put forward in Lloyd (2015). Model robustness refers to a degree of insensitivity of a model’s ability to reproduce facts about phenomena, to changes in various assumptions and/or parameter values of the model. Inter-domain model transfer could be seen as robustness with respect to changes in the empirical content of a model structure. If we change the empirical content of a model structure (transfer a model structure to a new domain), the model is still able to reproduce relevant facts about phenomena. Generally speaking, however, robustness refers to a property of model structures that reproduce facts about phenomena with the same empirical content. Therefore, to avoid confusion, I will not engage explicitly with the notion of model robustness in relation to model transfer. Assessment of model robustness, as it is generally understood, however, may be subsumed in the more general empirical validation process when relevant. Often the assessment of model robustness may come in the form of sensitivity analysis; altering parameter values and/or model assumption and assessing how this affects model output.

2 Framework: Validation Criteria and Model Transfer

Central in what I argue in this paper is that satisfactory model construction requires fulfilment of certain validation criteria (Boumans, 1999). The model structure is, therefore, shaped by its validation criteria. This implies that the model can only be reused in a new domain when it can be validated within this new domain. Given the account of model construction that I will present here, this is the case if and only if there is overlap in the validation criteria in both the original and the new domain. Let us now take a closer look at the account in Boumans (1999) to understand, first, what validation criteria consist of more specifically and second, how they are part of the construction process.

The validation criteria are determined in relation to the purpose of the model. There are multiple ways in which we could classify different types of validation criteria. For the purposes of our framework, I distinguish between theoretical, mathematical or phenomenological criteria, which stays close to the types of criteria mentioned in Boumans (1999). Theoretical criteria include questions like: is the answer provided by the model, to some extent, in line with what we would expect from theory X? Given the law of supply of demand in economics for example, a criterion could be that the model incorporates a negative relationship between price and demand (ceteris paribus). Mathematical criteria may include criteria of analytical tractability, the model must not be so complex that it does not enhance understanding. Finally, phenomenological criteria can come in the form of empirical validation; is the model able to reproduce fact Y? Importantly, of course, all of these criteria must be relevant to the purpose of the model (Boumans, 2009). Relevance for the three types of justification criteria includes the following: First, the theoretical criteria should involve theories that have implications for the question at hand. Second, the strictness of analytical tractability criteria depends on whether the model’s purpose is to provide understanding of certain mechanisms. If a model’s purpose is solely to predict, for example, strict analytical tractability criteria are not relevant. Third, the facts to reproduce should be relevant to the explanation the model provides. If the purpose of the model is to provide an explanation of a particular phenomenon, the facts to be reproduced by the model are usually facts about that particular phenomenon. To illustrate, a model constructed to explain the business cycle in economics is usually required to be able to reproduce the empirically observed business cycle.

Models go through a process of construction. They are not just discovered, and are not a trivial extension of theory. The question is, however, whether this construction process is independent from the above described validation process. In a more traditional view, these processes are considered as independent, which roughly means that the validation process starts after the model is constructed. If the model fails to pass the validation criteria, the model is to be discarded. As shown through case studies in Boumans (1999), the problem with this traditional view is that it is not in line with actual scientific practice. Given that the validation criteria are given by the question the model is constructed to answer, they are known during the construction process, and play an important role in the construction process. Models are constructed in such a way that the model meets the criteria. When the model does not meet the criteria a “back and forth” process starts in which the model is tweaked and altered until the criteria are met to a sufficient degree. The ability of the model to meet its validation criteria is thus built into the structure of the model. This concerns all three theoretical, mathematical, and phenomenological criteria. The case studied in Boumans (1999) for example, concerns how (in addition to theoretical and mathematical criteria) a micro-founded business cycle model is constructed to reproduce the Phillips-Curve (the negative relationship between inflation and unemployment), which is a phenomenological criterion.

An additional element that may be considered, is that the ability of a model to fulfil one validation criterion is often not independent from the fulfilment of the other validation criteria. This implies that model construction, in practice, often comes down to a balancing act between the various relevant validation criteria. As an example, there may be tension between the fulfilment of theoretical and mathematical criteria. Theoretical notions may be complex to such a degree that their incorporation into a model structure would cause the model to become analytically unsolvable, or the model could become so complex that it is unintelligible. As we will see in the case study presented later, the balancing of theoretical and mathematical criteria was an explicit issue in Yule (1925). In the same way, theoretical and phenomenological criteria may be at odds. The incorporation of certain theoretical notions into a model structure may imply that the model output is not in line with certain facts about phenomena. In some instances, the modeller has to prioritize certain validation criteria. As I will discuss in more depth in the case study later in this paper, for example, the starting point for the model presented in Simon & Bonini (1958) was a dissatisfaction with microeconomic theory because of its inability to reproduce the observed distribution of firm size. Of course any balancing or prioritisation of validation criteria is again a function of the purpose of the model.

A further complicating factor may be that some validation criteria in practice cannot be identified as being purely theoretical, mathematical or phenomenological. For example, the theoretical notions that underlay what we could recognise as theoretical validation criteria, may themselves be partially based on empirical evidence. In addition, in models in physics in particular, theoretical notions are sometimes tied to particular mathematical formulations. Being able to express a theoretical notion with mathematical elegance is sometimes seen as support for that theoretical notion. Often, however, as we will also see in the case study, we are able to classify a criterion as being primarily theoretical, mathematical or phenomenological.

This account of model construction applies to model that are constructed from the ground up as well as models that re-use existing model structures. Models constructed by recycling existing model structures are also subject to the various types of criteria outlined above. For model structures to be acceptable in both the original and new domain, there must thus be overlap in the validation criteria. In the framework presented here, overlap in validation criteria are what enables model transfer across distinct domains. To clarify, we can look at the three main types of validation criteria distinguished before. In the case of theoretical criteria there may be overlap if the core idea of the theory is sufficiently abstract. We can think of certain concepts from evolutionary theory that are considered useful in biology but also in some sub-fields of economics (Dosi & Nelson, 1994). In the case of mathematical criteria, it is not hard to see that, for example, analytical-tractability criteria may apply across distinct domains. Finally, in the case of overlap in phenomenological criteria, we can think of requiring models to reproduce the same type of empirically observed distribution in the original and new domain. The account of a model template by Knuuttila & Loettgers (2016) can be seen as a vehicle for the fulfilment of theoretical and mathematical criteria. I argue that this account risks being incomplete in cases where it is overlap between phenomenological criteria enables model transfer. One may wonder how it is that certain facts about phenomena will be the same across distinct domains. In the next section, I will provide an explanation for the occurrence of overlap in phenomenological criteria.

We may posit that fulfilling these validation criteria shows some similarity relationship between the model structure and the real world structure and, in the case of model transfer, is thus evidence of a similarity relation between the targeted real world structure of the original and the new model, which is also implied by an account that looks at models as analogies such as Hesse (1966). This depends, however, on the relationship between the fulfilment of validation criteria and the representational value of the model. I argue that it is not useful to consider this relationship for the purpose of this paper. First, this relationship is complex and uncertain and depends to a large extent on whether one holds a realist or more instrumentalist stance towards scientific models (Gatti et al., 2018). Second, as is also shown in Barlas (1996) it depends on the purpose of the model. For so-called, black-box models, for example, the sole purpose of the model is to give correct predictions which implies that the representational value of the model mechanisms are not a relevant criterion of assessment. Not directly engaging with the relationship between validation criteria and the representational value of the model is thus more epistemologically neutral and covers a wider range of model-types.

3 Universal Patterns

I have stated that overlap in phenomenological criteria should be taken into account in order to come to a more complete account of model transfer. The question that remains to be answered is: when is this the case? Empirical validation tests generally consist of assessing whether the model is able to reproduce relevant facts about phenomena. Overlap of phenomenological criteria implies, therefore, that there is somehow overlap in features of these facts about phenomena. This may seem unlikely given that facts about phenomena are associated with something that is tied to empirical content, namely a phenomenon. The distribution of firm size, is about a specific domain, firms. Abstract features of such facts, however, may very well appear across multiple distinct domains. These features are what I will label as universal patterns. As we will see, the distribution of firm size follows a particular power law, the Yule distribution, which is a feature of many observed distributions in distinct domains (Simon, 1955).

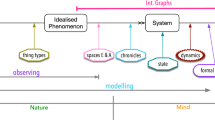
Let me first elaborate what I mean exactly by a universal pattern. A pattern can be thought of as an abstract structure. It is abstract because, by itself, the pattern does not have any empirical content, meaning that it neither empirically true or false (Humphreys, 2019). It simply does not refer to any object that can be observed empirically. It is a structure because we perceive it as something structured as opposed to being unstructured. Typical structures would be geometric shapes, like circles, curves, cycles and spirals, or it may also be structured in the sense that they can be described by a particular mathematical form. As an example of an abstract structure, we can think of patterns used in knitting; even though the patterns by themselves do not refer to anything empirical, we still recognize them as having a structure. Patterns can be made to refer to specific facts about phenomena by coupling them with specific empirical content. Empirical content, in this sense, refers to the information that relates the abstract structure to the empirically observable facts about phenomena. When the Yule Distribution is used as the distribution of genera size, for example, it is coupled with information that gives particular meaning to the shape. A point on the line that is higher than another point on the line, means that the higher point represents a genus that is larger in terms of species. Note that there are four relevant concepts within this description: the pattern, the empirical content, the fact about the phenomenon and the phenomenon itself. Patterns can be made to match a fact about a phenomenon by coupling it with empirical content. A pattern is a universal pattern if and only if it can be made to refer to facts about phenomena in multiple domains by changing just the empirical content that the pattern is coupled with. In Fig. 1, we can see a schematic overview to clarify the relationships between concepts. A single universal pattern can be made to apply both to fact about phenomenon A and B by coupling it with empirical content A and B respectively.

Fig. 1
figure 1

Universal patterns and facts about phenomena

Full size image

The notion of universal pattern put forward here is induced from the observation that certain patterns are observed and used in scientific practice in varying domains. Most straightforwardly, we can think of the Gaussian or normal distribution, which is observed across widely varying domains such as the human height or the weight of loaves of bread (Lyon, 2014). Another example are certain power distributions such as Zipf’s law (Corominas-Murtra & Sole, 2010) or the Yule distribution (Simon, 1955) which are observed in the distribution of city size and the distribution of words in a piece of literature. Universal patterns are not limited to distributions however. We can think of particular oscillation patterns for example, which are observed in (among many other domains) ecology and economics (Gandolfo, 2008).

Let me now relate the notion of universal patterns more explicitly to what we have established in the previous sections. In order for a model to be transferred across domains it must be considered useful by the practitioners in both the original and the new domain. This usefulness is considered by assessing whether the model is able to meet certain validation criteria. These validation criteria are built into the structure of the model meaning that the model structure is shaped by the criteria. For a model to be useful in a domain different from the one it was originally constructed for, the validation criteria should overlap. When phenomenological criteria have played an important role in shaping the structure of the original model, it is these criteria that should overlap in the new domain in order for the model structure to be transferred. This is the case when the phenomenological criteria embed a universal pattern.

The broad view is thus that in most modelling exercises there is a desire to latch the model onto the empirically observable world in some way. The observations we make, and the facts about phenomena we distil from them, are sometimes structured in specific ways. In such cases, models that are constructed to latch onto phenomena are likely to have a structure that is specific to that observed phenomenon. Devoid of any empirical content, such a fact about a phenomenon does not represent a universal pattern. In other instances, however, the facts about phenomena that we distil from our observations are structured in general ways. That is, they embed a pattern that can be made to refer to facts about distinct phenomena, a universal pattern. We are thus confronted with a world in which we do observe both specificity as well as generality. Where we observe specific patterns, there likely are methodological borders. Where we observe universal patterns there likely are methodological transfers. This view contributes to an explanation for the observation that some particular model structures are transferred and not others.

The notion of universal patterns that I have presented here, is related to, but different from the existing concept of universality. The field that has discussed this notion of universality most explicitly is that of statistical mechanics. In statistical mechanics, universality concerns similarities in the behaviours of diverse systems (Batterman, 2000). Another way in which this is sometimes formulated is that the system level behaviour is independent to elements of the microscopic structure system (Batterman, 2000). If this is the case, it may imply that systems constituted of different objects still show similar behaviour. An example often used is when a magnet is heated to a certain critical temperature, it will lose its magnetism (phase transition). The path between these two states as a function of temperature (coexistence curve) is described by a power function with a critical exponent close to 1/3 (Batterman, 2000). The same functional form and critical exponent is also observed in phase transitions between the fluid and vapour states of matter like that of water. Clearly, the microscopic structure of water and magnets is different. Still, some properties at a system level are strikingly similar. The same notion of universality has also been applied to systems outside of chemistry and physics, such as agent-based systems (Parunak et al., 2004) and biological systems (Batterman & Rice, 2014). The power function with a critical exponent close the 1/3 falls within the account of a universal pattern presented here. State transitions in matter and transitions in magnetism are facts about phenomena with distinct empirical content, but nonetheless express a similar pattern. The account of universal patterns that I have presented, however, does not make any statements about the relation between the observed pattern and the system it is generated by. In the statistical mechanisms notion, universality is a property of a system the behaviour of which comes in the form of widely observed patterns. This presupposes, however, that what is observed, is strictly tied to the system it is generated by. As I will discuss in the next paragraph, this limits the ways in which we can explain why we observe universal patterns, in a way that is not necessary within the context of model transfer.

Why we observe universal patterns is a fundamental question that requires a full investigation on its own and is thus beyond the scope of the main question of this paper. Generally, however we can distinguish between two types of explanations. One explanation comes from the same statistical mechanics notion discussed in the previous paragraph, and is discussed in a.o. Batterman & Rice (2014). It states that systems, even though being distinct in certain ways, still share abstract fundamental features, such as locality, conservation and symmetry. Such features provide an attractive fixed point such that systems that are different in some aspects, but share these fundamental features, converge to having the same properties, in the form of universal patterns. This explanation is related to the notion of a causal core as discussed in Lloyd (2015). The causal core consist of those features that are responsible for generating particular output, and are robust against changes that are outside this causal core. For physical systems, this explanation may seem credible, as stated before, however, universal patterns are also observed in diverse social phenomena (Simon, 1955). It might be less clear that such patterns are also the result of abstract fundamental features in the systems that they are generated by. According to some, however, this is the case. Mandelbrot & Hudson (2007), for example, applies they theory of fractals (Mandelbrot, 1982) as an explanation for the distribution of price changes on stock markets. Fractals are seen by some as a fundamental self-organizing principle of nature (Kurakin, 2011). Somehow, the code of nature is such, that distinct systems (even social ones) self-organise into similarly structured patterns. As an alternative explanation for universal patterns, we can take a more Kantian perspective and question the objective nature of the patterns we observe. As stated before, patterns are abstract structures. What we consider to be structured and unstructured may be shaped by our psychology and limited by our inability to grasp the complexity of the world. This is in line with notion from Gestalt Theory such as presented in Palmer (1999). Human psychology has a tendency to structure pieces of information into larger information structures in certain ways. The notion of universal patterns that I put forward here can be interpreted ontologically neutral. We are simply dealing with the observation that universal patterns are observed by scientists and thereby partially determine which models we consider to be useful.

4 Yule Process: a Case Study

Finally, to illustrate the account I have described above, I would like to discuss the Yule Process and the universal pattern that can be derived from it: the Yule distribution. I have chosen this example of model transfer, because there exists an explicit account of how this model has been constructed in Yule (1925) for its original context, as well as how the model structure was later used as a basis for the construction of models in other domains (Simon, 1955). More recently, the Yule Process has formed basis for many models that concern preferential attachment (Abbasi et al., 2012), which is a central notion in network theory (Newman, 2001).

4.1 Yule Process: Evolutionary Origins

George Undy Yule (1871–1951) is known as a pioneer in the field of statistics. The model that is the subject of this case study is called the Yule Process. The distribution that can be derived from this process has been labelled the Yule distribution, which is perhaps his most well-known scientific contribution (Edwards, 2001). A short history of the development of the model can be found in Bacaer (2011), on which the analysis below is partially based.

Yule developed his model in response to observations made by botanist J.C. Willis (1868–1958) in evolutionary biology. The issue concerns the distribution observed in taxonomy. Taxonomy is a biological classification scheme with a hierarchical structure in which organisms are grouped together based on common characteristics. The system is hierarchical in the sense that classifications with a so-called higher taxonomic rank are more general, and, thus, embed a classification of more specific lower taxonomic ranks. The observations made by Willis regards two such ranks, specie, and the more general rank of genus. A given genus thus contains multiple species, which have some features in common at the genus level but differ at the species level. The suborder of -Snakes-, for example, contains many more specific genera such as -Boa- which, in turn, contains the specie of -Boa Constrictor-. For several different organisms, animals and plants, Willis collected data on the number of genera that contain a given number of species. In this context, we can say that the size of a genus is determined by the number of species it contains. By tabulating this data, an interesting distribution emerged; there are many genera that contain one specie (size one), there were some larger genera, and some genera that were very large and contained more than a 100 species (size 100). What was also striking, is that this pattern appeared to emerge both in animals and plants. Yule, who was trained as a statistician under Karl Pearson, suggested to plot the data on a log-log scale. This revealed that the logarithm of the fraction of genera containing k species, \(log(p_k)\), decreased approximately linearly with log(k). This implies that there exists \(\alpha >0\) and \(\beta >0\) such that the probability density function of genera size can be written as:

$$\begin{aligned} p_k \propto \alpha k^{-\beta } \end{aligned}$$
(1)

which can be rewritten as:

$$\begin{aligned} \log {p_k} \propto \log (\alpha ) -\beta \log {k} \end{aligned}$$
(2)

In Fig. 2, I have plotted both equations for arbitrary parameters. In addition, J.C. Willis made observations regarding the age of a genus and its size. Stating that larger genera were on average older, evolutionary speaking.

Fig. 2
figure 2

Power Law for \(\alpha =0.5\) and \(\beta =1\)

Full size image

Yule was interested in providing a mathematical model, based on evolutionary theory, that was able to reproduce (1) and, in addition, to explain the observation made by Willis that the larger genera were also older. In Yule (1925) he provided this model. Yule stated the purpose of his model as follows:

The Further question arises, what is the frequency distribution, as the statistician terms it, of the sizes of these N genera which all started as monotonic genera from primordial species at zero time, after any given time has elapsed? (Yule, 1925).

This purpose encapsulated the desire to generate the distribution of genera size as well as linking genera size to evolutionary age. From the outset, there were thus some clear validation criteria, that are in line with the ones I have discussed. There was a theoretical criterion, in that the model assumptions must roughly agree with evolutionary theory, and, there was a more explicitly phenomenological criterion: the model must able to reproduce a distribution that is linear on a log-log scale.

Let us now take a look at how Yule managed to construct a model that reproduces a frequency distribution that is in agreement with these “known facts”. The two fundamental entities in this model are species and the genera they belong to. We consider how these two entities grow over time. The total number of genera is labelled as n. Each genus has a size k that is determined by the the number of species belonging to each genus at a point in time. In each time step, m species in total are added to the existing genera. After these m species have been added a new genus is added to the existing genera. This new genus starts out with \(k=1\). After this, the total number of species has thus increased by \(m+1\) (m plus the specie that is associated with the new genus). \(m+1\) new species appear for each new genus that is added, implying that the average number of species per genus is \(m+1\). With each time step n is increased by 1. This implies that the number of time steps can be represented by the total number of genera n. \(p_{k,n}\) is the fraction of genera with k species when the total number of genera is n. The total number of genera with k at n is \(np_{k,n}\). Crucial now, is the probability of a species being added to an existing genus. This probability is taken to be proportional to the size of the genus, such that, if we have a genus with \(k_i\) species the probability of a specie to be added to this genus is given by the number of species belonging to genus i over the total number of species.:

$$\begin{aligned} \frac{k_i}{n(m+1)}. \end{aligned}$$
(3)

We now have all the ingredients of the model. In short, the model consists of two main elements; constant genera growth and proportional specie growth. The question to ask is where do these ingredients come from? Part of it is a general knowledge of evolutionary theory. In the introduction to his paper, Yule discusses two opposing views regarding how evolution occurs that were relevant during his time. First, is what Yule labels as the “Darwinian view”, which assumes that differences in species and genera arise through cumulative small mutations (continuous variation) and that species necessarily die out. The “mutational view”, on the other hand, assumes that large mutations may occur “at once per saltum”, as Yule phrases it, which means with large jumps (discontinuous variation). It may seem that the type of mutation described in the model as well as the assumption that species do not die out, is more in line with Mutationalism. Yule is well known for his opposition to Mutationalism, however, which is most prominently featured in Yule (1902). In turn, to ensure that his assumptions do not disagree with the Darwinian view, Yule provides us with an explanation of how the model’s assumptions should be interpreted. First, mutations in his model are limited to “viable mutations”, such that the model does not formally contradict the dying out of species. Second, Yule points out that given a long enough time horizon, small continuous mutations accumulate to changes that may appear as discontinuous. The time horizon in the model should thus be interpreted as long enough for such small mutations to accumulate to something that would be classified as a new specie or a new genus. There was thus a clear effort to position the model within the context of existing evolutionary theory. Such considerations provide us with an example of how the ability to meet theoretical criteria are built into the structure of the model.

The model proposed by Yule, however, was certainly not a one-to-one mapping of evolutionary theory. Interestingly, behind proportional growth is the assumption that the probability of creating a new specie is the same for each individual species regardless of genus and time. This implies that larger genera will grow at a higher rate in absolute terms. Regarding this assumption, Yule states:

The assumption that the chances of specific (or generic) mutation are identical for all forms within the group considered are constant for all time are unlikely to be in accordance with the facts, but have to be made to simplify the work. (Yule, 1925).

Why did Yule make this non-factual assumption? Here we enter analytical tractability/mathematical criteria: Introducing heterogeneity in the rates at which hundreds of species and genera evolve would undoubtedly complicate the model’s computational structure, and might hamper the degree to which the model would enhance understanding. In addition, it could be that such a model can only be implemented through computer simulation, which was not a tool available to Yule. To convince the reader about the correctness of this assumption, Yule points not to evolutionary theory but to empirical facts that the model must be able to reproduce, the phenomenological criteria:

In so far as the deductions do not agree with known facts the assumptions are probably incorrect or incomplete. In so far as we find agreement, or the more nearly we find the agreement, the assumptions are probably correct. (Yule, 1925).

The model proposed by Yule indeed is able to reproduce the frequency distribution of genera:

So for as the graphic test goes, accordingly, the theory gives very well indeed precisely the form of the distribution required. (Yule, 1925).

From the outset, before any formal derivation, we can see that the constant addition of small genera, coupled with a proportional growth of species would generate a distribution with some very large genera and many smaller ones. To put it mathematically, a skewed distribution. Starting with only genera with \(k=1\), some genera, by chance, will grow slightly larger than others. These larger genera will then have a higher probability of growing even larger [(following Eq. (1)] and so on.

The description of the construction of the Yule Process shows how the model structure is shaped by a balancing act between three validation criteria: The model had to some extent be in line with notions from evolutionary theory, the model had to be solvable analytically, and the model needed to reproduce the observed statistical distribution. It it these criteria that served as the standards for model usefulness to Yule. This shows that the Yule Process is a model that was constructed for a specific domain and the structure is shaped by the validation criteria within this domain.

4.2 The Yule Process as a Model for Firm Growth

How was the structure of the Yule Process, used as a basis for the construction of models in other domains? In the analysis we have established that overlap in validation criteria between domains is necessary for models to be useful in multiple domains. Let us look, therefore, at which considerations were most important in the selection of the Yule Process as a basis for constructing models in a new domain.

The Yule Process has been used to model processes of many different subjects (Simon, 1955). As an example, we will look at how the Yule Process was first applied to model the distribution of firm size in Simon & Bonini (1958). Let me first provide a little background of the scientific discussions regarding models of firm size at the time of Simon & Bonini (1958). At that time, it had long been observed that the distribution of firm size is heavily skewed (Gibrat, 1931), implying a distribution in which there are some very large firms and many smaller firms. The non-normality of this distribution was seen as evidence of the non-trivial nature of the growth process. The observation brought with it, a dissatisfaction of standard economic theory because it was unable to make predictions regarding the distribution of firm size (Simon & Bonini, 1958). Born from this dissatisfaction, the goal in Simon & Bonini (1958) was to provide a model that was able to generate the observed distribution of firm size. From the start, the model construction was thus aimed at a phenomenological criterion.

Simon & Bonini (1958) starts with the assertion that in order to generate the distribution of the type observed in firm size, the law of proportional effect is an essential ingredient for the model. The law of proportional effect was first introduced by Gibrat (1931) and entails that growth is proportional to size. It is the same structure labelled by Yule as proportional growth. In the case of firms, this would mean that the same percentage of growth rates applies to firms of different sizes. This implies that larger firms grow faster in absolute terms. Concretely, this means that the expected percentage return on investments is not a function of firm size. Computationally, this is in line with growth in the original Yule process, in which larger genera will grow at higher absolute rates as well. This, however, was not enough to narrow down the appropriate model to one. Simon & Bonini (1958) states that there may be multiple distinct growth processes (model structures) that will generate the type of distribution skewness observed empirically as long as proportional growth is incorporated:

If we incorporate the law of proportionate effect in the transition matrix of a stochastic process, then, for any reasonable range of assumptions, the resulting steady-state distribution of the process will be a highly skewed distribution, much like the skewed distribution of that have been so often observed for economic variates. In fact, by introducing some simple variations into the assumptions of the stochastic model - but retaining the law of proportionate effect as a central feature of it - we can generate the log-normal distribution, the Pareto distribution, the Yule distribution, Fisher’s log distribution and others - all bearing a family resemblance through their skewness. (Simon & Bonini, 1958).

Proportional growth was thus deemed as essential for generating the type of distribution that was observed for the size of firms. This still left open, however, a range of skewed distributions and processes that generate them. In order to narrow down the growth process further, Simon & Bonini (1958) looked more closely to the characteristics of the observed distribution of firm size.

The log-normal function has most often been fitted to the data and generally fits quite well. It has usually been noticed, however, that the observed frequencies exceed the theoretical in the upper tail and that the Pareto distribution fits better than the log-normal in that region. The observation suggests that the stochastic mechanisms proposed in the previous section are the appropriate ones and that the data should be fitted with the Yule Distribution. (Simon & Bonini, 1958).

The observed pattern is thus one of a particular shape: it is log-normal except for the upper tail which is Pareto distributed. These two characteristics are consistent with the pattern of the Yule distribution. In order to reproduce this pattern, Simon & Bonini (1958) incorporates the second essential ingredient of the Yule Process; constant entry of new small firms. In this way Simon & Bonini (1958) arrives at a model which has the same structure as the the original model and is able to meet the validation criteria within the new domain.

4.3 Overlapping Validation Criteria

Where can we find overlap in the validation criteria between the original and new domain? First, if we look at theoretical criteria, we do not see strong indications of overlap. The evolutionary theory that served as a criterion in the original construction of the Yule Process did not play an explicit role when the model structure was applied to firms. In Simon & Bonini (1958) we see that theoretical criteria did not seem to play a big role altogether. Rather, Simon & Bonini (1958) is partially born out of a dissatisfaction with the inability of microeconomic theory to explain empirical patterns. Second, for both models there was an, at least implicit, mathematical criterion of analytical tractability. The Yule Process was a good candidate because the model structure was shown by Yule (1925) to fulfil this criterion. In line with Knuuttila & Loettgers (2020), this criterion is fulfilled by countless model structures and is not enough to narrow things down to a particular model structure. By itself, it is not a complete explanation as to why the Yule Process was transferred to the new domain. Third, is the overlap between the pattern observed in the distribution of genera size and the pattern observed in the distribution of firm size. It was this pattern, a certain shape, that enabled the model structure of the Yule Process to be considered as useful in both domains.

5 Conclusion

What explains inter-domain model transfer in science? I have put forward an account of model transfer that starts from the construction process of models in practice. In practice, models are constructed such that they meet relevant validation criteria. These criteria can be theoretical, mathematical or phenomenological in nature. The structure of the models is shaped by these criteria. In this sense, a model structure can thus be seen as an artefact that meets certain criteria. If such criteria are domain specific, the model structure will only transfer within the original domain of construction. If, however, the validation criteria also apply to other domains to a large enough extent, the model structure may be considered a useful tool in these domains as well. Inter-domain overlap in theoretical criteria applies in cases where the core of the theory in question is sufficiently abstract, such as complexity science. Mathematical criteria play an important role in shaping many model structures and these criteria will often overlap between domains, analytical tractability, for example. I agree with Knuuttila & Loettgers (2020), however, that such criteria are in some sense so general that they to not constitute a complete explanation. They do not explain the fact that some particular model structures are transferred and others are not. Phenomenological criteria, in the form of an ability to reproduce certain patterns may overlap across domains if the pattern in universal. Universal patterns are abstract structures that can be fitted to facts about phenomena in multiple domains by coupling it with domain-specific empirical content. Why we observe such patterns in an ontological question which may tell us something about how nature self-organises into typical structures, or may tell us something about our way of dealing with the limitations of grasping nature’s complexity.

The case of the Yule process provides us with evidence that universal patterns are what enables model transfer in some instances. The case shows how the Yule distribution shaped the original Yule Process model to a large degree. Stripped from its ontological content, the Yule Process is a device that generates a specific pattern in an analytically tractable way. The reason why Simon & Bonini (1958) uses the same model structure to constructed a model of firm growth is clear; the model structure was able to reproduce a specific pattern. It was this phenomenological validation criterion that enabled the model transfer. Importantly, the pattern is the starting point for Simon & Bonini (1958), and not the way in which the mechanisms of the model, proportional growth and constant addition of new entities, could be made to apply to firms instead of genera.

The Yule Process case study, presents us with an instance in which overlap in phenomenological criteria was the primary reason that the particular model structure of the Yule Process was transferred between domains. It is important to state, however, that in other cases (for example Knuuttila & Loettgers (2020)), the primary reason for model transfer may overlap in theoretical and/or mathematical criteria.

The added value of the account presented in this paper is threefold. First, instead of starting from a particular epistemological view regarding what makes models useful, it starts from looking at how models are constructed in practice. In practice, it is the validation process that determines when a model is considered to be useful. The account is, therefore, neutral in the sense that is open to a multitude of epistemological viewpoints. Whether we consider models to be close representations of the reality or more akin to measurement instruments, for example, ultimately depends on what it means that a model fulfils certain validation criteria. Second, by introducing the notion of overlap in phenomenological criteria as an enabling source of model transfer in addition to analytical tractability and theoretical concepts, the account in this paper extends the account of the model template Knuuttila & Loettgers (2016) to apply to a wider variety of model transfer cases. Third, it provides a concept that answers to some degree why overlap in phenomenological criteria may occur or even be prevalent, namely universal patterns.