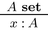Abstract
In the present paper, the Fregean conception of proof-theoretic semantics that I developed elsewhere will be revised so as to better reflect the different roles played by open and closed derivations. I will argue that such a conception can deliver a semantic analysis of languages containing paradoxical expressions provided some of its basic tenets are liberalized. In particular, the notion of function underlying the Brouwer–Heyting–Kolmogorov explanation of implication should be understood as admitting functions to be partial. As argued in previous work, the correctness of an inference rule (and of a hypothetical derivation) should not be defined in terms of transmission of provability, but rather should be grounded on weaker principles, which I show that are motivated by consideration about the content of the inversion principle. In the conclusion, I briefly address the issue of compositionality, arguing that the violation of compositionality induced by paradoxes are no worse than others that are regarded, at least by Dummett, as wholly unproblematic.
Similar content being viewed by others
Notes
Thus Frege’s terminology, according to which functions and objects are unsaturated and saturated entities respectively, is reversed in the context of intuitionistic type theory: dependent objects are unsaturated entities and the functions proving \(A\supset B\) are saturated entities.
In rule schemata, square brackets are used to indicate the form of the assumptions that can be discharged by rule applications. On the other hand, in schematic derivations, a formula in square brackets indicates an arbitrary number (\(\ge 0\)) of occurrences of that formula, if the formula is in assumption position, or of the whole sub-derivation having the formula in brackets as conclusion, as done by Prawitz (1965). Moreover, following Prawitz I indicate discharge in actual (respectively schematic) derivations simply with numbers (resp. possibly indexed letters) placed above the discharged assumptions and to the left of the inference line at which the assumptions are discharged.
We use A(t / x) for capture-avoiding substitution of t for x in A.
When we apply “open” and “closed” to the sub-derivation \(\mathscr {D}'\) of a given derivation \(\mathscr {D}\) we will however consider \(\mathscr {D}'\) to be open if on the path between its conclusion and the conclusion of the whole derivation \(\mathscr {D}\) one encounters a rule application that could discharge assumptions in \(\mathscr {D}'\). Thus the immediated sub-derivation of a derivation ending with \(\supset\)I will always be considered open, even if the application of \(\supset\)I the discharge is vacuous and all assumptions were already discharged.
The term fully evaluated is from Nordström et al. (1990). In Tranchini (2012, 2016a), I put more emphasis on the notion of normal derivation rather than of fully evaluated derivation. That fully evaluated derivations, and not normal derivations, should be regarded as those denoting proofs in the most direct way is a significant shift of perspective compared to previous formulations of proof-theoretic semantic that I gave, as it will clearly emerge in Sect. 5 below. I thank one of the referee for forcing me to clarify this point.
As observed by one of the referees, in denotation semantics for the untyped lambda calculus (stemming from Scott 1970; Scott and Strachey 1971), one usually identifies denoting terms with solvable terms rather than with normalising terms, where the solvable terms can be syntactically characterized as those that reduce to head normal form (Barendregt 1985, Chap. 8). As fully evaluated derivations are essentially those in weak head normal form, our proposal can be seen as equating denoting derivations with weakly solvable terms (Abramsky and Ong 1993). A systematic investigation of these connections is left for further work.
It should be observed that in intuitionistic type theory one is entitled to assume x : A only if one has previously established that A is a well-formed sentence, which is expressed in the theory by a third form of judgement, \(A\ \mathbf {set}\). We thus have the following rule for introducing assumptions in derivations:
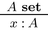
Judgements of the form \(A\ \mathbf {set}\) must in turn be derived by means of a fourth kind of rules beside introduction, elimination and equality rules, called formation rule. Moreover, implicit in each introduction, elimination and equality rules are also opportune premises having this form. For the present purposes we can however avoid these complications.
These considerations justify in fact the elimination rules having the form first proposed by Martin-Löf (1972) and Prawitz (1979) and later generalized by Schroeder-Heister (1981, 1984). The “direct” elimination rules discussed in the paper are equivalent with those in general form in the framework of Gentzen-Prawitz natural deduction, but in a type-theoretic setting the general rules are strictly stronger (Garner 2009).
Non-standard elements are of course ruled out by the second-order definition (“The set of natural numbers is the smallest set X such that...”) which is however strictly stronger than the first-order formulations given by clauses (i)–(iii) or encoded by the introduction and elimination rules. The second order-formulation is categorical, while the first-oder formulations aren’t!
Moreover they do rule out certain rules as incorrect, for instance those of \(\mathsf {tonk}\), for a thorough discussion see Tranchini (2016a).
As a matter of fact, the following definition could be strengthened by requiring that the collection of elimination rules for \(\dagger\) should be at least interderivable with the unique elimination rule in general form. For the need of an even stronger condition see Tranchini (2016b).
We consider only reductions, neither expansions nor permutations.
These slight changes with respect to Prawitz’s original definitions (Prawitz 1971, 1973, 1974, see) are not intended to make the notion of validity applicable only to derivations in a formal system whose set of rules is fixed in advance. On the contrary as the clause for the validity of open derivations makes clear, the system considered can be extended by means of further primitive symbols, provided that they are governed by introduction rules (satisfying the complexity condition) and elimination rules (satisfying the mild requirement discussed in Sect. 1).
For which sub-derivations count as closed cf. footnote 4.
The validity of such a derivation seems to be the most direct counterpart in the typed setting of the weakly solvability of \(\lambda y. \mathtt {app}(\lambda x.\mathtt {app}(x, x)\ ,\ \lambda x.\mathtt {app}(x, x))\) (see Abramsky and Ong 1993, §1.1 and §2.3).
References
Abramsky S, Ong C (1993) Full abstraction in the lazy lambda calculus. Inf Comput 105(2):159–267
Barendregt H (1985) The Lambda Calculus – its syntax and semantics, vol. 103 of Studies in Logic and the Foundations of Mathematics. Elsevier, Amsterdam
Dummett M (1981) Frege. Philosophy of language, 2nd edn. Duckworth, London
Garner R (2009) On the strength of dependent products in the type theory of Martin-Löf. Ann Pure Appl Logic 160(1):1–12
Martin-Löf P (1971) Hauptsatz for the intuitionistic theory of iterated inductive definitions. In: Fenstad J (ed) Proceedings of the second Scandinavian logic symposium, vol. 63 of Studies in Logic and the Foundations of Mathematics. Elsevier, Amsterdam, pp 179–216
Martin-Löf P (1972) An intuitionistic theory of types. In: Sambin G, Smith J (eds) Twenty-five years of constructive type theory. Oxford University Press, Oxford
Martin-Löf P (1975) About models for intuitionistic type theories and the notion of definitional equality. In: Kanger S (ed) Proceedings of the third Scandinavian logic symposium, vol. 82 of Studies in Logic and the Foundations of Mathematics. Elsevier, Amsterdam, pp 81–109
Martin-Löf P (1984) Intuitionistic type theory. Bibliopolis, Napoli
Nordström B, Petersson K, Smith JM (1990) Programming in Martin-Löf’s type theory. An introduction. Oxford University Press, Oxford
Prawitz D (1965) Natural deduction. A proof-theoretical study. Almqvist & Wiksell, Stockholm. Reprinted in 2006 for Dover Publication
Prawitz D (1971) Ideas and results in proof theory. In: Fenstad J (ed) Proceedings of the second Scandinavian logic symposium, vol. 63 of Studies in Logic and the Foundations of Mathematics. Elsevier, Amsterdam, pp 235–307
Prawitz D (1973) Towards a foundation of a general proof theory. In: Suppes P, Henkin L, Joja A, Moisil GC (eds) Proceedings of the fourth international congress for Logic, Methodology and Philosophy of Science, Bucharest, 1971, vol. 74 of Studies in Logic and the Foundations of Mathematics. Elsevier, Amsterdam, pp 225–250
Prawitz D (1974) On the idea of a general proof theory. Synthese 27:63–77
Prawitz D (1979) Proofs and the meaning and completeness of the logical constants. In: Hintikka J, Niiniluoto I, Saarinen E (eds) Essays on mathematical and philosophical logic: proceedings of the fourth Scandinavian logic symposium and the first Soviet-Finnish logic conference, Jyväskylä, Finland, June 29–July 6, 1976, Kluwer, Dordrecht, pp 25–40
Prawitz D (2012) The epistemic significance of valid inference. Synthese 187(3):887–898
Read S (2010) General-elimination harmony and the meaning of the logical constants. J Philos Logic 39:557–76
Schroeder-Heister P (1981) Untersuchungen zur regellogischen Deutung von Aussagenverknüpfungen, PhD thesis, Bonn University
Schroeder-Heister P (1984) A natural extension of natural deduction. J Symb Logic 49(4):1284–1300
Schroeder-Heister P (2006) Validity concepts in proof-theoretic semantics. Synthese 148:525–571
Schroeder-Heister P (2012) Proof-theoretic semantics, self-contradiction, and the format of deductive reasoning. Topoi 31(1):77–85
Schroeder-Heister P, Tranchini L (2017) Ekman’s paradox. Notre Dame J Formal Log 58(4):567–581
Scott D (1970) Outline of a mathematical theory of computation, Technical Report PRG02, OUCL
Scott D, Strachey C (1971) Toward a mathematical semantics for computer languages, Technical Report PRG06, OUCL
Sundholm G (2006) Semantic values for natural deduction derivations. Synthese 148:623–638
Sundholm G (2012) “Inference versus consequence” revisited: inference, consequence, conditional, implication. Synthese 187:943–956
Tennant N (1982) Proof and paradox. Dialectica 36:265–96
Tranchini L (2012) Truth from a proof-theoretic perspective. Topoi 31(1):47–57
Tranchini L (2015) Harmonising harmony. Rev Symb Log 8(3):411–423
Tranchini L (2016a) Proof-theoretic semantics, paradoxes, and the distinction between sense and denotation. J Log comput 26(2):495–512
Tranchini L (2016b) Proof-theoretic harmony: towards an intensional account. Synthese. https://doi.org/10.1007/s11229-016-1200-3
Troelstra A, van Dalen D (1988) Constructivism in mathematics. An introduction (I), vol. 121 of Studies in Logic and the Foundations of Mathematics. Elsevier, Amsterdam
Acknowledgements
I thank Gabriella Crocco and Antonio Piccolomini d′Aragona for inviting me to the workshop “Inference and Proofs” in Marseille and to contribute to the present volume. Different versions of this paper have been presented at the workshop on “Logical Consequence”, held at the Universidad de Navarra in May 2016 and at the Logic Colloquium in Konstanz in fall 2017. I wish to thank the organizers and the participants for their comments and remarks. Thanks to Ansten Klev for helpful comments on a previous version of the paper. Finally I thank the referees for their very insightful comments on a previous version of the paper. This work has been financed by the Deutsche Forschungsgemeinschaft as part of the project “Logical Consequence and Paradoxical Reasoning” (Tr1112/3-1), by the Deutsche Forschungsgemeinschaft and the Agence Nationale de la Recherche as part of the project “Beyond Logic” (Schr 275/17-1) and by the Ministerio de Economía, Industria y Competitividad, Government of Spain as part of the project “Logic and Substructurality” (FFI2017-84805-P).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The author declares that he has no conflict of interest.
Ethical Approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Rights and permissions
About this article
Cite this article
Tranchini, L. Proof, Meaning and Paradox: Some Remarks. Topoi 38, 591–603 (2019). https://doi.org/10.1007/s11245-018-9552-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11245-018-9552-6