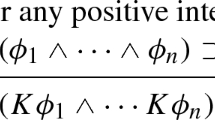Abstract
The paper critically discusses two prominent arguments against closure principles for knowledge. The first one is the “argument from aggregation”, claiming that closure under conjunction has the consequence that, if one individually knows i premises, one also knows their i-fold conjunction—yet, every one of the premises might exhibit interesting positive epistemic properties while the i-fold conjunction might fail to do so. The second one is the “argument from concatenation”, claiming that closure under entailment has the consequence that, if one knows a premise, one also knows each of its remote consequences one arrives at—yet, again, the premise might exhibit interesting positive epistemic properties while some of its remote consequences might fail to do so. The paper firstly observes that the ways in which these two arguments try to establish that the relevant closure principle has the relevant problematic consequence are strikingly similar. They both crucially involve showing that, given the features of the case, the relevant closure principle acts in effect as a soritical principle, which is in turn assumed to lead validly to the relevant problematic consequence. There are however nontransitive logics of vagueness (“tolerant logics”, developed elsewhere by the author) where soritical principles do not have any problematic consequence. Assuming that one of these logics is the correct logic of vagueness, the paper secondly observes that both arguments describe situations where knowledge is arguably vague in the relevant respects, so that a tolerant logic should be used in reasoning about it, with the effect that the relevant soritical principle no longer validly leads to the relevant problematic consequence. This shows an interesting respect in which the gap between validity and good inference that arguably arises in a transitive framework can be bridged in a tolerant one, thereby approximating better certain features of our epistemic lives as finite subjects. Moreover, even for those who do not subscribe to tolerant logics, the paper’s two observations jointly indicate that, for all the arguments from aggregation and concatenation show, the status of the relevant closure principles should be no worse than that assigned by one’s favoured theory of vagueness to soritical principles, which only rarely is plain falsity and can indeed get arbitrarily close to full truth.
Similar content being viewed by others
Notes
In the context of this paper, ‘Sp.’ admits of several reasonable interpretations: “Sorites paradox”, “species”, “spurious”.
Traditional deviations from classical logic (such as e.g. intuitionist logic) only weaken the operational properties of the logic—that is, roughly, those properties that concern particular logical operations expressible in the language (for example, reductio is an operational property in that it concerns negation). Structural properties of the logic are instead, roughly, those properties that concern the consequence relation itself, independently of which logical operations are expressible in the language. In addition to transitivity, which is about to be introduced in the main text and which will be the focus of this paper, another prominent example is contraction, according to which, if \(\Gamma , \varphi , \varphi \vdash \psi \) holds, \(\Gamma , \varphi \vdash \psi \) holds. Indeed, one might interpret the multiple uses of (3) made in Sp. Baldness as appealing to contraction, and, in fact, I briefly develop a noncontractive solution to the Sorites paradox in Zardini (2019c), for then arguing however that it is multiply inferior to a nontransitive one (see Zardini (2019a) for a specific philosophical justification of noncontractive logics, Zardini (2015b) for an in-depth treatment of nontransitive logics and Zardini (2018) for a brief general overview of philosophical applications of substructural logics).
A bit more explicitly, for example, the intermediate conclusion that a man with 3 hairs is bald follows immediately by modus ponens only from (3) and the premise that a man with 2 hairs is bald. (Well, that’s not really true since universal instantiation must first be applied to (3). However, for the reasons indicated in Zardini (2019c), we can henceforth safely ignore that intermediate step.) That in itself is harmless—the paradox gets going only by inferring from it that that intermediate conclusion already follows simply from (3) and (1). The inference is justified by observing that the premise that a man with 2 hairs is bald is actually a lemma, in that it can in turn be derived from (3) and (1), so that everything that follows from such a premise (together with (3)) can be taken to follow already simply from (3) and (1). More abstractly, the principle appealed to here is something like the principle that, if \(\Gamma _{1} \vdash \varphi \) holds and, for some \(\Gamma _{2} \subseteq \Gamma _{1}\), \(\Gamma _{2}, \varphi \vdash \psi \) holds, \(\Gamma _{1} \vdash \psi \) holds (let \(\Gamma _{1}\) be \(\{(1),(3)\}\), let \(\varphi \) be ‘A man with 2 hairs is bald’, let \(\Gamma _{2}\) be \(\{ (3)\}\) and let \(\psi \) be ‘A man with 3 hairs is bald’), a version of transitivity of logical consequence.
Since transitivity might fail in a logic without failing for arguments of the form of Sp. Baldness (and so without [failing so that (1), (2) and (3) are no longer inconsistent]), that already suffices for showing that not every nontransitive logic is a tolerant logic (while of course every tolerant logic is a nontransitive logic).
Much less importantly for the purposes of this paper (fn 14), on the quantitative side, “bounded” roughly in the sense that we are not able to handle directly each member of a set of e.g. googol-many propositions (see Zardini (2015a), pp. 513–520 for the exact sense of this kind of claim). Much more importantly for the purposes of this paper, on the qualitative side, “imperfect” in the sense that even our handling of a single proposition typically has some flaw or other. I’ll henceforth use ‘finite’ and its relatives as a catch-all phrase for the totality of these and the other negative aspects of our earth-born epistemic existence. Such finitude, as we’ll see, does surround us with shadows even qua denizens of the logical realm: even there, videmus per speculum et in aenigmate. What kind of logic is most appropriate for vision under such conditions?
I understand the “preservation” in question in the sense that (the argument the inference corresponds to is valid and), if one knows that the argument the inference corresponds to is valid, then, if one knows the premises, one knows the conclusion, where in turn I understand the more embedded implication as a material implication. I’ll briefly mention in fn 45 an alternative understanding of “good” inferences. Thanks to Pedro Dinis for eliciting these clarifications.
Although, in this paper, the main focus is, roughly, closure of knowledge under logical consequence, we’ll also see a couple of cases where what is supposed to be closed under logical consequence is something different from knowledge (Sect. 2.2) or what knowledge is supposed to be closed under is something different from logical consequence (Sect. 3.2): those cases indicate that the dialectic of the paper has a range of applicability that goes beyond closure of knowledge under logical consequence. Throughout, unqualified talk of ‘closure’ and its relatives is meant to express such an open-ended range. Thanks to an anonymous referee for an observation that led to this clarification.
Throughout, impersonal ‘know’ and its relatives are implicitly understood as relative to the relevant epistemic subjects.
For example, the kind of formulation just considered in the main text—in addition to having a much more restricted scope than the idea of closure in that it only concerns propositions believed exclusively in virtue of the relevant inference—blatantly suffers from the problem that the conclusion may be believed purely in virtue of a competent inference from the premises but in a deviant way (see Chisholm (1966), p. 30 for the introduction of the problem of deviant causal chains, and Zardini (2018), p. 263, fn 13 for its extension to deviant rational chains).
One point (which I first made in the 2009 course mentioned in the acknowledgements) to counterexample them all: one can have a defeater for one’s knowledge of the conclusion that does not also defeat one’s knowledge of the premises and of the entailment (nor the competence of one’s inference). For example, a world authority on disjunction might mischievously have told one that there are certain important features of disjunction one might not be sensitive to when believing a disjunctive proposition. One knows that snow is white and that the proposition that snow is white entails the proposition that snow is white or grass is blue, and one competently infers the conclusion that snow is white or grass is blue believing it purely in virtue of a competent inference from the premise blah blah blah—but one is still not in a position to know it. You might of course try to take this point into account and chisholm the formulation of closure with the addition of some sort of no-undefeated-defeaters clause (hello Lehrer and Paxson 1969). However, I think that, by now, we’ve got ample grounds to expect that there is no exceptionless, nontrivial and adequately strong formulation of closure, simply because such a formulation would require an exceptionless, nontrivial and adequately weak sufficient condition for knowledge (in the restricted case where the proposition to be known is the conclusion of a valid argument all of whose premises are known)—and such sufficiency is exactly where a significant part of the post-Gettier attempts at analysing knowledge foundered (see Shope (1983) for an indicative survey).
Throughout, ‘\(\langle \varphi \rangle \)’ is a singular term referring to the proposition expressed by the sentence \(\varphi \).
The restriction to finitely many premises is there only for the sake of simplicity. Some might think that valid arguments with essentially infinitely many premises present distinctive obstacles to closure of knowledge, but I think that, once we distinguish sharply between knowledge that P and mere knowledge of a method that, possibly unbeknown to the subject, establishes that P, and reflect that it is only the latter that infinity cases arguably show not to be closed (assuming the truth of e.g. Goldbach’s Conjecture, think of all its instances), we can see that no such obstacle exists (see Zardini (2015a), pp. 513–520 on cognitive aspects of arguments with essentially infinitely many premises).
Closure of knowledge under logical consequence (whether known or not) is a bit of a mixed-up principle, since, while the primary bearers of logical consequence are arguably sentences (Zardini 2019g), those are arguably not the primary bearers of knowledge (obvious). A natural fix would be to talk about knowledge of the proposition expressed by a sentence in the subject’s context, but even such a fix is actually problematic in the presence of context dependence (as per the considerations put forth in another setting by Zardini (2012b), pp. 260–266), not to speak of the fix consisting in disquoting from logical consequence to knowledge (among other things, as per the considerations put forth in another setting by Zardini (2012b), pp. 256–266). My favoured fix, as realised in (CLOS), relies instead on the plausible assumption that there is a notion of proposition under which propositions can serve as derivative bearers of logical consequence. (Sometimes, the opposite—and more discriminating—fix relying on the plausible assumption that there is a notion of sentence under which sentences can serve as derivative bearers of knowledge is also helpful in diagnosing and treating certain seeming problems arising from formulations of closure of knowledge under logical consequence that do not pay heed to the divergence between the primary bearers of logical consequence and the primary bearers of knowledge. For example, it seems that one can know both that wine is made with grapes and that wine is alcoholic while believing for whatever reasons that the two occurrences of ‘wine’ in ‘Wine is made with grapes’ and ‘Wine is alcoholic’ refer to different substances, and so possibly without being in a position to know that something made with grapes is alcoholic; given the plausible assumption that facts of de iure and de facto coreference are realised at some level of syntactic representation, this can naturally be accounted for by one’s knowing both something like ‘\(\hbox {Wine}_{{i}}\) is made with grapes’ and something like ‘\(\hbox {Wine}_{{j}}\) is alcoholic’ (but not something like ‘\(\hbox {Wine}_{{i}}\) is alcoholic’), from which (as opposed to, say, ‘\(\hbox {Wine}_{{i}}\) is made with grapes’ and ‘\(\hbox {Wine}_{{i}}\) is alcoholic’) ‘Something made with grapes is alcoholic’ does not follow, thereby avoiding a counterexample to the relevant sentence-based formulation of closure of knowledge under logical consequence.) Having said this, I note that, throughout, in my own presentation, I’m actually cavalier in my talk about the bearers of logical consequence and the bearers of knowledge, focusing in every context on the presentationally most natural kind of bearer.
Roughly, (CLOS) fails for a “boring” reason if it fails because of psychological limitations or nonnormal epistemic features (such as those exploited in fn 10). All the arguments against (\(\mathrm {CLOS}\)) I’ll focus on in the bulk of this paper are arguments on which (\(\mathrm {CLOS}\)) would fail not for a “boring” reason (but because of the very normal imperfection of our epistemic lives). Correspondingly, under the assumption that knowledge requires belief, I’ll henceforth presuppose that the relevant epistemic subjects always form the beliefs that, under suitable idealisations, they might be in a position knowledgeably to form (otherwise, (CLOS) and quite a few other interesting claims to be considered in this paper would fail for “boring” reasons). I believe that making such a presupposition is more insightful than switching from closure of knowing to closure of being in a position to know, since, on typical understandings of what it is to be in a position to know, failure to know what one is in a position to know determines the general phenomenon that, because of such failure, one may be in a position to know—or, sometimes, even know—certain propositions that entail propositions one is not only not in a position to know, but also cannot even possibly know (Zardini 2015c, pp. 383–385; 2016, pp. 468–470). A species of the phenomenon is given by the fact that one may be in a position to know each of two propositions one of which—by describing one’s failure to know what one is in a position to know—clashes with one’s knowing the other one (see Fitch (1963) for a celebrated example); another species of the phenomenon is given by the fact that one may know a proposition which—by describing one’s failure to know what one is in a position to know—clashes with one’s knowing one of its consequences (for example, one may know that one does not know any disjunctive proposition, but, under the standard assumption that one satisfies the relevant instances of (M), (C) and (N) (to be introduced in the next paragraph), one cannot possibly know that [one does not know any disjunctive proposition or it is not the case that, if grass is green, grass is green], even though one knows that \(\langle \)One does not know any disjunctive proposition\(\rangle \) entails \(\langle \)One does not know any disjunctive proposition or it is not the case that, if grass is green, grass is green\(\rangle \)). Thanks to Patrick Greenough for interesting discussions on “boring” reasons.
At least assuming a modicum of logical knowledge, so that, if one knows that \(\langle P_{1}\rangle , \langle P_{2}\rangle , \langle P_{3}\rangle \ldots , \langle P_i\rangle \) entail \(\langle Q\rangle \), [for every \(j < i\), one knows that \(\langle P_{1}\) and \(P_{2}\) and \(P_{3}\ldots \) and \(P_{j}\rangle \) and \(\langle P_{j+1}\rangle \) entail \(\langle P_{1}\) and \(P_{2}\) and \(P_{3}\) ... and \(P_j\) and \(P_{j+1}\rangle ]\) and one knows that \(\langle P_{1}\) and \(P_{2}\) and \(P_{3}\) ... and \(P_{i}\rangle \) entails \(\langle Q\rangle \)...
... and at least assuming classical logic in the metatheory. One of the main points I’ll be making in Sect. 2 is that, once we assume instead a suitable tolerant logic in the metatheory, (M), (C) and (N) no longer entail (\(\mathrm {CLOS}\)) (in particular, (C) becomes too weak to do its intended job in securing the putative entailment). Thanks to Sven Rosenkranz for originating this clarification.
Throughout, the “close kin”-relation is as follows: the formal principles are got by deleting the first occurrence of ‘one knows that’ in the principles of this paper and by adding ‘the following sentence is a logical truth:’ at the beginning of their main consequent.
Not quite. The original idea of closure was that logical consequence is in principle transparent for knowledge (a medium through which the light of knowledge can in principle propagate). That idea concerns the preservation of knowledge (from the premises to the conclusion), but (N) concerns instead the generation of knowledge (of a logical truth). In general, it is not at all clear that a method good enough to yield knowledge as output when fed knowledge as input is also good enough to yield knowledge as output when fed no input (if anything, it is the converse implication that would seem more clearly the case). Therefore, while the original idea of closure is plausibly understood as comprising both (M) and (C), (N) is plausibly better understood as an afterthought combining with the original idea of closure to yield a beefed-up idea of closure. To keep things simple, and probably contrary to prevalent use with schematic notation, assuming that logical truths follow “ex nihilo” (CLOS) is in this paper officially so understood as to include (N) as a limit case, and so as to capture the beefed-up idea of closure rather than the original one. (I leave it as an exercise to the interested reader to find a formulation of (CLOS) that, under the same assumption, is more straightforwardly understood to include (N) as a limit case. Hint: consider collections of premises and exploit vacuous restricted quantification over their members.) However, arguably, that assumption is a \(\hbox {XX}\)th-century myth (Zardini 2018, p. 269, fn 34), so that, arguably, when all is said and done (not in this paper), (CLOS) and (N) should be kept essentially distinct, with the former in itself capturing the original idea of closure and only in combination with the latter capturing the beefed-up one. This is of course not to deny that, at least in a nonrelevant logic (where anything entails every logical truth), even when all is said and done, (CLOS) and the assumption that one knows something (and knows that the logic is nonrelevant) together entail (N) (just like the original idea of closure and the assumption that one knows something together entail the beefed-up idea of closure). But analysis cannot take for granted nonrelevance or antiscepticism.
Typically, traditional epistemology does not even mention an alleged principle of “no-premise closure” (related to (N)), presumably on the strength of something like the considerations marshalled in fn 18. Obviously, traditional epistemology does amply discuss our knowledge of logical truths, but the focus is fundamentally inverted with respect to the one of discussions of (M) and (C): to wit, the discussion is almost always about how we know them (see Dodd and Zardini (2019) for a recent collection), not about whether we can in principle know them (a rare challenge to (N) on which it would fail for a not “boring” reason is offered by Sorensen (2002), pp. 545–553, but the challenge relies on a view on the Knower paradox that I for one would reject, see Zardini (2019h)).
Having noted such interesting convergence, I should add that the logical focus on certain principles makes less sense from a philosophical point of view. Firstly, modal logic typically gives a pivotal role to the close kin of:
- \((\mathrm {E})\):
-
If one knows that \(\langle P\rangle \) and \(\langle Q\rangle \) are equivalent, one knows that P iff one knows that Q,
which makes pieces of knowledge of equivalent propositions equivalent. But, while, because of its relative weakness with respect to (M), (E) might be interesting for other applications of modal logic (for example, for a logic of discovery, since obviously discovery does not satisfy (M) but might still satisfy (E)), it would not seem terribly interesting for the case of knowledge, since typical arguments against (M) (including the one to be discussed in Sect. 3, though neither in that case nor in similar ones will I bother to make this explicit) are just as good arguments against (E) too (e.g. by taking as conclusion the conjunction of the premise with the original conclusion). I mean this claim to include the [heavy-weight]-conclusion argument against (M) (Dretske 1970), given the platitude that, if one (is so uneducated concerning the respective looks of zebras and mules so that one) does not know that the animal in front is not a cleverly disguised mule, one does not know that [it is a zebra and not a cleverly disguised mule] either. It’s true that the main approaches that take that argument to establish that (M) fails account for this failure in a way that does not imply failure of (E) (see e.g. the sensitivity-based approach of Nozick (1981), pp. 167–288), but, given the platitude just mentioned, that would seem a problem for such accounts rather than evidence for the interest of (E) for the case of knowledge. Secondly, (K) is a mash-up: in itself, it’s just closure of knowledge under modus ponens (and why on earth should modus ponens be bestowed such a privileged status vis-à-vis every other valid argument?), but, by relying on the implicational logical truths afforded by necessitation, it manages to jumble together (M) and (C). That’s a glittering miracle of logical concision, but a sorrowful monument of philosophical muddle (which fn 58 is in charge of further vandalising).
For example, \(\varphi _{1}\) will have the form of the conjunction of ‘A man with i hairs is bald’ with the naive theory of vagueness, \(\varphi _{2}\) will have the form of the conjunction of ‘A man with \(i+1\) hairs is bald’ with the naive theory and \(\varphi _{3}\) will have the form of ‘A man with \(i+2\) hairs is bald’. Since the naive theorist accepts that ‘A man with 1 hair is bald’ is known but does not accept that ‘A man with 100,000 hairs is bald’ is known, and since it is a precise matter what the naive theorist accepts, by classical reasoning it follows that there is going to be some such i (cf fn 23). Thanks to an anonymous referee for feedback on the material in this fn.
To wit, it is a vague matter because it exhibits both main phenomena of vagueness. Firstly, it exhibits Sorites susceptibility: it is prima facie obvious [that, for every i, if ‘A man with i hairs is bald’ is known, so is ‘A man with \(i+1\) hairs is bald’] and it is prima facie absurd [that, for some i, ‘A man with i hairs is bald’ is known but ‘A man with \(i+1\) hairs is bald’ is not]. Secondly, it exhibits borderline cases: for some i, it is borderline whether ‘A man with i hairs is bald’ is known. Throughout, I take exhibition of these two phenomena as my criterion for attribution of vagueness (see Greenough (2003) for an in-depth discussion of the phenomena of vagueness). (For example, by this criterion, not only is it vague for which i ‘A man with i hairs is bald’ is known, but it is also vague for which i ‘A man with i hairs is bald’ is definitely known (definitely definitely known, definitely definitely definitely known etc.), so that knowledge of baldness is not only (first-order) vague, but also higher-order vague.) Notice that I’m thus not inferring vagueness in knowledge of baldness from vagueness in baldness; I’m inferring it from the fact that knowledge of baldness exhibits the two main phenomena of vagueness. Indeed, vagueness in Fness is arguably neither necessary nor sufficient for vagueness in knowledge of Fness: it is not necessary because, for example, it can be precise whether a tree is at least 100 ft tall and yet vague whether one knows, judging from the distance by the naked eye, that a tree is at least 100 ft tall; it is not sufficient because, for example, it can be vague whether a tree is tall and yet precise whether one knows, judging from the distance with a monocular, that a tree is tall (because, say, the monocular is so built as to have a threshold of detection passed only by trees that are at least 100 ft tall). Thanks to two anonymous referees for comments that prompted these elaborations.
Notice that either the naive theorist of vagueness accepts that \(\varphi _{2}\) is known or she does not, and that, either way, she accepts that a sentence (either \(\varphi _{2}\) or \(\varphi _{1}\)) is known, accepts that, if it is known, a certain other sentence (either \(\varphi _{3}\) or \(\varphi _{2}\)) is known, but does not accept that the latter sentence is known. Therefore, it’s not just that the naive theorist accepts that \(\varphi _{1}\) is known but does not accept that \(\varphi _{3}\) is known because the former does not entail the latter at least on her view (the objection I’ve discussed in the main text); she accepts that \(\varphi _{2}\) (or \(\varphi _{1}\)) is known but does not accept that \(\varphi _{3}\) (or \(\varphi _{2}\)) is known although the former does entail the latter even on her view! However, just like the objection I’ve discussed in the main text relies on a logical principle that fails in the relevant cases according to the naive theory, the objection I’m discussing in this fn relies on a normative principle (one should [accept the conclusion of an argument known to be valid if one accepts its premises]) that arguably fails in many [cases to be discussed in this paper] (fn 56) and does fail in the relevant cases according to the naive theory (see Zardini (2015b) for a general discussion; the alert reader will notice that failure of this principle also creates a further problem for the objection I’ve discussed in the main text!).
On recently popular views on which all knowledge is evidence (e.g. Williamson 1997), that implies that Greg does after all have entailing evidence about history. For what it’s worth, I find such views extremely problematic (see e.g. Zardini (2017) for an objection) and I’ll henceforth set them aside, but those who are more sympathetic to them might still profitably read the discussion in this section by substituting ‘nonentailing evidence’ for the relevant occurrences of ‘evidence’.
I assume a notion of strength such that a proposition with 100,000 independent conjuncts counts as much stronger than any of its conjuncts. Also, I work with a fairly coarse-grained notion of [certain evidence’s being “of the appropriate kind” to afford knowledge of a certain proposition] such that, if certain evidence counts as of the appropriate kind to afford knowledge of a certain proposition, it also counts as of the appropriate kind to afford knowledge of each other proposition of the same strength: appropriateness of kind has to do with how probative the evidence is rather than with what it is about (for example, if a casual recollection of yesterday’s breakfast is of the appropriate kind to afford knowledge of \(\langle \)Yesterday, Greg had an egg tart for breakfast\(\rangle \), it is also of the appropriate kind to afford knowledge of \(\langle \)Yesterday, Greg had sardines for lunch\(\rangle \): such a recollection is probative enough so that, roughly, if it supported the latter proposition, it would support it enough to afford knowledge of it, although, given what the recollection is about, it actually does not support that proposition). It is such a notion that makes compelling the presupposition in the main text that [Greg’s body of evidence is of the appropriate kind to afford knowledge of \({\mathfrak {H}}\) only if, for every \(1\le i\le 100{,}000\), his piece of evidence for \(H_{i}\) is of the appropriate kind to afford knowledge of \({\mathfrak {H}}\)] even if the former consists of 100,000 such pieces of evidence, for the sheer pooling of pieces of evidence concerning independent propositions does not plausibly lead to a more probative body of evidence concerning the conjunction of those propositions—such pooling only improves on what the evidence is about (i.e. the conjunction of those propositions) rather than on how probative the evidence is. And it is also such a notion that will make compelling one of the main points in Sect. 2.4 to the effect that a difference of one single conjunct between two propositions is too small a difference in strength to make a difference as to whether one’s evidence is of the appropriate kind to afford knowledge of them. Thanks to Laura Delgado and an anonymous referee for prompting some of these clarifications.
That is indeed vague, but then in quite a few situations it is also vague whether a belief is reliable enough to count as knowledge.
This immediately suggests an alternative kind of possible-world semantics and logic for the knowledge operator where the usual “for every such-and-such world”-clause is replaced by a “for the vast majority of such-and-such worlds”-clause (a bit more accurately, by a “for the vast majority of such-and-such worlds including the current one”-clause if factivity is to be preserved).
I assume that plausible idealisations on logical space can be made so that it does make sense to talk of such numbers.
For the sake of illustration, I focus throughout on a reliability constraint of the safety variety (e.g. Sainsbury 1997), but everything I say applies mutatis mutandis to reliability constraints of several other varieties (for example, to a reliability constraint of the sensitivity variety, e.g. Nozick (1981), pp. 167–288).
I actually don’t like this particular intuition pump. By the same token, if Greg knew that, yesterday, he had an egg tart for breakfast he’d virtually know that his belief about what he had yesterday for breakfast is not mistaken, and the same kind of intuition kicks in to the effect that it seems pretty clear that he doesn’t know that. I don’t think this gives any support to the wacky idea that Greg does not know that, yesterday, he had an egg tart for breakfast; to me, it’s pretty clear that the problem lies instead in the fact that, generally, an ascription along the lines of ‘Subject s knows that her belief that P is not mistaken’ would seem to convey (at some linguistic level or other) more than the mere content that s knows that [she believes [that P] and P]. I thus regard this particular intuition pump as rather useless to establish that Greg does not know \({\mathfrak {H}}\) (although I acknowledge its power to move many people to accept that). As far as I’m concerned, a much more useful intuition pump in the vicinity is the one appealing to the consideration of whether Greg knows that [\(H_{1}\) while also \(H_{2}\) while also \(H_{3} \ldots \) while also \(H_{100{,}000}\)]: if Greg knew \({\mathfrak {H}}\) he’d know that too, but it seems pretty clear that he doesn’t know that. I therefore much prefer to take the fourth reason actually to consist in this second intuition pump.
It is natural, and usual, for one to grant the main thrust of this paragraph by offering the diagnosis that, although, for every \(1\le i\le 100{,}000\), Greg knows that \(H_{i}\), in enough cases \(\langle H_{i}\rangle \) is not certain for Greg, so that the resulting uncertainties together conspire to prevent Greg’s knowledge of \({\mathfrak {H}}\). Although an adequate discussion of certainty lies beyond the scope of this paper, I should mention that I’m inclined to disagree with such a diagnosis, for I’m inclined to think that an approach similar to the one I’m developing in this paper for knowledge also applies to certainty. In particular, I’m inclined to think that \({\mathfrak {H}}\) is not known by Greg (and a fortiori not certain for Greg) even in some extreme cases where, for every \(1\le i\le 100{,}000\), \(\langle H_{i}\rangle \) is certain for Greg. To support this claim, notice that analogues of the first and fourth reasons given in this paragraph would seem to apply just as well to those cases. Admittedly, analogues of the second and third reasons given in this paragraph do not do so, for the informal notion of certainty is usually modelled probabilistically and modally so as to require value 1 and truth in all similar situations respectively. However, it is arguable that such modelling is justified only insofar as it captures the equivalence—crucial in the informal (sane) notion of certainty—roughly to the effect that \(\langle P\rangle \) is certain for s iff, on the vast majority of occasions, s is justified in believing and acting in total disregard of the hypothesis that it is not the case that P (‘the vast majority of’ rather than ‘all’ because even a simple logical truth cannot just be taken for granted on an occasion where it is put under intense theoretical scrutiny or attached high practical stakes). And it is also arguable that, in some cases, even if, for every \(1\le i\le 100{,}000\), on the vast majority of occasions, Greg is justified in believing and acting in total disregard of the hypothesis that it is not the case that \(H_{i}\) (for example, on the vast majority of occasions, Greg is justified in believing and acting in total disregard of the hypothesis that he has not been hired by the university), it is not the case that, on the vast majority of occasions, he is justified in believing and acting in total disregard of the hypothesis that \({\mathfrak {H}}\) does not hold. The usual probabilistic and modal modelling of the informal notion of certainty, while good enough for many purposes, actually misrepresents it in that it leaves out a crucial element corresponding to the “on the vast majority of occasions”-quantification—exactly the element that introduces noncollective structure into certainty (just as very high probability and lack of false belief in the vast majority of similar situations introduce noncollective structure into knowledge). Certainty is dissipated through aggregation no less than knowledge is. (Ditto for the correlated notion of absence of risk, see Sect. 3.1.) I should also mention that I don’t think that an approach similar to the one I’m developing in this paper for knowledge applies to evidence: none of the analogues of the reasons given in this paragraph would seem to apply to the case of evidence, and, in Zardini (2017), p. 549, fn 22, I’ve given what are in effect positive reasons for thinking that \({\mathfrak {H}}\) is part of Greg’s evidence (and a fortiori known by Greg) in the extreme case where, for every \(1\le i\le 100{,}000\), \(\langle H_{i}\rangle \) is part of Greg’s evidence. (I also think that analogous considerations apply to data, cf Zardini (2017), pp. 553–554.) While knowledge and certainty are dissipated through aggregation, evidence is perpetuated through it. I should finally mention that, for a somewhat opposite reason, I also don’t think that an approach similar to the one I’m developing in this paper for knowledge applies to (my understanding of) justification (whether prima facie or all-things-considered): while all the reasons given in this paragraph but the third one (justification does not require reliability) straightforwardly apply to yield the conclusion that Greg is not even justified in believing \({\mathfrak {H}}\), justification is not plausibly closed under 2ary conjunction (fn 33) in the first place: I may be justified in believing that Benfica will win the next Portuguese Liga and justified in believing that Atlético will win the next Spanish Liga while not being justified in believing that Benfica will win the next Portuguese Liga and Atlético will win the next Spanish Liga. While knowledge and certainty are dissipated through aggregation and evidence is perpetuated through it, justification breaks down under conjunction.
I take it that this paragraph has so discredited belief in \({\mathfrak {H}}\) that we should regard it not only as unknowledgeable, but also as untenable (see also Zardini (2018), pp. 238–239; a virtual corollary of this—emerging with the help of Diogo Santos—is that Greg’s knowledge of \({\mathfrak {H}}\) cannot be rescued by contextualist manoeuvres to the effect that, in some contexts, standards are low enough for ‘Greg knows \({\mathfrak {H}}\)’ to count as true, for decent standards can never be so low as to allow such a strong, unlikely, unreliable, arrogant—and indeed rather silly—belief to count as knowledge). This raises a puzzle, because, for all that this paragraph has shown, it would still seem that Greg is entitled to have some sort of general belief about the truth of the contents of his evidentially best beliefs about history (as opposed to a particular belief about the truth of, say, \(\langle H_{1,965}\rangle \)), indeed a belief affording him a single position from which, for every \(1\le i\le 100{,}000\), he can conclusively stand by his belief that \(H_{i}\) (as opposed to the multiple positions afforded to him by his beliefs that \(H_{1}\), that \(H_{2}\), that \(H_{3}\)..., that \(H_{100{,}000}\), and as opposed to the position afforded to him by his belief that the vast majority of \(\langle H_{1}\rangle \), \(\langle H_{2}\rangle \), \(\langle H_{3}\rangle \)..., \(\langle H_{100{,}000}\rangle \) are true, from which, for every \(1\le i\le 100{,}000\), he can only nonconclusively stand by his belief that \(H_{i}\)). The puzzle is then that the natural candidate for such a belief is the belief that, for every \(1\le i\le 100{,}000\), \(\langle H_{i}\rangle \) is true, which is just as untenable as belief in \({\mathfrak {H}}\). What is needed is a single content that is both suitably weaker than \(\langle \)For every \(1\le i\le 100{,}000\), \(\langle H_{i}\rangle \) is true\(\rangle \) and still strong enough to afford Greg a single position from which, for every \(1\le i\le 100{,}000\), he can conclusively stand by his belief that \(H_{i}\) (and preferably such that Greg is not only entitled to it, but also knowledgeable about it). Zardini (2015a), pp. 496–498 makes a proposal. Analogous comments apply to the analogous dialectic concerning counterfactual implication developed in Sect. 2.2.
Very important: since I’m interested in defending (C) and its relatives (which are principles of pairwise collection), throughout I assume conjunction to be a fixed-arity 2ary operation rather than a variable-arity operation, so that, further assuming that collection most naturally goes step in step with conjunction, the most natural arguments against collection need to go via (C) and its relatives (I’ll touch in Sect. 2.3 on a different argument where collection does not go step in step with 2ary conjunction). Thanks to Ricardo Santos for help with this issue.
Obviously, the same point can be made by taking any other order on the subscripts. Throughout, I focus on the usual order only for illustrative purposes.
To wit, in one direction, given (1\(^{\mathrm {G}}\))–(100,000\(^{\mathrm {G}}\)) and Greg’s knowledge that (ADJ) is valid, (C) implies (\(\hbox {TOL}^{\mathrm {G}}\)); in the other direction, (\(\hbox {TOL}^{\mathrm {G}}\)) trivially entails that, for every \(1\le i<100{,}000\), if Greg knows that \(\langle H_{1}\) and \(H_{2}\) and \(H_{3}\) ... and \(H_{i}\rangle \) and \(\langle H_{i+1}\rangle \) entail \(\langle H_{1}\) and \(H_{2}\) and \(H_{3}\) ... and \(H_{i}\) and \(H_{i+1}\rangle \), then, if he knows that [\(H_{1}\) and \(H_{2}\) and \(H_{3}\) ... and \(H_{i}\)] and knows that \(H_{i+1}\), he knows that [\(H_{1}\) and \(H_{2}\) and \(H_{3}\) ... and \(H_{i}\) and \(H_{i+1}\)], and those are the only instances of (C) that are relevant in Greg’s situation (recall fn 34). Even if you (understandably) find the implication in the latter direction rather feeble, notice that the implication in the former direction together with the observation about which instances of (C) are relevant in Greg’s situation suffices for the point I’m making, for it suffices to show that the argument from aggregation only targets (C) insofar as it targets what is in effect a correct tolerance principle implied by (C). Similar elucidations apply to similar “tantamountness”-claims in what follows.
It’s important to realise that such a reply to the argument from aggregation does place nontrivial constraints on admissible assignments of probability to “typical” pieces of knowledge (i.e. those pieces of knowledge that, as initial inputs, can enter into a process of aggregation that preserves knowledge at least to a certain extent). For example, it seems extremely plausible that, at least, one can aggregate a single piece of knowledge about physics with a single one about chemistry with a single one about biology with a single one about psychology with a single one about sociology. Under an extremely plausible assumption about how high a probability is required for knowledge (i.e. at least \(\ge .5\)), that implies that we should regard typical pieces of knowledge as having probability of at least \(\sim .9\), instead of, say, probability possibly as low as .8 (while (C) already implies that we should not regard typical pieces of knowledge as having probability possibly as low as .7). That actually strikes me as an independently plausible consequence, to the extent that I’m inclined to regard it as further evidence in favour of the reply under consideration to the argument from aggregation. Henceforth, I’ll assume at some places (e.g. Sect. 2.4) a very specific \(\sim .99\)-kind of assignment, thereby ensuring that quite a few pieces of knowledge can be aggregated while preserving knowledge, although everything I say can be so rephrased as to fit more liberal and less liberal conceptions of how many pieces of knowledge can be aggregated while preserving knowledge. (Observe that, given the same constraints, the reply under consideration to the argument from aggregation also allows one to aggregate—naturally, to a lesser extent—pieces of knowledge that, instead of being independent, are to some degree negatively dependent on one another.) Thanks to Carrie Jenkins and Bernhard Salow for pressing me on this point.
Analogous more ecumenical points apply to the other argument against closure to be considered in this paper. Thanks to Bernhard Salow for observations on the material in this paragraph.
This paper basically opens up a new route from the Sorites paradox to the Preface paradox. A route in the opposite direction is travelled in Dorothy Edgington’s works (e.g. Edgington 1992), where it is argued that the abstract probabilistic structure familiar from the Preface paradox is also instantiated by the Sorites paradox (in the latter case, with probability measuring however not how strongly a proposition is believed, but how true it is). There are important points of convergence between Edgington’s view on the Sorites paradox and mine: we both think that, for every i, ‘A man with i hairs is bald’ and ‘A man with \(i+1\) hairs is bald’ have similar degrees of truth (although Edgington doesn’t quite get to say that the latter is true if the former is), that, for every i, the argument from ‘A man with i hairs is bald’ to ‘A man with \(i+1\) hairs is bald’ is therefore acceptable (although Edgington doesn’t quite get to say that it is valid) and that the problem arises instead from the repetition of such an argument (although Edgington doesn’t quite get to say that it only arises from repetition that is iteration—i.e. repetition that takes the conclusion of one argument of the relevant kind as a premise for a further argument of the same kind—rather than from any old repetition: for example, for a large enough i, she doesn’t get to say that the argument from ‘A man with \(n_{1}\) hairs is bald and a man measuring \(n_{2}\) centimetres is short and a man weighing \(n_{3}\) grams is slim \(\ldots \) and a man born \(n_{i}\) seconds ago is young’ to ‘A man with \(n_{1}+1\) hairs is bald and a man measuring \(n_{2}+1\) centimetres is short and a man weighing \(n_{3}+1\) grams is slim \(\ldots \) and a man born \(n_{i}+1\) seconds ago is young’—which would seem just as compelling as the argument from ‘A man with \(n_{1}\) hairs is bald’ to ‘A man with \(n_{1}+1\) hairs is bald’ and which involves a repetition of argument by tolerance but no iteration of such an argument—is acceptable, see Zardini (2019c)). As far as I know, Edgington does not offer a substantial discussion of the consequences of the Preface paradox on an epistemic property such as knowledge, as opposed to a psychological property such as belief; her discussion of the latter does suggest though that she might be sympathetic both to the claim that, for every \(1\le i\le 100{,}000\), Greg knows that \(H_{i}\) and to the claim that Greg does not know \({\mathfrak {H}}\), in which case, because of her commitment to classical logic, she would have to accept that (C) is false, but then, as per the discussion in this paragraph, she would add that it is not plainly false and indeed that every one of its instances is very close to full truth. Thanks to an anonymous referee for pointing out the relevance of Edgington’s works for the project of this paper.
This is not to suggest that points similar to the ones I’ll be making do not apply to noncounterfactual implication (for they do, see Zardini (2019e)), but, in the context of this paper, it is simpler and clearer to focus on the counterfactual variety.
Such a difference immediately suggests an alternative kind of possible-world semantics and logic for the counterfactual-implication operator where the usual “for every such-and-such world”-clause is replaced by a “for the vast majority of such-and-such worlds”-clause (a bit more accurately, by a “for the vast majority of such-and-such worlds including the current one”-clause if modus ponens is to be preserved, which, since ‘If \({\mathfrak {I}}\) held and, [for every \(1\le i\le 100{,}000\), if \({\mathfrak {I}}\) held, \(C_{i}\)], then \({\mathfrak {C}}\) would hold’ would not seem to fare better than ‘If \({\mathfrak {I}}\) held, \({\mathfrak {C}}\) would hold’, would lead to failure of single-premise conditional proof for counterfactual implication—unless one goes in for the kind of move advanced in the last paragraph of Sect. 2.3, for the logic on which conditional proof operates stands to implication as the logic under which knowledge is closed stands to knowledge). Thanks to Andrew Bacon for discussion on surrounding issues.
This is not to suggest that I’m happy with every natural relative of (ADJ). For, while I’m happy with (ADJ) being chained together as the first argument with another valid argument, I’m not happy with its being chained together as the second argument with another valid argument. That is, on my favoured tolerant logic, while the principle of “adjunction on the premises” (if \( \Gamma , \varphi \, \& \, \psi \vdash \chi \) holds, \(\Gamma , \varphi , \psi \vdash \chi \) holds) is valid, the principle of “adjunction on the conclusions” (if \(\Gamma _{1} \vdash \varphi \) and \(\Gamma _{2} \vdash \psi \) hold, \( \Gamma _{1},\Gamma _{2} \vdash \varphi \, \& \, \psi \) holds) is not (essentially, because, given the law of excluded middle and the law of noncontradiction both of which I also favour, it would wreak havoc with tolerance, see e.g. Zardini (2015a), pp. 520–525 for details and discussion). Therefore, even in the very strong tolerant logic I favour, the fact that \(\varphi \) holds and the fact that \(\psi \) holds are not always tantamount to the fact that \( \varphi \, \& \, \psi \) holds—at least in the sense that the effect that \(\varphi \) holds and the effect that \(\psi \) holds fall short of the effect that \( \varphi \, \& \,\psi \) holds. Thanks to an anonymous referee for comments that inspired this fn.
An anonymous referee points out that analogous strategies might still be deployed to try to establish that Greg knows \({\mathfrak {H}}\) even if it is granted that the argument from aggregation fails to do so because of its invalidity. To wit, one could try to argue that the claim that Greg knows \({\mathfrak {H}}\) can instead be seen as noninferentially justified being an accurate judgement about Greg’s situation, or as inferentially justified in a different way (for example, something like this: “If one has true beliefs that \(P_{1}\), that \(P_{2}\), that \(P_{3}\)..., that \(P_{i}\) that are based on the best nonentailing evidence we can have about history, and no funny business is going on, one knows that [\(P_{1}\) and \(P_{2}\) and \(P_{3}\ldots \) and \(P_{i}\)]; for every \(1\le i \le 100{,}000\), Greg’s true belief that \(H_{i}\) is based on the best nonentailing evidence we can have about history, and no funny business is going on. Therefore, Greg knows \({\mathfrak {H}}\)”). In reply, while I can see that one might inattentively and unreflectively be pulled to some such judgements, I think that attention to the distinction between, on the one hand, knowing that \(P_{1}\), that \(P_{2}\), that \(P_{3}\)..., that \(P_{i}\) and, on the other hand, knowing that [\(P_{1}\) and \(P_{2}\) and \(P_{3}\ldots \) and \(P_{i}\)], and reflection on how differently these behave on the three dimensions of comparison discussed in Sect. 2.1 (strength, probability, reliability), should make any initial pull these judgements might have had vanish. (In any event, it is not part of the aims of the present project to accommodate such judgements (and it cannot be, as the project has the much harder aim to accommodate the contradictory judgement that Greg does not know \({\mathfrak {H}}\)!).) Notice that no such attention or reflection diminishes the initial pull of the judgements appealed to in the main text, which would seem to stand or fall with a modest antiscepticism about history according to which we know more than a couple of things about history.
If anything, it’s the final nail in its coffin, for, if \(\langle P_{1}\rangle \), \(\langle P_{2}\rangle \), \(\langle P_{3}\rangle \)..., \(\langle P_{i}\rangle \) do not even entail \(\langle P_{1}\) and \(P_{2}\) and \(P_{3} \ldots \) and \(P_{i}\rangle \), there is no relevant reason to start with for thinking that, if one knows that \(P_{1}\), that \(P_{2}\), that \(P_{3}\)..., that \(P_{i}\), one knows that [\(P_{1}\) and \(P_{2}\) and \(P_{3} \ldots \) and \(P_{i}\)]!
Still, the fact that the logic under which knowledge of possibly precise propositions is supposed to be closed is the same as a logic of vagueness is suggestive of the fact that a finite subject’s vision of possibly precise facts is blurred in a way analogous to how, according to that logic, vague facts are in themselves blurred—that the structure of the logical limitations that vagueness imposes on things is the same as the structure of the epistemological limitations that finitude imposes on how one sees things. That raises the question of whether, once we deviate from classical logic re the logic under which knowledge is supposed to be closed, we still need to deviate from classical logic also re the logic of knowledge itself. That question must receive a positive answer as long as the former logic still includes (ADJ) (which it should), for otherwise \((\mathrm {C^{F}})\) would follow (which it shouldn’t). (As I’ve just argued in the main text, the converse question of whether, when we deviate from classical logic re the logic of knowledge itself, we then need to deviate from classical logic also re the logic under which knowledge is supposed to be closed must also receive a positive answer as soon as (CLOS) is to be vindicated. We can now observe that the alternative strategy for vindicating (CLOS) criticised in the last paragraph would incur further problems even granting a grand scepticism about history according to which we do not know more than a couple of things about history. For one thing, (CLOS) would seem no more plausible than the stronger (and more natural) principle that \(\langle \)One knows that \(\langle P_{1}\rangle \), \(\langle P_{2}\rangle \), \(\langle P_{3}\rangle \)..., \(\langle P_{i}\rangle \) entail \(\langle Q\rangle \rangle \), \(\langle \)One knows that \(P_{1}\rangle \), \(\langle \)One knows that \(P_{2}\rangle \), \(\langle \)One knows that \(P_{3}\rangle \)..., \(\langle \)One knows that \(P_{i}\rangle \) entail \(\langle \)One knows that \(Q\rangle \), which the strategy in question is however unable to vindicate (since it is committed to each premise and to the negation of the conclusion of the relevant instances of that principle). For another thing, while the strategy in question might at least have a point when considering aggregation-like phenomena where the relevant instance of \((\mathrm {ADJ^{F}})\) is materially valid (and so where knowledge can at least to some extent reasonably be supposed to be closed under it), by its very own lights it cannot be a general strategy for vindicating (CLOS) by deviating from classical logic re the logic of knowledge itself without deviating from classical logic also re the logic under which knowledge is supposed to be closed, as witnessed, among other things, by aggregation-like phenomena where the relevant instance of \((\mathrm {ADJ^{F}})\) is not even materially valid (and so where knowledge cannot to any extent reasonably be supposed to be closed under it and hence cannot to any extent reasonably be supposed to be closed under classical logic).) Notice that, while some sporadic approaches to the argument from aggregation have already appealed to adoption of a nonclassical (typically, paraconsistent) logic, they have done so only at the less fundamental level of the logic under which knowledge (or, more typically, something like rational acceptability) is supposed to be closed (e.g. Priest 2006, p. 105), whereas it is to the best of my knowledge a novelty of the approach developed in this paper to do so also at the more fundamental level of the logic of knowledge itself.
Once we’re ready to consider substructural candidates not only for the logic of propositions about knowledge (such as e.g. \(\langle \)Greg knows that \(H_{1}\rangle \)), but also for the logic of propositions that are the objects of knowledge (such as e.g. \(\langle H_{1}\rangle \)), interesting avenues of inquiry open up. For example, instead of understanding “good” inferences to be those that merely preserve knowledge from the premises to the conclusion (as I’ve officially done in Sect. 1.1), we may understand them to be those that allow for the acquisition of knowledge of the conclusion on the basis of knowledge of the premises. Under this revised understanding, the inference from a proposition to itself is no longer “good”, so that only a substructural nonreflexive logic can be one where every formally valid argument corresponds to a “good” inference (see Moruzzi and Zardini (2007), p. 181; Zardini (2018), p. 242 for some more details on this idea).
To fix ideas, I assume that these are indeed the differences in probability and reliability between \({\mathfrak {H}}'\) and \({\mathfrak {H}}''\) (fn 36). If you think that such differences are actually not fine-grained enough to support the following train of thought, Greg’s situation can be plausibly further described so that the differences in probability and reliability between \({\mathfrak {H}}'\) and \({\mathfrak {H}}''\) get arbitrarily small. Indeed, by unusually modifying Greg’s situation so that his relevant beliefs are denumerably many, and by mapping them bijectively on, say, the rational interval [0, 1], we can, for \(a < 1\) and b arbitrarily small, let \(\langle \)Every belief in [0, a] is true\(\rangle \) and \(\langle \)Every belief in \([0,a+b]\) is true\(\rangle \) play the role of \({\mathfrak {H}}'\) and \({\mathfrak {H}}''\) respectively, so that also the difference in strength between them gets arbitrarily small.
To corroborate the compellingness of (SUBST), let’s try it out on another example. Suppose that Al and Bill both believe that every zebra has stripes after each has gathered his own inductive evidence, and suppose further that Al knows that every zebra has stripes whereas Bill ignores it. Then, it is compelling to think that the big difference between knowledge and ignorance requires, taking for instance the dimension of comparison of probability, that the difference between the probability on Al’s evidence (\(\textsf {pr}^{\mathrm {A}}\)) of \(\langle \)Every zebra has stripes\(\rangle \) and its probability on Bill’s evidence (\(\textsf {pr}^{\mathrm {B}}\)) is \(>.01\).
To corroborate the compellingness of (STRETCH), let’s try it out on another example (along the same lines of that in fn 47). Suppose again that Al and Bill both believe that every zebra has stripes after each has gathered his own inductive evidence, but now suppose further that, while Al counts as knowing that every zebra has stripes, \(\textsf {pr}^{\mathrm {A}}(\langle \)Every zebra has stripes\(\rangle )-\textsf {pr}^{\mathrm {B}}(\langle \)Every zebra has stripes\(\rangle )=.01\). Then, it is compelling to think that the application of the concept of knowledge can be so stretched that Bill also counts as knowing that every zebra has stripes.
To fix ideas, I assume that this is indeed a big enough difference to support the difference between knowledge and ignorance (cf fn 36). If you think that it is not big enough, just take a bigger one. Analogous comments apply to the other differences that, for the same purpose, I assume below in the main text to be big enough to support the difference between knowledge and ignorance.
Thanks to two anonymous referees for comments that led to substantial revisions of the material in this section.
The argument from concatenation has recently been revamped by DeRose (1999), p. 23, fn 14, followed by Lasonen-Aarnio (2008), p. 171; Schechter (2013). Schechter (2013), p. 439, fn 31, who works with justification rather than knowledge (fn 31), points out the vagueness connection (crediting it to Stewart Cohen), but decides to disregard it for two reasons that leave me unpersuaded. The first reason rests on the claims that single-premise closure “is not motivated by some kind of tolerance in the concept of justification” and that, “rather, it is motivated by the thought that deduction is fully epistemically secure”, where for deduction to be “fully epistemically secure” is for it to be such that “there is no loss of justification when a thinker engages in a competent deductive inference” (Schechter 2013, p. 430). Now, I’m not certain of what Schechter exactly understands by ‘tolerance’—maybe something superloaded like e.g. the idea that our use of the word ‘justification’ has not settled certain cases (i.e. the borderline cases) as positive or as negative, so that the resulting semantic indecision leaves us some leeway in how to go on and apply the word to such cases?—but, on the understanding operative in this paper (Sect. 1.1), a concept is tolerant iff, quite simply, it validates a principle such as (3) because the relevant differences, while ad rem, are too small to make a difference to its application. On such understanding, going back to putting things in terms of knowledge rather than justification, insofar as (M) (as well as (C)) is supposed to articulate the thought that deduction is fully epistemically secure it is in effect very naturally motivated by some kind of tolerance in the concept of knowledge. For it is rather obvious that the relevant deductions can lead to conclusions that, on a few dimensions of comparison (for example, those discussed in Sects. 2.1, 2.4: strength, probability, reliability), are worse than the premises (I’ve substantiated this point for the multi-premise case in Sect. 2.1 and I’ll substantiate it for the single-premise case in this section); the claim, in spite of this point, that the corresponding inferences cannot result in loss of knowledge is then in effect very naturally understood as relying on the claim that such differences are too small to make a difference to knowledge, which is in turn tantamount to the claim that the concept of knowledge is tolerant with respect to the epistemic differences that can occur in propositions that are premises and conclusions of those inferences. With respect to such inferences, deduction is fully epistemically secure—knowledge is closed under logical consequence—exactly because, with respect to such inferences, logical consequence is guaranteed only to relate propositions whose epistemic differences are too small to make a difference to knowledge (see Sects. 2.4, 3.4 for more elaboration on this). (I’ve been assuming a weak interpretation of Schechter’s quoted gloss on “full epistemic security”, according to which it consists in there not being a loss of knowledge simpliciter when a thinker engages in a competent deductive inference. However, there is another, stronger way of interpreting that gloss, according to which “full epistemic security” would consist in there not being any epistemic loss whatsoever when a thinker engages in a competent deductive inference (which is probably along the lines of what Schechter actually has in mind, since, on the weak interpretation, his claim that single-premise closure is motivated by the thought that deduction is “fully epistemically secure” boils down to the claim that single-premise closure is motivated by the thought that deduction leads from known premises to known conclusions, which comes perilously close to having the form ‘The thought that P is motivated by the thought that P’ and so perilously close to being trivially false). On this alternative interpretation, if (M) were motivated by the thought that deduction is “fully epistemically secure”, it would indeed not be motivated by some kind of tolerance in the concept of knowledge. However, on this alternative interpretation, the thought that deduction is “fully epistemically secure” is very implausible in that it clashes with the above-mentioned facts concerning the increase in strength and the decrease in probability and reliability from the premises to the conclusion of a deduction. Therefore, so motivated, (M) would not be a very interesting principle in the first place. Deduction is not an epistemically frictionless plane; however, it is epistemically smooth enough for knowledge to roll from its premises to its conclusions.) Schechter’s remark would thus not seem to manage to identify a plausible motivation for (M) that, when all is said and done, does not involve reliance on some kind of tolerance in the concept of knowledge. The second reason rests on the claim that “the major contemporary solutions to the sorites paradox—supervaluationism, epistemicism, degree theories, and so on—all agree that the major premise in a classical sorites argument is false”, and I take it that such a dubious claim has already been dealt with in Sect. 2.2. Thanks to Bernhard Salow for discussion on some of these issues.
We’d be able to derive this from Cate’s knowing the uncontroversial fact that [she only knows \({\mathfrak {F}}\) if \(\Delta \) is valid] by appealing to closure of Cate’s knowledge under modus ponens (fn 58) and a suitable version of the KK-principle. But the point is extremely plausible independently of such heavy-duty assumptions, and not because of the broadly antidogmatist idea that knowledge that \(\Delta \) is valid is a precondition on knowledge of \({\mathfrak {F}}\), but because of the broadly dogmatist idea that, further assuming that Cate already has a good enough inductive basis for knowing that her inferences are typically correct, knowledge that \(\Delta \) is valid is a result of knowledge of \({\mathfrak {F}}\) (knowledge of \({\mathfrak {F}}\) plus introspective knowledge that she has inferred \({\mathfrak {F}}\) by \(\Delta \) yields knowledge that she has inferred a true conclusion by \(\Delta \); given the facts that \(F_{1}\) and that her inferences are typically correct (both of which she knows), the fact that she has inferred a true conclusion by \(\Delta \) is then by far best explained by the validity of \(\Delta \)).
Strictly speaking, it is really tantamount to that fact plus the fact that the relevant 99, 998 instances of transitivity are materially valid (which they are, since, for every \(1\le i\le 100{,}000\), \(\langle F_{i}\rangle \) only involves very standard logical and mathematical concepts, and so, for every \(1\le i< 100{,}000\), \(\langle \delta _{i}\) is valid\(\rangle \) is arguably precise, see Sect. 2.3). For the sake of simplicity, I’ll henceforth ignore this latter, additional fact, which in effect could only be used to strengthen the points I’ll be making on the basis of the former fact (or indeed to replace the former fact to make those very same points).
Standard logic might not be best fit to discriminate in strength between two different true validity claims; standard epistemic logic might not be best fit to discriminate in knowledge between two different true validity claims; standard probability theory might not be best fit to discriminate in probability between two different true validity claims etc. This insensitivity is justified by the usual heavy-duty idealisations, but those idealisations are distorting when it comes to analysing the situations of our finite subjects. Presumably, those formal disciplines can be so extended as to lift such idealisations, and, without entering into any details, I presuppose that this is indeed so when I make discriminations such as those just made in the main text.
Even without the last three assumptions of the second last paragraph—which, for certain subjects, might indeed constitute an overintellectualisation—I note that it should be hardly controversial that every subject who for the first time infers such an astonishing conclusion as \({\mathfrak {F}}\) through a nonchalant derivation of 100, 000 steps as in \(\Delta \) does not (yet) know that conclusion (she only knows it once she has done enough in terms of double-checking the steps, having someone else confirming them, considering their wider role in \(\Delta \) etc.). Let’s suppose that Kate is an unreflective such subject, and observe how this claim can be buttressed by reasons similar to those supporting the claim that Cate does not know that, for every \(1\le i< 100{,}000\), \(\delta _{i}\) is valid. Firstly, \(\Delta \) is an extremely convoluted deduction, and it seems that Kate’s rather casual inferences, while of the appropriate kind, for every \(1 \le i < 1{,}000{,}000\), given knowledge of \(\langle F_{i}\rangle \) as initial premise, to afford knowledge of the conclusion of a deduction as short as the one from \(\langle F_{i}\rangle \) to \(\langle F_{i+1}\rangle \), are not of the appropriate kind, given knowledge of \(\langle F_{1}\rangle \) as initial premise, to afford knowledge of the conclusion of a deduction as long as \(\Delta \). (Notice that, in comparison with the first reason for why Cate does not know that, for every \(1\le i< 100{,}000\), \(\delta _{i}\) is valid, we’re now focusing on length rather than strength and on inferences’ being of the appropriate kind to transmit knowledge from the premise to the conclusion of a deduction of a certain length rather than on evidence’s being of the appropriate kind to support knowledge of a proposition of a certain strength.) Secondly, since, for every \(1 \le i < 100{,}000\), the difference between the probability on Kate’s epistemic state (\(\textsf {pr}^{\mathrm {K}})\) of \(\langle F_{i}\rangle \) and \(\textsf {pr}^{\mathrm {K}}(\langle F_{i+1}\rangle )\) although very low is plausibly \(>0\), \(\textsf {pr}^{\mathrm {K}}({\mathfrak {F}})\) can get extremely close at least to .5 (and indeed to 0 if the relevant kind of probability is superadditive as happens for example in the Dempster-Shafer theory, see e.g. Dempster (1967)). Therefore, Kate’s belief in \({\mathfrak {F}}\) would not seem likely enough for Kate to know \({\mathfrak {F}}\). (Notice that, in comparison with the second reason for why Cate does not know that, for every \(1\le i< 100{,}000\), \(\delta _{i}\) is valid, we’re now focusing on probability on overall epistemic state rather than on merely evidence, since, given Kate’s unreflective character, the support lent, for every \(1< i\le 100{,}000\), to \(\langle F_{i}\rangle \) by her overall epistemic state—a state that crucially includes her competent inferences leading up to her belief that \(F_{i}\)—might not be helpfully described as consisting merely in the possession of some evidence. Notice also that, on both “standard” and “standard nonstandard” probability theories, a principle of probabilistic monotonicity holds to the effect that, if \(\langle P\rangle \) entails \(\langle Q\rangle \), the probability of \(\langle Q\rangle \) is at least as high as the probability of \(\langle P\rangle \), but such probabilistic monotonicity is just one more usual heavy-duty idealisation made by those theories that is distorting when it comes to analysing the situations of our finite subjects (cf fn 54). I offer the beginnings of a theory of nonmonotonic probability in Zardini (2019c), and elaborate on the point just made in fn 56.) Thirdly, even the fallibilist reliability constraint is not satisfied by Kate’s belief in \({\mathfrak {F}}\) as based on \(\Delta \): it is not the case that, in the vast majority of similar situations, if Kate forms a belief in a proposition \({\mathfrak {F}}^{*}\) similar to \({\mathfrak {F}}\) on the basis of a [deduction \(\Delta ^{*}\) with true initial premise] similar to \(\Delta \), that belief is true—quite the opposite, in the vast majority of similar situations, Kate forms a belief in a proposition \({\mathfrak {F}}^{*}\) similar to \({\mathfrak {F}}\) on the basis of a [deduction \(\Delta ^{*}\) with true initial premise] similar to \(\Delta \) and that belief is false. (Crucially, notice that, on the contrary, the fallibilist reliability constraint is indeed satisfied, for every \(1 < i \le 100{,}000\), by Kate’s belief that \(F_{i}\) as based on \(\delta _{i-1}\): it is indeed the case that, in the vast majority of similar situations, if Kate forms a belief in a proposition \(\langle F_{i}^{*}\rangle \) similar to \(\langle F_{i}\rangle \) on the basis of a [deduction \(\delta _{i-1}^{*}\) with true initial premise] similar to \(\delta _{i-1}\), that belief is true.) Therefore, Kate’s belief in \({\mathfrak {F}}\) would not seem reliable enough for Kate to know \({\mathfrak {F}}\). Fourthly, if Kate knew \({\mathfrak {F}}\) she’d virtually know that [\(F_{1}\) whence in turn \(F_{2}\) whence in turn \(F_{3}\) ... whence in turn \({\mathfrak {F}}\) holds], but it seems pretty clear that she doesn’t know that. I also note that it should be even less controversial that less reflective Kate only knows \({\mathfrak {F}}\) if more reflective (but equally undefeated) Cate does. Thanks to Julien Dutant for pushing me on this issue.
With the point about nonmonotonic probability having been made in fn 55, we can now appreciate the full extent to which tolerant logics vindicate the idea that, for finite subjects, the conclusion of an argument known to be valid can be “weightier” than its premises. Classical logic actually already vindicates that idea for classically valid multi-premise arguments, already in that the conclusion of such arguments might not follow classically from any of their premises (don’t say that, in such arguments, the conclusion is still not weightier than the premises “taken together”, for this can only mean that it is not weightier than the conjunction of the premises, which, far from being somewhere among the premises of the argument, is in fact just one more conclusion that follows classically from the premises). Tolerant logics vindicate the idea also for classically valid multi-step single-premise arguments, already in that the final conclusion of such arguments might not follow tolerantly from their initial premise; tolerant logics naturally supplemented with nonmonotonic probability vindicate the idea also for every step of such arguments even if tolerantly valid, in that, in every such step, the probability of the conclusion might be lower than the probability of the premise although the former tolerantly follows from the latter. Notice that the point that, for finite subjects, the conclusion of a single-premise argument known to be valid can be less likely than its premise spells disaster for usual normative doxastic constraints on logical consequence (see Field (2015), pp. 42–54 for a recent favourable discussion): while the usual normative doxastic constraint that one should [believe the conclusion of an argument known to be valid if one believes its premises] already fails because of the points emerging with Greg’s situation, the usual Bayesian-whiffing retreat consisting in holding that, at least, one should [not have more lack of confidence in the conclusion of an argument known to be valid than the sum of the lacks of confidence one has in its premises] (as well as the simpler usual non-Bayesian-whiffing retreat consisting in holding that, at least, one should [believe the conclusion of an argument known to be valid if one believes the conjunction of its premises], which I’ve criticised on other grounds in Zardini (2018), pp. 260–261, fn 6) fails because of the points emerging with Cate’s situation. Those points might still leave open the prospects for a looser constraint to the effect that one should [not have a lot more lack of confidence in the conclusion of an argument known to be valid than the sum of the lacks of confidence one has in its premises], but, in addition to being subject to its own counterexamples (such as the first one given in Zardini (2015b), p. 252), such a constraint would anyway fall short of being specific to deductive consequence (as it would apply just as well to undefeated nondeductive consequence).
Interestingly, focus on metalevel propositions affords a perspective from which even Greg’s case is problematic not just because of the strength of the object-level conclusion, but also because of the strength of the metalevel proposition \(\langle \langle H_{1}\rangle \), \(\langle H_{2}\rangle \), \(\langle H_{3}\rangle \)..., \(\langle H_{100{,}000}\rangle \) entail \({\mathfrak {H}}\rangle \) (assuming that Greg arrives at \({\mathfrak {H}}\) from \(\langle H_{1}\rangle \), \(\langle H_{2}\rangle \), \(\langle H_{3}\rangle \)..., \(\langle H_{100{,}000}\rangle \) by 99,999 steps of (ADJ), see fn 33), and so not just because of aggregation, but also because of concatenation. (Similarly, even without ascending to such a perspective, Greg’s case is problematic not just because of the strength of the object-level conclusion, but also because of the length of the object-level deduction.)
With this treatment of (C) and (M) in place, we have a good standpoint from which to investigate the status of other interesting closure principles. To take an illustrative example, closure of knowledge under modus ponens (if one knows that \(\langle P\rangle \) and \(\langle \)If P, \(Q\rangle \) entail \(\langle Q\rangle \), then, if one knows that P and [that, if P, Q], one knows that Q) can be analysed into two components: an instance of (C) concerning one’s knowledge of \(\langle P\rangle \) and of \(\langle \)If P, \(Q\rangle \) and an instance of (M) concerning one’s resulting knowledge of their conjunction. That requires an instance of transitivity applied to [an instance of (C) and an instance of (M)], which is in general as problematic as instances of transitivity applied to two instances of (C) or to two instances of (M) for analogous reasons. Therefore, contrary to (C) and (M), closure of knowledge under modus ponens does not unrestrictedly hold. Still, in many cases, the relevant subject can also be assumed to know the conjunction of the premises (thereby dispensing with the relevant instance of (C) in the first place) and, in a few other cases, for the relevant subject, single-premise modus ponens (\( \varphi \, \& \, (\varphi \rightarrow \psi )\vdash \psi \)) is evident (so that, for her, that conjunction is epistemically at least as strong as the consequent), in such a way that, from one’s knowing the conjunction, it can always (that is, even in the presence of formal failure of transitivity) be inferred that one knows the consequent (thereby validating the relevant instance of transitivity applied to the relevant instance of (C) and the relevant instance of (M)). Therefore, in both kinds of cases (among other ones), closure of knowledge under modus ponens does hold. (I should also mention that there are tolerant logics where two-step modus ponens (\(\varphi , \varphi \rightarrow \psi , \psi \rightarrow \chi \vdash \chi \)) is valid (Zardini 2015b, pp. 244–245, fn 36), which, given (C) and (M), would yield closure of knowledge under modus ponens.) Similar comments apply to many other interesting closure principles.
A particularly interesting—since otherwise fairly recalcitrant—case is due to Joshua Schechter (personal communication in 2008, cf Schechter (2013), pp. 448–450 for discussion of a broadly related issue; any infelicity in the presentation of the case as well as the specific conclusion I draw from it are my sole responsibility). Presumably, there are some true principles of belief transition to the effect that, for every P, for some function \(\textsf {jus}\) from propositions and epistemic states to propositions, if one in epistemic state E is justified in believing that P and FURTHER\((\langle P\rangle ,E)\), one is justified in believing \(\textsf {jus}(\langle P\rangle , E)\) (where the relation between \(\langle P\rangle \) and \(\textsf {jus}(\langle P\rangle ,E)\) might be much tighter than logical consequence and ‘FURTHER\((\langle P\rangle ,E)\)’ might place many more restrictions than those familiar from usual closure principles). And, presumably, some such principles will deliver instances that can be chained together to form very long concatenations (the thought being that, whatever justified belief one has, there is always a transition one can make to another justified belief), some of them so long as to begin with an arguable case of justification but end with an arguable case of lack of justification. If so, the ensuing concatenation-like phenomenon cannot be treated by rejecting the relevant closure principle, thereby making a tolerant approach virtually inescapable.
Even without the last four assumptions of the second last paragraph—which, for certain subjects, might indeed constitute an “overknowledgeablification”—I note that it should be hardly controversial that every subject who for the first time receives such a detailed content as \({\mathfrak {P}}\) through an insouciant gossip of 100, 000 steps as in \(\mathrm {K}\) does not (yet) know that content (she only knows it once she has done enough in terms of double-checking the steps, having someone else confirming them, considering their wider role in \(\mathrm {K}\) etc.). Let’s suppose that, for every \(1\le i\le 100{,}000\), \(\hbox {Mateson}_{{i}}\) is, mutatis mutandis, an uninformed such subject, and observe how this claim can be buttressed by reasons similar to those supporting the claim that \(\hbox {Matteson}_{100{,}000}\) does not know that, for every \(1\le i<100{,}000\), \(\kappa _{i}\) has been successful. Firstly, \(\mathrm {K}\) is an extremely convoluted communication, and it seems that the Matesons’ rather casual communications, while of the appropriate kind, for every \(1 \le i < 1{,}000{,}000\), given knowledge of \({\mathfrak {P}}\) by \(\hbox {Mateson}_{{i}}\) as initial source, to afford the recipient’s knowledge of the content of a communication as short as the one from \(\hbox {Mateson}_{{i}}\) to \(\hbox {Mateson}_{i+1}\), are not of the appropriate kind, given knowledge of \({\mathfrak {P}}\) by \(\hbox {Mateson}_{{1}}\) as initial source, to afford the recipient’s knowledge of the content of a communication as long as \(\mathrm {K}\). Secondly, since, for every \(1 \le i < 100{,}000\), the difference between the probability on \(\hbox {Mateson}_{{i}}\)’s epistemic state (\(\textsf {pr}^{\mathrm {M}_{i}})\)—a state that crucially includes the competent communications leading up to \(\hbox {Mateson}_{{i}}\)’s belief in \({\mathfrak {P}}\)—of \({\mathfrak {P}}\) and \(\textsf {pr}^{\mathrm {M}_{i+1}}({\mathfrak {P}})\) although very low is plausibly \(>0\), \(\textsf {pr}^{\mathrm {M}_{100{,}000}}({\mathfrak {P}})\) can get extremely close at least to .5. Therefore, \(\hbox {Mateson}_{100{,}000}\)’s belief in \({\mathfrak {P}}\) would not seem likely enough for \(\hbox {Mateson}_{100{,}000}\) to know \({\mathfrak {P}}\). Thirdly, even the fallibilist reliability constraint is not satisfied by \(\hbox {Mateson}_{100{,}000}\)’s belief in \({\mathfrak {P}}\) as based on \(\mathrm {K}\): it is not the case that, in the vast majority of similar situations, if \(\hbox {Mateson}_{100{,}000}\) forms a belief in a proposition \({\mathfrak {P}}^{*}\) similar to \({\mathfrak {P}}\) on the basis of a [communication \(\mathrm {K}^{*}\) with true initial content] similar to \(\mathrm {K}\), that belief is true—quite the opposite, in the vast majority of similar situations, \(\hbox {Mateson}_{100{,}000}\) forms a belief in a proposition \({\mathfrak {P}}^{*}\) similar to \({\mathfrak {P}}\) on the basis of a [communication \(\mathrm {K}^{*}\) with true initial content] similar to \(\mathrm {K}\) and that belief is false. (Crucially, notice that, on the contrary, the fallibilist reliability constraint is indeed satisfied, for every \(1 < i \le 100{,}000\), by \(\hbox {Mateson}_{{i}}\)’s belief in \({\mathfrak {P}}\) as based on \(\kappa _{i-1}\): it is indeed the case that, in the vast majority of similar situations, if \(\hbox {Mateson}_{{i}}\) forms a belief in a proposition \({\mathfrak {P}}^{*}\) similar to \({\mathfrak {P}}\) on the basis of a [communication \(\kappa _{i-1}^{*}\) with true initial content] similar to \(\kappa _{i-1}\), that belief is true.) Therefore, \(\hbox {Mateson}_{100{,}000}\)’s belief in \({\mathfrak {P}}\) would not seem reliable enough for \(\hbox {Mateson}_{100{,}000}\) to know \({\mathfrak {P}}\). I also note that it should be even less controversial that less informed \(\hbox {Mateson}_{100{,}000}\) only knows \({\mathfrak {P}}\) if more informed (but equally undefeated) \(\hbox {Matteson}_{100{,}000}\) does.
It goes without saying that the strategy developed in this paper can be applied also to other aggregation- or concatenation-like phenomena. Some epistemological examples are given by certain situations I’ve studied in other works (Zardini 2012a, pp. 399–400, fn 34; 2017, p. 544, fn 9; 2019f). Another epistemological example is given by the situation studied by Dorr et al. (2014), where, given a sequence of 100,000 fair coins \(c_{1}\), \(c_{2}\), \(c_{3}\)..., \(c_{100{,}000}\), for every \(1\le i \le 100{,}000\), \(c_{i}\) will be tossed iff, for every \(j<i\), \(c_{j}\) lands tails (I’m modifying some inessential details of their presentation to make them fit our general format). Given knowledge of the set-up, Dorr et al. make (what we may dub) the “gambling” assumption that one knows that it is not the case that, for every \(1\le i \le 100{,}000\), \(c_{i}\) will land tails, and claim that this is inconsistent with the extremely plausible principle that, if one knows that a coin is fair and does not know that it will not be tossed, one does not know that it will not land tails. Notice that, in spite of their fn 5 (p. 279, which anyway ignores the availability of the naive theory of vagueness), Dorr et al. (title and) typically conduct their discussion as though they’ve established that that principle is plainly false, thereby manifesting the tendency stigmatised in Sect. 2.2—knowledge against the odds is against the odds of the vagueness debate. Setting that aside, Dorr et al.’s discussion is misleading in that it makes it look as though the argument has something specific to do with not knowing that a coin will be tossed. That is not the case, as we can run a stripped-down version of the argument where it is part of the set-up that all the coins will be tossed: the gambling assumption would then be claimed to be inconsistent with (what we may dub) the “no-magical-connection” principle that, for every \(1\le i \le 100{,}000\), if one knows that it is not the case that [\(c_{i}\) will land tails and, for every \(1\le j<i\), \(c_{j}\) will land tails] and one does not know that \(c_{i}\) will not land tails, one knows that it is not the case that, for every \(1\le j<i\), \(c_{j}\) will land tails. (Similarly, Dorr et al.’s discussion is also misleading in that it makes it look as though the argument has something specific to do with the future. That is not the case, as we can run versions of the argument where it is part of the set-up that the tosses take place in the past.) The no-magical-connection principle too is extremely plausible, because it is hard to see how else one knows that the conjunction in question is not the case. One prominent alternative would be that one knows of some sort of negative connection between \(\langle c_{i}\) will land tails\(\rangle \) and \(\langle \)For every \(1\le j<i\), \(c_{j}\) will land tails\(\rangle \), on the basis of which one could then know that the conjunction is not the case without knowing of either conjunct that it is not the case. However, one of the main points of the set-up is precisely to eliminate every such connection: adequately understood, the coins’ fairness requires that, even if, for every \(1\le j<i\), \(c_{j}\) lands tails, it remains totally open that \(c_{i}\) will land tails and that, even if \(c_{i}\) lands tails, it remains totally open that, for every \(1\le j<i\), \(c_{j}\) will land tails (in terms of probability (as understood in fns 24, 55), adequately understood the coins’ fairness requires that the conditional probability of one conjunct on the other is the same as its unconditional probability). Having noted this, it should also be noted that, just as, in Cate’s situation, the extreme plausibility of (M) is threatened by the minute but positive increase in strength and decrease in probability and reliability from one step to the next one, so is, in Dorr et al.’s situation, from the point of view of the gambling assumption, the extreme plausibility of the no-magical-connection principle. But the threat is deflected by reflecting that, from the point of view of the gambling assumption, it is very plausible that one’s knowledge of unrealised sequences of tails is vague in the situation in question: clearly, one knows that it is not the case that \(c_{1}\), \(c_{2}\), \(c_{3}\)..., \(c_{100{,}000}\) will land tails and, clearly, one does not know that it is not the case that \(c_{1}\) will land tails, but what’s the shortest sequence of the form \(c_{1}\), \(c_{2}\), \(c_{3}\)..., \(c_{i}\) one knows to be an unrealised sequence of tails? As per our criterion for attribution of vagueness (fn 22), that is an eminently vague matter, and points analogous to those made about the other aggregation- or concatenation-like phenomena discussed in this paper apply, with the result that the gambling assumption is indeed consistent with the no-magical-connection principle. For gamblers, there still is fairness exactly because there is vagueness. Having said all that, the gambling assumption is actually not that plausible: one’s epistemic position with respect to each unrealised sequence of outcomes is the same (though one would admittedly be more surprised by some than by others). (Compare: are you in a better position to know that ticket 111,111 of a fair lottery will not win rather than that ticket 110,779 will not win?) That is conclusive against the gambling assumption if \((\mathrm {C^{F}})\) is in place, and it is near conclusive even if (as I’ve argued in Sect. 2.3) \((\mathrm {C^{F}})\) isn’t in place, for, if it is absurd to suppose that one is in a position knowledgeably to identify the sequence of outcomes that will be realised, it is near absurd to suppose that one is in a position knowledgeably to rule out every unrealised sequence of outcomes (whereas, from the point of view of the gambling assumption, it is not at all absurd to suppose that one is in a position knowledgeably to rule out any unrealised sequence of outcomes, in such a way that, if one comes to rule out some of them, one might no longer be in a position to rule out other ones, cf fn 32). Dorr et al. are sensitive to this issue and so consider another situation where brutely statistical considerations would not seem to play a role: a leaf on a deciduous tree. Given a division of the period from the beginning of autumn to the end of winter into a sequence of 100, 000 equal intervals of times \(t_{1}\), \(t_{2}\), \(t_{3}\)..., \(t_{100{,}000}\), the gambling assumption is now replaced by (what we may dub) the “inductive” assumption that one knows that it is not the case that, for every \(1\le i \le 100{,}000\), the leaf will not fall at \(t_{i}\), which can then be claimed to be inconsistent with (what we may dub) the “no-natural-connection” principle that, for every \(1\le i \le 100{,}000\), if one knows that it is not the case that [the leaf will not fall at \(t_{i}\) and, for every \(1\le j<i\), the leaf will not fall at \(t_{j}\)] and one does not know that the leaf will fall at \(t_{i}\), one knows that it is not the case that, for every \(1\le j<i\), the leaf will not fall at \(t_{j}\). The no-natural-connection principle is extremely implausible because it is easy to see how else one knows that the conjunction in question is not the case: one knows of the negative connection between \(\langle \)The leaf will not fall at \(t_{i}\rangle \) and \(\langle \)For every \(1\le j<i\), the leaf will not fall at \(t_{j}\rangle \) consisting in their jointly violating a regularity of nature to an extent unmatched by either of them individually, on the basis of which one could then know that the conjunction is not the case without knowing of either conjunct that it is not the case (notice that such a connection can persist even in the presence of the stipulation made by Dorr et al. to the effect that the objective probability of the former conjunct conditional on the latter conjunct is high, as indicated by the fact that the unconditional objective probability of the former conjunct can still be higher than its objective probability conditional on the latter conjunct). Having noted this, it should also be noted that, just as, from the point of view of the gambling assumption, the extreme plausibility of the no-magical-connection principle is threatened by the minute but positive increase in strength and decrease in probability and reliability from one step to the next one, conversely the extreme implausibility of the no-natural-connection principle is mitigated by the positive but minute increase in strength and decrease in probability and reliability from one step to the next one, and, indeed, considerations from vagueness analogous to those vindicating the no-magical-connection principle vindicate the no-natural-connection principle.
For such subjects, \(\langle \langle P_{1}\rangle \) entails \(\langle P_{2}\rangle \) and \(\langle P_{2}\rangle \) entails \(\langle P_{3}\rangle \rangle \) (i.e. \(\langle \langle P_{1}\rangle \) entails \(\langle P_{2}\rangle \) which entails \(\langle P_{3}\rangle \rangle \)) is epistemically at least as strong as \(\langle \langle P_{1}\rangle \) eeennntaaaiiilllsss \(\langle P_{3}\rangle \rangle \) (where ‘eeennntaaaiiilllsss’ expresses the familiar notion one—or at least I—would express e.g. by uttering it while moving one’s hand through a concatenation of arguments written on the board to make it clear to one’s students that the initial premise entails the final conclusion), which is epistemically equivalent with \(\langle \langle P_{1}\rangle \) entails \(\langle P_{3}\rangle \rangle \).
References
Chisholm, R. (1966). Freedom and action. In K. Lehrer (Ed.), Freedom and determinism (pp. 11–44). New York: Random House.
David, M., & Warfield, T. (2008). Knowledge-closure and skepticism. In Q. Smith (Ed.), Epistemology: New essays (pp. 137–187). Oxford: Oxford University Press.
Dempster, A. (1967). Upper and lower probabilities induced by a multivalued mapping. Annals of Mathematical Statistics, 38, 325–339.
DeRose, K. (1999). Introduction: Responding to skepticism. In K. DeRose & T. Warfield (Eds.), Skepticism: A contemporary reader (pp. 1–24). Oxford: Oxford University Press.
Dodd, D., & Zardini, E. (Eds.). (2019). The a priori: Its significance, grounds, and extent. Oxford: Oxford University Press. Forthcoming.
Dorr, C., Goodman, J., & Hawthorne, J. (2014). Knowing against the odds. Philosophical Studies, 170, 277–287.
Dretske, F. (1970). Epistemic operators. The Journal of Philosophy, 67, 1007–1023.
Edgington, D. (1992). Validity, uncertainty and vagueness. Analysis, 52, 193–204.
Field, H. (2015). What is logical validity? In C. Caret & O. Hjortland (Eds.), Foundations of logical consequence (pp. 33–69). Oxford: Oxford University Press.
Fitch, F. (1963). A logical analysis of some value concepts. The Journal of Symbolic Logic, 28, 135–142.
Greenough, P. (2003). Vagueness: A minimal theory. Mind, 112, 235–281.
Harman, G. (1986). Change in view. Cambridge MA: MIT Press.
Hawthorne, J. (2004). Knowledge and lotteries. Oxford: Oxford University Press.
Hume, D. (1739). A treatise of human nature. London: John Noon.
Lasonen-Aarnio, M. (2008). Single premise deduction and risk. Philosophical Studies, 141, 157–173.
Lehrer, K., & Paxson, T. (1969). Knowledge: Undefeated justified true belief. The Journal of Philosophy, 66, 225–237.
Locke, J. (1690). An essay concerning humane understanding. London: Thomas Basset.
Makinson, D. (1965). The paradox of the preface. Analysis, 25, 205–207.
Moruzzi, S., & Zardini, E. (2007). Conseguenza logica. In A. Coliva (Ed.), Filosofia analitica (pp. 157–194). Rome: Carocci.
Nozick, R. (1981). Philosophical explanations. Cambridge MA: Harvard University Press.
Oms, S., & Zardini, E. (2019a). An introduction to the sorites paradox. In S. Oms & E. Zardini (Eds.), The sorites paradox. Cambridge: Cambridge University Press. Forthcoming.
Oms, S., & Zardini, E. (Eds.). (2019b). The sorites paradox. Cambridge: Cambridge University Press. Forthcoming.
Priest, G. (2006). Doubt truth to be a liar. Oxford: Oxford University Press.
Sainsbury, M. (1997). Easy possibilities. Philosophy and Phenomenological Research, 57, 907–919.
Schechter, J. (2013). Rational self-doubt and the failure of closure. Philosophical Studies, 163, 429–452.
Segerberg, K. (1971). An essay in classical modal logic. Uppsala: Filosofiska Föreningen och Filosofiska Institutionen vid Uppsala Universitet.
Shope, R. (1983). The analysis of knowing: A decade of research. Princeton: Princeton University Press.
Sorensen, R. (2002). Formal problems in epistemology. In P. Moser (Ed.), The handbook of epistemology (pp. 539–568). Oxford: Oxford University Press.
Sweeney, P., & Zardini, E. (2011). Vagueness and practical interest. In P. Égré & N. Klinedinst (Eds.), Vagueness and language use (pp. 249–282). Basingstoke: Palgrave MacMillan.
Sylvan, R. (2000). Sociative logics and their applications. Aldershot: Ashgate.
Williamson, T. (1995). Does assertibility satisfy the S4 axiom? Crítica, 27, 3–22.
Williamson, T. (1996). Cognitive homelessness. The Journal of Philosophy, 93, 554–573.
Williamson, T. (1997). Knowledge as evidence. Mind, 106, 717–741.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Zardini, E. (2008a). A model of tolerance. Studia Logica, 90, 337–368.
Zardini, E. (2008b). Living on the slippery slope. The nature, sources and logic of vagueness. Ph.D. thesis, Department of Logic and Metaphysics, University of St Andrews.
Zardini, E. (2009). Towards first-order tolerant logics. In O. Prozorov (Ed.), Philosophy, mathematics, linguistics: Aspects of interaction (pp. 35–38). St Petersburg: Russian Academy of Sciences Press.
Zardini, E. (2012a). Luminosity and vagueness. Dialectica, 66, 375–410.
Zardini, E. (2012b). Truth preservation in context and in its place. In C. Dutilh Novaes & O. Hjortland (Eds.), Insolubles and consequences (pp. 249–271). London: College Publications.
Zardini, E. (2014). Evans tolerated. In K. Akiba & A. Abasnezhad (Eds.), Vague objects and vague identity (pp. 327–352). Dordrecht: Springer.
Zardini, E. (2015a). \(\forall \) and \(\omega \). In A. Torza (Ed.), Quantifiers, quantifiers, and quantifiers: Themes in logic, metaphysics, and language (pp. 489–526). Dordrecht: Springer.
Zardini, E. (2015b). Breaking the chains. Following-from and transitivity. In C. Caret & O. Hjortland (Eds.), Foundations of logical consequence (pp. 221–275). Oxford: Oxford University Press.
Zardini, E. (2015c). Truth, demonstration and knowledge: A classical solution to the paradox of knowability. Theoria: An International Journal for Theory, History and Foundations of Science, 30, 365–392.
Zardini, E. (2016). No state a priori known to be factive is mental. Philosophical Issues, 26, 462–492.
Zardini, E. (2017). \({K}\nsubseteq {E}\). Philosophy and Phenomenological Research, 94, 540–557.
Zardini, E. (2018). Generalised Tarski’s thesis hits substructure. In N. Kellen, N. Pedersen, & J. Wyatt (Eds.), Pluralisms in truth and logic (pp. 237–276). Basingstoke: Palgrave MacMillan.
Zardini, E. (2019a). Instability and contraction. Journal of Philosophical Logic, 48, 155–188.
Zardini, E. (2019b). First-order tolerant logics. The Review of Symbolic Logic. Forthcoming
Zardini, E. (2019c). Non-transitivism and the sorites paradox. In S. Oms & E. Zardini (Eds.), The sorites paradox. Cambridge: Cambridge University Press. Forthcoming.
Zardini, E. (2019d). Seconde naïveté. In O. Bueno & A. Abasnezhad (Eds.), On the sorites paradox. Dordrecht: Springer. Forthcoming.
Zardini, E. (2019e). The underdetermination of the meaning of logical words by rules of inference. In D. Dodd & E. Zardini (Eds.), The a priori: Its significance, grounds, and extent. Oxford: Oxford University Press. Forthcoming.
Zardini, E. (2019f). Open knowledge of one’s inexact knowledge. Typescript.
Zardini, E. (2019g). The bearers of logical consequence. Typescript.
Zardini, E. (2019h). Unstable knowledge. Typescript.
Funding
At different stages, this article was funded by an AHRC Postdoctoral Research Fellowship and by the FCT Research Fellowship IF/01202/2013 Tolerance and Instability: The Substructure of Cognitions, Transitions and Collections. Additionally, the article was prepared within the framework of the HSE University Basic Research Programme and funded by the Russian Academic Excellence Project 5–100. I also benefited from support from the Project FFI2008-06153 of the Spanish Ministry of Science and Innovation Vagueness and Physics, Metaphysics, and Metametaphysics, from the Project FFI2015-70707-P of the Spanish Ministry of Economy, Industry and Competitiveness Localism and Globalism in Logic and Semantics and from the FCT Project PTDC/FER-FIL/28442/2017 Companion to Analytic Philosophy 2.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Earlier versions of the material in this article were presented in 2009 at the Arché Audit (University of St Andrews), in the course Closure, Transmission, and Epistemic Circularity (co-taught with Dylan Dodd and Crispin Wright) at the Arché Summer School (University of St Andrews) and at the Formal/Traditional Epistemology Workshop The Lottery Paradox (University of Glasgow); in 2010, at an Epistemology Workshop (University of Copenhagen) and at the 3rd Vagueness and Physics, Metaphysics, and Metametaphysics Workshop (University of Barcelona); in 2015, at the Workshop Puzzles of Knowledge (University of Lisbon); in 2016, at the LanCog MELL Seminar (University of Lisbon) and at the 8th SEFA Conference (University of Oviedo); in 2017, at the 6th Entia et Nomina Workshop in Patnem (Ghent University/University of Gdańsk) and at the 2nd Formal Methods and Science in Philosophy Conference in Dubrovnik (Inter-University Centre); in 2018, at the LEME Seminar (Federal University of Rio de Janeiro). I’d like to thank all these audiences for very stimulating comments and discussions. Special thanks go to Andrew Bacon, Jens Bjerring, Laura Delgado, Pedro Dinis, Dylan Dodd, Julien Dutant, Philip Ebert, Miguel Ángel Fernández, Hartry Field, Mikkel Gerken, Patrick Greenough, Carrie Jenkins, Dan López de Sa, José Martínez, Nikolaj Pedersen, Graham Priest, Stephen Read, Sònia Roca, Sven Rosenkranz, Bernhard Salow, Diogo Santos, Ricardo Santos, Joshua Schechter, Martin Smith, Ernest Sosa, Célia Teixeira, Rafał Urbaniak, Crispin Wright and two anonymous referees.
Rights and permissions
About this article
Cite this article
Zardini, E. Closed without boundaries. Synthese 199 (Suppl 3), 641–679 (2021). https://doi.org/10.1007/s11229-019-02352-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02352-0