Investigating populations in generalized Darwinism

Abstract

Darwinian evolution is a population-level phenomenon. This paper deals with a structural population concept within the framework of generalized Darwinism (GD), resp. within a generalized theory of evolution. According to some skeptical authors, GD is in need of a valid population concept in order to become a practicable research program. Populations are crucial and basic elements of any evolutionary explanation—biological or cultural—and have to be defined as clearly as possible. I suggest the “causal interactionist population concept” (CIPC), by R. Millstein for this purpose, and I will try to embed the approach into a generalized evolutionary perspective by mathematically formalizing its key definitions. Using graph-theory, (meta-) populations as described in the CIPC can serve as proper clusters of evolutionary classification based on the rates of interactions between their elements. I will introduce the concept of a cohesion index (CI) as a measurement of possible population candidates within a distribution of elements. The strength of this approach lies in its applicability and interactions are relatively easy to observe. Furthermore, problems of clustering tokens (e.g. of cultural information) via typicality, e.g. their similarity in intrinsic key characteristics, can be avoided, because CIPC is a (mainly) external approach. However, some formal problems and conceptual ambiguities occur within a simple version of this CI, which will be addressed in this paper as well as some possible applications.

Introduction

For some years now, scientists and philosophers have been postulating a generalized theory of evolution, respectively a generalized Darwinism (GD) as a form of interdisciplinary paradigm, cf. Aldrich et al. (2008), Mesoudi (2011), Schurz (2011) and Creanza et al. (2017). Evolutionary concepts such as variation, selection, inheritance, or population dynamics should, according to proponents of GD, be seen as abstract and formal traits of evolutionary systems in general, which allow for quantitative modelling and measurement and are thus not limited to the realm of biology. Cavalli-Sforza and Feldman (1981) or Boyd and Richerson (1988) were pioneers in the field: they were the first to propose quantitative mathematical models and simulations of cultural evolutionary systems. GD has also been understood as a “metatheoretical structure” (Hodgson 2006). The field is prosperous and growing and there are many attempts to classify it. For a recent overview, cf. Youngblood and Lahti (2018).

However, since GD-based theories appeared in the social sciences or humanities, there has also been skepticism and critique, e.g. Bryant (2004). For a detailed summary of critiques and defenses, cf. Aldrich et al. (2008). According to the work of Mesoudi (2011), GD might even possess the ability to synthesize the social sciences, just like the modern synthesis did in case of the life sciences in the first half of the twentieth century. In order to make this very interesting suggestion possible and to provide a “synthesis” of a similar kind, cultural macroevolution must somehow be explained in terms of cultural microevolution. But at this time, it is not clear, which phenomena outside classical evolutionary biology would in fact count as macro- or as microevolutionary. There is a growing body of literature about practical applications in cultural evolution and the use of phylogenetic methods outside of biology, cf. Mace et al. (2005) and Tehrani and Collard (2013), but from a philosophy of science perspective, many “conceptual issues” (Lewens 2015) lie still ahead. One of these issues lies in the concept of “population”. As Reydon and Scholz (2015, p. 581) formulate: “One major problem for GD […] is that a key element is missing from its ontology, namely, populations of the sort that constitute the principal units of evolution in Darwinian evolutionary theory”.

Motivated by that statement, this paper will proceed as follows: First, I will highlight the demand that GD is in need of a structural population concept in order to become a serious research agenda. Such a concept is still missing and “Generalized Darwinism in need of a population concept” section will present one candidate from philosophy of biology, namely R. Millstein’s “causal interactionist population concept” (CIPC). “Why use the CIPC in the context of generalized Darwinism?” section will discuss its benefits for GD. In “Abstracting away: populations as clusters of edges in a graph” section, I will offer a mathematical interpretation of the CIPC, using graph theory. This step can be understood as an interpretative generalization of the concept under inquiry. To facilitate readability, I will exemplify every step of the investigation on a very simple graph. “Challenges of the formalism” section deals with some formal issues and possible challenges for the model, resulting in a more fine-grained solution that can also be applied to more complex clusters of (cultural) interactions. “Challenges of the formalism” section then moves from population structure to population dynamics, briefly describing a possible way to understand the evolution, i.e. the development under the conditions of variation, selection and reproduction of the graph under investigation. “Grounding the formalism: possible applications” section gives some hints in possible directions of applying the formalism “in the field” and “Conclusion and future outlook” section concludes.

Generalized Darwinism in need of a population concept

Why does GD need a population concept?

Darwinian evolution is a population-level phenomenon.¹ It seems intuitive, that this should be true for GD as well. But population concepts vary greatly and biologists often do not characterize theirs or choose one in particular. Different population concepts yield different answers about which evolutionary processes are occurring and it becomes hard to track selective changes without clearly identifying the entity within those changes occur (Millstein 2010, p. 62). Despite the centrality of the population concept there is far less work on this terms’ ontology in the philosophy of biology, especially when compared to the long debate concerning the species concept. In the case of GD, things are even worse. What about populations in GD? Are there population in cultural evolution? Generally, I agree with Distin (2011, p. 215), that if any cultural evolutionary framework is to be taken seriously, then it is important that it should share explanatory advantages with its biological counterpart. The concept should enable us to draw fairly clear lines around cultural clusters, i.e. macroevolutionary entities, in a way that is in keeping with current understandings of both—cultural clusters and biological populations—and meets the theoretical demands that I have put on it. Up until now, there are hardly any suggestions of what a GD-population should be. It is not even clear, of what entities it might consist: persons, memes, actual social behavior, artifacts, abstract information or all of them together? But things are not completely hopeless. In a recent investigation of the concept of “cultural fitness”—a term almost as central to the study of GD as “population—(Ramsey and De Block 2017) suggest quite convincingly to adopt an agent-based perspective on cultural evolution. Instead of grounding our concept of cultural fitness on memes as cultural units (variant-based approach), the authors propose cultural populations as consisting of agents (individuals, persons) socially interacting with each other (organism-centered approach). This does by far not undermine the crucial differences between biological and cultural evolution, making them relatively independent instantiations of a Darwinian process (Ramsey and De Block 2017, p. 310). But since the arguments in favor of an organism-centered, and against a variant-based perspective are quite convincing, we tend to follow them.²

But let us return to the main question: What is a population and why is the concept so crucial for GD? (Godfrey-Smith 2009, p. 110) notes:

[A] Darwinian population is a collection of entities in which there is variation in character, the inheritance of some of those characteristics, and differences in how much individuals reproduce. These populations can be found at many levels.

One of the “levels” that Godfrey-Smith talks about could be cultural evolution. Another quote, which underpins the centrality of populations in Darwinian evolution—is given by Hodgson (2006, p. 16), emphases added:

As long as there is a population of replicating entities with varying capacities to survive, then Darwinian evolution will occur. Social evolution deals with populations of entities, including customs and social institutions that compete for resources. Accordingly, we believe that social evolution is Darwinian. This is not a matter of analogy; it is a partial description and analysis of reality

And finally, mathematician and biologist Martin Nowak writes:

Always keep in mind that the population is the fundamental basis of any evolution. Individuals, genes, or ideas can change over time, but only populations evolve (Nowak 2006, p. 4).

However, some questions remain unsolved, e.g. the problem of type-hood, to which we will turn now. Authors such as Reydon and Scholz (2015) claim that GD is in deep need of a valid population concept. According to their critical study, a successful application of GD³ in any domain outside of biology consists at least of two ontological claims: First, the application of what Dennett called the evolutionary algorithm, a processual structure consisting of the modules variation, selection and reproduction (Dennett 1995, p. 64). If elements of the system obey these principles in their development, it should be regarded as a Darwinian system by definition. Second, and this will be the gist of this paper, a valid population concept, which, according to the authors, is still totally absent from all recent approaches and programs that put themselves under the standard of GD.

Why a valid population concept? Reydon’s and Scholz’ (2015, p. 573) argument about the problems of GD can be condensed as follows. Rather than paraphrasing it, I will highlight an important quote from the paper:

The first, epistemological problem is that in the case of populations of social and economic entities, it remains unclear how the characteristic traits that define social and economic types are to be specified. […] This epistemological problem is rooted in the second, ontological problem; the ontology of populations in GD as groups of entities of the same type (i.e. sets or classes) does not match the ontology of populations in evolutionary theory as systems of interacting and reproducing entities.

What exactly is a “cultural type” and how can it be matched to a “system of interacting and reproducing entities”? This is far from clear. How do we classify instantiations of cultural processes as belonging to the same type? Is it because they look similar, because they descend from each other or because they are driven towards similar attractors in their evolutionary dynamics?

Instead of dealing with this troublesome issue, this paper will offer an alternative: populations of sociocultural systems should not be clustered by their type, but via their degree of causal connectivity. This is precicely what I will argue for in the sections to come. It becomes clearer that Darwinian evolution is a population-level phenomenon and that it will be hard to classify types of social entities. A successful version of GD should consist of an evolutionary algorithm (involving variation, selection, and reproduction) and a valid population concept, which enables us to group cultural entities in such a way, that avoids the type-problem and is still diagnostically efficient.

Clarifying GD’s ontological hierarchy, Reydon and Scholz (2015, p. 567) further distinguish between: (1) complex population systems, (2) populations and (3) entities within a population. The authors open up a tripartite hierarchy of evolving levels (similar as in multi-level selection theories), which are commitments of GD. The entities (3) that reproduce themselves are bundled in populations (2), and several populations constitute a complex population system (1). Populations evolve in Darwinian evolution and several connected populations can be interpreted as one metapopulation,⁴ which is a population of interacting populations, and thus a complex population system (1).

It seems that we are in need of a valid population concept, which also allows for an application on a higher level, i.e. a complex population system. In order to formulate such a structural population concept for GD, investigating its possible biological counterparts is probably a good way to start. Then it has to be shown, which (biological) population concept fits into the framework of GD in the most proper way. In the next subsection, one particular population concept is described: the CIPC. After describing its key definitions, its benefits for GD will be highlighted in “Why use the CIPC in the context of generalized Darwinism?” section.

The causal interactionist population concept (CIPC)

According to Roberta Millstein’s CIPC (Millstein 2010, p. 67) emphasis added):

(a) Populations […] consist of at least two conspecific organisms that, over the course of a generation, are actually engaged in survival or reproductive interactions, or both.

(b) The boundaries of the population are the largest grouping for which the rates of interaction are much higher within the grouping than outside.

Though location, gene flow, migration, or genetic relatedness are not included in the CIPC, they all may be indirect indicators of populations. Populations can split and unite again in time, all dependent on interactions between their elements. Interactions are the key features on which the CIPC population is built upon, and the defining focus on interactions will enable us to avoid the problem of intrinsic reproductive barriers that we face between members of different (biological) species. In this context, only external reproductive barriers can hinder any (possibly reproductive) interaction between members of different populations.

Definition (a) is ambiguous to a certain extent because it does not become clear at first sight what the difference between “survival” and “reproductive” interactions is or should be. The reason for that is that in the biological realm, only conspecific members can be part of the same population. On the other hand, she claims her approach to be neutral concerning a species concept, which seems a bit vague, if we recall that she has the term “conspecific” in her very first definition (a). The point is not clear, but we are not going to focus on the matter, because in GD, it seems even more problematic to apply any form of species concept.⁵ In what follows, we will therefore omit the aspect of conspecificity when talking about the CIPC in GD.

The level of complex population systems is encapsulated in the term metapopulation, which fits the conceptual hierarchy suggested above (cf. “Why does GD need a population concept?” section). Millstein (2010, p. 71) writes:

(c) Metapopulations consist of at least two local populations […], linked by migration or dispersal, such that organisms occasionally change which population they are a part of; rates of interaction within local populations are much higher than the rates of interactions among local populations.

(d) If the rates of interaction within local groupings are not significantly higher than the rates of interaction among local groupings, it is a patchy population.

Figure 1 [graphics from Millstein (2015, p. 10)] shows three cases: In case (i) a population “a” (defined by the interactions between their elements) splits up into two new (sub)populations “b” and “c”. The long vertical arrow between b and c elements indicates a (possibly reproductive) interaction between two separated populations. In case (ii), two separated populations form one metapopulation as defined above. The rates of interactions are lower between populations than within them, which is—according to Millsteins thesis (b)—crucial for defining its boundaries. The same is true for metapopulations (cf. argument (c) in the quote). Case (iii) describes a case where the rates of interactions between two populations became so frequent that they [according to thesis (d)] can be defined as one “patchy” population.

Fig. 1

The general framework of the CIPC and three exemplar cases: i population splitting of a population “a” into two subpopulations “b” and “c”, ii two populations “a” and “b” forming a metapopulation and iii a patchy population “a”

In the next section we will argue that the CIPC is probably the best candidate to count as a proper population concept in GD.

Why use the CIPC in the context of generalized Darwinism?

Commonly accepted criteria for population membership

What is the current state of affairs in the (biological and philosophical) debate on population concepts—i.e., what is available in the literature for us to choose from? In other words: what is a population and what are possible conditions for population membership?

Millstein’s CIPC meets common requirements on population concepts from the literature, esp. “causal connectivity”. What are those requirements? From a theoretical perspective, there are many ways for individuals to be “delimited as a grouping such that the grouping can undergo population dynamics” (Stegenga 2016, p. 26). But population dynamics is not the same as population structure. (Stegenga 2016) recently collected 8 possible general conditions for membership in biological populations from the literature of the past 50 years. The following list, which can be understood as sorted by degressive relevance, includes (ibid.: p. 6):

• 1. Variable phenotypes (V)

• 2. Fitness differences (F)

• 3. Heritable fitness (H)

• 4. Causal connectivity (CC)

• 5. Genealogical individuality (G)

• 6. Conspecificity (S)

• 7. Geographic proximity (P)

• 8. Typology (T)

V, F and H can already be found in Lewontin (1970). CC is given in the CIPC, which we described in the last section (Millstein 2010), where causal interactions are mostly seen as reproductive interactions or at least fitness affecting causal interactions. Conditions G, S, P and T are judged as being quite too narrow, even in the context of biology. They are proved to be unnecessary constraints (Stegenga 2016, p. 7), because they face many counterexamples and are not general enough. Furthermore, we can think of any possible combination of conditions, e.g. in the case of Futuyma (1986), who combines G, S and P. As we will see in “Why use the CIPC in the context of generalized Darwinism?” section, Millstein’s CIPC combines CC and S. But both take for granted V, F and H, which indeed seem to be the conceptual core of any population concept and represent the “evolutionary algorithm”, that we already mentioned above (“Why does GD need a population concept?” section). Stegenga (2016) then goes on to discuss CC in more detail, because for him it seems to be a crucial feature of population membership, maybe as crucial as V, F and H.

Nevertheless, after dealing with CC he concludes by arguing for a strong “population pluralism”, based on the fact that “individuals in a biological population are related to each other by specific causal interactions which affect reproduction and survival, which are manifold in kind, and that manifest to varying degrees.” (Stegenga 2016, p. 16). This diversity of causal interactions (e.g. eating, caring, communicating, mating, parasitism, symbiosis…) is so vast, that it will be hard to determine, which causal interactions should count as conditions for membership and which should not even if we only focus on fitness affecting interactions.⁶ However, even if “causal connectivity” as one condition for population membership is not free of issues, Stegenga and most other authors agree that it is a crucial requirement.

Let me emphasize that my suggestion of a particular population concept for GD is by no means a denial of “population pluralism”, which Stegenga and others have argued for. To the contrary, in GD and cultural evolution they may be even more possibilities to group individuals, than in biological evolution. But to choose from a certain variety of available concepts—to be a pluralist—means that you need some concepts at least. I believe that we have at least two good reasons to choose the CIPC—i.e. a population concept based on causal cohesion—for this particular research domain, as the next subsection will show.

Near decomposability and avoiding the type-problem

We have seen that several candidates for a valid population concept are on the market in theoretical biology and the philosophy of biology and that the CIPC meets crucial and common requirements. Choosing Millstein’s concept over others has two reasons. The first is that Millstein’s CIPC is a clear instantiation of the principle of “Near decomposability”, which proved very useful in the study of evolution. Secondly, because it focusses on external relations (interactions) rather than internal features of the elements of the grouping. Both reasons make the CIPC very attractive for GD.

• 1. Near decomposability

According to Simon (2002), “Near decomposability” (ND) is a fundamental property that appears to be shared by all multicelled organisms. Such organisms consist of a hierarchy of components, such that, at any level of the hierarchy, the “rates of interaction within components at that level are much higher than the rates of interaction between different components” (ibid.: p. 587). Systems with this property are called ND systems, and it can be modular organisms, populations of organisms or—as I want to implement here—populations of sociocultural entities. Millstein (2009) as well as Reydon and Scholz (2015, p. 578) claim that Darwinian populations have the ontological status of individuals (not classes or sets). “Individuality” is a concept that itself needs clarification, but let me emphasize that it has explicitly been defined, e.g. by DiFrisco (2018), in terms of having an ND structure.⁷ So if populations (either in the biological or cultural sense) should be treated as individuals, their ND properties can be a clear indicator of that—and Millstein’s CIPC provides them.

Furthermore, it has been shown that under the usual conditions of mutation and natural selection, ND systems will increase in fitness, and therefore reproduce at a much faster rate than systems that do not possess the property. This result has been proven mathematically on several occasions, cf. e.g. Simon (2002, p. 588). It seems rational to prefer a population concept, that makes use of ND (like CIPC), since it could explain why some populations increase in fitness, while others do not, and thereby provide an evolutionary explanation. Furthermore, and this is even more important, ND systems are not limited to the realm of biology. The concept was explicitly created to be applicable in cultural evolution as well, which makes it very attractive for GD. One of the several fields, where (modular) ND systems are already investigated, is e.g. the framework of economic interactions, cf. Marengo et al. (2005).

• 2. Focusing on external relations: avoiding the type-problem

Another advantage is the high degree of ontological applicability for GD. The CIPC does not define “populations” via intrinsic properties of members of a grouping, which are similar in key characteristics, share typical features etc. Instead, the CIPC gives a purely external definition of what a population is (external at least from a member’s perspective): not the traits of the members determine who belongs to the population and who does not; all that matters are the interactions between the members, resp. their density. This approach must also seem very attractive for proponents of GD, since it avoids (possibly problematic) discussions about (possibly typical) traits or features such as cultural genes (“memes”), or of (possibly mental) content, which members of the particular Darwinian population might (or might not) share. In this sense, Millstein’s approach is minimalistic—it leaves internal traits out—but it is rich in ontological transferability.

In the next section, I will try to give a more formal interpretation of the CIPC. This approach can be understood as an interpretative generalization of the (biological) population concept.

Abstracting away: populations as clusters of edges in a graph

Why formalize the CIPC?

Until now, the CIPC has not been mathematized. When addressing the issue whether, and under which circumstances, a particular distribution of biological individuals should be treated as a metapopulation or a patchy population (cf. Fig. 1), Millstein seems to be rather skeptical of a mathematical approach. She writes Millstein (2010, p. 80), (emphasis added):

A numerical value could be put on the relative strengths of those interactions (future work might consider how best to do this) to specify where to draw the line, but it is hard to see how any particular value could be defended. Any chosen numerical value would be fairly arbitrary […].

As in almost all biological or evolutionary terms, definitions have limits and exceptions, and concepts fall victim to a certain amount of ambiguity. Still, formalization can prove very useful, because it can bring about results or issues which are surprising or even counterintuitive to a certain extent. One such example in our particular case is the emergence of a populations’ “core” and a “periphery” (cf. “Formal problems: Which is the “right” population candidate?” section). A possible formal approach can also be used as a methodological tool for future investigations. If we want to interpret a given distribution of cultural agents (e.g. persons communicating with each other), which we observed, a formal version of CIPC can help us determine which clusters can count as cultural populations and how to cluster the network. Last but not least, formally abstracting from a target domain (biological systems) and re-specifying content to another base domain (cultural systems) provides a better explanatory solution for GD than just mere analogizing. This is only natural, since GD aims to show general (abstract) principles of evolutionary systems (such as a formal definition of “variation”, “reproduction” or a valid population concept); which explicitly denies the procedure of searching for biological analogies via similarity of phenomena. Although analogizing on the one hand and finding abstract principles and respecifiying them in another target domain on the other hand may resemble each other, they are not the same. In the past, this has often been confused, cf. Dollimore (2014, p. 376).

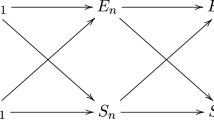
Figure 2 visualizes the difference between a one-step similarity based analogy (I) and a two-step based generalization using an abductive inference from a base to a formal principle and a respecification of this principle to a target domain (II). For a much more detailed analysis in the context of GD and cultural evolution, cf. Baraghith and Feldbacher-Escamilla (2020).

Fig. 2

Difference between a one-step similarity based analogy (I) and a more fruitful two-step based generalization (II)

How to formalize the CIPC: the “cohesion index”

How can the conceptual structure of the CIPC be formalized? I suggest simple graph theory, cf. Tittmann (2011), for our purpose. Graph theory provides us with the opportunity to investigate only the topological features of a network structure, which I want to embed in our definition of a GD population.⁸

Any graph $G$ is determined by the set of its nodes/elements $E$ and the edges/connections $I$ between nodes. We write: $G = \left( {E,I} \right)$. Let us take Millstein’s definition (a) of a population seriously and assume a population to be a set of elements E = {e₁, e₂, …, e_n}. The agents of the population are represented by the nodes of the graph, whereas the interactions (I) between them are represented by the edges.

As shown in Fig. 3, we assume a finite graph $G = \left( {E,I} \right)$, consisting of a set of elements E = {1, 2, …, 9} and a total number of #I = 10 interactions between them. That means:

Fig. 3

A possible CIPC graph G. Nodes represent members of the population(s), edges show their interactions

$$G = (\{ 1,2, \ldots ,9\} ,\{ a,b,c,d,e,f,g,h,i,j\})$$

The interactions I in G are defined by the nodes they connect:

$${\text{a}} = \left\{ {1,2} \right\},{\text{b}} = \left\{ {1,4} \right\},{\text{c}} = \left\{ {2,3} \right\},{\text{d}} = \left\{ {3,4} \right\}, \ldots ,{\text{ j}} = \left\{ {6,7} \right\}.$$

For now, let all the interactions be weighted equally and let us just observe their numbers. How can we cluster the elements into a plausible (macrolevel) structure? According to Millstein’s CIPC definition (b), the “boundaries of a population are those groupings where the rates of interactions are much higher within than without”.⁹

That means that we have to assume a partition between internal (I_i) and external interactions (I_e) and then simply observe the given distribution. The easiest way is just to count the internal edges and put them in relation to the external ones. Depending on that, we cluster elements of G (which is the general domain) into possible population candidates (A, B, C…, N) and see if they fit definition (b). Mathematically speaking, such candidates are possible subgraphs of G.

$A \subset G$ holds for A and analogously for other population candidates (B, C,…, N).

The two different types of interactions, I_i and I_e, are (set-theoretically) defined as follows:

$$I_{i} \left( A \right) = \left\{ {\left( {e_{n} ,e_{m} } \right): \left( {e_{n} ,e_{m} } \right) \in I, e_{n} \in A, e_{m} \in A} \right\}$$

$$I_{e} \left( A \right) = \left\{ {\left( {e_{n} ,e_{m} } \right): \left( {e_{n} ,e_{m} } \right) \in I, e_{n} \in A, e_{m} \notin A} \right\},$$

where $e_{n}$ and $e_{m}$ denote elements (nodes) of A, which is a subgraph of G.

We can now define possible clusters of elements that can—given by the number of internal compared with the number of external interactions—constitute a particular population candidate (PC) in G. In order to achieve this, I shall introduce a cohesion index (CI),¹⁰ where t denotes an axiomatic threshold that has to be exceeded based on definition (b) of CIPC:

$$CI_{PC} = \frac{{\# I_{i} \left( {PC} \right)}}{{\# I_{e} \left( {PC} \right)}} \ge t > 1$$

Which PCs fit Millstein’s definition (b)? Table 1 lists some possible options (by far not all possible subgraphs of G!) and outcomes of this algorithmic procedure. Capital letters (A, B,…, J) indicate subgraphs of G, of which I calculated the CI.

Table 1 Population candidates (A–E) as subgraphs of G. Candidates D–J count as real populations, given the cohesion index (CI)

One element alone (as in subgraph A) cannot constitute a population, which is trivial given Millstein’s definition of a population. The set of elements 1 and 2 (candidate B) have more external than internal interactions and therefore cannot count as a population, as well. In C the interactions are balanced but still not enough for I_i to be higher than I_e. The cluster D for example clearly fits the definition because $\# I_{i} > \# I_{e}$ holds for it. It is a “Millsteinian population”, depending on t.

For D, we have:

$$CI_{D} = \frac{{\# I_{i} \left( D \right)}}{{\# I_{e} \left( D \right)}} = \frac{4}{1} \ge t > 1$$

The case is almost analogous for E, except that the graph is not exactly symmetric on both sides, but we nevertheless have $\# I_{i} \left( E \right) = 4$. For illustrative purposes, the CI’s numerical values of the particular candidates are also depicted in Fig. 4. Any proper union (according to the CI’s definition) of two sets of edges $D \cup E$ constitutes a metapopulation in the sense of Millstein’s definition (c) of the CICP. Still, the question is how to constitute such a proper union.

Fig. 4

The particular CI’s numerical value of each population candidate in G

Additionally, one could consider weighting the interactions differently. In the process of cultural evolution, some social interactions are more important than others, depending on who the person is that you interact with, or what the content of the interaction is about. Frequency of certain interactions also plays a role. E.g.: Content bias (based on intrinsic attractiveness), model bias (prestige, age, similarity) or frequency dependent bias (conformity or anti-conformity) are all forces that strongly influence change in cultural variation of the population dynamics—given by interactions—over time. For an overview, cf. Mesoudi (2011, p. 57). Therefore, it seems rational to assume that not all interactions are weighted equally, as we have done up to this point. For each interaction I (be it internal or external), we can assume a weight function w_i ≥ 0.

$$CI_{PC} = \frac{{\# I_{i} \left( {PC} \right) \times w_{n} }}{{\# I_{e} \left( {PC} \right) \times w_{m} }} \ge t > 1$$

Some interactions can have more weight than other interactions, depending on any extra information that we have of the individual situation/context. Particular edges (or nodes) could count double or even triple, whatever their internal nature is like. There could also be different “kinds” of interactions, similar as Millstein’s “survival” or “reproductive” interactions, c.f. her definition (a), which can influence the CI in positive or negative ways.

However, since I just wanted to observe the topological features of the graph-based CIPC and avoid any notion or justification about “internal features” of the interactions within this investigation, I will not deepen the matter in this paper, although some words about it will be lost in “Grounding the formalism: possible applications” section. In the next chapter, I will concentrate on conceptual ambiguities and formal problems that occur within the CIPC and possible solutions to the latter.

Challenges for the formalism

Which is the “right” population candidate?

Despite the approach’s attractiveness and simplicity, there is at least one formal problem that occurs with this simple version of a cohesion index for cultural (or biological) populations. Although it may provide us with a mathematical tool to describe and find population candidates within a finite distribution (graph) of elements (nodes) and interactions (edges) by identifying subgraphs where the rate of internal interactions is much higher than the rate of external interactions, it is not clear which of these possible subgraphs are to prefer over others. This is true despite the fact that we may have some intuitions about the matter. Recall case (ii) of Fig. 1 of this paper. At first sight it becomes intuitively clear how to draw the boundaries between population a and b. However, in some cases (such as the one I want to present), things are not that unambiguous. Let me first clarify this point:

Given our particular graph G, we have several possibilities of defining population candidates (cf. Fig. 5), which all fit the definition of our cohesion index CI:

Fig. 5

Four possible population candidates within G

• 1.
  $$D = \left( {\left\{ {1, 2, 3, 4} \right\}, \left\{ {a,b,c,d} \right\}} \right) \quad CI_{D} = \frac{{\# I_{i} \left( D \right)}}{{\# I_{e} \left( D \right)}} = \frac{4}{1} \ge t > 1$$
• 2.
  $$E = \left( {\left\{ {6, 7, 8, 9} \right\}, \left\{ {g, h, i,j} \right\}} \right)\quad CI_{E} = \frac{{\# I_{i} \left( E \right)}}{{\# I_{e} \left( E \right)}} = \frac{4}{1} \ge t > 1$$
• 3.
  $$F = \left( {\left\{ {1, 2, 3, 4, 5} \right\}, \left\{ {a,b,c,d,e} \right\}} \right)\quad CI_{F} = \frac{{\# I_{i} \left( F \right)}}{{\# I_{e} \left( F \right)}} = \frac{5}{1} \ge t > 1$$
• 4.
  $$H = \left( {\left\{ {5, 6, 7, 8, 9} \right\}, \left\{ {f,g,h,i,j} \right\}} \right) CI_{H} = \frac{{\# I_{i} \left( H \right)}}{{\# I_{e} \left( H \right)}} = \frac{5}{1} \ge t > 1$$

• 5. …

Which subgraph is to prefer? Our intuition might tell us that we have to pick either candidate D or E, because their elements seem to be more “closely” connected. Given our approach, however, within this set of candidates it is probably F or H, because its CI reaches the highest numerical value, namely 5. Does this mean that we should always prefer the subgraph with the highest CI?

Recall Millstein’s second definition (b): “The boundaries of the population are the largest groupings for which the rates of interaction are much higher within the grouping than outside.” I think we can interpret this “much higher” in terms of a numerical value given by our cohesion index. That would simply mean, the higher the CI, the better the population candidate. Unfortunately, things turn out not to be that simple.

Take candidate (K), for example (Fig. 6). All but one edges are included in this subgraph, which gives us the following CI:

Fig. 6

A population candidate K with the highest possible CI in G; yet a counterintuitive result

$$K = \left( {\left\{ {1, 2, 3, 4, 5, 6, 7, 9} \right\}, \left\{ {a,b,c,d,e,f,h,i,j} \right\}} \right)\quad CI_{I} = \frac{{\# I_{i} \left( J \right)}}{{\# I_{e} \left( J \right)}} = \frac{9}{1} \ge t > 1$$

For our graph G, no higher CI can possibly be reached, except when we include all ten edges, which simply gave us: $\# I_{e} = 0$ and $\# I_{i} = 10$. That option however, is invalid.¹¹ This leads us to the very counterintuitive result that candidate K should be taken as the best possible population within our framework. Yet that is certainly not the best way to cluster the elements. In a simple graph like G, candidates D or E (cf. Fig. 5) seem to be the most proper ones, at least at first sight. This problem is also depicted in Fig. 4.

However, it is also not clear which nodes exactly we have to embed. What about element 5, for example? Should it belong to the left (D) or the right population (E), as candidate (F) suggests, or even be a member of both?¹² Obviously, this is an unsatisfactory state of affairs. It seems that a high CI alone is a necessary but not a sufficient condition of how to find the best population candidate in any given distribution of elements. What other formal tool can one establish here? I have two suggestions for improvement.

• 1. Neighborhood and density: core and periphery of a population

At this point, it is possible to introduce a measurement of the density of the interactions. The idea is not only to count the numbers of external and internal edges of subgraphs in G, but to take a closer look at how exactly the nodes are connected. Some nodes may be connected to many other nodes (resp. some members are interacting with many other members), some may be relatively independent. In our graph G, the latter is true for element 8, which has only one connection to another node. By contrast, element 6 “interacts” with 4 other elements.

In graph theory, two nodes $e_{n} ,e_{m} \in PC\left( G \right)$—where PC is the set of all nodes of the particular population candidate in G—which are connected by an edge $i = \left\{ {e_{n} ,e_{m} } \right\}$ are called “adjacent” (neighbouring) within G. The set of all adjacent nodes of any node $e_{n}$ is the “neighborhood” of $e_{n}$ (Tittmann 2011, p. 13).

The “degree” $\deg e_{n}$ of any node $e_{n} \in PC\left( G \right)$ is the number (#) of all edges connected with $x$.¹³ For example, in Fig. 7, element 1 has $\deg 2$, while element 6 has $\deg 4$. It becomes clear, that the more elements with a high degree are collected in a subgraph of G, the higher the density of the interactions within this very candidate. That means I can assume core and peripheral elements in our population, given by $\deg x_{n}$ of a node $x_{n}$, which has to be as high as possible. In our simple graph G, element 4 ($\deg 3$) has the second highest and element 6 ($\deg 4$) the highest reachable degree. Thus, element 6 is clearly a core element. The particular neighborhood of those core elements—all adjacent elements—thereby constitutes a core of a proper population candidate. The emergence of “core” and “periphery” in this context are examples of a more or less “surprising” result, which appeared because of the way we formalized the CIPC and were not intuitively given before this investigation. It shows how useful a formalization can be (cf. “Why formalize the CIPC?” section).

Fig. 7

Two population candidates given by the relatively high degree of their particular core element (node 4 and 6)

A persisting problem however is the ambiguity of element 5. Given the whole of G, it is not clear to which of both candidates it should belong (since it cannot be a member of both at the same time). At this point, I do not have a definite answer and shall treat element 5 as a borderline case, resp. a connecting element. The next subsection however, will suggest a possible way to go.

• 2. Cohesion and disjunctive edges

How robust is a cohesion of a graph regarding the removal of single edges? A “cut” is a partition of the nodes of a graph into two disjoint subsets. If such a cut is given by a single edge $i_{i} = \left( {e_{n} ,e_{m} } \right)$, this edge is called a “bridge”. In G, edges e and f are bridges. A bridge is a kind of “minimal cut”.

Cuts are important for us because they can show how “vulnerable” the cohesion can be. If element 4 and 5 (or 5 and 6) in G stopped interacting with each other, resp. their interaction became negatively selected for one reason or another, we could speak of two distinct populations. Obviously, this is not true for e.g. element 6 and 7. It takes more to decompose a core.

Final proposal for a clustering algorithm

The last two subsections provided us with some formal tools for a tentative last proposal concerning a mathematical reformulation of Millstein’s CIPC. This final suggestion tries to avoid problems mentioned in “Formal problems: Which is the “right” population candidate?” section of this paper (regarding the ambivalence of the “right” population candidate).

I suggest the following clustering algorithm to determine reasonable population candidates in a given distribution of interacting elements:

• 1. Find the core element(s) of the distribution, i.e. node(s) with $deg_{max}$.

• 2. Involve all nodes adjacent to the core element(s). This neighborhood constitutes the “core” of the population. Do not involve edges, which constitute a minimal cut (except the cut would only leave one element on whatever side, since a population needs at least two elements by definition). If an edge which constitutes a cut is reached, a new population begins.

• 3. Find the element(s) with next highest $deg$ in the neighborhood of the core elements. Together with their neighborhood, they constitute the particular population’s “periphery”.

• 4. Continue until you reach a minimal cut in each neighborhood.

In step 3, it is extremely important to import elements only in the direct neighborhood of the “core” and it’s elements, otherwise it does not become clear which elements belong to the periphery of which populations. If the graph becomes sufficiently complex, this is crucial. Given G, this operational procedure gives us the following results (cf. Fig. 8):

Fig. 8

Two population candidates given by the relatively high degree of their particular core element (node 4 and 6). Edges, which are part of a minimal cut (e and f) are excluded (red vertical lines)

• 1. Element 6 ($deg$ 4) is the core element. This is a clear and non-trivial result.

• 2. Element 7, 8 and 9 are PC’s core. Edge e and f are excluded from PC, because they involve minimal cuts. This however leads to a decline of $deg$ of element 6 $\left( {\deg 3} \right).$

• 3. Element with the next highest deg is element 4 deg 3) and its neighborhood the periphery; but because of the minimal cuts given by edge e and f, it is already part of a new population (a new core) and since e is excluded, it only has $\deg 2$.

• 4. Not specified, due to lack of complexity of G.

Application to a more complex distribution of interactions

The algorithm is applicable to any given distribution of elements in principle. For illustrative purposes, we will abandon our well-known graph G at this point and consider a more complex graph H. As we saw, the four-step operation can also be implemented in G (and leads to clear results), but the results are not as vivid, due to a lack of complexity.

Figure 9 shows a graph H with a random distribution of edges and elements. The clustering algorithm leads to the following results:

Fig. 9

A graph H with two major populations, each consisting of a core (fringes) and a periphery (dashed fringes) and two minor populations; all of them separated from each other by minimal cuts

• 1. Encircled nodes (both $\deg 6$) depict the two core elements.

• 2. Their particular neighborhood (blue and green fringe) indicates the cores of the two (equally mighty) populations.

• 3. Dashed-encircled nodes show peripheral elements (of $\deg 5$, $\deg 4$ and $\deg 3$). Their particular neighborhood constitutes the populations periphery (dashed blue and green fringes).

• 4. Vertical red lines cross out those edges, which are minimal cuts.

The boundaries of the four populations in H (two major ones each containing a core and a periphery as well as two minor ones below) are clearly given by the minimal cuts. Furthermore, we can now distinguish between a population’s core (direct neighborhood of core elements) and a population’s periphery (direct neighborhood of peripheral elements). Core and periphery are regions in the space of interactions. These regions can overlap, an element can be member of the core as well as of the periphery, as it is the case in some elements in H. I suggest counting these borderline cases as core elements, but either way it is clear to which population they belong—and that is what we set out to clarify. In principle, step 3 of the algorithm can be repeated until you arrive at all nodes with $\deg 2$. In practice, this is often not necessary to get clear populations given by the rate and density of their interactions, as Fig. 9 shows.

Reproduction, variation, selection: towards a dynamical analysis

The picture is not complete yet, because every evolutionary explanation has to provide a dynamical analysis of how these CIPC clusters evolve through time, where interactions form parent–offspring lineages, formally specifying variation, selection and reproduction. This is a crucial requirement for any evolutionary explanation, (biological or cultural alike) and up to this point, our formalism only provides a static, not a dynamical picture. In other words: we have to move from population structure to population dynamics.

In order to do so, let us introduce some basic notions from the domain of “evolutionary graph theory” (Nowak 2006, p. 123). As already outlined in the previous chapters the edges determine (competitive) interactions. The dynamics on the graph could describe (cultural or biological) evolution like the spread of new ideas or inventions. As Nowak (ibid.) indicates, individuals in central positions may be more influential than others. The extension to graphs that change over time is an important task but for reasons of space, I can only provide a very sketchy picture here.

Let again $G = (E,I) = (\{ 1,2, \ldots ,9\} ,\{ a,b,c,d,e,f,g,h,i,j\} )$ be our graph of interest at time $t_{1}$. We can introduce reproduction, variation and selection by comparing it to another graph $G^{\prime } = \left( {E^{\prime } ,I^{\prime } } \right)$ at time $t_{2}$ which is a result of G′s change in time. Figure 10 depicts this evolutionary development.

Fig. 10

The evolution of a graph G at t₁ to G′ at t₂. An evolutionary algorithm consisting of reproduction, variation and selection is established. Most interactions became reproduced (thicker lines), two new interactions appeared (*) as variations of the graph, some became negatively selected (dotted lines)

For reasons of simplicity, we only assume a slight change in the topology. The nodes $E = \{ {1,2, \ldots 9} \}$ stay the same while edges d and h disappear, i.e. become negatively selected (selection). Two new edges appear, namely k* and l* (variation). All other edges reappear in G′ (reproduction). The space of all possible states that the dynamical system can take is a large set of possible combinations within the maximal number of edges $\# I_{max}$. The latter can be calculated by the total number of nodes, $\# E$:

$$\# I_{max} = \# E \times \frac{\# E - 1}{2}$$

where for G we have $\# E = 9$ and therefore $\# I_{max} = 36$. Given a fixed number of nodes, there are $2^{{\# I_{max} }}$ total states, in our simple case already $2^{36} = 68 719 476 736$, and every such state is a possible graph G_i. All of these possibilities can be reached by the dynamical system, at least in principle. However, some graphs will be “fitter” than other ones, because they consist of more cohesive subgraphs, i.e. a nearly decomposable architecture (cf. “Near decomposability and avoiding the type-problem” section). We can formalize the evolution of the interactions within the changing network with a difference equation. The change in the system

$$\frac{{\Delta G_{t} }}{\Delta t} = \varphi \left( {G_{t} , \alpha } \right)$$

is a function $\varphi$ of the state of the system (G′s topology at time t) as well as a set of parameters $\alpha$, involving the relative fitness value of each possible Graph G_i.¹⁴ The fitness of a particular graph should somehow be tied to the cohesion of G′s subgraphs, i.e. the population candidates. Evolution selects those groupings, that have the largest cohesion. Mathematically speaking, those groupings are called “attractors”. At this point, a weighting function $w_{i}$ should also enter the picture (cf. “How to formalize the CIPC: the “cohesion index”” section, last paragraph), here belonging to the set of parameters $\alpha$.

In the following section, we will leave the abstract realm of graph-theory and clustering algorithms and investigate some possible applications.

Possible applications: providing foundations for the formalism

A crucial question of applicability will be: “How can interactions be quantified?” In general, how can the algorithm be applied “in the field”, to cases from sociocultural (and biological) evolution? Since the CIPC heavily relies on the particular strengths of interactions between agents (given by their number and density), any researcher needs some idea how to quantify them. Of course, it largely depends on what kind of causal interaction you are actually interested in in your study. There is a set of candidates that count as evolutionary relevant interactions (mating, caring, eating, growing, signaling…), cf. Stegenga (2016, p. 15), but this is only relevant for biological evolution. In cultural evolution, possibly any social interaction that has a possibility to proliferate can be an object of investigation. I will briefly mention four areas of research, where our formalism could be applied.

• 1. Games and graphs

Game Theory is a commonly used method in the social sciences.¹⁵ Interactions are called “strategies” in this research context. Normally, an agent (“player”) is faced with a decision-problem of some sort and the outcome of his actions depends heavily on how the other players act. In games of coordination, agents have to interact cooperatively, to maximize their utility. In evolutionary game theory (cf. footnote 16), these interactions can be quantified in a payoff matrix. The matrix shows the payoffs, in terms of the change in the fitness of one of the organisms as a result of the encounter, given all possible combinations of encounters that can take place in the population, i.e. the distribution of interactions that our formalism can interpret. It becomes clear, that if a certain interaction type becomes successful and leads to a fitness increase, the density of this particular interaction in a population will be greater. Game theory is usually taken as a paradigmatic case of “methodological individualism”, since it reduces social interactions to individual’s decisions and mostly focusses on the microlevel. This has already been criticized by proponents of “collectivism” in the philosophy of the social sciences, cf. Steele (2014, p. 203). We think that both—individualism and collectivism—are both crucial perspectives on social phenomena, focusing individuals on the one, and populations on the other hand. So maybe a good idea of providing a foundation for the formalism and thereby also bridging the gap between microevolutionary and macroevolutionary phenomena—i.e. individuals and populations—in cultural evolution and GD (cf. “Why does GD need a population concept?” section) is combining clustering algorithms with evolutionary game theory in such a way, that explanatory value is increased. My idea would be to show a particular social situation, where the macrolevel cluster could be seamlessly transferred into a specific microlevel game [similar as in “games in graphs”, cf. Nowak (2006, p. 139)]. However, a detailed description of such a model cannot be given here. The emergence of language systems and their conventional meaning have already been studied in the framework of evolutionary game theory, esp. in the case of “signaling games”, cf. Skyrms (2010) and these approaches have also been compared with “teleosemantics”, a classical approach in the evolution of language, cf. Baraghith (2019). This is a link to the next possible area of application.

• 2. Population structure in language evolution

Another potential area of application is the distribution of languages and language families, which have already been investigated in their evolutionary dynamics, cf. Mace and Holden (2005). Typically, speakers of a language (nodes) will linguistically interact (edges) with members of their language more frequently than to members of different languages and by this (not by internal features of the languages involved), one could group the speakers into language populations. Here, it also makes sense to speak of core and periphery of a language-population, as our algorithm suggests. The idea of cultural subsystems consisting of core and peripheral elements (as our algorithm indicates) is also well established in the context of cultural evolution or GD. As anthropologist Mace et al. (2005, p. 16) puts it, cultural core elements are very likely to be passed on intact and with a lower rate of mutation/variation, while peripheral elements tend to be diffused between cultures or—in our terms—cultural (meta-)populations. A vivid example are core concepts, resp. words of a natural language. They remain intact over many generations, sometimes for hundreds or even thousands of years. Why is that so? What could be the evolutionary explanation of such a phenomenon? Maybe one possible answer lies in the (game-theoretical) concept “ESS”, evolutionary stable strategy.¹⁶ Population cores may remain stable because they are related to behavior that has proven evolutionary stable. Another reason could be that core elements are subject to conformist bias, one major force acting on cultural transmission (Mesoudi 2011, p. 57) or pressure. In our framework, however, the core of a cultural population is richer in interactive density.

This idea can also be found in various investigations in linguistics, esp. about the population structure of languages and language families, cf. Yang (2009) or Lee et al. (2005). These recent approaches from linguistics emphasize that the role of the populations topology (e.g. given by an algorithm like ours) is critical in determining the degree of linguistic coherence and the language evolution, all of them assume some kind of formal measurement of the interaction-cohesion of the members of a language and how it influences language acquisition and evolution.

• 3. Economic interactions

Since the CIPC is a clear instantiation of “near decomposability” (cf. “Commonly accepted criteria for population membership” section), another field, where evolutionary ND systems are already investigated, is e.g. the framework of economic interactions, cf. Marengo et al. (2005).

• 4. Population based approaches in the social sciences

Another large area of application lies in “population-based approaches” in recent (philosophy of the) social sciences, cf. Longino (2014). They suggest that structural features of comparable populations of sociocultural agents have the power to explain social phenomena (such as “crime”), that no classical approach focusing mainly on the members’ individual features (genetic, neuronal, behavioral, social) can. Normally, these approaches do not put themselves under the standard of GD, which means that there could be some amount of unificatory potential, when linking these two different fields of research.

Conclusion and future outlook

In this paper, we investigated a possible population concept for the framework of generalized Darwinism (GD), the Causal Interactionist Population Concept (CIPC). Since this area of research still lacks a valid population concept this task became pressing for GD, in order to become a practicable research program, cf. Reydon and Scholz (2015). One strength of CIPC for this purpose lies in the external definition of what a population is (external at least from a member’s perspective): not the traits of the members determine who belongs to the population and who does not; all that matters are the interactions between the members. This approach must seem very attractive for proponents of GD, since it avoids (possibly problematic) discussions about (possibly typical) traits or features such as cultural genes (“memes”), or of (possibly mental) content, which members of the particular Darwinian population might (or might not) share. If pluralists like Stegenga (2016) are right to proclaim a conceptual (and formal) pluralism regarding population concepts in theoretical biology and philosophy of biology, we can take it for granted that this pluralistic view seems the best way to go for a theoretical framework like GD, as well. There, the complexity of different subfields of research is even higher than in biology. But if that is right and we actually should be more cautious about any narrow one-for-all-cases definition of what a population can be in GD’s terms—at least a small variety of proper population concepts are necessary for such a pluralistic view. This investigation tried to formulate one such candidate, namely the CIPC. It should not be understood as a strict definition of what a cultural population is, but one promising possibility. We tried to abstract away from the biological framework, by introducing a graph-theoretical model of the CIPC, which heavily builds on the distinction between external and internal interactions of any possible (meta-) population. We think of this as an interpretative generalization, which is not an analogy, and probably the best way to go for GD. A CIPC population is defined as a dense cluster of internal interactions, given by what we called cohesion index (CI). However, such a simple approach leads into some (mathematical) problems, namely the ambiguity of the best CIPC candidate, within a simple distribution of interactions. These issues can be eluded by introducing density measurements and cuts, which we did in “Challenges of the formalism” section. There, a final proposal for a clustering algorithm was introduced, which can be transferred into an evolutionary dynamic and applied to possibly many different cultural domains.

In a nutshell: This paper suggests rudiments of a formal approach for a macrolevel taxonomy for cultural evolution. It could serve as a basis for modelling macrolevel structures in GD systems but much work lies still ahead.