Learning from Paradoxes

Abstract

George Francis FitzGerald is well known to have proposed in 1889, three years before Lorentz, the (physical) contraction of bodies moving in the hypothetical ether, as an “explanation” the null result of the Michelson and Morley experiment. Less known is his proposal of an ether-drift experiment based on an electrostatic system. A simple charged condenser suspended by a wire would be subject to a torque due to the earth’s motion. The experiment was done by his pupil Trouton, with Noble, with null result. It was an important independent confirmation of the relativity principle, but it was substantially forgotten. It came back, under the form of a paradox, in the second half of the past century, usefully triggering an in-depth discussion on the electromagnetic energy and momentum flow in stationary systems, in which intuitively one thinks momentum should be zero, but it is not. The solution of the Trouton–Noble paradox, and similar ones, has led to a better understanding of the interplay between electromagnetic field and matter and to develop relevant examples for the university courses.

1 Introduction

The year 1905 is universally known as the birth year of Special Relativity. Indeed, four important papers were completed in that year, two by Poincaré (on June 5th [1] and July 23rd [2]) and two by A. Einstein (June 30th [3] and September 27th [4]). Much experimental and theoretical work had already been done, starting in the last decennia of the previous century, and, on the other hand, relevant aspects were still to be developed in the following years. In particular, while the geometry and the pseudo-Euclidean metric of the space–time (apart of the name given by Minkowski in 1908 [5]) and the relativistic kinematics had been substantially established in that year, the concepts of force, mass, energy and momentum had still to be fully understood. As it is practically always the case, the progress of physics is far from being linear, but rather proceeds through attempts that are not always successful, progress and setbacks, learning from errors. The historical literature on the field is vast and here I shall focus on a few episodes, the development and the solution of a few paradoxes, and how that contributed to understand the dynamics. In this section I shall start trying to summarise the concepts relevant for the following.

Today, every physicist knows that the mass m (including it being zero) of a freely moving particle is a Lorentz invariant, being the square root of the norm of the energy–momentum four-vector (p, iU/c)

$$\left( {mc^{2} } \right)^{2} = U^{2} - \left( {pc} \right)^{2}$$

(1)

and the relation between its energy and momentum

$${\mathbf{p}} = \frac{U}{{c^{2} }}{\mathbf{v}}$$

(2)

that, in case of massive particles (m ≠ 0), can be written as

$${\mathbf{p}} = m\gamma {\mathbf{v}}$$

(3)

with

$$\beta = \frac{v}{c}\quad \gamma = 1/\sqrt {1 - \beta^{2} }$$

(4)

However, to my knowledge [6], it was only after the second World War, with the textbook of Landau and Lifshitz [7] that the correct definition of “mass” became gradually established. Nevertheless, archaic concepts, born during the development phases of the theory, continue to appear in the literature, including school textbooks. The great Russian physicist Okun’ (1929–2015) spent the last decennia of his life, starting in 1989 [8], fighting against “the gang of four” as he said. Two “gangsters” have almost disappeared today: the “longitudinal mass” mγ³, which is the ratio of force and acceleration in the particular case they are parallel, and the “transverse mass” mγ, which is the analogous ratio in case the two are perpendicular to one another. The other two gangsters unfortunately are still on the loose. The first is the “relativistic mass” mγ that “varies with velocity”. This is not the mass, but, the constant c² apart, the energy. The second, consequence of the first, is the “rest mass” m₀, which is simply the mass, independently of being at rest or not. These concepts are particularly dangerous as they confuse simple issues. A fifth “mass”, which has now disappeared, was the “electromagnetic mass”. It was born when the hypothesis was advanced that the mass of the (classic) electron might be, at least partially, due, be equivalent we say now, to its electrostatic energy. The concept was first introduced by Thomson in 1881 [9].

It is well known today that the electromagnetic field contains momentum and energy with densities.

$${\mathbf{g}} = \varepsilon_{{0}} {\mathbf{E}} \times {\mathbf{B}};\quad w = \frac{{\varepsilon_{0} }}{2}E^{2} + \frac{1}{{2\mu_{0} }}B^{2}$$

(5)

It is also known, but often forgotten, that Eq. (5) does not define in general terms a four-vector, being it a column of the energy momentum tensor. Even more so, does not form a four-vector the expressions that we often use for the total field momentum and energy.

$${\mathbf{P}} = \int_{V} {\varepsilon_{0} {\mathbf{E}} \times {\mathbf{B}}\;dV } ;\quad U = \int_{V} {\left( {\frac{{\varepsilon_{0} }}{2}E^{2} + \frac{1}{{2\mu_{0} }}B^{2} } \right)dV}$$

(6)

given that the integration variable dV is not a four-scalar, nor are often such the integration limits.

Historically, it was Poincaré the first to propose in the year 1900 [10] the first Eq. (6), rewritten here in modern form, for the momentum of the electromagnetic field. The expression was also used to develop their (different) pre-relativistic theories of the electron by Max Abraham (1875–1922) [11,12,13] and Lorentz (1853–1928) [14] from 1902 (for a discussion see [15]).

More importantly, Poincaré himself in his Rendiconti paper on relativity, started from this expression [16] to find the relativistic generalisation of the second Newton law. He assumed the force to be equal to the time derivative of momentum, F = dp/dt which, by the way, is the form used by Newton rather than F = ma, with p given by Eq. (6). He established the correct equation [17]

$${\mathbf{F}} = m\gamma {\mathbf{a}} + m\gamma^{3} \left( {{\mathbf{a}} \cdot {{\varvec{\upbeta}}}} \right){{\varvec{\upbeta}}}$$

(7)

He then generalised the result proving that Eq. (7) is covariant under Lorentz transformations, not only, but also that this is the only possible expression of the force satisfying the relativity principle. Einstein in his 30th June 1905 paper trayed to generalise F = ma proposing an incorrect definition of the force. This led him to a wrong expression of the “transverse mass”, mγ² in place of mγ.

In the insight, we can immediately verify that the result of Poincaré is correct taking the time derivative of Eq. (3). This latter fundamental equation was unknown to Poincaré. It was found in 1906 by Max Planck in a paper [18] in which.

Therein the task is treated to determine the preferred form of the fundamental equations of mechanics, which take the place of the usual Newtonian equations of motion of a free mass point,…when the relativity principle should have general validity.

Starting from the correct expression of the momentum of a particle, Eq. (3), he reached the same result as Poincaré, the correct generalization of the second Newton law

$${\mathbf{F}} = \frac{{d{\mathbf{p}}}}{dt} = m\frac{d}{dt}\left( {\gamma {\mathbf{v}}} \right)$$

(8)

A further important contribution was delivered by M. Planck at the 1908 meeting of the Society of German Scientists and Physicians at Cologne [19]. His main effort in that period, in which the relativity theory was not yet completely developed, was the unification of different fields of physics. At the meeting he analysed the relations between electrodynamics and the principle of action and reaction. He stated that a unified definition of electromagnetic and mechanical momentum was possible assuming the validity of the Einstein theory of relativity. He established that the momentum per unit volume is equal to the energy flow per unit surface and unit time divided by the square of the speed of light. This definition of momentum provided the “real significance of the reaction principle”. The relation between energy flow and momentum density, already known for the electromagnetic field, was now completely general.

After this premise we can go to the main parts of this note.

I shall start in Sect. 2 discussing a proposal to test the ether drift made by George FitzGerald to his pupil Frederick Trouton in 1901, in the last year of his life. The motion of the Earth through the ether should produce a torque on a charged condenser, moving at an angle with the Earth velocity. The experiment was done two years later by Trouton with his pupil Noble, with a null result (Sect. 3). It was repeated with largely improved accuracy by Chase in 1926 (Sect. 4), again with a null result, triggered by claims made by Miller, a former pupil of Morley, to have detected an effect in a Michelson-Morley type of experiment. The absence of a torque in the Trouton and Noble experiment soon appeared as a paradox. Before discussing its solution in Sect. 6, I shall deal in Sect. 5 with the Lewis and Tolman paradox, which is conceptually similar, and easier to solve. Finally, in the following sections I shall summarise how the solutions of the paradoxes contributed to wider discussions and in-depth analyses. On one side, the attention of the community was brought on published, but substantially ignored, works showing that the common expressions of electromagnetic energy and momentum do not lead, in general, to a four-vector. On the other side, they led to a deeper understanding of these fundamental quantities.

2 George Francis FitzGerald

Before meeting George Francis Fitzgerald, I shall recall briefly the physics landscape of his time.

In the first decennia of the XIX century the wave nature of light was firmly established, starting from the two-slit interference experiment of Thomas Young (1773–1829) in 1801 in Britain and from the Augustin-Jean Fresnel (1788–1827) Mémoire of July 29th 1818 on the theory of diffraction, Couronné by the Académie de sciences in 1819. Then, being the light a wave, scientists assumed a medium had to exist in which luminous waves propagate, an all-pervasive substance that fills the space. Indeed, the known waves, like sound, did not propagate in absence of a medium. A ringing bell in an evacuated glass sphere could not be heard. As light reaches us from the farthest stars, the medium supporting the wave had to encompass the Earth and pervade the entire universe. It had to be extremely light and, considering that the speed of light was so large, also very rigid. It was called eather from Latin aetherium, simplified in ether, sometimes luminiferous ether, the light supporting one, when a distinction was needed from the other hypothetical substances imagined while developing the understanding of matter and heat.

However, since the previous century, the simple idea of an Earth moving in an ether stationary in the solar system was contradicted by facts. In 1727, the British astronomer James Bradley (1693–1762), having succeeded to improve the precision in the measurement of the stars positions by an order of magnitude, down to one arc-second, reported to the Royal Society the discovery of the “stellar aberration”. Due to the composition of the speed of light, which is not infinite, and the speed of the Earth, stars are not seen in their “real” positions, but at a distance from that of about 20’’, or 10^–4 rad, which changes direction during the year [20]. This, by the way, was historically the first proof of the Earth revolution. With insight, the “aberration coefficient” is equal to the ratio of the Earth orbital velocity and the velocity of light β_E = v_E/c = 10^–4. The observation informs us on the motion of Earth relative to that star, but does not tell anything on its absolute motion relative to the ether. The problem, for the existence of the ether, was that, as the aberrations for more stars were measured, it was found to be the same for all of them, independently of their distance and of their position. Ad hoc hypotheses where advanced, called of the ether drag, assuming that the Erath would drag, at least to some degree, the ether in its motion. I shall not deal further with this period, which is masterfully narrated by E. Whittaker (1873–1956) in his History of the theories of aether and electromagnetism [21].

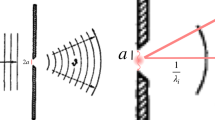
After the completion of the electromagnetic theory by Maxwell in 1865, it became increasing clear that the possible absolute motion of the Earth in an ether assumed at rest in the solar system had to be tested with laboratory experiments. They were called ether drift experiments. However, differently from the light coming from a star that travels in a single direction, in any experiment on Earth the light has necessarily to travel back and forth on a closed path. It is easy to see that this implies that the searched effect is of the second order of the aberration, namely proportional to β_E squared, which is 10^–8. This looked impossible to detect, including to Maxwell, but a young officer of the American Navy, Albert Abraham Michelson (1852–1931), then in Germany, accepted the challenge and performed the to become famous experiment in the basement of the Astrophysicalishes Observatorium in Postdam in 1881 [22]. The result was null, and Michelson concluded that “the result of the hypothesis of a stationary ether is shown to be incorrect.”

However, the sensitivity of the experiment was just sufficient to detect an ether drift if it existed, and Michelson, back in the USA, designed with Edward Morley (1838–1923) a ten times more sensitive interferometer in Cleveland, Ohio, in 1887, again with a null result [23].

We can now go and meet George Francis FitzGerald (1851–1901). He was born in Dublin, Ireland, on the 3^rd of August 1851. His father, William, was a minister of the Irish Protestant Church. Together with his siblings George was tutored home. He entered Trinity College Dublin at the age of 16 to study mathematics and experimental sciences and graduated in 1871. He spent the following 6 years in preparation to compete for a Trinity College Fellowship, studying in depth the major mathematicians like Lagrange, Laplace and Hamilton and becoming fascinated by the Electricity and Magnetism of Maxwell (1873). He won the Fellowship and became a tutor at Trinity College in 1877 and professor of natural and experimental philosophy in 1881. As a brilliant lecturer and physicist, he contributed, in particular, to confirmations and extensions of the electromagnetic theory of Maxwell. In this frame he imagined an electrical oscillator to generate electromagnetic waves, but did not put that in practice.

He is universally known for is his proposal, published in a letter to Science in 1889, to try to save the ether after the Michelson-Morley experiment. The idea was that the arm of the interferometer parallel to the velocity relative to the ether would contract.

I would suggest that almost the only hypothesis that could reconcile this opposition is that the lengths of material bodies changes, according as they are moving through the ether or across it, by an amount depending on the square of the ratio of their velocities to that of light. [24]

The same “trick” was proposed independently by Lorentz in 1892 [25], without knowing of the Science letter. In November 1894 he wrote to FitzGerald to ask if he had ever published anything on the subject. FitzGerald replied that he recalled writing a letter to Science but he did not know if it had ever been published. He was glad to hear that the great Lorentz had the same idea, also because he had been “rather laughed at for my view over here” [26]. Honestly, Lorentz recognized the FitzGerald contribution in 1895 in a footnote in his next, very important, paper on electron theory [27]. The idea is now known as the FitzGerald-Lorentz contraction. We now know they were wrong in assuming the contraction as a physical rather than purely geometrical effect, but we should also know that the route to new physics goes through errors. In this case this amounted to no less than the discovery of the Lorentz transformations.

The conclusions, namely, in modern language, the statement of validity of the relativity principle, were drawn already in 1899 by Poincaré in his lectures. As usual for him, he carefully and critically discussed the existing astronomical observations and experiments that had failed to detect the absolute motion of the Earth, as we summarised above. After having presented the “trick” of the FitzGerald-Lorentz contraction, he concludes:

This strange property looks like a true “coupe de pouce” [a push, like giving a good word for someone to pass an exam] given by nature to forbid the possibility to detect the absolute motion of the Earth with optical phenomena. Of this I am not satisfied and I think I have to tell my opinion: I believe to be highly probable that the optical phenomena depend only on the movements of the material bodies that are present, luminous sources or optical apparatuses, and this not only for quantities of the order of the square or of the cube of the aberration, but rigorously [emphasis of P.]. As the measurements will become more exact, this principle will be verified with increasing precision.

Will it be necessary a new coupe de pouce, a new hypothesis, at each approximation? Obviously not: a well-done theory will need to demonstrate this principle in one shot only with a complete rigor [28].

The “principle” is obviously the relativity principle, as Poincaré will call it, first, in 1904 [29], having used in place the term “principle of the relative motion” since 1895 [30]. The “well-done” theory, as we well know, will come in 1905. However, the idea of the contraction as a physical effect was not to disappear for many years to come.

The still pre-relativistic contribution of FitzGerald we are interested in here was given in 1901, the last of his life, with a suggestion to his assistant Frederick Trouton (1863–1927) for a possible electrostatic test of the motion through the ether [31]. The idea was still in the general framework of the contraction. If a plane capacitor is freely suspended with its plates making an angle y with the “direction of the ether drift”, different from 0˚ and from 90˚, one should observe a couple acting on the system. The argument goes as follows.

Consider a parallel plate condenser, with the distance d between the plates much smaller than their diameter. Let C be its capacitance. Let us charge it to the potential difference ∆φ. Consider first the capacitor at rest. The electric field E is present between the plates and is zero outside, the magnetic field B is zero everywhere.

If the volume between the plates is V, the energy of the system is electrostatic only

$$U_{0} = \frac{{\varepsilon_{0} }}{2}E^{2} V = \frac{1}{2}C\Delta \varphi^{2}$$

(9)

If now the capacitor moves with a velocity v perpendicular to the plates, there will be still no net electric current, because the effects of the positive and negative charges neutralise each other and the magnetic field will again be zero. In this non-relativistic argument, the electric field will be the same as at rest, and the same will be the energy.

If v is parallel to the plates, E is still the same as at rest, but the magnetic field will not be zero, but B = v × E/c². The energy of the system, if β = v/c, is given by

$$U_{p} = \frac{{\varepsilon_{0} }}{2}\left( {E^{2} + c^{2} B^{2} } \right)V = \frac{{\varepsilon_{0} }}{2}\left( {1 + \beta^{2} } \right)E^{2} V = \left( {1 + \beta^{2} } \right)U_{0}$$

(10)

that is larger than in the perpendicular configuration. Consequently a torque should exist on the condenser tending to rotate it towards the lower energy position. To calculate this couple, consider the energy of the capacitor for a generic angle ψ. This is U = U₀ (1 +β ²) cos²2ψ. We find the couple using the principle of virtual works.¹ Noticing that only the magnetic energy depends on y, we have

$$\tau = - \frac{dU}{{d\psi }} = U_{0} \beta^{2} {\text{sin}}2\psi = \frac{1}{2}\varepsilon_{0} \beta^{2} E^{2} V{\text{sin}}2\psi = \frac{1}{2}C\Delta \varphi^{2} \beta^{2} {\text{sin}}2\psi$$

(11)

We see again that the effect is proportional to β², and maximum at ψ= 45˚. For capacitances of the order of 10 pF and potential differences of the order of the kilovolt, the couple expected for the Earth orbital motion (β = 10^–4) is in the order of 10^–15–10^–14 Nm, which is small, but not too small to be measurable at the time.

3 The Trouton and Noble Experiment

The experiment was performed for the first time in 1903 by Trouton, who had moved to London to become professor of physics at the University College in 1902, with his assistant Noble. The results were read to the Royal Society of London on June 18th 1903 and published as a short note [32] in the Proceedings of the Society and, with a more complete description, in the Philosophical Transactions of the Society [33].

The apparatus is shown in Fig. 1. The condenser, whose construction is accurately described, is suspended with a 37 cm long phosphor bronze strip PA, “the finest that could be obtained”. The circuit was closed with a thin platinum wire (6 mills) beneath the condenser dipping in a conducting liquid (sulfuric acid). To avoid effects of air currents or draughts, the condenser was fitted in a smooth colloidal ball. The ball was covered by gilt paint and earthed. The authors carefully discuss the shielding and mechanical precautions used to “practically eliminate all electrostatic disturbances”.

A plane mirror [P] was attached to the condenser, this was viewed by means of a telescope and scale, through small mica windows in the zinc coverings [33].

Fig. 1

The suspended condenser of the Trouton an Noble experiment [33]

To determine the unperturbed position of the condenser it was set in oscillation uncharged and readings were taken every quarter of a minute, being the period about 8 min long (due to the large moment of inertia of the condenser). During the following measurements the zero on the scale did not change by more than 0.5 mm. Similar procedure was used to measure the deviation with the charged condenser. A total of eleven measurements were taken from March 9 to 18 at different hours in order to

If condenser be hung with its plane north south, then at about 12 o'clock in the day there would be no couple tending to turn it, because the aether drift due to the earth's motion in its orbit round the sun is at right angles to the plane of the condenser; on the other band, at any other hour, say 3 o'clock, there would be a couple making itself felt by a tendency to rotate the plane of the condenser into the position at right angles to the drift [33].

After having described how they calculated the deflections expected due to both the diurnal and annual motion of the Earth relative to a stationary aether, the authors present a table with the experimental results, stating that

These were observations taken after many months of experience with the apparatus and were considered by us as conclusive against there being any such effect as we were seeking…

The largest observed deflection, 0.36 cm, barely exceeds 5 per cent of the calculated deflection 6.8 cm…

Dedicated tests were made to check the nature of the observed small deviations, coming to the conclusion that the effect observed was the result of residual electrostatic action, and could in no way be attributed to the relative motion of the earth and the aether.

This was a very important result, but the authors did not draw the conclusions we, looking with insight, would have expected. Rather they add

There is no doubt that the result is a purely negative one. As the energy of the magnetic field, if it exists (and from our present point of view we must suppose it does), must come from somewhere, we are driven to the conclusion that the electrostatic energy of a charged condenser must diminish by the amount N(u/v)², when moving with a velocity u at right angles to its electrostatic lines of force, where N is the electrostatic energy [and u is the speed of light].

Clearly, we are still in pre-relativistic times, but the authors already raise the problem of understanding the reasons of their null result. As a matter of fact, the reason is far from trivial and the effect became known as the Trouton and Noble paradox. We shall come back to the solution in 6.

4 The Carl Chase Experiment

After having worked with Michelson in the year 1887 in their famous experiment, Edward W. Morley (1838–1923), still in Cleveland, developed a programme finalised to test the FitzGerald-Lorentz contraction, with his student Dayton Clarence Miller (1866–1941). In the first 1900s they built an interferometer about four time more sensitive than the Michelson-Morley one. To check if the contraction could depend on the material, they started testing whether changing the material of the interferometer base, like wood or steel, would make any difference. But they did not reach any significant results. In 1905–1906, having the doubt that their experiment would only prove “that the ether in a certain basement room is carried along with it”, moved to the nearby Euclid Hights about 870 feet a. s. l.. Observations apparently showed a positive effect, one tenth of the value expected if due to the Earth orbital motion in the ether. However, spurious temperature effects could not be excluded.

In 1906 Morley retired, but in 1921 Miller resumed the effort, now moving the interferometer to the Mount Wilson Observatory. His basic idea was that, while the Michelson-Morley experiment had searched specifically for the motion of the Earth in an ether assumed to be stagnant in the solar system, a search independent of this assumption was worthwhile.

Miller published a full review of his efforts in 1925 [34]. His conclusions were two. First, the data are fully consistent with the conclusion of Michelson-Morley, no ether drift due to the orbital velocity of the Earth was detected. Second, a positive effect was claimed, consisting in a

Systematic displacement of the interferometer fringes corresponding to a constant relative motion of the earth in the ether at this observatory of ten kilometers per second; and that the variations in the direction and magnitude of the indicated motion are exactly such as would be produced by a constant motion of the solar system in space, with a velocity of two hundred kilometers, or more, per second, towards an apex in the constellation of Draco, near the pole of the ecliptic, which has a right ascension of 262˚ and a declination of +65˚.

Quite a strange effect indeed, and the author notices that

In order to account for these effects as the result of an ether drift, it seems necessary to assume, in effect, the earth drags the ether so that the apparent relative motion at the point of observation is reduced from two hundred, or more, to ten kilometers per second, and further that this displaces the apparent azimuth of the motion about 45˚ to the west of north.

This was twenty years after the special relativity theory. From the experimental point of view, one notices the absence of a proper discussion of the significance of the claim, as determined by the experimental uncertainties, both statistical and, more important, systematic ones. The measured data points are reported without any error bar. The discussion of the agreement of the “best fit” curves to the experimental data is purely qualitative. No statistical test against the null hypothesis was done, even if, e. g., the chi-square test had already been proposed since 25 years [35].

In any case, an experimental control with an independent method was desirable, and Carl T. Chase (1902–1987), then a graduate student at the California Institute of Technology, in 1926 set to repeat the Trouton and Noble experiment [36]

using more sensitive apparatus and continuing the observations over longer periods of time, to see how negative the results of Trouton and Noble really were. They observed merely a few deflections each time the experiment was tried.

Chase starts quoting that a similar experiment had been performed in the previous year by R. Tomaschek [37], with a claimed sensitivity of 10 km/s and with a null result. However, he states, it has been found that there were serious sources of error in the apparatus that would have produced a negative result in any case.

The first source of systematic error was the contact of the lower thin wire dipping in a solution of sulfuric acid. Would the frictional forces due to the surface tension of the liquid cause a couple comparable to that possibly due to the earth motion? To answer this question, Chase, having dipped the wire 2 mm deep in the solution, tried to turn the upper end of the upper wire, finding it could be turned through two or three complete revolutions without resulting in motion of the condenser. Clearly a rotation of a few degrees expected for an earth velocity of 10 km/s could not be detected.

The second issue was on how the charging high voltage had been generated, namely by a small static machine, in a way that makes it questionable the stability of the potential. This potential source of systematic uncertainty had not been discussed by Tomaschek.

The first improvement by Chase was to design the apparatus, shown in Fig. 2, as symmetric as possible, both axially and between in its lower and upper parts. The upper and lower connections were done with the same phosphor-bronze wire of 15 µm diameter. No liquid was used for the lower connection, avoiding any possible surface tension spurious couple. The oscillation period was reduced from the 8 min of the previous experiments to 40’’, by employing a much lighter condenser. This was built as a pile of 60 aluminium discs of 2 cm diameter separated by mica discs, resulting in a capacity of 40 pF. When set in oscillations, the system was able to continue for 20 to 30 min, allowing more statistically accurate measurements of the displacements. For symmetry, the mirror was installed on the lower wire.

Fig. 2

The Chase apparatus for his Trouton–Noble experiment

The potential, 600 V, was supplied by batteries (to guarantee stability), in series with a generator. The applied voltage was controlled and kept constant within one half of one percent, the limit of accuracy of the calibration of the voltage scale. The apparatus was enclosed in a metal structure serving not only as an electrostatic shield but also to eliminate disturbances from convection currents and to guarantee, with its large heat capacity, stable temperature conditions. The temperature, controlled every hour, was stable within 1 °C.

Chase performed several data taking runs, each 24 h long, taking a measurement every 5′. In each observation he measured the rest deflection with the condenser uncharged reading 5 (3 on one side + 2 on the other one) oscillation maxima and similarly with the charged condenser (3 min after having applied the voltage). Figure 3 shows, as an example the results of the April 24–25 1926 run. The curve shows the expectation assuming the Miller claim to be correct. Clearly it is not.

Fig. 3

Results of one measurements run of Chase. The curve shows the expectations assuming the 1925 claim by Miller to be correct

The authors notices that the smooth decrease with time of the deflection, is due to the elastic fatigue of the oscillating suspension wires. He quotes that already Lord Kelvin had shown that a suspension wire becomes increasingly stiffer when working. It will recover when at rest for some time. The small local maxima and minima appear only random in the different runs and would correspond to a velocity of 2 km/s.

The mean of several runs is nearly a straight line, with no deviation corresponding to a velocity greater than 1 km/s. If the size of the deflection must be divided by the dielectric constant as mentioned in the introduction [where it is mentioned that some authors claim that the r.h.s. of our Eq. (11) should be divided by the dielectric constant of the condenser], the greatest velocity that could remain undetected in any one run of twenty-four hours would be 5.5 km/s and in the mean of several runs, 4 km/s.

Experimentally, a clear progress can be seen, the sensitivity is now properly discussed, after having carefully studied and eliminated the sources of error.

5 The Lewis and Tolman Paradox and Its Solution

Before discussing the Trouton and Noble paradox, we will deal with a similar one, which is somewhat simpler to interpret. It appeared in the 1909 paper “The principle of relativity, and non-Newtonian mechanics”, by Lewis and Tolman [38], in which the authors propose an approach to relativity independent of electromagnetism. Their theory is wrong, but it was quite influential. In particular, the authors are among the main responsible of forming the public opinion on the misleading concepts of relativistic mass and rest mass. Let me briefly recall on purpose that Lewis, then an associate professor of physical chemistry at the MIT, Boston, already in 1908 published a paper [39] in which he assumed the validity of the relativity principle and

In the following pages I shall attempt to show that we may construct a simple system of mechanics which is consistent with all known experimental facts, and which rests upon the assumption of the truth of the three great conservation laws, ​namely, the law of conservation of energy, the law of conservation of mass, and the law of conservation of momentum. To these we may add, if we will, the law of conservation of electricity.

One of his assumption is clearly wrong, mass is not a conserved quantity. Here he defines the momentum as p = mv, stating that m, given by m₀g, is the mass and m₀ the rest mass. Even more explicit was Tolman [40] in 1912, then assistant professor of physical chemistry at the University of Cincinnati. He claimed once more that the mass is a conserved quantity and that as such it cannot depend on the direction (sic!). Consequently one should not talk of transverse and longitudinal mass. On the contrary

It has been believed by Professor Lewis and the writer, that in general, without respect to direction, the expression ${m}_{0}=1/\sqrt{1-{u}^{2}/{c}^{2}}$ is best suited for THE mass of a moving body.

We see how seven years after 1905, the concept of mass was still quite confused at least in some authors.

Of the 1909 Lewis and Tolman above quoted article, that moves on the same lines, we are interested here in what will become known as the “Lewis and Tolman paradox”.

Consider a rigid lever ABC whose arms are equal and perpendicular, and forces F₁ applied in A and F₂ applied in C, of equal magnitude F, in directions parallel to BC and BA respectively. The authors state that the system is in equilibrium. To be precise, the authors should have specified that a frictionless pivot in B holds the system on a fixed support. In Fig. 4 a) I included the force made by the pivot on the lever, decomposed in its components in the directions of the arms. Under these condition both the total force and the total torque on the lever are zero and the system is in equilibrium.

Fig. 4

a The lever of Lewis and Tolman in its rest frame. b The same when moving at speed v in the x direction

The authors write:

Now let us assume that the whole system is in motion with velocity v in the direction BC. Obviously, merely by making such an assumption we cannot cause the lever to turn, nevertheless we must now regard the length BC as shortened in the ratio $\sqrt{1-{\beta }^{2}}/1$ (where β = v/c) while AB has the same length as at rest. We must therefore conclude that to maintain equilibrium the force at A must be less than the force at C in the same ratio. We thus see that in a moving system unit force in the longitudinal direction is smaller than unit transverse force in the ratio $\sqrt{1-{\beta }^{2}}/1$.

Clearly the argument is wrong, it is the force in C, namely that perpendicular to the velocity, to be smaller, when the system is in motion, by a factor $\sqrt{1-{\beta }^{2}}$, while that in A does not change, as in Fig. 4b). Consequently, the support exerts on the lever a torque, of direction perpendicular to the plane and value

$$\tau_{z} = - Fa + \frac{F}{\gamma }\frac{a}{\gamma } = Fa\left( {1 - \beta^{2} - 1} \right) = - Fa\beta^{2}$$

(12)

Apparently, then, the equilibrium is lost. Even if the authors did not see it, this is known as the Lewis and Tolman paradox. Notice that the effect is proportional to β².

The paradox was solved by von Laue in 1911 [41], who had been told by Sommerfeld of the mistake. When the system is in motion with velocity v in the x direction, the force in B does on the lever a work per unit time equal to w_B = –Fv, and the force in A the work per unit time w_A =  + Fv. The other forces do no work, so that the total power given to the system by the support is zero. However, power enters the lever in A and leaves it in a different point, namely B, and, as a consequence, there is an energy flux Φ = Fv/S′ along the side perpendicular to the motion (where S′ is its section in the moving frame).

Apparently, Lewis and Tolman had not read the above mentioned work of Planck [19]. In their case, the momentum density corresponding to the energy flux, which is in the y direction, is g_y = –Fv/(S′c²). Multiplying by the volume, S’a, we get the total linear momentum P_y = g_yS′a = –Fav/c². This moving linear momentum corresponds to an angular momentum relative to the fixed origin O in Fig. 4b, in the direction z perpendicular to the plane, equal to L_z = –(Fav/c²)vt. We see that the total angular momentum is not constant, but varies with time. Consequently a non-zero torque must act on the system, namely

$$\frac{{dL_{z} }}{dt} = - \frac{Fav}{{c^{2} }}v = - Fa\beta^{2} = \tau_{z}$$

(13)

that is exactly the torque in Eq. (9). We see that the torque on the bar is a necessary consequence of the relativity principle.

An important point to be stressed is that the system has two interacting components: the support acting on the lever with the couple of Eq. (12) and the lever, which acts on the support with an equal and opposite couple.

6 The Trouton–Noble Paradox

The effect discussed in Sect. 2, namely that a charged condenser is subject to a couple when moving at a velocity v, can be considered independently of the ether-drift. We just think to be looking at a charged condenser moving with a constant, but arbitrary, velocity v in an inertial reference frame. This is the Trouton–Noble paradox. Similarly to the Lewis and Tolman one, the condenser in equilibrium when at rest should apparently rotate in when in motion. Is the solution due to having considered the problem non-relativistically?.

Let Σ₀ be the condenser at rest reference frame and Σ the frame in which it is in motion. Working in Σ the we start considering again the two extreme cases of v parallel and normal to the plates. In place of Eq. (10) we have now, with V₀ and E₀ volume and electric filed at rest

$$U_{p} = \frac{{\varepsilon_{0} }}{2}\left( {\gamma^{2} E_{0}^{2} + \gamma^{2} \beta^{2} E_{0}^{2} } \right)V_{0} /\gamma = \gamma \left( {1 + \beta^{2} } \right)U_{0}$$

(14)

If the velocity is normal to the plates, the magnetic field is zero, the electric field, being normal to the boost is the same as at rest and the only change is that of the volume. We have

$$U_{n} = \frac{{\varepsilon_{0} }}{2}\frac{{E_{0}^{2} }}{\gamma }V_{0} = U_{0} /\gamma$$

(15)

We have still U_p > U_n, and that is even worth, because the difference U_p–U_n that was β²U₀, is now, in the small velocity approximation, twice as big, namely 2 β²U₀. Consequently a couple should still exist acting on the condenser when oriented at a generic angle with v. The relation between the angles in the two frames is tan ψ = γ tan ψ₀ and between the volumes V = V₀/γ. Lorentz transforming also the fields we find that the energy is

$$U\left( \psi \right) = \frac{{U_{0} }}{\gamma }\left( {1 + \frac{{2\gamma^{2} \beta^{2} {\text{cos}}^{2} \psi }}{{1 - \beta^{2} {\text{sin}}^{2} \psi }}} \right)$$

(16)

Taking the derivative we get

$$\tau = - \frac{\partial U\left( \psi \right)}{{\partial \psi }} = \frac{{2U_{0} \beta^{2} }}{\gamma }\frac{\sin 2\psi }{{\left( {1 - \beta^{2} {\text{sin}}^{2} \psi } \right)^{2} }}$$

(17)

That for small velocities becomes

$$\tau \sim \frac{{2U_{0} \beta^{2} }}{\gamma }\sin 2\psi = \varepsilon_{0} \beta^{2} E_{0}^{2} V_{0} {\text{sin}}2\psi$$

(18)

which is, again, twice the non-relativistic result of Eq. (11)

The simplest solution of the paradox is analogous to that we found for the Lewis-Tolman one. Here the two interacting components of the system are the electromagnetic field, analogous to the lever, and the mechanical system, namely the mechanical structure of the condenser, analogous to the support of the lever. In the rest frame Σ₀ the magnetic field is zero and, as a consequence, the Poynting vector, the electromagnetic energy flux and the momentum density are zero. When the condenser is moving as seen in the frame Σ there is an energy flow parallel to the plates given by the Poynting vector, and, consequently, an electromagnetic momentum density in the space between the plates, given by g = ε₀ E × B, as shown in Fig. 5. Notice that, being B proportional to v × E, and being E perpendicular to the plates, the magnitude of the magnetic field, and hence of the momentum density, depends on the angle, varying as cos${\Psi}$.

Fig. 5

The condenser and the fields in the Σ frame

Again, similarly to the Lewis-Tolman case, the electromagnetic momentum P_e = gV moves with a velocity v, with a consequent time variation of the electromagnetic angular momentum dL_e/dt = v × P_e relative to a fixed pole (the footer e is to indicate it being electromagnetic). The cross product gives a factor siny in its angle dependence, which, together to the above mentioned cosy in the magnitude of the magnetic field, gives an overall siny cosy factor corresponding to sin2ψ in Eq. (18). The existence of an acting momentum

$${{\varvec{\uptau}}} = - \frac{{d{\mathbf{L}}_{{\varvec{e}}} }}{dt}$$

(19)

appears again to be absolutely necessary.

Which is the agent of the couple? In analogy to the Lewis-Tolman case, it is the other component of the system, now the mechanical structure of the capacitor. As a matter of fact, the mechanical couples can be thought to be two. The first is made by the mechanical forces made by the dielectric to keep the two plates, which electrically attract one another, at a fixed distance. In Fig. 6, in the Σ₀ frame we represent this action as due to a transversal rigid bar. The footers m indicate that the forces are due to matter, the apex ˚ that we are in the rest frame.

Fig. 6

Scheme of the mechanical forces in the rest frame. a₀ is the length of the plates, d⁰ is their separation

In addition, the charges on each of the surfaces repel each other, expanding longitudinally the plates (they would do so if the plates were elastic). Following Ref. [42]. we represent in Fig. 6 the couple as due to a longitudinal rigid bar keeping the extremes of the plates at fixed distance.

The force normal to the plates is easily calculated. If σ₀ is the surface charge density and A₀ = bd⁰ is the plates area, we have

$$F_{m,1}^{0} = \frac{{\sigma_{0}^{2} }}{{2\varepsilon_{0} }}A_{0} = \frac{{\varepsilon_{0} }}{2}E_{0}^{2} A_{0}$$

(20)

More work is taken by the calculation of the (two equal) forces parallel to the plates. The result for their sum is exactly the same

$$F_{m,2}^{0} = \frac{{\varepsilon_{0} }}{2}E_{0}^{2} A_{0}$$

(21)

We see that in Σ₀ both couples have zero arm and the total momentum is zero. Moving now to reference Σ, the geometrical distances parallel to the boost and the components of the forces normal to the boost, contract by a factor g and both couples have non-zero momentum, as shown in Fig. 7.

Fig. 7

Scheme of the mechanical forces in the Σ frame. a Transverse bar, b Longitudinal bar

The momentum of the couple due to the transverse bar is

$$\tau_{1} = \frac{{\varepsilon_{0} }}{2}E_{0}^{2} A_{0} d_{0} \beta^{2} \sin 2\psi_{0} = \frac{{\varepsilon_{0} }}{2}E_{0}^{2} V_{0} \beta^{2} \sin 2\psi_{0}$$

(22)

which is one half of what we need.

The momentum of the couple due to the longitudinal bar is

$$\tau_{2} = \varepsilon_{0} E_{0}^{2} bd_{0} a_{0} \beta^{2} \sin \psi_{0} \cos \psi_{0} = \frac{{\varepsilon_{0} }}{2}E_{0}^{2} V_{0} \beta^{2} \sin 2\psi_{0}$$

(23)

That gives us the other half, and finally we have that the mechanical momentum acting on the electromagnetic component of the system is

$$\tau = \tau_{1} + \tau_{2} = \varepsilon_{0} E_{0}^{2} V_{0} \beta^{2} \sin 2\psi_{0}$$

(24)

which is equal to Eq. (18).

In conclusion, both the Lewis and Tolman and the Trouton and Noble paradoxes can be understood observing that the apparently absurd torque appearing when the systems are moving is not at all absurd, but is exactly what is needed to take into account the momentum corresponding to an energy flux in one of the components of the system, the lever or the condenser electromagnetic field.

7 Other Useful Paradoxes

In our discussion of the Trouton and Noble experiment we started from the pre-relativistic idea of FitzGerald that the energy of a condenser moving with velocity v depends on the angle between the plates and that velocity. In special relativity, however, the energy of a system is the fourth (time) component of a four-vector, which, as such, transforms form one frame to another independently of the direction of the boost. Namely, if U₀ is the energy in the rest frame, it should be U₀γ in the moving frame for any orientation and, consequently, the torque on the condenser should be zero.

The reason of this apparent paradox is that, as recalled in the Introduction, the usual definitions, Eq. (6) of the electromagnetic field energy and momentum do not define a four-vector. The issue is fully discussed in the Fritz Rohrlich book Classical charged particles [43]. Here I summarise the most relevant points.

We start considering the energy–momentum tensor of the system, which is the sum of an electromagnetic and a mechanical part. We then write

$$T_{ik} = T_{ik}^{e} + T_{ik}^{m}$$

(25)

If the total system is isolated the energy and momentum conservation is written as

$$\partial_{k} T_{ik} = 0$$

(26)

However, in general, the divergences of both components are not separately zero. As shown by Rohrlich, only if ${\partial }_{k}{T}_{ik}^{e}=0$ the usual definitions of Eq. (6) give a four-vector. This is the case of electromagnetic radiation in absence of sources, but not our case. The general covariant expressions are [44]

$$\begin{gathered} {\mathbf{P}}^{e} = \frac{{\gamma^{2} }}{c}\varepsilon_{0} \mathop \smallint \limits_{V}^{{}} \left[ {c {\mathbf{E}} \times {\mathbf{B}} + \left( {{{\varvec{\upbeta}}} \cdot {\mathbf{E}}} \right) {\mathbf{E}} + c^{2} \left( {{{\varvec{\upbeta}}} \cdot {\mathbf{B}}} \right) {\mathbf{B}} - \frac{1}{2}{{\varvec{\upbeta}}} \left( { E^{2} + c^{2} B^{2} } \right)} \right]dV \hfill \\ U^{e} = \gamma^{2} \varepsilon_{0} \mathop \smallint \limits_{V}^{{}} \left[ { {\mathbf{v}} \cdot {\mathbf{E}} \times {\mathbf{B}} + \frac{1}{2}\left( {E^{2} + c^{2} B^{2} } \right)} \right]dV \hfill \\ \end{gathered}$$

(27)

The expressions simplify considerably for “electrostatic” systems, as it is our one. Such systems are defined as those for which a “rest” reference frame exists, in which the field is purely electrostatic. Equations (27) become

$${\mathbf{P}}^{e} = \frac{{\gamma^{2} }}{c}\varepsilon_{0} {{\varvec{\upbeta}}}\mathop \smallint \limits_{V}^{{}} \left( {E^{2} - c^{2} B^{2} } \right)dV;\quad U^{e} = \frac{{\gamma^{2} }}{2}\varepsilon_{0} \mathop \smallint \limits_{V}^{{}} \left( {E^{2} - c^{2} B^{2} } \right)dV$$

(28)

In the rest frame Σ₀, P^e = 0 and ${U}_{0}^{e}=\frac{{\varepsilon }_{0}}{2}\int \left({E}^{2}-{c}^{2}{B}^{2}\right)dV$. Lorentz transforming to Σ, we have immediately

$${\mathbf{P}}^{e} = \gamma U_{0}^{e} {\text{v}};\quad U^{e} = \gamma U_{0}^{e}$$

(29)

The energy is independent of the orientation of the condenser. The momentum acting on the condenser is zero.

For completeness, we observe that, being the electromagnetic part P^e defined as a four-momentum, and the total one P^e + P^m being obviously also so, the mechanical part P^m is a four-momentum too. It can be shown [45] that in this case P^m = 0.

The solution of the Trouton–Noble paradox has been amply discussed in the literature, especially in view of its relevance in teaching electromagnetism. There have been basically two types of solutions.

The explanations of the first type, the most frequent ones, start from the common non-covariant definition of the electromagnetic energy and momentum of Eq. (6) [39, 40, 46]. The positive aspect of this approach is that it allows a deep understanding of the interplay between electromagnetic and non-electromagnetic components. We did that in §6, in the simplest way, for this reason. And for this reason the discussion of the paradox appears in the literature to elucidate concepts like the “hidden momentum”, a term introduced by W. Shockley in 1967 [47], and the solution of the “4/3 paradox”. I shall give some hints below. On the other hand, these solutions require quite a lot of ingenuity to identify and calculate correctly all the non-electromagnetic contributions. This may be highly non trivial and may lead to errors.

The second type of explanations relays on the use, advocated by Rohrlich, of the covariant definitions, of which Eq. (28) are for the special case of the electrostatic systems [41,42,43, 48,49,50,51], namely when a rest frame exists, in which the momentum density is g = 0. At the small price of using unfamiliar expressions, the main advantage is that the approach leads to simple and clear solutions, as in the example we showed at the end of the last section. On the other hand, the insight in the non-electromagnetic physics tends to be lost.

It was just along these lines that R. Feynman introduced discussions of examples, like the “Feynman disk paradox”, to illustrate to the students the concepts of energy flux and momentum density in stationary electromagnetic fields [52]. Hidden momentum and hidden angular momentum have been amply discussed in the literature, in the most different physical circumstances, of which examples are [53,54,55,56,57,58,59,60,61,62]

Historically, the earliest origin of the 4/3 problem should be traced to Thomson in 1881 [9].

I shall discuss his arguments in modern language. At the time, the electron was conceived as a classical particle, a small rigid sphere with radius a and charge q_e. Let it be at rest in the origin of the axes of the reference frame Σ₀. In this frame the magnetic field is zero and, outside the sphere, the electric field is the field of a point charge in the origin. The corresponding (electrostatic) energy, calculated integrating the electric field energy over the space, Eq. (6), is

$$U_{0}^{elst} = \frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi^{2} \varepsilon_{0} }}\frac{1}{a}$$

(30)

Thomson then considers the charged sphere moving with uniform velocity v (much smaller than c), say in the frame Σ. The electric field, and consequently the electric energy, are substantially the same as in Σ₀. However there is now also a magnetic field, which, with the usual expression Eq. (6), gives the additional contribution to energy

$$U^{magn} = \frac{1}{2}\left( {\frac{{q_{e}^{2} }}{{4\pi^{2} \varepsilon_{0} }}\frac{1}{{c^{2} a}}} \right)v^{2}$$

(31)

We see that the additional field energy, when the electron is in motion, is proportional to the square of its speed and the proportionality constant, the quantity in parenthesis, depends only on electron properties, its charge and its radius. We can conclude, with Thomson, that Eq. (31) gives the additional “kinetic energy due to electrification”. The effect of electrification, concludes Thomson, “is the same as if the mass of the sphere were increased by”

$$m^{EM} = \frac{1}{2}\left( {\frac{{q_{e}^{2} }}{{4\pi^{2} \varepsilon_{0} }}\frac{1}{{c^{2} a}}} \right)v^{2}$$

(32)

Thomson did not do the last step, which is however a logical consequence of his argument. Indeed, by comparing Eq. (32) with Eq. (30), we see that the following relation holds between “electromagnetic mass” and rest energy

$$m^{EM} c^{2} = \frac{4}{3}U_{0}^{elect}$$

(33)

The solution of the 4/3 problem was first given by a 21-year old student in 1922, Enrico Fermi.

As it is known, simple electrodynamic arguments lead to the value (4/3)U/c² for the electromagnetic mass of a spherical system containing the energy U… On the other hand it is well known that simple relativistic considerations lead to the value U/c² for the mass of a system containing the energy U. Consequently, we are confronted by a conflict between two different conceptions. It looks to me not to be without interest to clarify such a conflict, especially if one takes into account the enormous importance for physics of the concept of electromagnetic mass. [63]

He shows that the problem is basically due to the fact, as we have said, that Eqs. (6) are not Lorentz-invariant. However, the Fermi paper went largely unnoticed, and the problem remained in the community. It was solved again, independently and with different arguments, in 1936 by W. Wilson [64]. This paper was forgotten too and once more independently brought on again by B. Kwal [65] in 1949, to be forgotten in turn. Finally, once more without knowing the previous results, it was brought to the general attention by F. Rohrlich as late as in 1960 [43].

The same 4/3 factor appears if one tries to obtain the electromagnetic mass from the electromagnetic momentum defined by Eq. (6). Feynman in his famous Lectures on Physics [66] given in 1961–63 writes

$${\mathbf{P}} = \varepsilon_{0} \int_{{}} {{\mathbf{E}} \times {\mathbf{B}}\,dV = \left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right)\frac{4}{3}{\mathbf{v}}}$$

(34)

This electromagnetic momentum is proportional to the velocity and that the proportionality constant depends only on the charge and radius of the sphere. At low velocities the momentum is the mass times the velocity and we can identify this constant with the mass

$$m^{EM} c^{2} = \left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right)\frac{4}{3} = \frac{4}{3}U_{0}^{{{\text{elect}}}}$$

(35)

The reason of the problem is again the use the non-covariant expressions Eqs. (6). Surprisingly enough, this simple consideration escaped to Feynman himself! He correctly explains that the total energy momentum, namely is the sum of the electromagnetic and mechanical ones, must be considered. However he links the issue to the problem of the stability of the electron. Since the Poincaré times the two problems have been connected, making the issue artificially confused.

The “4/3 problem” disappears immediately if the covariant expressions of Eq. (27) are used. At v <  < c the first equation can be approximated with

$${\mathbf{P}} = \varepsilon_{0} \mathop \smallint \limits_{V}^{{}} \left[ {{\mathbf{E}} \times {\mathbf{B}} + \frac{1}{{c^{2} }}\left( {{\mathbf{v}} \cdot {\mathbf{E}}} \right){\mathbf{E}} - \frac{1}{{2c^{2} }} E^{2} {\mathbf{v}}} \right]{\mathbf{dV}}$$

(36)

The right hand side contains three terms, the one of Eq. (28) plus other two. They give

$${\mathbf{P}} = \frac{{\varepsilon_{0} }}{{c^{2} }}\mathop \smallint \limits_{V}^{{}} \left( {{\mathbf{v}} \cdot {\mathbf{E}}} \right){\mathbf{E }}dV = \left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right)\frac{2}{3}{\mathbf{v}}$$

and

$${\mathbf{P}} = - \frac{{\varepsilon_{0} }}{{2c^{2} }} {\mathbf{v}}\mathop \smallint \limits_{V}^{{}} E^{2} dV = - \left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right){\mathbf{v}}$$

Summing up

$${\mathbf{P}} = \left( {\frac{4}{3} + \frac{2}{3} - 1} \right)\left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right){\mathbf{v}} = \left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right){\mathbf{v}}$$

(37)

And

$$m^{EM} c^{2} = \left( {\frac{1}{2}\frac{{q_{e}^{2} }}{{4\pi \varepsilon_{0} c^{2} }}\frac{1}{a}} \right) = U_{0}^{elect}$$

(38)

8 Conclusions

Looking at history, we learn that the progress of physics, and science in general, is often far from being linear. The story I have told here starts with a very brilliant idea to test a wrong hypothesis. The null result of the following experiments falsified the hypothesis but verified a basic principle of physics. The impact of the result, however, from this point of view was marginal. On the other hand, attempts to explain what looked like a paradox showed intriguing aspects of energy and momentum conservation in classic electromagnetism. This process was not linear but converged to a better understanding of the interplay between electromagnetic field and matter.