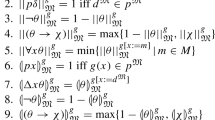On discernibility in symmetric languages: the case of quantum particles

Abstract

In this paper I consider the question of whether absolute discernibility is attainable in symmetric languages. Simon Saunders has proven that all facts expressible in first-order language with identity can be equivalently stated within its symmetric sublanguage. I use this result to show specifically how particles of the same type can be absolutely discerned in the permutation-invariant language of the quantum theory of many particles.

The main problem considered in this paper comes down to this simple question: is it possible to discern (in an appropriate sense of the word) objects in a language that is fully symmetric (meaning that the denotations of its formulae are permutation-invariant)? The motivation behind asking such a question derives from physics: as is well known, the quantum theory of many particles imposes a restriction on the available states of particles of the same type in the form of the requirement of their permutation invariance. As some claim, the permutation invariance of the states of composite systems leads directly to the consequence that the components of such systems can never be qualitatively discerned by their properties (in gross violation of the Leibnizian Principle of the Identity of Indiscernibles).¹ In what follows I will critically evaluate this claim, citing some general facts provable within first-order logic and applying them to the specific case of quantum particles. The conclusion I am aiming to argue for is that the symmetry of a language in which we describe quantum objects of the same type does not block the possibility of making absolute discernments between them.

The plan of the paper is as follows. In Sect. 1 I will present and briefly discuss three fundamental notions of discernibility (absolute, relative and weak) commonly used in the literature on the subject, together with the logical relations holding among them. Section 2 contains an extended analysis of the requirement of symmetry (permutation-invariance) as applied to languages. After recalling the standard logical result showing that the symmetry of a language implies the non-existence of absolutely and relatively discerning formulas, I lay out a theorem due to Simon Saunders which implies that symmetric first-order languages are capable of expressing facts about absolute (and relative) discernibility. I also explain why the two above-mentioned results, while seemingly contradictory, are in no conflict with one another. Sections 3 and 4 are devoted to the task of applying Saunders’ theorem to the case of the quantum theory of many particles. In Sect. 3 I take up the task of translating the basic elements of the quantum–mechanical formalism into a first-order language, which to my knowledge has never been done in a systematic way. I propose to introduce multi-variable predicates whose satisfaction by sequences of objects is explicated in terms of the state of the system being an eigenstate for a particular projection operator. In Sect. 4 I show directly how to use Saunders’ theorem in order to argue that the symmetric language describing states of groups of ‘indistinguishable’ fermions and bosons contains expressions which can be interpreted as stating that particles are absolutely discernible by appropriate properties. I point out that this result hinges on the assumption that the logical connectives are to be interpreted non-classically (quantum-logically), and I briefly discuss the consequences of this assumption.

1 Discernibility in a language

In the first step we should define what we mean by discernibility with respect to a given language. We will present here the standard approach to this problem, expressed in the most concise way in the overview (Ladyman et al. 2012).² Let ℒ be a first-order language without proper names (constants) and without the identity symbol, whose intended semantic interpretation is given in the form of a particular relational structure ${\mathcal{A}}$ (consisting of a non-empty set and a number of relations of various numbers of arguments corresponding to the primitive predicates of ℒ). We will distinguish three basic types of discernibility that can be expressed in ℒ under the semantic interpretation encompassed in the model ${\mathcal{A}}$. These types are known as absolute discernibility, relative discernibility and weak discernibility. Objects a and b in the domain of the model ${\mathcal{A}}$ are said to be absolutely discernible in ℒ iff there is a one-argument formula Φ(x) in ℒ such that Φ(x) is satisfied by a and not by b in ${\mathcal{A}}$.³ Objects a and b are relatively discernible in ℒ iff there is a two-argument formula Φ(x, y) in ℒ such that Φ(x, y) is satisfied in ${\mathcal{A}}$ by pair (a, b) and not by (b, a). And, thirdly, objects a and b are weakly discernible in ℒ iff there is a formula Φ(x, y) in ℒ such that Φ(x, y) is satisfied in ${\mathcal{A}}$ by pairs (a, b) and (b, a), and is not satisfied by pairs (a, a) and (b, b).⁴ These three definitions can be concisely given as follows⁵:

Definition 1.1

Let a and b be elements of the domain of structure ${\mathcal{A}}$. Then

• (a) a and b are absolutely discernible in ℒ iff there is an open formula Φ(x) in ℒ such that ${\mathcal{A}}$ ⊨ Φ(a) and ${\mathcal{A}}$ ⊨ ¬Φ(b),⁶

• (b) a and b are relatively discernible in ℒ iff there is an open formula Φ(x, y) in ℒ such that ${\mathcal{A}}$ ⊨ Φ(a, b) and ${\mathcal{A}}$ ⊨ ¬Φ(b, a),

• (c) a and b are weakly discernible in ℒ iff there is an open formula Φ(x, y) in ℒ such that ${\mathcal{A}}$ ⊨ Φ(a, b) and ${\mathcal{A}}$ ⊨ ¬Φ(a, a).

We can also define what it means for a particular formula in ℒ to discern two objects—absolutely, relatively or weakly.

Definition 1.2

Let a and b be elements of the domain of structure ${\mathcal{A}}$. Then

• (a) formula Φ(x) in ℒ absolutely discerns objects a and b iff ${\mathcal{A}}$ ⊨ Φ(a) and ${\mathcal{A}}$ ⊨ ¬Φ(b), or ${\mathcal{A}}$ ⊨ Φ(b) and ${\mathcal{A}}$ ⊨ ¬Φ(a),

• (b) formula Φ(x, y) in ℒ relatively discerns objects a and b iff ${\mathcal{A}}$ ⊨ Φ(a, b) and ${\mathcal{A}}$ ⊨ ¬Φ(b, a), or ${\mathcal{A}}$ ⊨ Φ(b, a) and ${\mathcal{A}}$ ⊨ ¬Φ(a, b),

• (c) formula Φ(x, y) in ℒ weakly discerns objects a and b iff ${\mathcal{A}}$ ⊨ Φ(a, b), ${\mathcal{A}}$ ⊨ Φ(b, a), ${\mathcal{A}}$ ⊨ ¬Φ(a, a) and ${\mathcal{A}}$ ⊨ ¬Φ(b, b).

The second disjunct in (a) is necessary in order to make sure that discernibility by a formula is a symmetric relation: if Φ discerns a from b, it would be rather absurd to deny that Φ discerns b from a. Also, we want to ensure that if Φ discerns two objects, so does its negation ¬Φ. Similarly, the second clause of the disjunction in (b) ensures that discernibility by a formula is symmetric (even though in this case the discerning relation is clearly asymmetric—beware of conflating the cognate notions of being relatively discerned by a formula and being connected by a relation that does the discerning). In case (c) it is unnecessary to add the second clause, since the relation of weak discernibility is already stipulated to be symmetric.

Instead of considering the purely ‘qualitative’ language ℒ, we could expand it to ℒ^* by adding either a proper name for every element in the domain (given the assumption that the intended model ${\mathcal{A}}$ is finite), or by adding the symbol of identity = with its intended interpretation {(a₁, a₁), (a₂, a₂), … (a_n, a_n)} to ℒ⁼. That way we will obtain new languages ℒ^* and ℒ⁼ and new corresponding notions of discernibility. All in all, we have introduced nine distinct grades of discernibility, which turn out to be mutually connected by relations of logical entailment. These relations can be synthetically presented in the following theorem (the abbreviations used in the theorem should be self-explanatory)⁷:

Theorem 1.1

The following logical relations hold:

• (a) Abs_ℒ ⇒ Rel_ℒ ⇒ Weak_ℒ

• (b) Abs_ℒ ⇒ Abs_ℒ=

• (c) Rel_ℒ ⇒ Rel_ℒ=

• (d) Abs_ℒ= ⇒ Rel_ℒ= ⇒ Weak_ℒ

• (e) Weak_ℒ ⇔ Weak_ℒ* ⇔ Abs_ℒ* ⇔ Rel_ℒ*

• (f) Weak_ℒ= ⇔ ≠

• (g) No implications other than those entailed by (a)–(f) hold true.

Of particular importance to us are clauses (a) and (d) which show (together with (e) and (g)) that weak discernibility is indeed the weakest of all typical grades of discernibility, with absolute discernibility in ℒ the strongest of all. Clause (e) shows that in a language equipped with proper names for every element of the domain all grades of discernibility collapse into weak discernibility. Clause (f) establishes that weak discernibility in a language with identity is trivially non-identity.

2 Discernibility and symmetry

It is common knowledge that the language in which we are supposed to describe systems of quantum particles of the same type should satisfy the requirement of symmetry, also known as permutation invariance. Of course, the primary reason for the symmetry of a language is that the corresponding reality described by the language is supposed to be symmetric too. Thus, in the case of the language of quantum mechanics its symmetry follows from the fact that the physical states of particles of the same type described in this language are supposed to be permutation-invariant. Due to the correspondence between language ℒ and its intended interpretation ${\mathcal{A}}$, we can move back and forth between the symmetry of the language and the symmetry of its corresponding model. But what does it precisely mean for a language to be permutation invariant (symmetric)? The standard definition can be given as follows.

Definition 2.1

Let ℒ be a first-order language and ${\mathcal{A}}$ its intended interpretation. Let σ: Dom(${\mathcal{A}}$) → Dom(${\mathcal{A}}$) be a permutation of the domain of ${\mathcal{A}}$ (that is, a bijection of Dom(${\mathcal{A}}$) onto itself). Then ℒ is symmetric iff for every open formula Φ(x₁, x₂, … x_n) in ℒ and any permutation σ, ${\mathcal{A}}$ ⊨ Φ(a₁, a₂, … a_n) iff ${\mathcal{A}}$ ⊨ Φ(σ(a₁), σ(a₂), … σ(a_n)).⁸

It can be proven relatively easily (by induction over the complexity of formulas) that Definition 2.1 is equivalent to the condition of symmetry imposed on the structure ${\mathcal{A}}$ corresponding to ℒ, spelled out as follows:

Definition 2.2

Relational structure ${\mathcal{A}}$ is symmetric iff for any k-element relation R in ${\mathcal{A}}$, any elements a₁, …, a_k ∈ Dom(${\mathcal{A}}$) and any permutation σ: Dom(${\mathcal{A}}$) → Dom(${\mathcal{A}}$), Ra₁…a_k iff Rσ(a₁)…σ(a_k).

The following fact regarding discernibility in symmetric languages holds:

Theorem 2.1

Let ℒ be a symmetric language (in the sense of Definition 2.1 ). Then no two objects in Dom( ${\mathcal{A}}$ ) are absolutely or relatively discerned in ℒ.

The proof of this theorem is quick. Suppose that elements a and b of the domain Dom(${\mathcal{A}}$) are relatively discerned in ℒ. That means, according to Definition 1.1. (b) that there is a formula Φ(x, y) in ℒ such that ${\mathcal{A}}$ ⊨ Φ(a, b) and ${\mathcal{A}}$ ⊨ ¬Φ(b, a), but this directly contradicts Definition 2.1, since the transposition σ(a) = b and σ(b) = a does not preserve the satisfaction of formula Φ(x, y). Thus a and b can’t be relatively discerned in ℒ. And because of Theorem 1.1 (a), this implies that a and b are not absolutely discernible either. Theorem 2.1 remains also valid for languages with identity ℒ⁼ when we limit ourselves to finite models, but its proof is more complicated (see Caulton and Butterfield 2012, Sect. 4.3).

On the other hand, the symmetry of ℒ does not exclude the possibility of weak discernment, as seen in the following example. In the two-element symmetric graph given in Fig. 1, the double arrow represents a relation corresponding to a primitive, two-place predicate P in ℒ (note that the relation used in the graph is irreflexive, as no object is connected to itself by an arrow). Clearly, the graph is invariant under the permutation of objects, and yet they are weakly discernible by formula P(x, y).⁹

Fig. 1

A two-element symmetric graph

One lesson from this basic logical analysis seems to be inescapable: if we have at our disposal a symmetric language only, we can at best achieve weak discernibility but not relative and not absolute discernibility. This conclusion apparently supports the orthodox approach to the question of the discernibility of quantum particles of the same type. It is commonly accepted that in the permutation-invariant language of the quantum theory of many particles no absolute discernibility is possible, but weak discernibility is sometimes attainable.¹⁰ However, in what follows we will try to cast doubt on the inevitability of this conclusion. We will start with a relatively little-known theorem due to Saunders (2006b, 2013), which, on the face of it, seems to contravene the conclusion that symmetry prevents absolute discernment.

Theorem 2.2

Let ℒ⁼ be a first-order language without proper names but with the identity symbol. Then for every sentence T in ℒ⁼ and every natural number N, there is a sentence S in ℒ⁼ of the form S = ∃x₁…∃x_n G(x₁, …, x_n) such that predicate G is symmetric, and S is equivalent to T in all models of cardinality N.

The sketch of a proof for this theorem is as follows (for details see Saunders 2006b, pp. 209–210). Every sentence T can be presented in the standard prenex form as Q₁, …, Q_n F(x₁, …, x_n), where Q_i is either ∃x_i or ∀x_i. In order to construct the corresponding symmetric sentence S, we eliminate every quantifier Q_i step by step, starting with Q_n, while simultaneously replacing formula F(x₁, …, x_n) with either a conjunction (when Q_i is the universal quantifier) or a disjunction (when Q_i is the existential quantifier) of formulas F(…a₁…), …, F(…a_N…), where all occurrences of the variable x_i are replaced with unique names a₁, …, a_N of all elements in the domain. For instance, the first step in the procedure in the case when Q_n is universal will give us formula

$$ Q_{1} \ldots Q_{n - 1} [F\left( {x_{1} , \ldots ,x_{n - 1} ,a_{1} } \right) \wedge F\left( {x_{1} , \, \ldots ,x_{n - 1} ,a_{2} } \right) \wedge \ldots \wedge F\left( {x_{1} , \, \ldots ,x_{n - 1} ,a_{N} } \right)]. $$

After finishing this procedure, we end up with a formula with no quantifiers but instead containing constants a₁, …, a_N. Finally, we replace every occurrence of a_i with a variable x_i bound by an existential quantifier, and we add to the entire sentence the formula stating that all x_i’s are distinct and that they exhaust the entire domain (every object in the domain is identical with some x_i). The sentence S obtained during this procedure is symmetric by design, and it is also not difficult to observe that it must be equivalent to T in all models of cardinality N.

Theorem 2.2 seems to be highly relevant to the issue of the relation between symmetry and discernibility. Suppose that ℒ⁼ is a language in which all elements of a (finite) domain Dom(${\mathcal{A}}$) are absolutely discernible. Then, Theorem 2.2 ensures that all true sentences about this domain expressible in ℒ⁼ can be equivalently formulated in its symmetric sublanguage Sym(ℒ⁼) consisting of permutation-invariant formulas only. And since the collection of all sentences of ℒ⁼ true in ${\mathcal{A}}$ presumably include truths regarding absolute discernibility of objects in Dom(${\mathcal{A}}$), it follows that these truths are expressible in the symmetric language Sym(ℒ⁼). However, we have to be careful here. The way we defined absolute discernibility in Definition 1.1 (a) does not automatically ensure that facts regarding the absolute discernibility of objects will be expressible in language ℒ⁼, since the definition is given in the metalanguage. And, as we learn from the well-known limitation theorems about the non-definability of truth or consistency, not all metalinguistic facts about a given language (or a theory formulated in that language) can be expressed in the language (theory) itself. In particular, even though objects a and b are absolutely discernible by formula Φ(x) in ℒ⁼, this very truth may not be expressible in ℒ due to the simple fact that ℒ does not contain proper names for a and b.

Approaching this problem more generally, we may ask whether there is a sentence Abs in ℒ⁼ which states that all objects in the finite domain of ℒ are absolutely discernible from each other. And it is easy to see that the answer to this question is “yes”. Let the elements of the domain be symbolized as {a₁, …, a_N}. By assumption, for every pair (a_i, a_j) such that i ≠ j there is a formula Φ_ij(x) in ℒ⁼ that absolutely discerns a_i and a_j, that is ${\mathcal{A}}$ ⊨ [Φ_ij(a_i) ∧ ¬Φ_ij(a_j)] ∨ [Φ_ij(a_j) ∧ ¬Φ_ij(a_i)]. If we take the disjunction of all such formulas over all possible i ≠ j, it is clear that the resulting formula must be satisfied by every pair of distinct objects, and that the satisfaction of the universal generalization of this formula is equivalent to the statement that all distinct objects are absolutely discernible. Hence, the sought-after sentence is as follows:

• (1) $Abs \equiv \forall x\forall y\left\{ {x \ne y \to {\bigvee }_{i \ne j}^{N} \left[ {\varPhi_{ij} \left( x \right) \wedge \neg \varPhi_{ij} \left( y \right)} \right] \vee \left[ {\varPhi_{ij} \left( y \right) \wedge \neg \varPhi_{ij} \left( x \right)} \right]} \right\}$.¹¹

Now we can apply Saunders’ procedure from Theorem 2.2 to the rhs of formula (1), eliminating every universal quantifier and adding an N-argument conjunction of formulas with constants to obtain the following:

• (2) ${\bigwedge }_{k,l = 1}^{N} \{ a_{k} \ne a_{l} \to {\bigvee }_{i \ne j}^{N} [\varPhi_{ij} \left( {a_{k} } \right) \wedge \neg \varPhi _{ij} \left( {a_{l} } \right)] \vee [\varPhi_{ij} \left( {a_{l} } \right) \wedge \neg \varPhi _{ij} \left( {a_{k} } \right)]\}$

Finally, we will obtain the totally symmetric formula logically equivalent (in N-element domains) to the original statement Abs:

• (3) $\exists x_{1} \ldots \exists x_{N} \Big\{ \rho \Big( x_{1} , \ldots ,x_{N} \Big) \wedge {\bigwedge }_{k \ne l}^{N} \Big\{ x_{k} \ne x_{l} \to {\bigvee }_{i \ne j}^{N} [\varPhi_{ij} \Big( {x_{k} } \Big) \wedge \neg \varPhi_{ij} \Big( {x_{l} } \Big)] \vee [\varPhi_{ij} \Big( {x_{l} } \Big) \wedge \neg \varPhi _{ij} \Big( {x_{k} } \Big)] \Big\} \Big\}$

where $\rho \left( {x_{1} , \ldots ,x_{N} } \right)$ abbreviates the following: ${\bigwedge }_{i \ne j}^{N} x_{i} \ne x_{j} \wedge \forall x {\bigvee }_{k = 1}^{N} x = x_{k}$, that is the formula stating that there are exactly N objects in the domain.¹²

A similar result obtains in the case of relative discernibility. That is, if all objects are relatively discernible in language ℒ⁼, then the following sentence expresses this very fact in finite domains of cardinality N (formula Ψ_ij(x, y) is assumed to relatively discern objects a_i and a_j):

• (4) $Rel \equiv \forall x\forall y\left\{ {x \ne y \to {\bigvee }_{i \ne j}^{N} [\psi_{ij} \left( {x,y} \right) \vee \psi _{ij} \left( {y,x} \right)]} \right\}$

The rhs of the equivalence (4) after symmetrization will look similar to (3):

• (5) $x_{1} \ldots \exists x_{N} \left\{ {\rho \left( {x_{1} , \ldots ,x_{N} } \right) \wedge {\bigwedge }_{k \ne l}^{N} \{ x_{k} \ne x_{l} \to {\bigvee }_{i \ne j}^{N} [\psi_{ij} \left( {x_{k} ,x_{l} } \right) \wedge \psi _{ij} \left( {x_{l} ,x_{k} } \right)] } \right\}$

Now we are in a position to explain away the apparent inconsistency between Theorems 2.1 and 2.2. The impossibility of absolute (and relative) discernibility in symmetric languages, as stated in Theorem 2.1, means that there is no symmetric formula that would discern objects absolutely or relatively. Nevertheless, this does not preclude the possibility that there may be a symmetric sentence expressing the fact that objects are absolutely (or relatively) discernible in a broader, non-symmetric language. Sentences (1) and (2) are constructed with the help of symmetric combinations of predicates from a non-symmetric language ℒ⁼, but they don’t assert the possibility of absolute (relative) discernibility in Sym(ℒ⁼), but in ℒ⁼. The possibility of conveying in a symmetric language the fact that some objects are absolutely discernible in a different, non-symmetric language, does not invalidate the fact, stated in Theorem 2.1, that absolute discernment, as defined in Definition 1.1, cannot be literally achieved in a symmetric language. However, if sentences (3) or (5) are true, we are justified in claiming that objects in the domain are in fact discernible by appropriate properties or relations, even though these properties and relations cannot find their direct linguistic representations in Sym(ℒ⁼).¹³ The issue of the appropriateness of these properties and relations in the case of the quantum theory of many particles will be discussed in the next section.

3 Quantum–mechanical predicates

The next logical step should be to apply the general analysis done above to the specific case of systems of many particles obeying symmetry restrictions. The idea is of course to see whether absolute discernibility can be proven to be satisfied in the case of particles occupying permutation-invariant states, following the method from Theorem 2.2. However, when attempting to do this, we immediately encounter a serious stumbling block. The problem is that there is no straightforward way to cast the quantum–mechanical formalism in terms of first-order logic with its well-known structure of multi-variable predicates and logical constants. So far no rigorous and systematic method of translating the quantum–mechanical framework into standard first-order logic has been proposed, apart from some rather limited in scope and ad hoc translations used for specific purposes.¹⁴ In what follows we will try to approach this problem more generally, but the result will be partially negative in that it will be shown that certain translations cannot be done for some rather fundamental reasons. However, what can be done should be sufficient for the purpose of answering the main question of this article.

Before we move on to the specific task of constructing a first-order language for the quantum theory of many particles (QTMP), one general remark is in order. As we have seen, Saunders’ Theorem 2.2 assumes that the considered language does not contain proper names (individual constants). This may be seen as contradicting the standard practice of QTMP, which commonly uses indices (labels) as names of individual particles. In particular, the requirement of permutation invariance is typically cast in a language that uses labels as individual constants. However, as we will see below, the presence of individual constants is by no means necessary to express the requirement of permutation invariance in quantum mechanics. The permutation invariance of a particular formula can be expressed in the metalanguage, as in Definition 2.1, where only metalinguistic terms are used. Thus there is no reason to believe that Saunders’ theorem is inapplicable to the case of the language of QTMP.¹⁵

We will start with the simplest case of one quantum–mechanical system with no proper parts. The standard way to formally represent a specific property¹⁶ of this system is with the help of a particular subspace of the entire Hilbert space of states for this system or, equivalently, of a projector onto that subspace (there is a one-to-one correspondence between orthogonal projectors and subspaces onto which they project). That is, the fact that a given physical system possesses a particular property is formally expressed by saying that its state vector |v〉 lies in a given subspace ${\mathcal{V}}$ of ℋ (or, alternatively, that |v〉 is an eigenstate of the corresponding projector $P_{{\mathcal{V}}}$ with the eigenvalue 1).¹⁷ In the case when ${\mathcal{V}}$ is one-dimensional (a ray) we say that the property is categorical (it amounts to the fact that there is a maximal, non-degenerate observable O whose value is determined when vector |v〉 lies in ${\mathcal{V}}$). But ${\mathcal{V}}$ may be more than one-dimensional, in which case the property is less specific, given the assumption that O is non-degenerate (in such a case it is usually assumed that the value of a particular observable O lies within a certain range of possible values rather than being determined sharply).

Given that we are considering the domain containing one object only, we can safely limit ourselves to monadic predicates in our first-order language reconstruction. And there is a natural and simple correspondence between properties represented by projectors and one-argument predicates satisfiable by the considered system. Let $\Phi_{{P_{{\mathcal{V}}} }} (\xi )$ be a monadic predicate in the language that we are constructing such that

• (6) $\Phi_{{P_{{\mathcal{V}}} }} (\xi )$ is satisfied by the system a iff a is in a state |v〉 such that $P_{{\mathcal{V}}}$|v〉 = |v〉.¹⁸

In other words, $\Phi_{{P_{{\mathcal{V}}} }} \left( a \right)$ is true, if the vector representing the state of system a lies in subspace ${\mathcal{V}}$ (we are presupposing the eigenstate-eigenvalue link here). If we assume that for each projector there is a corresponding predicate, we can express in our language any simple sentence regarding the possession of quantum–mechanical properties by the system. One small problem with this assumption is that we may have to accept the existence of an infinite (in fact uncountably infinite) number of primitive predicates. Alternatively, we may introduce one two-place predicate Φ(ξ, ${\mathcal{V}}$) whose truth conditions are exactly as stated in the rhs of the equivalence in (6). Finally, if one wishes, one can use a three-place predicate Φ(ξ, ${\mathcal{V}}$, φ) which is satisfied by an object a, a subspace ${\mathcal{V}}$ and a state |φ〉 iff |φ〉 is the state of a and |φ〉 ∈ ${\mathcal{V}}$.

Now we will have to extend our language to describe systems of many particles. Suppose, then, that we have N particles jointly forming a system described by a state vector |φ(1, …, N)〉. Our goal will be to define predicates with arity k smaller or equal N. The idea, again, is that these predicates should correspond to appropriate projectors acting in the tensor product ℋ^N = ℋ₁ ⊗ … ⊗ ℋ_N. However, we have to proceed cautiously, since concrete projectors are already ‘attached’ to specific factor Hilbert spaces, and predicates in formalized language should be satisfiable by various combinations of objects. Thus we cannot tie a given k-argument predicate to a particular projector, but rather to an entire class of projectors that share their ‘physical’ meaning while being attributed to different objects in the composite system. This can be done as follows. Let us start with a particular subset of the set of N objects which can be picked using simply numbers as labels: 1, …, k (keep in mind that these are labels that belong to the metalanguage, not the first-order language that we are constructing). A specific property of this subset can be represented by any projector that is the product of k projectors acting in the first k Hilbert spaces, and N − k identity operators acting in the remaining spaces: $P_{1}^{{(a_{1} )}} \otimes \ldots \otimes P_{k}^{{\left( {a_{k} } \right)}} \otimes I_{k + 1} \otimes \ldots \otimes I_{N}$. In addition to that, some linear combinations of projectors of this type can also be permitted, even though not all such combinations will produce projectors, which are idempotent operators.¹⁹ Generally, all permissible operators representing properties of the first k particles can be written in the following form:

• (7) Ω_k = P(1, …, k) ⊗ I(k + 1, …, N),

where P(1, …, k) is any projector acting in the k-fold tensor product of Hilbert spaces ℋ₁ ⊗ … ⊗ ℋ_k, and I(k + 1, …, N) is the product of N − k identity operators.

The k-argument predicate $\Phi_{{\varOmega_{k} }}$ corresponding to the above projector Ω_k has to be built step by step. In the first step we specify the truth condition for $\Phi_{{\varOmega_{k} }}$ applied to particles 1, …, k as follows:

• (8) $\Phi_{{\varOmega_{k} }} \left( {\xi_{1} , \ldots ,\xi_{k} } \right)$ is satisfied by the k-tuple (1, …, k) iff the N-element system is in a state |φ〉 such that Ω_k|φ〉 = |φ〉.²⁰

In order to stipulate the condition of the satisfaction of $\Phi_{{\varOmega_{k} }}$ for any other k-tuple, we have to transform the projector Ω_k accordingly. That is, let σ be any permutation of the set of metalinguistic labels {1, …, N}. In that case we stipulate the following to be true:

• (9) $\Phi_{{\varOmega_{k} }} \left( {\xi_{1} , \ldots ,\xi_{k} } \right)$ is satisfied by the k-tuple (σ(1), …, σ(k)) iff the N-element system is in a state |φ〉 such that σ⁻¹Ω_k σ|φ〉 = |φ〉.

As can be seen from the above, the satisfaction of the predicate $\Phi_{{\varOmega_{k} }}$ by any sequence of objects other than 1, …, k requires that we transform the operator Ω_k to be applicable to this sequence. That way we can cover all cases of satisfaction of predicate $\Phi_{{\varOmega_{k} }}$ by k-element sequences formed from the set {1, …, N} with no repetitions. However, there remains cases in which $\Phi_{{\varOmega_{k} }}$ is applied to sequences with repetitions. And these cases present us with a difficulty that ultimately cannot be overcome in full generality, except in some special cases. Let us explain what we are up against here using the simplest possible case of two particles (N = 2). Let Ω⁽²⁾ be any projector acting in the product ℋ₁ ⊗ ℋ₂. The corresponding two-argument predicate $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ will receive the following partial characteristics:

• (10) $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ is satisfied by pair (1, 2) iff the system is in a state |φ(1,2)〉 such that Ω⁽²⁾|φ(1,2)〉 = |φ(1,2)〉;

  $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ is satisfied by pair (2, 1) iff the system is in a state |φ(1,2)〉 such that P₁₂Ω⁽²⁾P₁₂|φ(1,2)〉 = |φ(1,2)〉, and therefore Ω⁽²⁾|φ(2,1)〉 = |φ(2,1)〉.

However, in addition we have to stipulate the conditions for satisfaction of predicate $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ by pairs (1, 1) and (2, 2), and this turns out to be a harder nut to crack. We can suggest the following solution to this problem in the special case when Ω⁽²⁾ = P_a ⊗ P_b, and P_a commutes with P_b:

• (11) $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ is satisfied by pair (1, 1) iff the system is in a state |φ(1,2)〉 such that P_aP_b ⊗ I|φ(1,2)〉 = |φ(1,2)〉,

  $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ is satisfied by pair (2, 2) iff the system is in a state |φ(1,2)〉 such that I ⊗ P_aP_b|φ(1,2)〉 = |φ(1,2)〉.²¹

What justifies the correctness of these stipulation is that in this special case the property represented by projector P_aP_b is just the ordinary conjunction of one-particle properties represented by P_a and P_b. Thus the satisfaction of predicate $\Phi_{{\varOmega^{\left( 2 \right)} }} \left( {\xi_{1} ,\xi_{2} } \right)$ by pair (1, 1) (or (2, 2)) means simply that object 1 (or 2) possesses both attributes P_a and P_b, and this is precisely what the above conditions guarantee. However, this characteristic is formally incorrect when P_a and P_b do not commute, since in that case P_aP_b is not a projector. Moreover, the proposed method of interpretation cannot be applied to more complex cases, such as for instance when the operator Ω⁽²⁾ is equal to P_a ⊗ P_b + P_b ⊗ P_a (where P_a and P_b are orthogonal) In that case it simply does not make much sense to ask what the property represented by this symmetric projector would look like when applied ‘twice over’ to one particle. Speaking figuratively, the ‘entanglement’ of the property of a two-particle system represented by P_a ⊗ P_b + P_b ⊗ P_a makes it impossible to disentangle it in a way necessary to turn it into a relational property of one particle.

In conclusion, it is possible to define many-argument quantum predicates applicable to sequences of distinct objects; however ‘contractions’ of such predicates with smaller numbers of arguments are well defined only in special cases.

4 Absolute discernibility in the quantum theory of many particles

In this section we will make use of the tools developed in the previous sections in order to formally argue that absolute discernibility is attainable in the quantum–mechanical formalism of many-particle systems, even if these systems can only occupy permutation-invariant states. Let us consider the most general case of N particles, labeled by natural numbers 1, …, N, and let us suppose that they have been prepared in the product state

$$ |\left. {\chi \left( {1, \, \ldots N} \right)} \right\rangle = \left| {a_{1} } \right\rangle \left| {a_{2} } \right\rangle \ldots \left| {a_{N} } \right\rangle , $$

where each two vectors |a_i〉 and |a_j〉 are orthogonal for i ≠ j.²² Moreover, let P⁽ⁱ⁾ = |a_i〉〈a_i|. Now we can define N monadic predicates Φ_i(ξ), where i = 1, …, N, as follows:

• (12) Φ_i(ξ) is satisfied by particle j iff the system is in a state |φ〉 such that $\varOmega_{j}^{\left( i \right)} \left| \varphi \right\rangle = \left| \varphi \right\rangle$, where $\varOmega_{j}^{\left( i \right)} = I \otimes I \ldots \otimes \underbrace {{P^{\left( i \right)} }}_{j} \otimes \ldots \otimes I$.

It is elementary to observe that if the system is in state |χ(1, … N)〉 defined above, then for every i, the ith particle satisfies predicate Φ_i(x) and only it. Thus, for every k, l, ${\mathcal{A}}$ ⊨ Φ_k(k) ∧ Φ_l(l), from which it follows that for every k ≠ l, ${\mathcal{A}}$ ⊨ Φ_k(k) ∧ ¬Φ_k(l). Consequently, each formula Φ_i(x) absolutely discerns the ith particle from every other particle. We can express this fact in the following general statement:

• (13) $\forall \xi_{1} \forall \xi_{2} \left\{ {\xi_{1} \ne \xi_{2} \to {\bigvee }_{k = 1}^{N} \left[ {\Phi_{k} \left( {\xi_{1} } \right) \wedge \neg \Phi _{k} \left( {\xi_{2} } \right)} \right]} \right\}$

Applying the method of symmetrization described in Sect. 2, we can reformulate the above ‘discernibility’ sentence in a permutation-invariant way:

• (14) $\exists \xi_{1} \ldots \exists \xi_{N} \left\{ {\rho \left( {\xi_{1} , \ldots ,\xi_{N} } \right) \wedge {\bigwedge }_{i \ne j}^{N} {\bigvee }_{k = 1}^{N} \left[ {\Phi_{k} \left( {\xi_{i} } \right) \wedge \neg \Phi_{k} \left( {\xi_{j} } \right)} \right]} \right\}$,

where $\rho \left( {\xi_{1} , \ldots ,\xi_{N} } \right)$, as before, states that there are exactly N distinct objects. Sentence (14) is built with the help of the totally symmetric N-argument predicate:

• (15) ${\text{Abs}}\left( {\xi_{1} , \ldots ,\xi_{N} } \right) \equiv {\bigwedge }_{i \ne j}^{N} {\bigvee }_{k = 1}^{N} \left[ {\Phi_{k} \left( {\xi_{i} } \right) \wedge \neg \Phi_{k} \left( {\xi_{j} } \right)} \right]$.

Now the question is whether Abs(ξ₁, …, ξ_N) can be constructed independently of definition (15), which is given in terms of non-symmetric predicates Φ_i(ξ). The reason for asking this question is that in languages obeying the condition of permutation-invariance, predicates Φ_i(ξ) are not admissible, so we can hardly use them to define other formulas, even if these formulas themselves turn out to be permutation-invariant. Following the method of interpreting quantum–mechanical predicates laid out in Sect. 3, we will try to find a symmetric projector with the help of which we could formulate truth conditions for predicate Abs(ξ₁, …, ξ_N) independently of (15). We will do this in steps, starting first with formulas Φ_k(ξ₁) ∧ ¬Φ_k(ξ₂). The truth conditions for such compound formulas can be given as follows:

• (16) Φ_k(ξ₁) ∧ ¬Φ_k(ξ₂) is satisfied by pair (i, j) iff the system is in a state |φ〉 such that $\varOmega_{ij}^{\left( k \right)} \left| \varphi \right\rangle = \left| \varphi \right\rangle$, where $\varOmega_{ij}^{\left( k \right)} = I \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{I - P^{\left( k \right)} }}_{j} \otimes \ldots \otimes I$.²³

Observe that we are interpreting the negation of the monadic predicate Φ_k(ξ) with the help of the projector I − P^(k), which is the orthogonal complement of P^(k). This is standard practice in so-called quantum logic; however, it stands in conflict with the ordinary, classical interpretation of negation.²⁴ Classically, when the negation ¬Φ_k(ξ) is true of a, this means that a occupies any state not in the range of P^(k). But the quantum-logical interpretation of negation is stronger—it requires that the state occupied by a be orthogonal to the space projected onto by P^(k). Quantum logic does not obey the metalogical principle of the excluded middle: the system a may be in a state in which neither Φ_k(ξ) nor its negation is true of a. In the current context we may observe that if we followed the classical interpretation of negation, then the formula ¬Φ_k(ξ) would not have an interpretation in terms of any projector, since the set of all vectors in a Hilbert space minus one ray is not a vector space, and cannot form the range of any projector.

Next, we will extend our projector-based interpretation to the disjunctive formula ${\bigvee }_{k = 1}^{N} [\Phi_{k} \left( {\xi_{1} } \right) \wedge \neg \Phi_{k} \left( {\xi_{2} } \right)]$:

• (17) ${\bigvee }_{k = 1}^{N} [\Phi_{k} \left( {\xi_{1} } \right) \wedge \neg \Phi_{k} \left( {\xi_{2} } \right)]$ is satisfied by pair (i, j) iff the system is in a state |φ〉 such that $\varGamma_{ij} \left| \varphi \right\rangle = \left| \varphi \right\rangle$, where $\varGamma_{ij} = \sum\nolimits_{k = 1}^{N} {\varOmega_{ij}^{\left( k \right)} }$.²⁵

This time we have adopted yet another quantum modification of a classical logical concept, namely that of disjunction. Quantum disjunction is interpreted in terms of the span of vector spaces in the following sense: if sentence α is true if and only if the state vector of the system lies in space ${\mathcal{V}}$_α, and the truth condition for sentence β is the same as above with space ${\mathcal{V}}$_β replacing ${\mathcal{V}}$_α, then the quantum disjunction α ∨ β is true iff the state vector lies in the space that is spanned by ${\mathcal{V}}$_α and ${\mathcal{V}}$_β. This interpretation of disjunction is weaker than classical disjunction based on the notion of set-theoretic sum rather than span. That is, if the state of the system is given as a non-trivial linear combination of states from ${\mathcal{V}}$_α and ${\mathcal{V}}$_β, the quantum disjunction of sentences α and β is true but the classical disjunction is false.

Finally, we can present the complete projector corresponding to the symmetric predicate Abs defined in (15):

• (18) Abs(ξ₁, …, ξ_N) is satisfied by an N-tuple (a₁, …, a_N), where a_i ≠ a_j for i ≠ j, iff the system is in a state |φ〉 such that Ξ|φ〉 = |φ〉, where $\varXi = \prod\nolimits_{i \ne j}^{N} {\varGamma_{ij} } = \prod\nolimits_{i \ne j}^{N} {\sum\nolimits_{k = 1}^{N} {\varOmega_{ij}^{\left( k \right)} } }$.²⁶

Note that this time the appropriate projector Ξ does not depend on the selected sequence of objects (a₁, …, a_N), thanks to the permutation invariance of the corresponding predicate. Also, we may observe that the interpretation of the logical connective of conjunction in terms of the product of (commuting) projectors that underlies definition (18) is equivalent to that adopted in classical logic. The formal reason for this is that the intersection (set-theoretical product) of two vector spaces is itself a vector space.

It can be verified that projector Ξ has the following, simple form (see “Appendix”):

• (19) $\varXi = \mathop \sum \limits_{\sigma } P^{\sigma \left( 1 \right)} \otimes P^{\sigma \left( 2 \right)} \otimes \ldots \otimes P^{\sigma \left( N \right)}$

Suppose, now, that the system of N ‘indistinguishable’ particles occupies one of the two following states, depending on whether we are dealing with bosons or fermions:

• (20) $\begin{aligned} {\text{Sym}}\left( {\left. {|\chi (1, \ldots ,N} \right\rangle } \right) & = \mathop \sum \limits_{\sigma } \left| {a_{\sigma \left( 1 \right)} } \right\rangle \left| {a_{\sigma \left( 2 \right)} } \right\rangle \ldots \left| {a_{\sigma \left( N \right)} } \right\rangle \\ {\text{Anti}}\left( {\left. {|\chi (1, \ldots ,N} \right\rangle } \right) & { = }\mathop \sum \limits_{\sigma } {\text{sgn}}(\sigma )\left| {a_{\sigma \left( 1 \right)} } \right\rangle \left| {a_{\sigma \left( 2 \right)} } \right\rangle \ldots \left| {a_{\sigma \left( N \right)} } \right\rangle \\ \end{aligned}$

It is straightforward to observe that vectors (20) lie in the range of the operator Ξ, as presented in (19). Thus, we can conclude that particles occupying states (20) are absolutely distinguishable by their properties.

5 Conclusion

Saunders’ theorem goes against the widely-held belief that permutation-invariance and absolute discernibility are irreconcilable. It shows that even in a language that consists of totally symmetric predicates it is possible to express facts about absolute discernibility of objects. And yet the application of this theorem to the case of quantum particles of the same type is not at all straightforward. The main challenge is to make sure that the totally symmetric predicate which encodes the statement about the absolute discernibility of objects can be expressed within the standard quantum–mechanical formalism that we use to describe systems of many particles. In order to accomplish that, I have proposed a particular way of introducing multi-argument predicates into the language of quantum theory. I have suggested that the satisfaction of a given predicate by a k-tuple of objects should be tied to the fact that the state of the system containing these objects lies in the range of a selected projection operator. Given this interpretational rule, I have shown that the symmetric formula encoding the sentence that all objects in the domain are absolutely discernible by one-particle projectors, corresponds to a particular permutation-invariant combination of these projectors. This correspondence ensures that when the system occupies a state represented by a vector within the range of this compound projector, it may be claimed that the individual particles are absolutely discerned by their quantum–mechanical properties.

It has to be stressed that the above result relies on one crucial assumption—namely that the logical connectives used in the symmetric formulation of the condition of absolute discernibility (3) are interpreted quantum-logically rather than classically. It may be argued that this assumption weakens slightly the absolute discernibility claim made at the end of Sect. 4, since this claim cannot be upheld if we decide to use the standard, classical interpretation. Moreover, one can raise the concern that the interpretation of sentence Abs in (1) and its symmetric reformulation (3) following Saunders’ method, as expressing the absolute discernibility of objects, implicitly presupposes the classical concepts of disjunction and negation. It is unclear whether we can continue to interpret Abs in the same way when we replace classical connectives with their quantum counterparts. In the end this may indicate that the problem of the absolute discernibility of quantum particles is more intricate than we have presented it in this survey. There are some independent arguments showing that the absolute discernibility of fermions in all states and of bosons in the majority of states is admissible, but these arguments presuppose a substantial change in the adopted interpretation of the quantum–mechanical formalism. In particular, we would have to abandon the doctrine of factorism, i.e. the claim that the factor Hilbert spaces in the symmetric and antisymmetric sections of the N-fold tensor product represent states of individual particles. Consequently, the symmetry properties of the states of many particles would no longer be connected with invariance with respect to permutations of particles, but would be treated analogously to gauge symmetries as reflecting the representational redundancy of the mathematical formalism.²⁷ Whether we follow this new approach, or continue to use the method based on Saunders’ theorem, one thing seems to be certain: the absolute discernibility of same-type quantum particles by their momentary properties is not a far-fetched concept after all.

Appendix

In what follows I will give a semi-formal argument aiming to show that any product vector of the form |a_σ(1)〉|a_σ(2)〉 … |a_σ(N)〉 is an eigenstate of the projector Ξ defined in (18), with corresponding eigenvalue equal 1, and consequently that the symmetric/antisymmetric combination of such vectors has the same property too. Let us begin with a reformulation of operators $\varOmega_{ij}^{\left( k \right)}$ composing projector Ξ, which we initially defined as follows:

$$ \varOmega_{ij}^{\left( k \right)} = I \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{I - P^{\left( k \right)} }}_{j} \otimes \ldots \otimes I. $$

Given that I − P^(k) = $\sum\nolimits_{l \ne k}^{N} {P^{\left( l \right)} }$, we can rewrite the above projector as the following sum:

$$ \varOmega_{ij}^{\left( k \right)} = \mathop \sum \limits_{l \ne k}^{N} I \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{P^{\left( l \right)} }}_{j} \otimes \ldots \otimes I, $$

and, consequently, the projectors Γ_ij from (17) will have the following form:

$$ \varGamma_{ij} = \mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l \ne k}^{N} I \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{P^{\left( l \right)} }}_{j} \otimes \ldots \otimes I. $$

The operator Ξ is calculated by taking the product of all the above expressions for any i, j:

$$ \varXi = \mathop \prod \limits_{i,j = 1}^{N} \mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l \ne k}^{N} I \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{P^{\left( l \right)} }}_{j} \otimes \ldots \otimes I $$

Computing this product directly may seem a daunting task, due to an enormous number of possible combinations, since we are calculating here the product of N(N − 1) sums, each of which consists of N(N − 1) elements, so the number of different combinations to multiply is the staggering [N(N − 1)]^N(N−1). However, the result of this gigantic number of multiplications may be easier to predict than it seems. First off, we should notice that the product of two projectors P⁽ⁱ⁾P^(j) gives 0 when i ≠ j and P⁽ⁱ⁾ when i = j. This actually ensures that each non-zero component in the resulting sum that constitutes projector Ξ will have the form of the tensor product of N projectors P⁽ⁱ⁾ without any identity operators (since for each slot in the tensor product there is some Γ_ij which has this slot filled by some operator P^(k), and no product of these operators can give I). Moreover, we can easily check that this product has to consist of distinct projectors (no repetitions are allowed). Suppose, to the contrary, that one component in the sum constituting Ξ has the form $\ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{j} \otimes \ldots$. But this would mean that within the components of the sum constituting projector Γ_ij there is a combination of the form $I \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{i} \otimes \ldots \otimes \underbrace {{P^{\left( k \right)} }}_{j} \otimes \ldots \otimes I$, and this is impossible, given the way we defined Γ_ij. Hence Ξ must contain only products of projectors P⁽ⁱ⁾ with no repetition.

That such products must occur in the decomposition of Ξ can be shown directly. Let α_ij be the following selected component of the sum Γ_ij:

$$ \alpha_{ij} = I \otimes \ldots \otimes \underbrace {{P^{\left( i \right)} }}_{i} \otimes \ldots \otimes \underbrace {{P^{\left( j \right)} }}_{j} \otimes \ldots \otimes I $$

It is easy to observe that the product of all α_ij’s will be exactly the required combination:

$$ \mathop \prod \limits_{i,j = 1}^{N} \alpha_{ij} = P^{\left( 1 \right)} \otimes P^{\left( 2 \right)} \otimes \ldots \otimes P^{\left( N \right)} . $$

However, projector Ξ is obviously symmetric with respect to permutations of places, hence the sum has to contain all permutations of the above tensor product. Consequently, we have established that Ξ has to have the following, simple form:

$$ \varXi = \mathop \sum \limits_{\sigma } P^{\sigma \left( 1 \right)} P^{\sigma \left( 2 \right)} \otimes \ldots \otimes P^{\sigma \left( N \right)} $$

from which it immediately follows that all vectors |a_σ(1)〉|a_σ(2)〉 … |a_σ(N)〉 lie within the range of Ξ. And this in turn proves by linearity that the symmetric and antisymmetric vectors $\mathop \sum \limits_{\sigma } \left| {a_{\sigma \left( 1 \right)} } \right\rangle \left| {a_{\sigma \left( 2 \right)} } \right\rangle \ldots \left| {a_{\sigma \left( N \right)} } \right\rangle$ and $\mathop \sum \limits_{\sigma } {\text{sgn}}(\sigma )\left| {a_{\sigma \left( 1 \right)} } \right\rangle \left| {a_{\sigma \left( 2 \right)} } \right\rangle \ldots \left| {a_{\sigma \left( N \right)} } \right\rangle$ are also eigenvectors of Ξ.