Abstract
This paper investigates set-theoretical semantics for logics that contain unary connectives, which can be viewed as modalities. Indeed, some of the logics we consider are closely related to linear logic. We use insights from the relational semantics of relevance logics together with a new version of the squeeze lemma in our semantics for logics with disjunction (but no conjunction). The ideal-based semantics, which takes co-theories to be situations, dualizes the theory-based semantics for logics with conjunction (but no disjunction).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Semantical considerations may suggest that \(\,!\,\) and \(\lozenge \), on one hand, plus \(\,?\,\) and \(\square \), on the other hand, are better pairings (cf. Bimbó 2007; Bimbó and Dunn 2008). However, both the proof-theoretical and the semantic analogies are mere analogies, which we underline by not using a notation (like \(\square \) or \(\lozenge \)) that have deeply ingrained connotations in modal logic.
- 2.
The notation used here is the same notation that we used in Bimbó (2017).
- 3.
- 4.
For example,
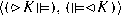 is a pair that may be included or omitted. The cut theorem for the calculuses here is Theorem 15 in Bimbó (2017). The proof of the cut theorem in [Bimbó 2015a, §3] is triple-inductive proof for the intensional part of our calculuses with modalized structural rules. See also Chap. 7 in Bimbó (2015b).
is a pair that may be included or omitted. The cut theorem for the calculuses here is Theorem 15 in Bimbó (2017). The proof of the cut theorem in [Bimbó 2015a, §3] is triple-inductive proof for the intensional part of our calculuses with modalized structural rules. See also Chap. 7 in Bimbó (2015b). - 5.
The duality between filters and ideals, which is rooted in the duality of \(\wedge \) and \(\vee \), has a storied past in logic (see Halmos 1962, p. 22 and Dunn 2019, p. 28). Our semantics are also motivated by semantics for relevance logics in a broad sense of relevance (see Avron 1984, 2014; Bimbó and Dunn 2009).
- 6.
Lowercase Greek letters range over elements of U, and we will use logical symbols in the metalanguage which may be thought—for the sake of simplicity—to be those in two-valued logic.
- 7.
As a rule, we only indicate the situation that makes a formula true in a model in the \(\vDash \) notation, and we omit mentioning \(\mathfrak {F}\) or v—to enhance readability.
- 8.
References
Avron, A. (1984). Relevant entailment - semantics and formal systems. Journal of Symbolic Logic, 49(2), 334–342.
Avron, A. (1987). A constructive analysis of \(RM\). Journal of Symbolic Logic, 52, 939–951.
Avron, A. (1988). The semantics and proof theory of linear logic. Theoretical Computer Science, 57, 161–184.
Avron, A. (1991). Using hypersequents in proof systems for non-classical logics. Annals of Mathematics and Artificial Intelligence, 4, 225–248.
Avron, A. (1996). The method of hypersequents in the proof theory of propositional non-classical logics. In W. Hodges, M. Hyland, C. Steinhorn, & J. Truss (Eds.), Logic: From Foundations to Applications (pp. 1–32). Oxford: Oxford University Press.
Avron, A. (2014). What is relevance logic? Annals of Pure and Applied Logic, 165, 26–48.
Bimbó, K. (2007). Relevance logics. In D. Jacquette (Ed.), Philosophy of Logic, Handbook of the Philosophy of Science (D. Gabbay, P. Thagard & J. Woods (Eds.)) (Vol. 5, pp. 723–789). Amsterdam: Elsevier (North-Holland). https://doi.org/10.1016/B978-044451541-4/50022-1.
Bimbó, K. (2009). Dual gaggle semantics for entailment. Notre Dame Journal of Formal Logic, 50(1), 23–41. https://doi.org/10.1215/00294527-2008-025.
Bimbó, K. (2015a). The decidability of the intensional fragment of classical linear logic. Theoretical Computer Science, 597, 1–17. https://doi.org/10.1016/j.tcs.2015.06.019.
Bimbó, K. (2015b). Proof Theory: Sequent Calculi and Related Formalisms. Boca Raton, FL: CRC Press. https://doi.org/10.1201/b17294
Bimbó, K. (2016). Some relevance logics from the point of view of relational semantics. Logic Journal of the IGPL, 24(3), 268–287. O. Arieli & A. Zamansky (Eds.) Israeli Workshop on Non-classical Logics and their Applications (IsraLog 2014). https://doi.org/10.1093/jigpal/jzw003.
Bimbó, K. (2017). On the decidability of certain semi-lattice based modal logics. In R. A. Schmidt & C. Nalon (Eds.), Automated Reasoning with Analytic Tableaux and Related Methods. Proceedings of the 26th International Conference, TABLEAUX 2017, Brasília, Brazil, September 25–28, 2017, no. 10501 (pp. 44–61). Lecture Notes in Artificial Intelligence. Switzerland: Springer Nature. https://doi.org/10.1007/978-3-319-66902-1_3.
Bimbó, K., & Dunn, J. M. (2005). Relational semantics for Kleene logic and action logic. Notre Dame Journal of Formal Logic, 46, 461–490. https://doi.org/10.1305/ndjfl/1134397663.
Bimbó, K., & Dunn, J. M. (2008). Generalized Galois Logics: Relational Semantics of Nonclassical Logical Calculi, CSLI Lecture Notes (Vol. 188). Stanford, CA: CSLI Publications.
Bimbó, K., & Dunn, J. M. (2009). Symmetric generalized Galois logics. Logica Universalis, 3(1), 125–152. https://doi.org/10.1007/s11787-009-0004-3.
Bimbó, K., & Dunn, J. M. (2015). Modalities in lattice-\(R\). (manuscript, 34 pages).
Cresswell, M., Mares, E., & Rini, A. (Eds.). (2016). Logical Modalities from Aristotle to Carnap. The Story of Necessity. Cambridge, UK: Cambridge University Press.
Dunn, J. M. (1966). The algebra of intensional logics. Ph.D. thesis, University of Pittsburgh, Ann Arbor (UMI). (Published as v. 2 in the Logic PhDs series by College Publications, London (UK), 2019.)
Dunn, J. M. (1973). A ‘Gentzen system’ for positive relevant implication, (abstract). Journal of Symbolic Logic, 38, 356–357.
Dunn, J. M. (1986). Relevance logic and entailment. In D. Gabbay & F. Guenthner (Eds.), Handbook of Philosophical Logic (1st ed., Vol. 3, pp. 117–224). Dordrecht: D. Reidel.
Dunn, J. M. (1991). Gaggle theory: An abstraction of Galois connections and residuation, with applications to negation, implication, and various logical operators. In J. van Eijck (Ed.), Logics in AI: European Workshop JELIA ’90 (Vol. 478, pp. 31–51)., Lecture Notes in Computer Science Berlin: Springer.
Dunn, J. M. (1993). Partial gaggles applied to logics with restricted structural rules. In K. Došen & P. Schroeder-Heister (Eds.), Substructural Logics (Vol. 2, pp. 63–108)., Studies in Logic and Computation Clarendon, Oxford, UK.
Dunn, J. M. (1995). Positive modal logic. Studia Logica, 55, 301–317. https://doi.org/10.1007/BF01061239.
Gentzen, G. (1964). Investigations into logical deduction. American Philosophical Quarterly, 1, 288–306.
Girard, J. Y. (1987). Linear logic. Theoretical Computer Science, 50, 1–102.
Gödel, K. (1986). Eine Interpretation des intuitionistischen Aussagenkalküls. In S. Feferman (Ed.), Collected Works (Vol. I, pp. 300–303). New York, NY and Oxford, UK: Oxford University Press and Clarendon Press.
Halmos, P. R. (1962). Algebraic Logic. New York, NY: Chelsea Publishing Company.
Kopylov, A. P. (2001). Decidability of linear affine logic. In A. R. Meyer (Ed.), Special issue: LICS 1995, Information and Computation (Vol. 164, pp. 173–198). IEEE.
Kripke, S. A. (1959). A completeness theorem in modal logic. Journal of Symbolic Logic, 24, 1–14.
Kripke, S. A. (1963). Semantical considerations on modal logic. Acta Philosophica Fennica, 16, 83–94.
Kripke, S. A. (1965). Semantical analysis of intuitionistic logic I. In J. N. Crossley & M. A. E. Dummett (Eds.), Formal Systems and Recursive Functions. Proceedings of the Eighth Logic Colloquium (pp. 92–130). Amsterdam: North-Holland.
Meyer, R. K. (1966). Topics in modal and many-valued logic. Ph.D. thesis, University of Pittsburgh, Ann Arbor (UMI)
Routley, R., & Meyer, R. K. (1973). The semantics of entailment. In H. Leblanc (Ed.), Truth, Syntax and Modality. Proceedings of the Temple University Conference on Alternative Semantics (pp. 199–243). Amsterdam: North-Holland.
Acknowledgements
I am grateful to Anna Zamansky and Ofer Arieli, the editors of the volume, for inviting me to contribute a paper. I would like to thank the organizers of and the audiences at IsraLog 2017 (The Third Israeli Workshop on Non-Classical Logics and their Applications) and AAL 2018 (2018 Annual Meeting of the Australasian Association for Logic) where I presented talks related to this paper. I am also grateful to the IU Logic Group at Indiana University–Bloomington for letting me talk about the results in this paper in November 2019. The research reported in this paper was funded by an Insight Grant (SSHRC IG #435–2014–0127) awarded by the Social Sciences and Humanities Research Council of Canada.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bimbó, K. (2021). Interpretations of Weak Positive Modal Logics. In: Arieli, O., Zamansky, A. (eds) Arnon Avron on Semantics and Proof Theory of Non-Classical Logics. Outstanding Contributions to Logic, vol 21. Springer, Cham. https://doi.org/10.1007/978-3-030-71258-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-71258-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-71257-0
Online ISBN: 978-3-030-71258-7
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


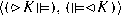 is a pair that may be included or omitted. The cut theorem for the calculuses here is Theorem 15 in Bimbó (
is a pair that may be included or omitted. The cut theorem for the calculuses here is Theorem 15 in Bimbó (