The true futures

Abstract

In this paper various branching time semantics are compared with the aim of clarifying the role of true futures of counterfactual moments, that is, true futures of moments outside the true chronicle. First we give an account of Arthur Prior’s Ockhamistic semantics where truth of a formula is relative to a moment and a chronicle. We prove that this is equivalent to a version of a semantics put forward by Thomason and Gupta where truth is relative to a moment and what is called a chronicle function which assigns a chronicle to each moment. Later we discuss how a semantic theory considered by Belnap and Green may be formalised. It comes about by assuming a chronicle function to be given once and for all. However, this semantics invalidates an intuitively valid formula, so we present an alternative semantics where the formula in question is valid. Furthermore, we shall exhibit an intuitively invalid formula which is invalid in our alternative semantics, but which is valid in Prior’s Ockhamistic semantics. So we can conclude that Prior’s Ockhamistic validity does not imply validity in the alternative semantics. On the other hand, the converse implication does hold, as we shall prove. Summary of mathematical results: We have proved that Prior’s Ockhamistic semantics has the same valid formulas as Thomason and Gupta’s semantics, and we have proved that Prior’s Ockhamistic semantics has strictly more valid formulas than the alternative semantics.

1 Introduction

The present paper is concerned with certain branching time semantics which involve a notion of true future. The semantics in question are compared with the aim of making clear the role of true futures of counterfactual moments. A counterfactual moment is a moment outside the true chronicle, that is, the true course of events. The paper is a revised and extended version of the workshop paper Braüner et al. (1998).

In the next section of this paper we give an account of Prior’s Ockhamistic semantics. See also Prior (1967, p. 126 ff). Here truth of a formula is relative to a moment as well as a chronicle—which is to be understood as truth being relative to a possible future of the moment in question.

In Sect. 3 we give an account of a version of a semantics put forward by Thomason and Gupta (1980). Here truth of a formula is relative to a moment as well as what is called a chronicle function, which assigns a chronicle to each moment—this is to be understood as truth being relative to a true future of each moment. This semantics is equivalent to Prior’s Ockhamistic semantics, which is proved in the Appendix, using a clarified and detailed version of a proof originally given in Braüner et al. (1998). The reason why the two semantics are equivalent is that true futures of counterfactual moments, that is, moments outside the true chronicle, do not matter in our version of Thomason and Gupta’s semantics (contrary to the original semantics of Thomason and Gupta (1980), since it also includes counterfactual implication).

Then, in Sect. 4 we give an account of a semantic theory considered by Belnap and Green (1994). It comes about by assuming that a chronicle function is given once and for all. We discuss how such an assumption might give rise to a formal semantics. However, this semantics has the problem that it invalidates the intuitively valid formula $\phi \rightarrow HF \phi$, where $\phi$ is an arbitrary formula.

In Sect. 5 we describe an alternative semantics, which we call the Braüner et al. (1998)-semantics, since it was originally put forward in that paper. Compared to the other semantics given in this paper, it is a notable feature that the formula $\phi \rightarrow HF \phi$ is valid here, and furthermore, true futures of counterfactual moments are taken into account as appropriate. To demonstrate this, we shall give a pair of examples of statements, symbolized $\phi$ and $\psi$, which are not logically equivalent with respect to the Braüner et al. (1998)-semantics, but which differ only with respect to what they say will happen in the future of a counterfactual moment. However, the formulas $\phi$ and $\psi$ are logically equivalent with respect to Prior’s Ockhamistic semantics. Intuitively, we find that $\phi$ and $\psi$ should not be counted as logically equivalent since they do not say the same about what will happen in the future of the counterfactual moment in question. Hence, the Priorean Ockhamistic semantics validates the intuitively invalid formula $\phi \leftrightarrow \psi$ which is invalid with respect to our Braüner et al. (1998)-semantics. We find that this observation is interesting on its own right, but it also enables us to conclude that Prior’s Ockhamistic validity does not imply validity in the sense of the Braüner et al. (1998)-semantics. On the other hand, the converse implication does hold, as we shall prove. In other words, we have proved that there is a strict inclusion between the sets valid formulas in the two logics.

In the concluding section we make some remarks on further work.

1.1 Related work

The different semantics presented in this paper are part of a long and still ongoing discussion about semantics for future contingents. Using military terminology, this discussion has even been called a battle by some authors, in particular the author of the paper Wawer (2014), which describes the battlefield anno 2014. The paper gives the following description of the weapons employed in this battle:

The attacks usually take the form of examples of sentences which sound intuitive and which are valid in Ockhamism, but are invalidated by one or other of the TRL semantics [what we above called chronicle functions]. The defenses are attempts to restore the validity of these sentences while preserving the core of the TRL intuition. (Wawer, 2014, p. 368)

The terminology of Wawer (2014) can also be applied to the development after 2014, in particular in connection with debates about Molinism, a theological system aiming at reconciling divine foreknowledge with human free will, and having a notion of time similar to TRL models. Analyses of Molinism in terms of TRL models have been put forward in papers by Øhrstrøm and Hasle (2020) and references therein. Many further papers have been published, for example the paper Florio and Frigerio (2020), which attacks the criticisms of Molinism and TRL models raised in the paper Restall (2011). Further recent discussions on this issue can be found in for example Florio and Frigerio (2019); Sandu et al. (2018); Santelli (2022); Wawer (2022).

The goal of the present paper is not really to initiate a new battle, but rather to go back to Braüner et al. (1998) and flesh out the more mathematical logical details of what was going on, in particular the mathematical relationships between some of the different TRL models at stake: Prior’s Ockhamistic semantics, Thomason and Gupta’s semantics, and our alternative Braüner et al. (1998)-semantics in Sect. 5.

2 Prior’s Ockhamistic semantics

In this section, we shall give an account of a branching time semantics which was put forward by Prior (1967, p. 126 ff). Our presentation of this semantics is guided by the presentation in Braüner et al. (1998), but similar presentations can be found many places, for example Øhrstrøm and Hasle (2020). Prior’s aim with the semantics was to formalise some ideas of William of Ockham (ca. 1285–1349) concerning human freedom and divine foreknowledge. See William of Ockham (1963). Furthermore, we shall consider a pair of examples of statements from natural language that makes it clear that Prior’s Ockhamistic semantics does take into account the true future with respect to which truth is relative.

To define Prior’s Ockhamistic semantics, we need a set T equipped with a relation <. The elements of T are to be thought of as moments and < as the earlier-later relation. It is assumed that < is irreflexive and transitive, and furthermore, to account for the branchingness of time it is assumed that it is backwards linear. The relation < is said to be backwards linear if and only if

$$\begin{aligned} \forall t,u,v \, ( (t< u \wedge v< u) \Rightarrow (t< v \vee v< t \vee t=v)). \end{aligned}$$

A pair $(T,<)$ is called a frame. An important feature of the semantics is a notion of “temporal routes” or “temporal branches” which are to be thought of as possible courses of events. We shall call such branches chronicles.¹ Formally, a chronicle is a maximal linear subset of $(T,<)$. The set of chronicles induced by $(T,<)$ will be denoted ${{{\mathcal {C}}}}(T,<)$.

In the rest of the paper, we let p, q, ... range over propositional letters and we let the metavariables $\phi$, $\psi$, ... range over formulas. We need a function V which assigns a truth value V(t, p) to each pair consisting of an element t of T and a propositional letter p. To increase readability, we shall violate notation as follows: Strictly speaking, V is a function with range $\{T,F\}$, but we write V(t, p) instead of $V(t,p)=T$, etc.

A triple $(T,<,V)$ is called a model. Given a model, truth is relative to a moment as well as a chronicle to which the moment belongs. This is to be understood as truth being relative to a true future of the moment in question. By induction, we define the valuation function $V_{{ \! Ock}}$ as follows:

$$\begin{aligned} \begin{array}{rcl} V_{{ \! Ock}}(t,c,p) &{} \text{ iff } &{} V(t,p) \\ V_{{ \! Ock}}(t,c, \phi \wedge \psi ) &{} \text{ iff } &{} V_{{ \! Ock}}(t,c,\phi ) \text{ and } V_{{ \! Ock}}(t,c,\psi ) \\ V_{{ \! Ock}}(t,c, \lnot \phi ) &{} \text{ iff } &{} \text{ not } V_{{ \! Ock}}(t,c,\phi ) \\ V_{{ \! Ock}}(t,c,P\phi ) &{} \text{ iff } &{} V_{{ \! Ock}}(t',c,\phi ) \text{ for } \text{ some } t'<t \\ V_{{ \! Ock}}(t,c,F\phi ) &{} \text{ iff } &{} V_{{ \! Ock}}(t',c,\phi ) \text{ for } \text{ some } t'>t \text{ where } t' \in c\\ V_{{ \! Ock}}(t,c,\square \phi ) &{} \text{ iff } &{} V_{{ \! Ock}}(t,c',\phi ) \text{ for } \text{ all } c' \in {{\mathcal {C}}}(T,<) \text{ where } t \in c' \end{array} \end{aligned}$$

So $V_{{ \! Ock}}(t,c,\phi )$ means that $\phi$ is true at the moment t in the chronicle c. A formula $\phi$ is said to be Ockhamist-true in a model $(T,<,V)$ if and only if for any moment t and chronicle c such that $t \in c$, it is the case that $V_{{ \! Ock}}(t,c,\phi )$. A formula $\phi$ is said to be Ockhamist-valid if and only if $\phi$ is Ockhamist-true in any model $(T,<,V)$. It is for example easy to check that the formula $\phi \rightarrow HF\phi$ (where $H\psi$ is an abbreviation for $\lnot P \lnot \psi$), is Ockhamist-valid. This formula expresses what is known as the principle of retrogradation of truth.

Note that in Prior’s Ockhamistic semantics, the truth-value of a propositional letter $V_{{ \! Ock}}(t,c,p)$ is equal to V(t, p) , hence, the truth-value of a propositional letter is independent of the choice of chronicle—in Prior’s words, such propositional letters have no trace of futurity in them, cf. Prior (1967, p. 124). From this interpretation of propositional letters, it follows that the formula $q \rightarrow \square q$ is valid (notice that q is a propositional letter). This formula is in good accordance with the medieval dictum “unumquodque, quando est, oportet esse” (“anything, when it is, is necessary”), see Rescher and Urquhart (1971, p. 191). It should be mentioned that Prior also considered a second sort of propositional letters which are interpreted relative to a moment and a chronicle to which the moment belongs, thus allowing dependence on the future. If b is a propositional letter with that second interpretation, then the formula $b \rightarrow \square b$ is not valid. In our semantics we have just included the propositional letters that are interpreted independently of the future, one reason being that they are the ones needed in our example statements in Subsect. 5.1, like the statement ‘Coin number one comes up tails’ which clearly do not depend on the future.

It may be doubted whether Prior’s Ockhamistic logic is in fact an accurate representation of the temporal logical ideas propagated by William of Ockham, who presumably would accept an idea of absolute truth and say that a future contingent statement like $F\phi$ can be true at a moment t without being relativised to a chronicle. This is an interesting historical discussion, but we shall leave it here, see Øhrstrøm and Hasle (2020).

3 Thomason and Gupta’s semantics

In this section, we shall compare the Ockhamistic semantics given by Prior to a version of a semantics given by Thomason and Gupta (1980).² Our presentation is guided by the presentation in Braüner et al. (1998). An essential difference between Prior’s Ockhamistic semantics and Thomason and Gupta’s semantics is that in the former semantics, truth is relative to a moment as well as a chronicle whereas in the latter semantics, truth is relative to a moment as well as what is called a chronicle function, which to each moment assigns a chronicle. It can be proved that the two semantics are equivalent in the sense that they validate the same formulas. This is the case because true futures of counterfactual moments do not matter in the semantics—despite the fact that truth is relative to a moment as well as a chronicle function. It should be mentioned that besides the usual Ockhamistic connectives, the semantics given in Thomason and Gupta’s paper also includes counterfactual implication—in such a context true futures of counterfactual moments do make a difference.

A formal account of Thomason and Gupta’s semantics is based on the same notion of a model as the one used previously in this paper. So we need a set T equipped with an irreflexive, transitive and backwards linear relation < together with a function V which assigns a truth value to each pair consisting of a moment and a propositional letter. Furthermore, it involves a relation on T relating “copresent” (or “pseudo-simultanous”) moments and also certain additional machinery to interpret counterfactual implication. Here we do not consider counterfactual implication so we shall disregard such machinery, and moreover, we adapt Thomason and Gupta’s semantics to the previous setting of the present paper where no notion of copresentness is taken into account.

In the Priorean Ockhamist semantics, truth is relative to a moment and a chronicle to which the moment belongs. In Thomason and Gupta’s semantics, truth is relative to a moment and a chronicle function. A chronicle function³ is a function C which assigns to each moment a chronicle such that the following two conditions are satisfied:

(C1):

$\forall t \, (t \in C(t))$.

(C2):

$\forall t,u \, ((t<u \wedge u \in C(t)) \Rightarrow C(t)=C(u))$.

The first condition says that the present moment is actual. The second condition says that any moment which will be actual has the same true future as the present moment. The definition of truth of a formula as relative to a moment and a chronicle function is to be understood as truth being relative to a moment as well as a true future of each moment.

We need a further definition: Given a moment t, a chronicle function C is said to be normal at t if and only if

$$\begin{aligned} \forall u<t \, (C(u) = C(t)). \end{aligned}$$

We shall make the assumption that the chronicle function with respect to which truth is relative, is normal at the moment with respect to which truth is relative. The notion of a normal chronicle function can be traced back to Thomason and Gupta’s paper (1980).⁴ We let ${{\mathcal {N}}}(t)$ denote the set of chronicle functions which are normal at the moment t. Given the conditions (C1) and (C2), the condition of normality at t given above is equivalent to

$$\begin{aligned} \forall u<t \, (t \in C(u)). \end{aligned}$$

Hence, normality says that the present moment has always been going to be actual. Without restricting attention to chronicle functions normal at a given moment, the intuitively valid formula $\phi \rightarrow HF \phi$ would not be valid.

We want truth to be relative to moment and a chronicle function normal at the moment in question, but how should $\square \phi$ be interpreted? As Thomason and Gupta (1980) explain in p. 311, one should not simply say that $\square \phi$ is true at t with respect to C normal at t if and only if $\phi$ is true at t with respect to all chronicle functions $C'$ normal at t. This is so because $\square \phi$ is supposed to say that $\phi$ holds no matter how things will be. Hence, $C'$ should differ from C at most at t and moments in the future of t. It follows from normality at t that $C'$ also has to be allowed to differ from C at moments in the past of t. This leads to the following definition: The chronicle functions C and $C'$ are said to differ at most at t and its past and future if and only if

$$\begin{aligned} \forall u \, ((u \ne t \wedge u \nless t \wedge t \nless u) \Rightarrow C(u) = C'(u)). \end{aligned}$$

We let $\Delta _{P,F}(t,C)$ denote the set of chronicle functions which differ from C at most at t and its past and future. By induction, we define the valuation function V as follows:

$$\begin{aligned} V(t,C,p)&\text{ iff }&V(t,p) \\ V(t,C, \phi \wedge \psi )&\text{ iff }&V(t,C,\phi ) \text{ and } V(t,C,\psi ) \\ V(t,C, \lnot \phi )&\text{ iff }&\text{ not } V(t,C,\phi ) \\ V(t,C,P\phi )&\text{ iff }&V(t',C,\phi ) \text{ for } \text{ some } t'<t \\ V(t,C,F\phi )&\text{ iff }&V(t',C,\phi ) \text{ for } \text{ some } t'>t \text{ where } t' \in C(t) \\ V(t,C,\square \phi )&\text{ iff }&V(t,C',\phi ) \text{ for } \text{ all } C' \in \mathcal{N}(t) \cap \Delta _{P,F}(t,C) \end{aligned}$$

A formula $\phi$ is said to be true in a model $(T,<,V)$ if and only if for any moment t and chronicle function C normal at t, it is the case that $V(t,C,\phi )$. A formula $\phi$ is said to be valid if and only if $\phi$ is true in any model $(T,<,V)$.

As indicated earlier, our semantics is a simplified version of a semantics given by Thomason and Gupta (1980), in particular, our language does not include counterfactual implication, and we ignore associated semantic machinery in the form of a copresent relation. And importantly, our interpretation of $\square$, that is, the clause for $\square$ above, deviates from Thomason and Gupta’s original interpretation, which involves the copresent relation.⁵

As mentioned earlier, it can be proved that the notion of validity given above is equivalent to the Priorean notion of Ockhamistic validity. A proof can be found in the Appendix.

4 Belnap and Green’s argument

In the interesting paper, Belnap and Green (1994) first consider a semantic theory where a true chronicle is given once and for all. They call such a chronicle TRL (Thin Red Line). Belnap and Green argue that this semantic theory is unable to give an account of certain statements from natural language in which there are references to true futures of counterfactual moments. This is remedied by assuming that instead of just one true chronicle, a true chronicle for each moment is given once and for all, that is, a chronicle function. But also in this case problems apparently crop up: Either the frame is forced to be forwards linear or certain intuitively valid formulas are invalidated. Following Braüner et al. (1998), we in this section discuss how Belnap and Green’s argument may be formalised.

Belnap and Green do not give a formal semantics, but it is clear that they interpret tenses by moving in the appropriate direction along the chronicle assigned to the moment with respect to which truth is relative. They discuss which conditions a function C assigning chronicles to moments has to satisfy, but rather than condition (C2), they begin by assuming the stronger condition

$$\begin{aligned} \forall t,u \, (t<u \Rightarrow C(t)=C(u)) \end{aligned}$$

to be satisfied (which amounts to the function being normal at every moment of the frame). This is problematic because it forces the earlier-later relation to be forwards linear.⁶ To avoid this unpalatable conclusion, their next step is simply to leave out the above mentioned condition. Thus, the function assigning chronicles to moments is now only assumed to satisfy condition (C1). But then the intuitively valid formulas $FF\phi \rightarrow F\phi$ and $\phi \rightarrow PF\phi$ are invalidated. This makes Belnap and Green conclude:

We have considered two alternatives to the open future doctrine, and have found each of them wanting. (Belnap & Green, 1994, p. 380)

Below we shall discuss how Belnap and Green’s ideas might have been formalised had they taken the appropriate condition on the function assigning chronicles to moments.

In what follows, we shall therefore restrict our attention to chronicle functions in the previous sense of this paper unless otherwise is indicated, thus, it is assumed that conditions (C1) and (C2) are satisfied. And given a chronicle function C and a moment of evaluation t, it is assumed that tenses are interpreted in a recursive way by moving in the appropriate direction along the chronicle C(t). It is not clear how the interpretation of the necessity operator goes in Belnap and Green’s semantic theory, but given that $\square \phi$ is supposed to say that $\phi$ holds no matter how things will be in the future of the moment t, it seems that the recursive semantics of $\square \phi$ has to take into account chronicle functions different from the once and for all given chronicle function C (if that was not the case, then it is not clear how the semantics of $\square \phi$ could take into account other chronicles than C(t)).⁷

In accordance with this line of reasoning, we let truth be relative to a moment as well as a chronicle function. This suggests a semantics like the one put forward by Thomason and Gupta except that $\square \phi$ is true at t with respect to C if and only if $\phi$ is true at t with respect to all chronicle functions $C'$ such that $C'$ differ from C at most at the moment t. Formally, the chronicle functions C and $C'$ are said to differ at most at t if and only if

$$\begin{aligned} \forall u \, (u \ne t \Rightarrow C(u) = C'(u)). \end{aligned}$$

We let $\Delta (t,C)$ denote the set of chronicle functions which differ from C at most at t (and which satisfy conditions (C1) and (C2) since we are only considering such chronicle functions in the present semantics, as mentioned earlier). Then the valuation function V is defined as follows:

$$\begin{aligned} V(t,C,p)&\text{ iff }&V(t,p) \\ V(t,C, \phi \wedge \psi )&\text{ iff }&V(t,C,\phi ) \text{ and } V(t,C,\psi ) \\ V(t,C, \lnot \phi )&\text{ iff }&\text{ not } V(t,C,\phi ) \\ V(t,C,P\phi )&\text{ iff }&V(t',C,\phi ) \text{ for } \text{ some } t'<t \\ V(t,C,F\phi )&\text{ iff }&V(t',C,\phi ) \text{ for } \text{ some } t'>t \text{ where } t' \in C(t) \\ V(t,C,\square \phi )&\text{ iff }&V(t,C', \phi ) \text{ for } \text{ all } C' \in \Delta (t,C) \end{aligned}$$

A formula $\phi$ is said to be valid if and only if $\phi$ is true in any model $(T,<,V)$, that is, it is the case that $V(t,C,\phi )$ for any moment t and chronicle function C. Note that the notion of normality is not involved in this semantics.

Now, it is straightforward to check that the formula $FF\phi \rightarrow F\phi$ is valid with respect to the semantics given above. However, the formula $\phi \rightarrow HF\phi$ is invalid: If we instantiate $\phi$ to the propositional letter q, then the obtained formula $q \rightarrow HFq$ is false at the upper-most moment of the following chronicle function equipped model

Note that we have used a thick line to represent the future part of the chronicle assigned to a moment (the past part needs no representation as it is uniquely determined). Similarly, the instance $q \rightarrow PFq$ of the formula $\phi \rightarrow PF\phi$ is false at the upper-most moment of the above chronicle function equipped model.

Given our intuitive Ockhamist reading of the future tense operator, we want the formula $\phi \rightarrow HF\phi$ to be valid, but since it is invalidated by the above semantics, we conclude that the semantics is unsatisfactory.

5 The alternative Braüner et al. (1998)-semantics

What we are after in this section is a semantics which does validate the formula $\phi \rightarrow HF\phi$, and furthermore, we want a semantics which does give an appropriate account of true futures of counterfactual moments. With these goals in mind we introduce a semantics which is alternative to Belnap and Green’s semantics described in the previous section. We call it the Braüner et al. (1998)-semantics, after the paper where it was put forward. Moreover, we shall give a pair of examples of statements from natural language which shows that the Braüner et al. (1998)-semantics does indeed give an account of true futures of counterfactual moments. These considerations give rise to an intuitively invalid formula which is invalid in the Braüner et al. (1998)-semantics, but which is valid in Prior’s Ockhamistic semantics. This observation is obviously interesting on its own right, but it also enables us to conclude that Prior’s Ockhamist validity does not imply validity in the Braüner et al. (1998)-semantics. On the other hand, the converse implication does hold, as we shall prove.

In what follows, we shall give a formal account of the Braüner et al. (1998)-semantics. What we do is we take the semantics of the last section where truth is relative to a moment and a chronicle function. Thus, conditions (C1) and (C2) are satisfied. We then add the condition that the chronicle function has to be normal at the moment in question. This makes the resulting semantics validate the formula $\phi \rightarrow HF\phi$. The restriction to normal chronicle functions forces us to change the semantics of necessity such that it takes into account chronicle functions differing from the given chronicle function not only at the moment with respect to which truth is relative but at moments in the past of the moment with respect to which truth is relative. Thus, the key feature of the semantics is that $\square p$ is true at t with respect to C normal at t if and only if p is true at t with respect to all chronicle functions $C'$ normal at t such that $C'$ differ from C at most at the moment t and its past. Formally, the chronicle functions C and $C'$ are said to differ at most at t and its past if and only if

$$\begin{aligned} \forall u \, (( u \nleq t) \Rightarrow C(u) = C'(u)). \end{aligned}$$

We let $\Delta _{P}(t,C)$ denote the set of chronicle functions which differ from C at most at t and its past. We now define the valuation function V as follows:

$$\begin{aligned} \begin{array}{rcl} V(t,C,p) &{} \text{ iff } &{} V(t,p) \\ V(t,C, \phi \wedge \psi ) &{} \text{ iff } &{} V(t,C,\phi ) \text{ and } V(t,C,\psi ) \\ V(t,C, \lnot \phi ) &{} \text{ iff } &{} \text{ not } V(t,C,\phi ) \\ V(t,C,P\phi ) &{} \text{ iff } &{} V(t',C,\phi ) \text{ for } \text{ some } t'<t \\ V(t,C,F\phi ) &{} \text{ iff } &{} V(t',C,\phi ) \text{ for } \text{ some } t'>t \text{ where } t' \in C(t) \\ V(t,C,\square \phi ) &{} \text{ iff } &{} V(t,C',\phi ) \text{ for } \text{ all } C' \in \mathcal{N}(t) \cap \Delta _{P}(t,C) \end{array} \end{aligned}$$

A formula $\phi$ is said to be Braüner et al. (1998)-valid if and only if $\phi$ is true in any model $(T,<,V)$, that is, it is the case that $V(t,C,\phi )$ for any moment t and chronicle function C normal at t. When the context is clear, we shall just talk about validity instead of Braüner et al. (1998)-validity.

It is straightforward to check that both of the formulas $FF\phi \rightarrow F\phi$ and $\phi \rightarrow HF\phi$ are valid wrt. the Braüner et al. (1998)-semantics. In fact, note that all standard axioms of linear tense logic are valid with respect to the Braüner et al. (1998)-semantics, and also, all rules of linear tense logic preserve validity. In this sense all minimal reasoning principles of linear tense logic are adhered to. Note also that all axioms of the modal logic S5 are valid and all rules of S5 preserve validity (for an introduction to S5, see Hughes & Cresswell, 1968).

5.1 Examples

We shall now give a pair of examples of statements from natural language which shows that the Braüner et al. (1998)-semantics does give an appropriate account of true futures of counterfactual moments. The scenario is similar to a scenario considered by Belnap and Green (1994). Suppose a coin (coin number one) is tossed. If it comes up tails, another coin (coin number two) is tossed. Consider the two statements

Coin number one will come up heads. It is possible, though, that it will come up tails, and then later (*) coin number two will come up tails (though coin number two could come up heads).

and

Coin number one will come up heads. It is possible, though, that it will come up tails, and then later (*) coin number two will come up heads (though coin number two could come up tails).

The examples only differ with respect to what they say will happen in the future of a counterfactual moment: At (*) the first example says that tails will happen and heads might happen whereas the second example says that heads will happen and tails might happen. We shall symbolise the examples as respectively

$$\begin{aligned} Fp' \wedge \lozenge F(p \wedge Fq \wedge \lozenge Fq') \end{aligned}$$

and

$$\begin{aligned} Fp' \wedge \lozenge F(p \wedge Fq' \wedge \lozenge Fq) \end{aligned}$$

where p and $p'$ stand for respectively ‘Coin number one comes up tails’ and ‘Coin number one comes up heads’, and analogously, q and $q'$ stand for respectively ‘Coin number two comes up tails’ and ‘Coin number two comes up heads’. As usual, $\lozenge \phi$ is an abbreviation for $\lnot \square \lnot \phi$. Intuitively, we find that the two formulas displayed above should not be counted as logically equivalent since they do not say the same about what will happen at (*). And they are indeed distinguished by Braüner et al. (1998)-semantics.

According to the notion of possibility involved in the Braüner et al. (1998)-semantics, the first formula displayed above is true at the left-most moment of the chronicle function equipped model

if and only if the formula $F(p \wedge Fq \wedge \lozenge Fq')$ satisfies the condition that it is true at the left-most moment of at least one of the following two chronicle function equipped models

Clearly, this condition is satisfied. Analogously, the truth of the second formula displayed above can be reduced to a condition regarding the truth of the formula $F(p \wedge Fq' \wedge \lozenge Fq)$. But this time the condition is not satisfied. So the formula

$$\begin{aligned} (Fp' \wedge \lozenge F(p \wedge Fq \wedge \lozenge Fq')) \leftrightarrow (Fp' \wedge \lozenge F(p \wedge Fq' \wedge \lozenge Fq)) \end{aligned}$$

is not valid in the Braüner et al. (1998)-semantics. But this formula is clearly valid with respect to Prior’s Ockhamistic semantics as defined in Sect. 2.⁸ From this we conclude that Ockhamist-validity does not imply validity in the sense given above. Furthermore, we note that Prior’s Ockhamist semantics validates an intuitively invalid formula which is invalid in the Braüner et al. (1998)-semantics.

The fact that the two example sentences above are distinguished by the Braüner et al. (1998)-semantics makes clear that true futures of counterfactual moments do matter. In this sense our semantics makes more distinctions than Prior’s Ockhamistic semantics, that is, it is more fine-grained.

Also, according to the Braüner et al. (1998)-semantics, the occurrences of ‘possible’ in the example sentences refer to the possible outcomes of the first toss (that is, heads or tails) rather than all the possible sequences of outcomes of tosses (that is, heads, tails followed by heads or tails followed by tails). This is made clear by the fact, cf. above, that the occurrences of ‘possible’ are interpreted by quantifying over exactly two chronicle functions, namely one for each possible outcome of the toss of coin number one. The outcome of the toss of coin number two is, on the other hand, kept fixed. We find that this is in accordance with our intuitive understanding of the example statements. In this sense the notion of possibility involved in the Braüner et al. (1998)-semantics refers to what might happen now rather than what might happen from now on in general, thus, it may be called ‘immediate possibility’.

Another formula which is valid in Prior’s Ockhamistic semantics, but not in ours, is the following

$$\begin{aligned} F \lozenge Fp \rightarrow \lozenge FFp \end{aligned}$$

(note that in the context of dense time, this formula is equivalent to $F \lozenge Fp \rightarrow \lozenge Fp$). It is easy to generate a counter-model to this formula. We are aware that many other authors, for example the authors of Ciuni and Proietti (2019), find that this formula is intuitively valid, but on the other hand, the invalidity of the formula in the Braüner et al. (1998)-semantics is in line with the fine-grainedness of the semantics, allowing the emergence of possibility in time.

5.2 Our Braüner et al. (1998)-validity implies Prior’s Ockhamist validity

The example statements of the previous subsection show that Ockhamist-validity does not imply Braüner et al. (1998)-validity. However, the converse is the case: If a formula is valid our Braüner et al. (1998)-semantics, then it is also valid in Prior’s Ockhamistic semantics, which we shall prove in what follows. This result is in line with our semantics being more fine-grained, having more countermodels than the Priorean Ockhamist semantics.

The strategy of our proof is to define for each Priorean Ockhamist model $(T,<,V)$ a new model $(T^{\star },<^{\star },V^{\star })$ equipped with a chronicle function $C^{\star }$ with the following property: For any $t \in T$ and $c \in {{\mathcal {C}}}(T,<)$ where $t \in c$ there exists a $t ^{\star } \in T^{\star }$ at which $C^{\star }$ is normal such that $V(t,c,\phi )$ is equivalent to $V^{\star }(t^{\star },C^{\star },\phi )$ for any formula $\phi$.

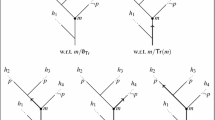
The idea underlying the definition is best explained by considering an example: The frame

can be equipped with a chronicle function in two ways

where the letter attached to a moment is a name of the moment in question (not a propositional letter true at the moment as previously in this paper). In each case there is a moment in the future of t which is not “reachable” from t in the sense that it does not belong to the chronicle assigned to t by any chronicle function differing from the given chronicle function at most at the moment t and its past. In the case on the left it is w and in the case on the right it is v. But if we copy the parts of the two frames which are in the future of t and extend the chronicle functions to the copies such that the opposite choice is made in each case, then we obtain

In each of the two cases every moment in the future of t has the property that at least one of the two versions of it is reachable from t. In the case on the left v and $w'$ are reachable and in the case on the right w and $v'$ are reachable. The moments u and $u'$ are reachable in both cases.

In general, this process of copying amounts to making a version of any moment t for every possible way in which each $u \le t$ can be assigned a chronicle passing through u. Given a frame, this defines a new frame on which furthermore we can define a chronicle function such that the following “reachability property” is satisfied: Whenever $t < v$ in the given structure, at least one version of v is reachable from any version of t in the defined new structure. We have not yet talked about propositional letters, but for any moment t in the given model, we obviously take a propositional letter p to be true at any version of t in the defined new model if and only if p is true at t in the given model. Hence, for each model a new model equipped with a chronicle function is defined such that the above mentioned reachability property is satisfied.

However, it turns out that this is not enough copying. The problem is that the reachability property might be violated as the chronicle function with respect to which truth is relative is modified by the inductive definition of truth, that is, such a modification may result in “disconnected” versions of t and v, cf. above. But every formula is finite so the chronicle function can only be modified at finitely many moments and their pasts. We therefore extend the process of copying such that it amounts to making a version of any moment t for every possible way in which each $u \le t$ can be assigned a chronicle passing through u where a natural number is attached to each moment in the future of or equal to u. Given a frame, this defines a new frame on which furthermore we can define a chronicle function such that the reachability property is satisfied with respect to any chronicle function differing from the defined chronicle function at most at finitely many moments and their pasts. Again, the definition is extended from frames to models in the obvious way.

In what follows, we shall give a formal account of the process of copying discussed above. Let a model $(T,<,V)$ be given. First, for any $t \in T$, a set $\Delta (t)$ is defined:

$$\begin{aligned} \Delta (t) = \{ (c,k) | c \in {{\mathcal {C}}}(T,<) \wedge t \in c \wedge k: \{ u \in c | u \ge t \} \rightarrow {\mathbb {N}} \} \end{aligned}$$

So an element of $\Delta (t)$ is simply a chronicle to which t belongs, where a natural number is attached to each moment in the future of or equal to t. We then define a new model $(T^{\star },<^{\star },V^{\star })$. The set $T^{\star }$ is defined as follows:

$$\begin{aligned} T^{\star } = \{ (t,f) | t \in T \wedge f: \{ u | u \le t \} \rightarrow \bigcup _{u \le t} \Delta (u) \wedge \forall u \le t \, (f(u) \in \Delta (u)) \Big \} \end{aligned}$$

The relation $<^{\star }$ is defined by the stipulation

$$\begin{aligned} (t,f)<^{\star } (u,g) \text{ iff } t < u \wedge \forall v \le t \, (f(v) = g(v)) \end{aligned}$$

It is straightforward to check that $<^{\star }$ is irreflexive, transitive and backwards linear. The function $V^{\star }$ is defined by the stipulation

$$\begin{aligned} V^{\star }((t,f),q) \text{ iff } V(t,q) \end{aligned}$$

We then equip the new model $(T^{\star },<^{\star },V^{\star })$ with a chronicle function $C^{\star }$. The function $C^{\star }:T^{\star } \rightarrow {{\mathcal {C}}}(T^{\star },<^{\star })$ is defined as follows:

$$\begin{aligned} C^{\star }((t,f)) = \left\{ \left( v, x \mapsto \left\{ \begin{array}{ll} (\pi _{1}(f(t)), z \mapsto \pi _{2}(f(t))(z)) &{} \text{ if } t < x \le v\\ f(x) &{} \text{ if } x \le t \end{array} \right. \right) | v \in \pi _{1}(f(t)) \right\} \end{aligned}$$

As usual, $\pi _{1}$ and $\pi _{2}$ denote the projection functions, that is, $\pi _{1}((a,b))=a$ and $\pi _{2}((a,b))=b$ for any pair (a, b). Note in the definition above of $C^{\star }$ that $f(t) \in \Delta (t)$, so $\pi _{1}(f(t)) \in {{\mathcal {C}}}(T,<)$ such that $t \in \pi _{1}(f(t))$, and moreover,

$$\begin{aligned} \pi _{2}(f(t)): \{ u \in \pi _{1}(f(t)) | u \ge t \} \rightarrow {\mathbb {N}}. \end{aligned}$$

The definition above implies that $z \mapsto \pi _{2}(f(t))(z))$ is the restriction of the function $\pi _{2}(f(t))$ to $\{ u \in \pi _{1}(f(t)) | u \ge x \}$. It is straightforward to check that $C^{\star }$ is a chronicle function, that is, that the conditions (C1) and (C2) are satisfied.

We also need the following definition: Two chronicle functions C and D are said to differ at most at finitely many moments and their pasts if and only if

$$\begin{aligned} \exists n \exists t_{1}, ..., \exists t_{n} \forall u \, ((u \nleq t_{1} \wedge \cdots \wedge u \nleq t_{n}) \Rightarrow C(u) = D(u)). \end{aligned}$$

We let $\Delta _{P}^{{ fin}}(C)$ denote the set of chronicle functions which differ from C at most at finitely many moments and their pasts.

The lemma below gives a formal account of the reachability property discussed above.

Lemma 1

Let $(t,f) \in T^{\star }$ and $C \in \Delta _{P}^{{ fin}}(C^{\star })$ be given. For any $d \in {{\mathcal {C}}}(T,<)$ where $t \in d$ there exists a

$$\begin{aligned} D \in \Delta _{P}((t,f), C) \cap {{\mathcal {N}}}((t,f)) \end{aligned}$$

such that $\pi _{1}(D((t,f))) = d$.

Proof

By assumption C and $C^{\star }$ differ at most at finitely many moments and their pasts. So let $(u_{1},g_{1}), ...,(u_{n},g_{n}) \in T^{\star }$ be such that

$$\begin{aligned} \forall (v,h) \, ( ((v,h) \nleq ^{\star } (u_{1},g_{1}) \wedge \cdots \wedge (v,h) \nleq ^{\star } (u_{n},g_{n})) \Rightarrow C((v,h)) = C^{\star }((v,h))). \end{aligned}$$

For any $v \in T$, a set $K_{v}$ is defined as follows:

$$\begin{aligned} K_{v} = \{ (v,h) \in T^{\star } | \exists i \in \{1, ...,n \} \, ((v,h) \le ^{\star } (u_{i},g_{i})) \} \end{aligned}$$

Clearly, for any $v \in T$, the set $K_{v}$ is finite. Hence, for any $v \in T$, a natural number $r_{v}$ can be defined in the following way:

$$\begin{aligned} r_{v} = { sup}(\{ \pi _{2}(h(v))(v) | (v,h) \in K_{v} \}) +1 \end{aligned}$$

Here ${ sup}(\emptyset ) = 0$. Now, define $b \in {{\mathcal {C}}}(T^{\star },<^{\star })$ as follows:

$$\begin{aligned} b = \left\{ \left( w, x \mapsto \left\{ \begin{array}{ll} (d, z \mapsto r_{z}) &{} \text{ if } t < x \le w\\ f(x) &{} \text{ if } x \le t \end{array} \right. \right) | w \in d \right\} \end{aligned}$$

The wanted function $D:T^{\star } \rightarrow {{\mathcal {C}}}(T^{\star },<^{\star })$ can then be defined:

$$\begin{aligned} D((v,h)) = \left\{ \begin{array}{ll} b &{} \text{ if } (v,h) \le ^{\star } (t,f) \\ C((v,h)) &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

It has to be checked that D is a chronicle function, that is, that it satisfies the conditions (C1) and (C2). Clearly, (C1) is satisfied.

To check that (C2) is satisfied, assume that $(v',h') <^{\star } (v,h)$ and $(v,h) \in D((v',h'))$. We will show that $D((v',h')) = D((v,h))$. We just consider the only non-trivial case which is where $(v',h') \le ^{\star } (t,f)$ and $(t,f) <^{\star } (v,h)$, thus $D((v',h')) = b$ and therefore $(v,h) \in b$. We will then show that $D((v,h)) = b$. We first note that $D((v,h)) = C((v,h))$ since $(t,f) <^{\star } (v,h)$, cf. the definition of D. Now, it follows from $(v,h) \in b$ and $(t,f) <^{\star } (v,h)$, and hence $t < v$, that $(v,h) \notin K_{v}$ because

$$\begin{aligned} \pi _{2}(h(v))(v) = r_{v} > \pi _{2}(k(v))(v) \end{aligned}$$

for any $(v,k) \in K_{v}$. Hence $C((v,h)) = C^{\star }((v,h))$. But by the definition of the $C^{\star }$ function

$$\begin{aligned} C^{\star }((v,h)) = \left\{ \left( w, x \mapsto \left\{ \begin{array}{ll} (\pi _{1}(h(v)), z \mapsto \pi _{2}(h(v))(z)) &{} \text{ if } v < x \le w\\ h(x) &{} \text{ if } x \le v \end{array} \right. \right) | w \in \pi _{1}(h(v)) \right\} \end{aligned}$$

where

$$\begin{aligned} h(x) = \left\{ \begin{array}{ll} (d, z \mapsto r_{z}) &{} \text{ if } t<x \le v\\ f(x) &{} \text{ if } x \le t \end{array} \right. \end{aligned}$$

by $(v,h) \in b$ and the definition of b. Since $t < v$, it is the case that $\pi _{1}(h(v))=b$, and therefore $C^{\star }((v,h)) = b$. Hence $D((v,h)) = b$. So we conclude that (C2) is satisfied.

Clearly, D and C differ at most at (t, f) and its past. Furthermore, D is obviously normal at (t, f). Finally, $\pi _{1}(D((t,f))) = \pi _{1}(b) = d$. $\square$

Using the lemma above, we can prove the following theorem.

Theorem 2

Let a formula $\phi$ be given. For any $(t,f) \in T^{\star }$ and

$$\begin{aligned} C \in \Delta _{P}^{{ fin}}(C^{\star }) \cap {{\mathcal {N}}}((t,f)) \end{aligned}$$

it is the case that $V^{\star }((t,f),C,\phi )$ if and only if $V_{{ \! Ock}}(t,\pi _{1}(C((t,f))),\phi )$.

Proof

Induction on the structure of $\phi$. We proceed on a case by case basis.

• In the case where $\phi$ is a propositional letter q we have $V^{\star }((t,f),C,q)$ if and only if V(t, q) if and only if $V_{{ \! Ock}}(t,\pi _{1}(C((t,f))),q)$.

• The $\wedge$ case is straightforward.

• Also the $\lnot$ case is straightforward.

• The P case. By definition of the semantics $V^{\star }((t,f),C,P\psi )$ is equivalent to $V^{\star }((u,g),C,\psi )$ being the case for some $(u,g) <^{\star } (t,f)$. The induction hypothesis implies that this is equivalent to $V_{{ \! Ock}}(u,\pi _{1}(C((t,f))),\psi )$ being the case for some $u < t$. But this is equivalent to $V_{{ \! Ock}}(t,\pi _{1}(C((t,f))),P\psi )$ by definition of the semantics.

• The F case. By definition of the semantics $V^{\star }((t,f),C,F\psi )$ is equivalent to $V^{\star }((u,g),C,\psi )$ being the case for some $(u,g) \in C((t,f))$ such that $(t,f) <^{\star } (u,g)$. The induction hypothesis implies that this is equivalent to $V_{{ \! Ock}}(u,\pi _{1}(C((t,f))),\psi )$ being the case for some $u \in \pi _{1}(C((t,f)))$ such that $t < u$. But this is equivalent to $V_{{ \! Ock}}(t,\pi _{1}(C((t,f))),F\psi )$ by definition of the semantics.

• The $\square$ case. By definition of the semantics $V^{\star }((t,f),C,\square \psi )$ is equivalent to $V^{\star }((t,f),D,\psi )$ being the case for any

  $$\begin{aligned} D \in \Delta _{P}((t,f),C) \cap {{\mathcal {N}}}((t,f)). \end{aligned}$$

  It follows from the induction hypothesis and Lemma 1 that this is equivalent to $V_{{ \! Ock}}(t,d,\psi )$ being the case for any $d \in {{\mathcal {C}}}(T,<)$ where $t \in d$. But this is equivalent to $V_{{ \! Ock}}(t,\pi _{1}(C((t,f))),\square \psi )$ by definition of the semantics.

$\square$

The theorem above enables us to conclude that formulas validated by the alternative Braüner et al. (1998)-semantics are also validated by the Priorean Ockhamistic semantics.

Corollary 3

If a formula is Braüner et al. (1998)-valid, then it is also Ockhamist-valid.

Proof

For any $t \in T$ and $c \in {{\mathcal {C}}}(T,<)$ where $t \in c$, define $t ^{\star } \in T^{\star }$ as follows:

$$\begin{aligned} t ^{\star } = (t, x \mapsto (c, z \mapsto 1)). \end{aligned}$$

It is straightforward to check that $C^{\star }$ is normal at $t ^{\star }$. So it follows from Theorem 2 that $V^{\star }(t^{\star },C^{\star },\psi )$ is equivalent to $V(t,\pi _{1}(C^{\star }(t^{\star })),\psi )$ for any formula $\psi$. Note that $\pi _{1}(C^{\star }(t^{\star }))=c$. $\square$

6 Further work

We note that the whole battle described in the introduction of the present paper has been phrased in the terminology of model-theory. Of course, model-theory is a main branch of logic, but there is another branch, proof-theory, and whereas logical formulas in model-theory are interpreted in terms of models (a tradition going back to Tarski, at least), proof-theory is basically syntactic, but attempts to locate the meaning of a connective in the role it plays in logical rules (sometimes associated with Wittgenstein’s language games).⁹ Now, to the best knowledge of the present author, the issues at stake here have not been discussed in the terminology of proof-theory. And with the different philosophical baggage of proof-theory, this is not just an “innocent” shift of terminology, that is, speaking about the same thing in different terms, one reason being that proof-theory is often focused on constructive/intuitionistic reasoning, rather than the classical logic reasoning usually employed to reason about models in model theory.¹⁰ Our point here is that it could be interesting to investigate whether proof-theory could bring new aspects to the battle, which seems to have developed into a trench war with only relatively small changes in the frontline.

Another possible line of work is prompted by the observation that the logics considered in this battle can be seen as the combination of tense logics (the past and future tense operators P and F) with modal logics (the modal operator $\square$ for historical necessity). From a mathematical point of view, the logics under consideration have been developed, or generated, in a somewhat ad hoc way, determined by an exchange of arguments in philosophical discussions, but could not these logics have been generated in a more mathematically systematic (“natural”) way by using standard methods for combining logics, like the many ways to combine Kripke-style possible worlds models (fusion, product, fibring, dovetailing,...) described in Gabbay (1999) and elsewhere?

Appendix: An equivalence result

In this Appendix we give a clarified and detailed version of a proof originally given in Braüner et al. (1998), saying that the Priorean notion of Ockhamistic validity is equivalent to the version of Thomason and Gupta’s notion of validity we considered in Sect. 3. As alluded to in Sect. 3, this is so because true futures of counterfactual moments do not matter in the semantics given in that section. In that semantics, $\square \phi$ says that $\phi$ holds no matter how things will be, where “things” do not only refer to the true future of the present moment but also to true futures of future moments. Thus, even if a model does provide true futures of counterfactual moments, these futures do not matter if things will be different (and obviously not if things will be the same either).¹¹$^{,}$¹²

With the aim of proving the two notions of validity equivalent, we shall first prove a theorem which essentially says that chronicles can be “mimicked” by chronicle functions.

Theorem 4

Given a chronicle c there exists a chronicle function C such that for any moment $t \in c$ it is the case that $C(t)=c$.

Proof

In this proof we shall use Zermelo’s Theorem and Zorn’s Lemma which are both equivalent to the Axiom of Choice.¹³ Zermelo’s Theorem says that any set can be well-ordered, that is, it can be equipped with a linear partial order such that any non-empty subset has a least element. By Zermelo’s Theorem, we can assume that T is well-ordered by a relation $\sqsubseteq$. For any non-empty subset V of T we let $\sqcap V$ denote its $\sqsubseteq$-least element. Zorn’s Lemma says that if each linear subset of a non-empty partially ordered set A has an upper bound, then A has a maximal element. By Zorn’s Lemma, we can assume that for any moment t there exists a chronicle d such that $t \in d$, and hence, by the Axiom of Choice, we can assume that there exists a function

$$\begin{aligned} f:T \rightarrow {{\mathcal {C}}}(T,<) \end{aligned}$$

such that $t \in f(t)$ for any moment t. By transfinite induction using the relation $\sqsubseteq$, we define a function

$$\begin{aligned} C:T \rightarrow {{\mathcal {C}}}(T,<) \end{aligned}$$

such that

$$\begin{aligned} \begin{array}{c} C(t) = \left\{ \begin{array}{ll} c &{} \text{ if } t \in c \\ C(\sqcap \{ u \sqsubset t | t \in C(u) \}) &{} \text{ if } \exists u \sqsubset t \, (t \in C(u)) \\ f(t) &{} \text{ otherwise } \end{array} \right. \end{array} \end{aligned}$$

for any moment t. We only have to check that C satisfies the conditions (C1) and (C2). Clearly, (C1) is satisfied. Assume that $t<u$ and $u \in C(t)$. We then have to prove that $C(t)=C(u)$. It is straightforward to check that $t \in c$ if and only if $u \in c$, so without loss of generality we can assume that $t \notin c$ and $u \notin c$. Let $t_{0}=\sqcap \{ v | t \in C(v) \}$. Thus, $t_{0}$ is the $\sqsubseteq$-least moment where t belongs to the assigned chronicle. Hence, $t \in C(t_{0})$ and $t_{0} \sqsubseteq t$, and furthermore, $C(t_{0})=C(t)$. Now, $u \in C(t_{0})$ as $u \in C(t)$ so $u_{0} \sqsubseteq t_{0}$ where $u_{0}=\sqcap \{ w | u \in C(w) \}$. Thus, $u_{0} \sqsubseteq u$ and $C(u_{0})=C(u)$. But $t<u$ so $t \in C(u_{0})$ and hence $t_{0} \sqsubseteq u_{0}$ by definition of $t_{0}$. We conclude that $t_{0} = u_{0}$ so $C(t)=C(u)$. $\square$

The theorem above gives rise to an important corollary.

Corollary 5

Let a chronicle function C be given. For any chronicle c and moment $t \in c$ there exists a chronicle function $C'$ normal at t such that $C'(t)=c$ and $C' \in \Delta _{P,F}(t,C)$.

Proof

Let $K=\{ u | u \ne t \wedge u \nless t \wedge t \nless u\}$ and note that $T \setminus K$ is itself a frame, that is, irreflexive, transitive and backwards linear. We have $c \cap K = \emptyset$ because $t \in c$, so the preceding theorem can be applied to c considered as a chronicle in $T \setminus K$ to obtain a chronicle function $C'$ as appropriate. Note that any chronicle in $T \setminus K$ is also a chronicle in T. Furthermore, note that $T \setminus K$ is forwards closed. $\square$

The lemma we shall prove now essentially says that given a chronicle function, the semantics does not take into account true futures of counterfactual moments.

Lemma 6

Let a moment t be given. Let a formula $\phi$ be given. For any chronicle functions C and $C'$ normal at t such that $C(t)=C'(t)$, it is the case that $V(t,C,\phi )$ if and only if $V(t,C',\phi )$.

Proof

Induction on the structure of $\phi$. The induction hypothesis says that for any subformula $\theta$ of $\phi$ and any chronicle functions D and $D'$ normal at t such that $D(t)=D'(t)$, it is the case that $V(t,D,\theta )$ if and only if $V(t,D',\theta )$. To avoid confusion with the variable names in the lemma, other variable names have been used in the formulation of the induction hypothesis.

We only check the $\square$ case; the other cases are straightforward. Assume that $V(t,C,\square \psi )$ holds. We want to show that $V(t,C',\square \psi )$ holds (the converse is symmetric). By definition of the semantics we have $V(t,C',\square \psi )$ if

$$\begin{aligned} \forall C'' \in {{\mathcal {N}}}(t) \cap \Delta _{P,F}(t,C')\, V(t,C'',\psi ). \end{aligned}$$

So let a $C'' \in {{\mathcal {N}}}(t) \cap \Delta _{P,F}(t,C')$ be given, we then want to show that $V(t,C'',\psi )$. Consider the chronicle $C''(t)$ and apply Corollary 5. We then get a

$$\begin{aligned} C''' \in {{\mathcal {N}}}(t) \cap \Delta _{P,F}(t,C) \end{aligned}$$

such that $C'''(t)=C''(t)$. But since $\psi$ is a subformula of $\square \psi$, and $C''(t)=C'''(t)$, it follows from the induction hypothesis that $V(t,C'',\psi )$ if and only if $V(t,C''',\psi )$, so now we want to show that $V(t,C''',\psi )$. By definition of the semantics we have $V(t,C,\square \psi )$ only if

$$\begin{aligned} \forall C'''' \in {{\mathcal {N}}}(t) \cap \Delta _{P,F}(t,C) \, V(t,C'''',\psi ). \end{aligned}$$

Finally, we instantiate $C''''$ to $C'''$ and get $V(t,C''',\psi )$, which is what we wanted to show. $\square$

An important consequence of the preceding results is the following lemma.

Lemma 7

Let a formula $\phi$ be given. For any chronicle c and moment $t \in c$, the existence of a chronicle function C normal at t such that $C(t)=c$ and $V(t,C,\phi )$ is equivalent to $V(t,C',\phi )$ being the case for any chronicle function $C'$ normal at t such that $C'(t)=c$.

Proof

If there exists a chronicle function C normal at t such that $C(t)=c$ and $V(t,C,\phi )$, then by Lemma 6, $V(t,C',\phi )$ for any chronicle function $C'$ normal at t such that $C'(t)=c$. Conversely, assume that $V(t,C',\phi )$ for any chronicle function $C'$ normal at t such that $C'(t)=c$. By Theorem 4 there exists a chronicle function C such that $C(t)=c$. By Corollary 5 we can assume that C is normal at t. By assumption $V(t,C,\phi )$, which proves the converse. $\square$

We now prove a theorem making clear how truth in the Priorean Ockhamistic semantics is related to truth in the new semantics.

Theorem 8

Let a formula $\phi$ be given. Also, let a chronicle c and a moment $t \in c$ be given. Then $V_{{ \! Ock}}(t,c,\phi )$ if and only if for any chronicle function C normal at t such that $C(t)=c$ it is the case that $V(t,C,\phi )$.

Proof

Induction on the structure of $\phi$, thus, the induction hypothesis says that the theorem holds for any subformula of $\phi$.

The case where $\phi$ is a propositional letter follows from Theorem 4 together with Corollary 5. The $\wedge$ case is straightforward. The $\lnot$ case follows immediately from Lemma 7. The P and F cases follow from Lemma 7.

The $\square$ case goes as follows: By definition of the semantics, $V_{{ \! Ock}}(t,c,\square \psi )$ is equivalent to $V_{{ \! Ock}}(t,c',\psi )$ being the case for any $c'$ such that $t \in c'$. By the induction hypothesis this is equivalent to $V(t,C',\psi )$ being the case for any $C'$ normal at t such that $C'(t)=c'$ where $c'$ is any chronicle such that $t \in c'$. This is equivalent to the statement (let us call it A) that

$V(t,C',\psi )$ is the case for any $C'$ normal at t.

We have to show that statement A is equivalent to the statement (which we call B) that

$V(t,C, \square \psi )$ is the case for any C normal at t such that $C(t)=c$.

Recall that by definition of the semantics, $V(t,C, \square \psi )$ is equivalent to $V(t,C'',\phi )$ for any $C'' \in {{\mathcal {N}}}(t) \cap \Delta _{P,F}(t,C)$. It is straightforward that statement A implies statement B. Conversely, assume statement B, and let a chronicle function $C'$ normal at t be given. According to Corollary 5, there exists a chronicle function $C'''$ normal at t such that $C'''(t)=c$ and $C''' \in \Delta _{P,F}(t,C')$ (and hence $C' \in \Delta _{P,F}(t,C''')$). It follows from statement B that $V(t,C''', \square \psi )$ is the case, which by definition of the semantics implies that $V(t,C',\phi )$, from which we conclude that statement A follows from statement B. $\square$

The theorem above enables us to conclude that the two notions of validity in question are equivalent.

Corollary 9

A formula is valid in Prior’s Ockhamist semantics if and only if the formula is valid in the version of Thomason and Gupta’s semantics considered in Sect. 3.

Proof

Straightforward by the preceding theorem together with Lemma 7. $\square$