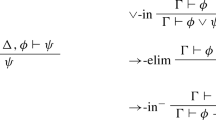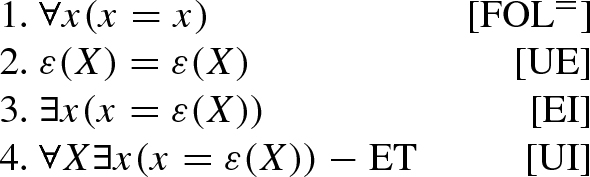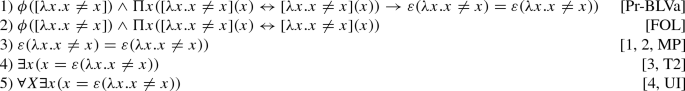Abstract
I present the traditional debate about the so called explanation of Russell’s paradox and propose a new way to solve the contradiction that arises in Frege’s system. I briefly examine two alternative explanatory proposals—the Predicativist explanation and the Cantorian one—presupposed by almost all the proposed solutions of Russell’s Paradox. From the discussion about these proposals a controversial conclusion emerges. Then, I examine some particular zig zag solutions and I propose a third explanation, presupposed by them, in which I emphasise the role of an implicit premise in the derivation of the paradox. In conclusion, I propose a different zig zag solution obtained by the adoption of a negative free logic.
Similar content being viewed by others
Notes
In the original Fregean presentation, the abstraction operator is a variable binding operator that applies to open formulas and binds an object variable in the formula to produce the name of an extension. However, for our present aim, we can consider—assuming the Fregean Rule of Substitution or a principle of \(\lambda \)-conversion—the abstraction operator as the described function symbol.
Where \(\phi (x)\) may be any formula not containing X free.
Or in a schematic version \(\varepsilon x.\phi x = \varepsilon x.\psi x \leftrightarrow \forall x (\phi x \leftrightarrow \psi x)\). In this paper, we will use the axiomatic one. However, as additions both to Frege’s original system and to our transliteration by full second-order logic (with impredicative comprehension axiom schema), the axiomatic version and the schematic one are equivalent. (The schematic version of BLV is stronger than the single quantified axiom only in the context of restricted and predicative second-order logic. Cfr. Heck 1996).
In the standard models, the first-order domain is a countable set and, according to the extensional consideration of the concepts, the second-order domain is the (uncountable) power set of the first-order domain.
I will formulate the criteria with regard to the explanations because they represent the explicit subject of such debate. However, considering the described link between the notions of explanation and solution of a paradox, it is understood that we will be able to verify that the explanations meet such criteria only by examining their corresponding solutions.
In a literal sense, none of the theories which will be examined could be considered logicist because they obtain a derivation of the arithmetic from a logical system augmented with a (non-logical) abstraction principle (a version of BLV)—and we know that it isn’t a purely logical result. On the contrary, Frege would have considered such result as a logicist achievement because he considered BLV as a logical axiom. Thus, since such sort of abstractionist theories remains the framework of this debate, in this paper, we will call “logicist”—in this broad and Fregean sense—any logical theory augmented with an abstraction principle which meets one of the Logicist conditions to be presented hereafter, namely which is able to recover Peano or Frege Arithmetic.
According to Antonelli and May (cfr. Antonelli and May 2005), a relevant part of Frege’s foundational idea is precisely his Extensionalist program, namely the reconstruction of arithmetic in terms of a theory of concepts extensions. We can anticipate that, instead, in the rest of the paper we will use such label, “Extensionalist”, to indicate only a special way, i.e. the adoption of a specific explanation and the solutions that it suggests, to recover such goal. We can say that the Extensionalist explanation and solutions which will be proposed will represent a new way to achieve the described Logicist conditions.
This was the original meaning of BLV. Cfr. (Frege 1903). Such requirement is betrayed by all the traditional solutions (Cantorian solutions presuppose more concepts than extensions, whereas Predicativist solutions prove the existence of more non-logical objects than concepts—cfr. Wehmeier 1999) and by most of the zig zag solutions (both the theory in Ferreira (2018) and the solutions which will be proposed with free logic presuppose more concepts than extensions). Such requirement is instead preserved in Boccuni (2010) by a formal and philosophical distinction between concepts and pluralities.
Cfr. (Payne 2013).
These features characterise Fregean style and represent further interesting achievements of any attempt of recovering the original Fregean program but are not essential to recapture of the logicist and extensionalist core of Fregean foundation of mathematics. It would be better to comply as far as possible with these criteria but—if this complete goal will result impossibile—we will consider the violation of these last requirements less severe than the failure of the others.
In what follows, we will consider, as more or less (hence partially) Fregean, a theory based on how many of this Fregean conditions are preserved by the explanation of Russell’s Paradox that such theory presupposes.
In a higher-order formulation, Cantor’s theorem is: \(\lnot \exists \iota \forall F \forall G (\iota (F) = \iota (G) \rightarrow \forall x (Fx \leftrightarrow Gx))\).
Cfr. (Heck 1996).
Cfr. (Paseau 2015).
Such definition consists in the negation of a predicative formula and it is enough to present the general version of the Predicativist thesis. More precisely, the Predicativist explanation should adopt a wider meaning of impredicativity which refers to all the instances of comprehension axiom schema containing bound second-order variables (in the scope of a quantifier) or bound first-order variables (in the scope of an abstraction operator. In this way, we can consider impredicative also an instance of \(\exists X\forall y (Xy \leftrightarrow \lnot \alpha (y)y)\), where \(\alpha \) is an abstraction operator which applies to first-order terms). Indeed, the comprehension formula (\(\lnot \alpha (y)y\)) only apparently lacks a bound second-order variable because it implicitly and indirectly presupposes the same (problematic—in a predicative perspective) value. This broad definition of impredicativity involves a feasible Predicativist answer—which I would endorse—to an objection raised in Uzquiano (2019).
Intended as the derivation of (any axiomatisation of) arithmetic from second-order logic. Cfr. note 6.
Intended as the conception and formalisation of arithmetic as a theory about the extensions of the concepts. Cfr. note 7.
On the contrary, both the mentioned systems share—even if for different reasons—a Predicativist explanation. In Ferreira (2018), Predicativist diagnosis is resumed in its Dummettian version; instead, in Boccuni (2010), Predicativist explanation is supported by a new reading of Russell’s Vicious Circle Principle as corollary of a thesis about the adoption of the arbitrary reference in mathematical and logical reasoning. For a discussion of VCP as presupposition of the quantification rules and of the arbitrary reference in mathematics, cfr. also (Boccuni 2015).
In the following paragraphs we also test such explanation by sketching—and then evaluating—a theory which represents its corresponding solution.
Derivation of the Extensions Theorem:
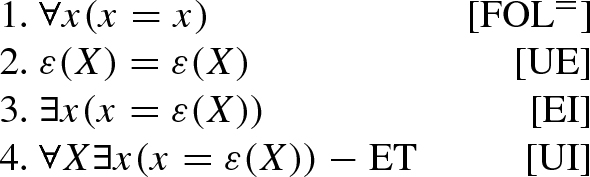
Cfr. (Ferreira 2018).
Cfr. (Boccuni 2010).
Cfr. (Boccuni 2011).
The existence of the abstracts is a consequence of the reflexivity of the abstraction relation (which is not necessarily an equivalence relation, cfr. Payne 2013):

If Russell’s concept is reflexively co-extensional with itself we derive that its extension exists and, from this result, the contradiction; but, if we refute the existence of Russell’s extension, Russell’s concept turns out to be reflexively co-extensional with itself and then, again, able to introduce its extension.
In this language there are denumerably many first-order variables, denumerably many second-order variables and a term-forming operator \(\varepsilon \) which, in the usual way, applies to monadic second-order variables to produce singular terms.
In this language, we can also define the universal form of both the “restricted” quantifier (\(\forall x Ax =_{def} \lnot \exists x \lnot Ax \)) and the “unrestricted” one (\(\Pi x Ax =_{def} \lnot \varSigma x \lnot Ax\)); additionally, we can usefully define a predicative monadic constant E!: E!a \(=_{def}\) \(\exists x (x = a)\).
Negative free logic axioms:
NF1) \(\forall v \alpha \rightarrow (E!t \rightarrow \alpha (t/v))\); NF2) \(\exists v E!v\); NF3) \( s=t \rightarrow (\alpha \rightarrow \alpha (t//s))\); NF4) \(\forall v (v=v)\); NF5) \(\Lambda \tau _1, \ldots , \tau _n \rightarrow E! \tau _i\) (with \(1\le i \le n\)), where \(\Lambda \) is any predicate.
Free logic quantification rules:
UI\(_{fl}\)): \(E!a \ldots \phi (a/x) \vdash \forall x \phi \); UE\(_{fl}\)): \(\forall x \phi , E!a \vdash \phi (a/x)\); EI\(_{fl}\)): \(\phi (a/x), E!a \vdash \exists x \phi \); EE\(_{fl}\)): \(\phi (a/x), E!a \ldots \psi , \exists x \phi \vdash \psi \), where a is a new individual constant which does not occur in \(\phi \) and \(\psi \).
We can note that second-order quantification and axioms rules are entirely analogue to the axioms and rules for restricted first-order quantification but they distinguish themselves from the analogue axioms and rules for un-restricted first-order quantification. Because of this, we are not able to state quantification axioms and rules in a unique version for both first- and second-order quantification.
CA) \(\exists X \Pi x (Xx \leftrightarrow \alpha )\).
From these axioms we can also derive, as theorems:
T1) \(\forall x E!x\);
T2) \(t = t \leftrightarrow E!t\);
T3) \((\lnot E!s \wedge \lnot E!t) \rightarrow (\alpha \rightarrow \alpha (t//s))\).
We probably need a third-order language to formulate, in the language of the theory, the condition expressed by the formula \(\phi \). In this debate, the restrictions are often expressed in the meta-language (e.g. predicative restriction of CA in Heck (1996), Wehmeier (1999), Ferreira and Wehmeier (2002), Boccuni (2010), Ferreira (2018) or other restrictions of BLV in Boolos (1987), Uzquiano (2019), Payne (2013)) and I propose a possible interpretation of the restrictive condition suggested in Payne (2013). However the main focus of this proposal concerns a possible weakening of the semantic commitment of first-order logic and this fact isn’t affected by whether we do adopt a second- or higher-order language.
Such remark was suggested to me by Marco Panza in a personal communication. It is needed in order to make the definition of the predicative condition acceptable to both sides of the debate about the syntactical complexity of the comprehension formulas. According to the “compositional” attitude, which I endorse, the syntactical evaluation of a comprehension formula presupposes the replacement of any predicate constant with the comprehension formula by which it is specified; then, the syntactical complexity of a comprehension formula and its predicative (or impredicative) condition result from the replacement of any predicate constants included in the formula with its own comprehension formula—in such case, the remark is only a parenthetical clarification. Contrarily, according to the “non-compositional” attitude, the possibility of replacing a predicate constant with its own comprehension formula does affect both the syntactical complexity and the predicative (or impredicative) condition of the formula which included such predicate—in this case, the remark is an essential integration of the restriction. I am very grateful to Marco Panza for drawing my attention to the difference between these two attitudes.
Cfr. note 42.
We will consider primitive a formula which contains only primitive symbols of our language L\(_F\) (\(\lnot , \wedge , \vee , =, \exists \))—i.e. \(\forall X \exists x(\lnot (\lnot Xx))\) is not primitive because its expression could be reduced to \(\exists X \exists x (\lnot Xx)\). For such reason, other formulas, logically equivalent to the Russellian formula (e.g. \(\lnot \forall X (\lnot (x= \varepsilon X \vee Xx))\)), are not positive because they could be reduced to \(\exists X(x= \varepsilon X \wedge \lnot (Xx))\).
For example, \(\exists X \exists x (\lnot Xx)\) is not positive; \(\exists X \exists x(Xx \wedge \lnot (x=x))\) is positive. It is evident that the Russellian formula (the formula which specifies Russell’s predicate), \(\exists X(x= \varepsilon X \wedge \lnot (Xx))\), is not positive. Cfr. (Halbach 2014; Liu 2012).
An important exception to such consideration is provided by the Extensionalist project of Antonelli and May in Antonelli and May (2005). In this system, an existential restriction is imposed on a weakened version of Basic Law V: \(\forall P \forall Q \forall x \forall y (VR(P, x) \wedge VR(P,y) \rightarrow \forall z_1, \ldots z_n(P, z_1, \ldots , z_n) \leftrightarrow z=Y)\), where VR(P, x) is a predicate with the intended interpretation that x is the value range of P (this version of BLV says that if concepts P and Q have value ranges, then their value ranges are identical precisely when P and Q are equi-extensional). But, in this project, the logicist part of Fregean program is explicitly given up and arithmetic is reconstructed like a “non-logical theory of extensions”. Then such version of BLV is purposely formulated in such a way as not to have existential import.
Cfr. (Frege 1903).
We can introduce, by given vocabulary, set-theoretic definitions of cardinal numbers (0 =\(_{def} \varepsilon (\lambda x. x \ne x)\); 1 =\(_{def}\varepsilon (\lambda x. x = 0)\); ...) and prove the existence of each of them. For example:
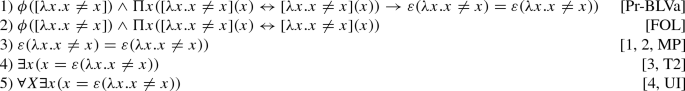
Then, we can provide a predicative or set-theoretic definition of the arithmetical notions as Predicative Singleton or Successor (\(S_p \equiv _{def}\varepsilon (\lambda x. x = n)\)), Predicative Inductive property (\(I(X)_p \equiv _{def} X0 \wedge \forall z (Xz \rightarrow X\varepsilon (\lambda x. x = z))\)) and Predicative Natural Number (\(\mathbb {N}_p x \equiv _{def} \forall X(I(X) \rightarrow Xx)\)).
Given the previous definitions, we can derive a formulation of second-order Peano Arithmetic analogue to that in Boccuni (2010). Cfr. “Appendix A”.
The cost of such results is giving up some of the additional Fregean conditions, like the full injectivity of the extensionality function—more precisely, the behaviour of the function is injective with respect to the proper subset of the second-order domain involving only positive concepts.
We can note that, by defining cardinal numbers in terms of extensions of the concepts, the warranty of their denotation lies in the syntactical form of such extensional terms: cardinal terms are non-empty terms only if their extensional transliteration is positive (namely fits the Ps-BLV’s requirements).
We can observe that such definition of the number zero in terms of a positive extension, meeting the restriction on the right-side of Ps-BLV, guarantees that this term have a denotation—namely that we are able to prove, by Ps-BLV, that the number zero exists. The existence of zero, in turn, grants the existence of the other cardinal numbers, according to their Fregean (positive) definition: each number a, different from zero, is definable as the extension of the concept \([\lambda x. \exists X (x = \varepsilon (X) \wedge X \approx [\lambda x. x = a])]\), whose comprehension formula—in general, first-order identity with a non-empty term—necessarily results to be positive, i.e. 1 =\(_{def}\) \(\sharp ([\lambda x. x = 0])\) = \(\varepsilon (\lambda x. \exists X (x = \varepsilon (X) \wedge X \approx [\lambda x. x = 0]\))), etc....
From now on, the condition \(\phi \) means positive.
Cfr. note 51.
The proof of the existence of the extensions (and then of the cardinals) from the right-to-left conditional involved in BLV (or HP) is a quick standard derivation which proceeds in analogue way in every Fregean (and Neo-Fregean theory). Cfr. note 48.
Cfr. note 48. In this Appendix (A) the condition \(\phi \) means predicative.
Cfr. par. 5.1. In this Appendix (B), the condition \(\phi \) means positive.
For a detailed proof, cfr. (Zalta 2010).
References
Antonelli, A., & May, R. (2005). Frege’s other program. Notre Dame Journal of Formal Logic, 46(1), 1–17.
Boccuni, F. (2010). Plural Grundgesetze. Studia Logica, 96(2), 315–330.
Boccuni, F. (2011). On the consistency of a plural theory of Frege’s Grundgesetze. Studia Logica, 97(3), 329–345.
Boccuni, F. (2015). Frege’s Grundgesetze and a reassessment of predicativity. From logic to practice (pp. 53–70). Cham: Springer.
Boolos, G. (1987). Saving frege from contradiction. Proceedings of Aristotelian Society, 87, 137–151.
Cocchiarella, N. B. (1992). Cantor’s power-set theorem versus Frege’s double correlation thesis. History and Philosophy of Logic, 13, 179–201.
Dummett, M. (1991). Frege, philosophy of mathematics. Oxford: Oxford University Press.
Dummett, M. (1994). Chairman’s address: Basic law V. In Proceedings of the Aristotelian Society (Vol. 94, pp. 243–251). Aristotelian Society, Wiley.
Ferreira, F. (2018). Zigzag and Fregean arithmetic. In H. Tahiri (ed.), The philosophers and mathematics (Vol 43, pp. 81–100). Springer International
Ferreira, F., & Wehmeier, K. F. (2002). On the consistency of the \(\Delta _1^1\)-CA fragment of Frege’s Grundgesetze. Journal of Philosophical Logic, 31, 301–311.
Frege, G. (1903). Grundgesetze der Arithmetik (Vol. II). Jena: Verlag Hermann Pohle.
Halbach, V. (2014). Axiomatic theories of truth. Cambridge: Cambridge University Press.
Heck, R. K. (1996). The consistency of predicative fragments of Frege’s Grundgesetze der Arithmetik. History and Philosophy of Logic, 17, 209–220.
Liu, J. (2012). Second-order positive comprehension and Frege’s basic law V. Frontiers of Philosophy in China, 7(3), 367–377.
Paseau, A. C. (2015). Did Frege commit a Cardinal Sin? Analysis, 75(3), 379–386.
Payne, J. (2013). Abstraction relations need not be reflexive. Thought, 2, 137–147.
Quine, W. V. (1955). On Frege’s way out. Mind, 64, 145–159.
Russell, B. (1903). On some difficulties in the theory of transfinite numbers and order types. In Russell, B. (1973). Essays in Analysis, New York.
Sainsbury, R. M. (2009). Paradoxes. Cambridge: Cambridge University Press.
Shapiro, S. (2000). Prolegomenon to any future neo-logicist set theory: Abstraction and indefinite extensibility. The British Journal for the Philosophy of Science, 54, 59–91.
Uzquiano, G. (2019). Impredicativity and paradox. Thought: A Journal of Philosophy, 8(3), 209–221.
Wehmeier, K. F. (1999). Consistent fragments of Grundgesetze and the existence of non-logical objects. Synthese, 121(3), 309–328.
Zalta, E. N. (2010). Frege’s logic, theorem, and foundations for arithmetic. Stanford Encyclopedia of Philosophy.
Acknowledgements
An earlier version of this paper was presented at the 4th SILFS Postgraduate Conference on Logic and Philosophy of Science at the University of Urbino, 3–7 June 2019. I wish to thank Pierluigi Graziani and all the other organisers. I wish also to thank the participants that, in such venue, gave me their feedback. This article develops a chapter of my Phd dissertation and I would take this opportunity to thank my supervisors—Francesca Boccuni, whose works and words inspired my interest in philosophy of mathematics, and Tommaso Piazza, whose teachings deeply influenced my philosophical growth. I am very grateful to them also for their assistance in drawing up this article: much of it is due to invaluable discussions with Francesca Boccuni and very helpful advice of Tommaso Piazza. I wish also to thank Andrea Sereni and Salvatore Florio, whose remarks on my dissertation have been very useful in writing this paper. I would express a special thank to Marco Panza, for illuminating discussions and decisive suggestions. Finally, I wish to thank two anonymous referees, whose comments greatly helped me to improve the final version of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Given Pr-BLV and provided the set-theoretic definitions of the arithmetical notions,Footnote 58 we can derive the axioms of Peano Arithmetic.
Theorem 7
(PA1) \(\mathbb {N}_p0\).
Proof

\(\square \)
Theorem 8
(PA2) \(\forall x (S_px \ne 0)\).
Proof

\(\square \)
Theorem 9
(PA3) \(\forall y \forall z (\varepsilon ([\lambda x. x = y]) = \varepsilon ([\lambda x. x = z]) \rightarrow y = z)\).
Proof

\(\square \)
Theorem 10
(PA4) \(\forall X (X0 \wedge \forall y (Xy \rightarrow X\varepsilon (\lambda x. x=y)) \rightarrow \forall x (Xx))\).
Proof
It follows from the definition of \(\mathbb {N}_p\). \(\square \)
Theorem 11
(PA5) \(\forall y \exists x (x = \varepsilon ([\lambda x. x =y]))\).
Proof

\(\square \)
Appendix B
Given Ps-BLV and provided the Fregean definitions of the arithmetical notions,Footnote 59 we can sketch the structure of Frege’s Theorem in Ps-FL.
Lemma 8
(Reflexivity of weak ancestor) \(\forall x P'' (xx)\).
Proof

\(\square \)
Lemma 9
(Lemma about Zero) \(\forall X (\sharp (X) = 0 \leftrightarrow \lnot \exists x (Xx))\).
Proof

\(\square \)
Theorem 12
(PA1) \(\mathbb {N}\)0.
Proof

\(\square \)
Theorem 13
(PA2) \(\lnot \exists x (\mathbb {N}x \wedge P(x,0))\).
Proof

\(\square \)
Lemma 10
(Lemma about equinumerosity): \(F \approx G \wedge Fx \wedge Gy \rightarrow [\lambda z. Fz \wedge z \ne x] \approx [\lambda z.Gz \wedge z\ne y]\).
Theorem 14
(PA3) \(\forall x \forall y \forall z (P(xz) \wedge P(yz) \rightarrow x =y)\).
Proof

\(\square \)
Definition 10
\(E_P(F) \equiv _{def} \forall x\forall y(P(xy) \rightarrow (Fx \rightarrow Fy))\).
Definition 11
\(E_{R''_a}(F) \equiv _{def} \forall x\forall y(R''(ax) \wedge R''(ay) \rightarrow (Fx\rightarrow Fy))\).
Theorem 15
(General Inductive Principle): \(\forall x(Fx \wedge E_{R''_x}(F)\rightarrow \forall y (R''(xy) \rightarrow Fy))\).Footnote 60
Theorem 16
(PA4) \(F0 \wedge E_{\mathbb {N}}(F\mathbb {N}) \rightarrow \forall x Fx\).
Proof
It follows, as an instance, from Theorem 15. \(\square \)
Lemma 11
(Lemma about Successors) \(\forall x (\mathbb {N}x \rightarrow P(x \sharp ([\lambda z. P''(zx)])))\).
Corollary 1
\(\forall R (R''(xy) \wedge R(yz) \rightarrow R^*(xz))\).
Corollary 2
\(\forall R (R^*(xy) \rightarrow R''(xy))\).
Lemma 12
(Lemma about Natural Numbers) \(\forall x \forall y (\mathbb {N}x \rightarrow (P(xy) \rightarrow \mathbb {N}y))\).
Proof

\(\square \)
Theorem 17
(PA5) \(\forall x (Nx \rightarrow \exists y (Ny \wedge P(xy)))\).
Proof
Rights and permissions
About this article
Cite this article
Conti, L. Russell’s Paradox and Free Zig Zag Solutions. Found Sci 28, 185–203 (2023). https://doi.org/10.1007/s10699-020-09689-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10699-020-09689-7