Abstract
This article explores the changing relationships between geometric and arithmetic ideas in medieval Europe mathematics, as reflected via the propositions of Book II of Euclid’s Elements. Of particular interest is the way in which some medieval treatises organically incorporated into the body of arithmetic results that were formulated in Book II and originally conceived in a purely geometric context. Eventually, in the Campanus version of the Elements these results were reincorporated into the arithmetic books of the Euclidean treatise. Thus, while most of the Latin versions of the Elements had duly preserved the purely geometric spirit of Euclid’s original, the specific text that played the most prominent role in the initial passage of the Elements from manuscript to print—i.e., Campanus’ version—followed a different approach. On the one hand, Book II itself continued to appear there as a purely geometric text. On the other hand, the first ten results of Book II could now be seen also as possibly translatable into arithmetic, and in many cases even as inseparably associated with their arithmetic representation.
Similar content being viewed by others
Notes
Beginning in the late nineteenth century, this view was promoted by prominent scholars such as Paul Tannery (1843–1904), Hieronymus Georg Zeuthen (1839–1930), Sir Thomas Little Heath (1861–1940), and Otto Neugebauer (1899–1990). Book II became a pivotal focus in the elaboration of the details of this historiographical perspective.
The issue of the adequate use of direct and indirect sources in order to establish an authoritative version of the Euclidean text is a significant historiographical question still under debate nowadays. See (Rommevaux et al. 2001). I do not deal at all with this issue here, and I simply follow the widely accepted English version (Heath 1956 [1908]).
Recent scholarship has devoted increased attention to the ways in which diagrams appearing in critical editions of the Elements differ from those in extant manuscripts. See, e.g., (Saito and Sidoli 2012). Although considerations of this kind may be relevant to our analysis here, in this article I will refer only to diagrams as they appear in the available critical editions.
The distinction between the two kinds of proofs has efficiently been used in (Oaks 2011) for the case of Islam mathematics.
See Doron Zeilberger, Opinion 82: “A Good Lemma is Worth a Thousand Theorems” (written: August 14, 2007; downloaded May 02, 2012: http://www.math.rutgers.edu/~zeilberg/Opinion82.html): “Theorems are nice, but they are usually dead-ends. A lemma may be ‘trivial’, or easy to prove once stated, but if it is good, its value far surpasses even the deepest theorems.”
And for an English translation, see (Lo Bello 2009, 32).
(Vitrac 2005, 6 ff.) speaks about two contrasting styles of geometrical proof in Greek mathematics: “demonstrative” versus “algorithmic.” Without wanting to make too much of word choice, and without the benefit of the much broader scope of Vitrac’s analysis, I think that for the case of Book II, at least, the contraposition of “constructive” versus “operational” is more adequate to encapsulate the difference between Euclid’s and Heron’s proofs.
A Latin version is extant which dates from the fourteenth century (Sesiano 1993). I will be referring to this Latin text, which most likely reflects what was available to the European mathematicians we shall be discussing below. There is also a Hebrew version with comments by Mordechai Finzi (died 1475) which seems to have been a translation from a Spanish version, but no such Spanish version has been preserved. See (Levey 1966; Weinberg 1935).
See also Oaks 2011, 255–256.
“... sicut dixit Euclides in secundo tractatu libri sui”.
Besides this method of solution for finding the thing, whose validity is proved in two different ways, Abū Kāmil also introduced a second method of solution directly yielding the value of the square. Although highly interesting in itself, it is beyond the scope of the present article. See (Sesiano 1993, 329–330; Moyon 2007, 310).
This text in its various extant manuscripts and translations has had a somewhat convoluted history (Brentjes 2001b), which I will not delve into here. I will refer to the text as rediscovered and published in Latin translation in (Curtze 1899). For details, see also (Lo Bello 2003a, 2009; Tummers 1994).
In Curtze’s late-nineteenth-century edition of this text, Al-Nayrīzī’s commentary was accompanied by a footnote in which he formulated the original Euclidean text together with an algebraic rendering of the proposition (Curtze 1899, 94). Even here this algebraic rendering is anachronistic. Reinterpreting a geometric result in arithmetic terms (as Al-Nayrīzī did) is not yet the same as reinterpreting it algebraically.
Neither Curtze nor—to the best of my knowledge—any other later commentator has called attention to the remarkable fact that al-Nayrīzī’s IX.16 is an addition to, and indeed a generalization of, Euclid’s IX.15, and that, incidentally, an interesting feature of Euclid’s proof of IX.15 is its reliance on what seem to be arithmetic versions of II.3 and II.4 (Heath 1956 [1908]), Vol. 2, 404–405). Campanus, following al-Nayrīzī, included arithmetic versions of propositions of Book II as additions to the same IX.16. I discuss this point in greater detail in [LC2].
One interesting point of his Latin version is that in Al-Nayrīzī’s additions to IX.16, products of numbers are called “areas” (superficiales).
The introduction to (Busard 2005) contains a clear and well-organized summary of the rich and scholarly impressive literature that has dealt over the last thirty years with the issue of the Latin versions of the Elements. The reader may also consult the following: (Brentjes 1997/1998, 2001a); (Busard 1983, 1984, 1996a; Busard and Folkerts 1992; Folkerts 2006—Section III); (Murdoch 1968, 1971).
Unless otherwise stated, translations from Latin, Hebrew, or German are mine.
The Hebrew printed version of Bar Ḥiyya’s text is accompanied by an introduction in Hebrew written by Guttmann, and it contains further comments, also in Hebrew, written by Zvi Hirsch Yaffe (1853–1927). The Guttmann edition also served as the basis for a translation of the text to Catalán (Millás-Vallicrosa 1931).
The paragraphs are numerated in the edition I am using here. I add the initials BH, for ease of reference.
Read from the point of view of current Hebrew usage, Bar Ḥiyya’s terminology may give rise to some confusion, as was pointed out in (Sarfatti 1968, 82). I am following here Sarfatti’s interpretation (e.g., multiplication for “
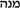
”, addition for “
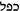
”, root for “
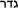
”). For a brief account of the differences between ancient and modern Hebrew mathematical terminology, see (Corry and Schappacher 2010, 449–457).
Actually, the text in Guttmann (1912–1913), p. 15, says: “
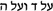
” (on 4 and on 5). But this seems to be a typo.
(Guttmann 1912–1913, 15) [In the quotation, I have replaced the Hebrew letters appearing in the original diagram with the letters I am using here in my diagram]:
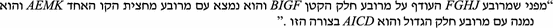
These include, in the order in which they appear, versions of: III.35, I.33, VI.4, I.37, I.38, I.41, I.35, I.36, and VI.1.
In Sect. 49: “
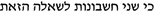
”. In the text Bar Ḥiyya sometimes calls the number by its name and sometimes uses the alphabetic characters ...
to indicate them. For the side of the square or for the unknown Bar Ḥiyya uses alternatively
and
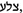
even within the same sentence. The text has many interesting linguistic aspects that I do not discuss here, starting with the very use of the word “thisboreth” (
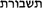
).
Like with the Hebrew text, also here there are some open issues concerning the manuscripts. See (Curtze 1902, 4).
A detailed analysis of this problem and its roots in Babylonian mathematics appears in (Sesiano 1987).
It would also be of particular interest to compare Fibonacci’s proof of II.5 with all the others discussed here, but in consideration with the length of this article I will focus on II.9 alone.
(Høyrup 2010, 16) has argued that the potential impact of the Arithmetica materialized only to a very limited extent. Here I want to focus on the way in which, via its reading by Campanus, it did have an important influence in the specific issue of the increasingly arithmetic-algebraic conceptions of Book II.
The Stapulensis printed version of 1496 does include numerical examples. In this as well as in other respects, it is interesting to compare the printed with the original Jordanus’ version. We shall leave this comparison for a future opportunity.
It must be stressed, however, that Jordanus included in his treatise another proposition, A-X.3, which is in fact equivalent to A-I.19 and that embodies the so-called Regula Nicomachi: given three numbers in arithmetic progression, \(a-b=b-c\), then we have \(b^{2}-a\cdot c = (a-b)^{2}\). Boethius has stated in his Arithmetica that this rule was discovered by Nicomachus (Busard 1991, 14). Jordanus’ very short proof of A-X.3 simply invokes A-I.19. This apparent repetition reflects, so it seems to me, Jordanus’ conscious view of A-I.19 as naturally belonging to the context of this preliminary type of results, where a given number is separated in two parts and the relations between the partial products, even if an equivalent form of it could appear in the context of a later book as well.
It is pertinent to refer the reader in this regard to (Puig 1994). This seldom-cited, but highly original article makes a remarkable connection between the arithmetic results presented in Jordanus’ De numeris Datis and the diagrammatic aspects underlying the arguments of the proofs. I discuss this in some detail in [LC2].
See also Campanus’ comments to VII.6 (p. 236), which is compared with V.13 (i.e., Euclid V.12).
All of these are very interesting in themselves, but discussing them would be beyond the scope of this article. See (Rommevaux 1999, 93–100).
The only other place where we find such additions to the diagram is in the very last arithmetic proposition, IX.39.
These are comments 4–12. Comments 1–3 correspond to Jordanus’ A-I.9–A-I.11, whereas comment 13 corresponds to Euclid’s V.11. See (Busard 2005, 33).
The difference is directly noticeable by comparing steps (l.1)–(l.5) here below with steps (c.1)–(c.7) for Heron, with (k.1)–(k.5) for Jordanus, or with the algebraic interpretation that (Curtze 1899, 96) provides in a footnote for Al-Nayrīzī.
Though I would not like to lay excessive stress on names, I feel it is improper to claim, as in (Busard 2005, 39), that “the algebraic method which Campanus used for proving Campanus IX.16 add. 4–12 agrees with the method which Anairitius used for proving II.2–II.10.” For one thing, I already indicated that both the “method” and the line of argumentation actually differ from that of Al-Nayrīzī. But also, using the term “algebra” in this context may be misleading since nothing here is manipulation of abstract symbols according to formal rules, not even in the manner intended in Islamic mathematics. Rather, Campanus simply operates on numbers (which are indicated with letters that serve as names) according to general, arithmetic rules.
Here, I refer to the text as is appears in (Lange 1909), which is where the Hebrew text first appeared in print in modern times, together with a German translation. See also (Simonson 2000a, b) for a description of the contents, for some important remarks concerning the existing manuscripts and versions, and for additional parts not appearing in the Lange edition.
The full original Greek text appears in (Heiberg and Menge 1883–1893, Vol. 5), as Appendix Scholiorum 4. I thank Michael Fried for help on translating parts of it.
References
Archibald, Raymond C. 1913. Euclid’s book on divisions of figures with a restoration based on the Woepcke’s text and on the practica geometriae of Leonardo Pisano. Cambridge: The University Press.
Billingsley, Henry. 1570. The elements of geometrie of the most auncient philosopher Euclide of Megara. London. Imprinted by Iohn Daye.
Brentjes, Sonja. 1994. Textzeugen und Hypothesen zum arabischen Euklid in der Überlieferung von al-Ḥağğāğ b. Yūsuf b. Maṭar (zwischen 786 und 833). Archive for History of Exact Sciences 47: 53–92.
Brentjes, Sonja. 1996. The relevance of non-primary sources for the recovery of the primary transmission of Euclid’s Elements into Arabic. In Tradition, transmission, transformation: Proceedings of two conferences on pre-modern science held at the university of Oklahoma, ed. F. Jamil Ragep, Sally P. Ragep, and Steve Livesey, 201–225. Brill: Leiden.
Brentjes, Sonja. 1997/1998. Additions to Book I in the Arabic traditions of Euclid’s Elements. Studies in History of Medicine and Science 15(1–2): 55–117.
Brentjes, Sonja. 2001a. Observations on Hermann of Carinthia’s version of the Elements and its relation to the Arabic transmission. Science in Context 14(1–2): 39–84.
Brentjes, Sonja. 2001b. Two comments on Euclid’s Elements? On the relation between the Arabic text attributed to al-Nayrızı and the Latin text ascribed to Anaritius. Centaurus 43: 17–55.
Busard, Hubertus L.L. 1968. The translation of the Elements of Euclid from the Arabic into Latin by Hermann of Carinthia (?). Edited with an Introduction. Leiden: Brill.
Busard, Hubertus L.L. 1983. The first Latin translation of Euclid’s ‘Elements’, commonly ascribed to Adelard of Bath. Toronto: Pontifical Institute of Medieval Studies.
Busard, Hubertus L.L. 1984. The Latin translation of the Arabic version of Euclid’s ‘Elements’, commonly ascribed to Gerard of Cremona. Leiden: Brill.
Busard, Hubertus L.L. 1987. The medieval Latin translation of Euclid’s Elements made directly from the Greek. Stuttgart: Steiner Verlag.
Busard, Hubertus L.L. 1991. Jordanus de Nemore, De elementis arithmetice artis: A medieval treatise on number theory, 2 vols. Stuttgart: Franz Steiner Verlag.
Busard, Hubertus L.L. 1992. The Arithmetica of Jordanus Nemorarius. In Amphora: Festschrift for Hans Wussing on the occasion of his 65th birthday, ed. S.S. Demidov, et al., 121–132. Basel-Boston-Berlin: Birkhäuser Verlag.
Busard, Hubertus L.L. 1996a. A thirteenth-century adaptation of Robert of Chester’s version of Euclid’s Elements. Munchen: Institut fur Geschichte der Naturwissenschaften.
Busard, Hubertus L.L. 1996b. Einiges über die Handschrift Leiden 399,1 und die arabisch-lateinische Übersetzung von Gerhard von Cremona. In History of mathematics: States of the art, ed. J. Dauben, M. Folkerts, and H. Wussing, 173–205. San Diego: Academic Press.
Busard, Hubertus L.L. 2005. Campanus of Novara and Euclid’s Elements, 2 vols. Stuttgart: Franz Steiner Verlag.
Busard, Hubertus L.L., and Menso Folkerts. 1992. Robert of Chester’s (?) redaction of Euclid’s Elements, the so-called Adelard II Version, 2 vols. Basel-Boston-Berlin: Birkhäuser Verlag.
Clagett, Marshall. 1978. Archimedes in the Middle Ages. Volume iii: The fate of the medieval Archimedes, 1300–1565. Philadelphia: American Philosophical Society.
Corry, Leo. 2004. Modern algebra and the rise of mathematical structures, 2nd ed. Basel-Boston-Berlin: Birkhäuser.
Corry, Leo. forthcoming. The law of distributivity in the medieval traditions of Euclid’s Elements: Between geometry and arithmetic. (Cited throughout as [LC2]).
Corry, Leo, and Norbert Schappacher. 2010. Zionist internationalism through Number Theory: Edmund Landau at the opening of the Hebrew University in 1925. Science in Context 23(4): 427–471.
Curtze, Maximilian. 1899. Anaritii in decem libros primos elementorum Euclidis commentarii ex interpretatione Gherardi Cremonensis in códice Cracoviense 569 servata, Leipzig: Teubner (Euclidis Opera Omnia, I.L. Heiberg et H. Menge (eds.), supplementum).
Curtze, Maximilian. 1902. Der Liber Embadorum des Abraham bar Chijja Savasorda in der Übersetzung des Plato von Tivoli. Abhandlungen zur Geschichte der mathematischen Wissenschaften 12: 1–183.
Djebbar, Ahmed. 2005. L \(\text{' }\) algèbre arabe. Genèse d’un art. Paris: Vuibert.
Dold-Samplonius, Yvonne. 1987. Developments in the solution to the Equation \(cx^{2}+bx=a\) from al-Khwarizmi to Fibonacci. In From deferent to equant: A volume of studies in the history of science in the ancient and medieval Near East in Honor of E.S. Kennedy, vol. 500, ed. David A. King, and Georg Saliba, 71–87. New York: Annals of the New York Academy of Sciences.
Eastwood, Bruce S. 2007. Ordering the heavens: Roman astronomy and cosmology in the Carolingian renaissance. Brill: Leiden.
Folkerts, Menso. 1970. Boethius “Geometrie II”: ein mathematisches Lehrbuch des Mittelalters. Wiesbaden: Franz Steiner.
Folkerts, Menso. 1981. The importance of the Pseudo-Boethian Geometria during the Middle Ages. In Boethius and the Liberal Arts: A collection of essays, Berne, ed. M. Masi, 187–209, (Reprinted in Menso Folkerts 2003), Essays on early medieval mathematics: The Latin tradition. Aldershot: Ashgate).
Folkerts, Menso. 1989. Euclid in medieval Europe. Winnipeg: The Benjamin Catalogue.
Folkerts, Menso. 2004. Leonardo Fibonacci’s knowledge of Euclid’s Elements and of other mathematical texts. Bollettino di Storia della Scienze Matematiche 24: 93–114.
Folkerts, Menso. 2006. The development of mathematics in medieval Europe: The Arabs, Euclid, Regiomontanus. Aldershot: Ashgate Publishing Limited.
Freudenthal, Hans. 1977. What is Algebra and What has it been in History. Archive for History of Exact Sciences 16(3): 189–200.
Fried, Michael N., and Sabetai Unguru. 2001. Apollonius of Perga’s Conica: Text, Context, Subtext. Leiden: Brill.
Goldstein, Bernard. 1965. A treatise on Number Theory from a tenth century Arabic source. Centaurus 10: 124–160.
Goulding, Robert. 2010. Defending Hypatia: Ramus, Savile, and the renaissance rediscovery of mathematical history. Dordrecht, Heidelberg, London, New York: Springer.
Guillaumin, Jean-Yves. 2012. Boethius’ De institutione arithmetica and its influence on posterity. In A companion to Boethius in the Middle Ages, ed. Noel H. Kaylor, and Philip E. Phillips, 135–162. Leiden: Brill.
Guttmann, Yehiel Michael HaCohen. 1912–1913. Chibbur Ha-Meschicha WeHa-Tischboreth: Lehrbuch der geometrie des Abraham bar Chija, vol. 2. Berlin: Schriften des Vereins Mekize Nirdamim.
Heath, Thomas. 1956 [1908], The thirteen Books of Euclid’s Elements. New York: Dover.
Heath, Thomas. (1981) [1921]. History of Greek mathematics, vol. 2. New York: Dover.
Heiberg, Johan Ludvig, and Heinrich Menge. 1883–1893. Euclidis opera omnia. Ediderunt et latine interpretati sunt I. L. Heiberg et H. Menge, vol. 12. Lepzig: Teubner.
Hogendijk, Jan P. 2005. Al-Nayrīzī’s influence in the West. (Downloaded February 14, 2010, from http://www.jphogendijk.nl/publ/naywest.pdf).
Høyrup, Jens. 1986. Al-Khwârizmî, Ibn Turk, and the Liber Mensurationum: On the origins of Islamic Algebra. Erdem 2: 445–484.
Høyrup, Jens. 1988. Jordanus de Nemore, 13th century mathematical innovator. Archive for History of Exact Science 38: 307–363.
Høyrup, Jens. 1998. A new art in ancient clothes. Itineraries chosen between scholasticism and baroque in order to make Algebra appear legitimate, and their impact on the substance of the discipline. Physis, Nuova Serie 35: 11–50.
Høyrup, Jens. 2001. On a collection of geometrical riddles and their role in the shaping of four to six ‘Algebras’. Science in Context 14(1–2): 85–131.
Høyrup, Jens. 2010. Hesitating progress: the slow development toward algebraic symbolization in abbacus and related manuscripts, c. 1300 to c. 1550. In Philosophical aspects of symbolic reasoning in Early Modern Mathematics (Studies in Logic, 26), ed. Albrecht Heeffer, and Maarten Van Dyck, 3–56. London: College Publications.
Hughes, Barnabas. 1981. Jordanus de Nemore. De numeris datis. A Critical edition and translation. Berkeley–Los Angeles–London: University of California Press.
Hughes, Barnabas. 2008. Fibonacci’s De practica geometrie. New York: Springer (Sources and Studies in the History of Mathematics and Physical Sciences).
Kibre, Pearl. 1981. The Boethian De institutione arithmetica and the quadrivium in the thirteenth century University Milieu at Paris. In Boethius and the liberal arts: A collection of essays, ed. Michael Masi, 67–80. Bern/Frankfurt: Peter Lang.
Klein, Jacob. 1968. [1934–1936], Greek mathematical thought and the origin of Algebra (Translated by Eva Brann. With an appendix containing Vieta’s Introduction to the analytical art, translated by J. Winfree Smith). Cambridge, MA: MIT Press.
Lange, Gerson. 1909. Sefer Maassei Chosheb. Die Praxis des Rechners. Ein hebräisch-arithmetisches Werk des Levi ben Gerschom aus dem Jahre 1321. Frankfurt am Main: Louis Golde.
Lefèvre d’Étaples, Jacques. 1496. Arithmetica decem libris demonstrate. Paris: Johannes Higman and Wolfgang Hopyl.
Levey, Martin. 1966. The Algebra of Abū Kāmil. Kitāb fī al-jābr wa’l-muqābala, in a commentary by Mordecai Finzi (Hebrew Text, Translation and Commentary with Special Reference to the Arabic Text). Madison: University of Wisconsin Press.
Lévy, Tony. 1992. Gersonide, commentateur d’Euclide: Traduction annotée de ses gloses sur les Elements. In Studies on Gersonides: A Fourteenth-Century Jewish Philosopher-Scientist. Collection de Travaux de L \(\text{' }\) Académie Internationale d’Histoire des Sciences, vol. 36, ed. Gad Freudenthal, 83–148. Leiden: Brill.
Lévy, Tony. 1997a. Les ‘Eléments’ d’Euclide en hébreu (XIIIe–XVIe siècles). In Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque, ed. M. Aouad, A. Elamrani-Jamal, and A. Hasnaoui, 79–94. Leuven: Peeters.
Lévy, Tony. 1997b. Une version hébraïque inédite des ‘Eléments’ d’Euclide. In Les voies de la science grecque, ed. D. Jacquart, 181–239. Geneva: Droz.
Lévy, Tony. 1997c. The establishment of the mathematical bookshelf of the medieval Hebrew scholar: Translations and translators. Science in Context 10(03): 431–451.
Lévy, Tony. 2001. Les débuts de la littérature mathématique hébraïque: la géométrie d’Abraham bar Ḥiyya (XIe–XIIe s.). Micrologus 9: 35–64.
Lo Bello, Anthony. 2003a. Gerard of Cremona’s translation of the commentary of Al-Nayrīzī on Book I of Euclid’s Elements of geometry. With an introductory account of the twenty-two early extant Arabic manuscripts of the Elements. Leiden: Brill.
Lo Bello, Anthony. 2003b. The commentary of Albertus magnus on Book I of Euclid’s Elements of geometry. Leiden: Brill.
Lo Bello, Anthony. 2009. The commentary of al-Nayrīzī on Books II-IV of Euclid’s Elements of geometry. With a translation of that portion of Book I missing from MS Leiden Or. 399.1, but present in the newly discovered Qom manuscript ed. Rüdiger Arnzen. Leiden: Brill.
Luckey, Paul. 1941. Tābit b. Qurra über den geometrischen Richtigkeitsnachweis der Auflösung der quadratischen Gleichungen. Sächsischen Akademie der Wissenschaften zu Leipzig. Mathematisch-physische Klasse. Berichte 93: 93–114.
Millás-Vallicrosa, José María. 1931. Abraam bar Hiia, Llibre de geometría. Hibbur hameixihà uehatixboret. Barcelona: Editorial Alpha.
Moyon, Mark. 2007. La tradition algébrique arabe du traité d’Al-Khwârizmî au Moyen Âge latin et la place de la Géométrie. In Histoire et enseignement des mathèmatiques. Rigueurs, erreurs, raisonnements, ed. Evelyne Barbin, and Dominique Bénard, 289–318. Lyon: INRP.
Mueller, Ian. 1981. Philosophy of mathematics and deductive structure in Euclid’s Elements. Cambridge, MA: MIT Press.
Murdoch, John. 1966. Euclides Graeco-Latinus: A Hitherto unknown medieval Latin translation of the Elements made directly from the Greek. Harvard Studies in Classical Philology 71: 249–302.
Murdoch, John. 1968. The medieval Euclid: Salient aspects of the translations of the Elements by Adelard of Bath and Campanus of Novara. Revue de synthèse (ser.Il) l: 64–94.
Murdoch, John. 1971. Euclid: Transmission of the Elements. Dictionary of Scientific Biography 4: 437–459.
Murdoch, John. 2003. Transmission into use: The evidence of Marginalia in the medieval Euclides Latinus. Revue d’histoire des sciences 56(2): 369–382.
Neal, Katherine. 2002. From discrete to continuous: The broadening of the number concepts in Early Modern England. Dordrecht: Kluwer.
Netz, Reviel. 1999. The shaping of deduction in Greek mathematics: A study in cognitive history. Cambridge: Cambridge University Press.
Oaks, Jeffrey. 2001. Geometry and proof in Abū Kāmil’s Algebra. In Actes du 10ème Colloque Maghrébim sur l’Histoire des Mathématiques Arabes, 234–256. Tunis: L\(\text{' }\)Association Tunisienne des Sciences Mathématiques.
Oaks, Jeffrey. 2011. Al-Khayyām’s scientific revision of Algebra. Suhayl: Journal for the History of the Exact and Natural Sciences in Islamic Civilisation 10: 47–75.
Puig, Luis. 1994. El De Numeris Datis de Jordanus Nemorarius como sistema matemático de signos. Mathesis 10: 47–94.
Rabinovitch, Nahum L. 1970. Rabbi Levi ben Gershon and the origins of mathematical induction. Archive for History of Exact Sciences 6: 237–248.
Rommevaux, Sabine. 1999. La proportionnalité numérique dans le Livre VII des Éléments de Campanus. Revue d’histoire des mathématiques 5: 83–126.
Rommevaux, Sabine. 2008. The transmission of the Elements to the Latin West: three case studies. In The Oxford handbook of the history of mathematics, ed. Eleanor Robson and Jackie Stedall, 687–706. Oxford: Oxford University Press.
Rommevaux, Sabine, Ahmed Djebbar, and Bernard Vitrac. 2001. Remarques sur l’Histoire du Texte des Eléments d’Euclide. Archive for History of Exact Sciences 55: 221–295.
Rose, Paul Lawrence. 1975. The Italian Renaissance of mathematics: Studies on humanists and mathematicians from Petrarch to Galileo. Genève: Librairie Droz.
Rosen, Frederic 1831. The Algebra of Mohammed ben Musa. London: Murray.
Saito, Ken. (2004) [1985]. Book II of Euclid’s Elements in the light of the theory of conic sections. Historia Scientiarum 28: 31–60 (Reprinted in Jean Christianidis (ed.), Classics in the History of Greek Mathematics, Boston Studies in the Philosophy of Science, Vol. 240, Dordrecht-Boston: Kluwer, pp. 139–168).
Saito, Ken, and Nathan Sidoli. 2012. Diagrams and arguments in ancient Greek mathematics: Lessons drawn from comparisons of the manuscript diagrams with those of modern critical editions. In The history of mathematical proof in ancient traditions, ed. Karine Chemla, 135–162. Cambridge: Cambridge University Press.
Sarfatti, Gad B. 1968. Mathematical terminology in Hebrew Scientific Literature of the Middle Ages
 . Jerusalem: Magnes Press.
. Jerusalem: Magnes Press.Sesiano, Jacques. 1987. Survivance médiévale en Hispanie d’un problème né en Mésopotamie. Centaurus 30(1): 18–61.
Sesiano, Jacques. 1993. La version latine médiévale de l’Algèbre d’Abû Kâmil. In Vestigia Mathematica. Studies in Medieval and Early Modern Mathematics in Honour of H. L. L. Busard, ed. Menso Folkerts, and Jan P. Hogendijk, 315–452. Amsterdam et Atlanta: Rodopi.
Sigler, Laurence E. 2002. Fibonacci’s Liber Abaci. A translation into Modern English of Leonardo Pisano’s Book of Calculation. New York: Springer (Sources and Studies in the History of Mathematics and Physical Sciences).
Simi, Annalisa. 2004. L\(\text{' }\)eredità della Practica geometriae di Leonardo Pisano nella geometria del basso Medioevo e del primo Rinascimento. Bollettino di Storia della Scienze Matematiche 24: 9–43.
Simonson, Shai. 2000a. The missing problems of Gersonides—A critical edition. Historia Mathematica 27(3): 243–302.
Simonson, Shai. 2000b. The missing problems of Gersonides—A critical edition. Historia Mathematica 27(4): 384–431.
Tummers, Paul M.J.E. 1980. The commentary of Albert on Euclid’s Elements of Geometry. In Albertus Magnus and the Sciences: Commemorative Essays, ed. J.A. Weisheipl, 479–498. Toronto: Pontifical Institute of Mediaeval Studies.
Tummers, Paul M.J.E. 1994. Anaritius’ commentary on Euclid. The Latin translation I–IV (Artistarium Supplementa IX). Nijmegen: Ingenium Publishers.
Unguru, Sabetai. 1975. On the need to rewrite the history of Greek mathematics. Archive for History of Exact Sciences 15: 67–114.
Unguru, Sabetai and David Rowe. 1981–1982a. Does the Quadratic Equation have Greek Roots? Libertas Mathematica 1: 1–49.
Unguru, Sabetai, and David Rowe. 1981–1982b. Does the Quadratic Equation have Greek Roots? Libertas Mathematica 2: 1–62.
van der Waerden, Bartel L. 1976. Defense of a ‘Shocking’ point of view. Archive for History of Exact Sciences 15: 199–210.
Vitrac, Bernard. 2003. Les scholies grecques aux Éléments d’Euclide. Revue d’histoire des sciences 56: 275–292.
Vitrac, Bernard. 2004. A propos des démonstrations alternatives et autres substitutions de preuves dans les Éléments d’Euclide. Archive for History of Exact Sciences 59: 1–44.
Vitrac, Bernard. 2011. Faut-il réhabiliter Héron d’Alexandrie? Montpellier: France. (Downloaded May 02, 2012, from http://hal-paris1.archives-ouvertes.fr/hal-00454027).
Vitrac, Bernard, and Maurice Caveing. 1990. Euclide d’Alexandrie. Les Éléments. Traduit du texte de Heiberg (Vol. I. Introduction générale par Maurice Caveing. Livres I–IV: géométrie plane. Traduction et commentaires par Bernard Vitrac). Paris: Presses Universitaires de France.
Vlasschaert, Anne-Marie. 2012. Le Liber Mahameleth: Édition critique et commentaries. Stuttgart: Franz Steiner Verlag.
Weil, André. 1978. Who betrayed Euclid? Archive for History of Exact Sciences 19: 91–94.
Weinberg, Josef. 1935. Die Algebra des Abū Kāmil Šoǧā’ben Aslam. München: Druck der Salesianischen Offizin.
Acknowledgments
I want to pay my debt of gratitude to several friends and colleagues who read previous versions of this text, or parts of it, answered queries and sent me reading material, raised questions, and suggested ideas and advanced critical views: Fabio Acerbi, Sonja Brentjes, Karine Chemla, Menso Folkerts, Jan Hogendijk, Jens Høyrup, Tony Levi, Anthony Lo Bello, Mark Moyon, Jeffrey Oaks, Sabine Rommevaux, Ken Saito, Shai Simonson, and Roy Wagner. Special thanks I owe to my friends Michael Fried and Miki Elazar for help and patience with translations of difficult passages from Latin and Greek, and to Veit Probst in Heidelberg, without whose kind mediation I would have had a much harder time in gathering all the material needed to complete this work. Last, but not least, hearty thanks go to Len Berggren, to whom I submitted this article for publication. His very detailed reading and thoughtful editorial suggestions helped me significantly improve (and somehow shorten) the entire text.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: Len Berggren.
Dedicated to my dear friend Sabetai Unguru on his 82th birthday.
Rights and permissions
About this article
Cite this article
Corry, L. Geometry and arithmetic in the medieval traditions of Euclid’s Elements: a view from Book II. Arch. Hist. Exact Sci. 67, 637–705 (2013). https://doi.org/10.1007/s00407-013-0121-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-013-0121-5





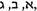
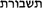
 . Jerusalem: Magnes Press.
. Jerusalem: Magnes Press.