Abstract
In Prawitz’s semantics, the validity of an argument may be defined, either relatively to an atomic base which determines the meaning of the non-logical terminology, or relatively to the whole class of atomic bases, namely as logical validity. In the first case, which may be qualified as local, one has to choose whether validity of arguments is or not monotonic over expansions of bases, while in the second case, which may be qualified as global, one has to choose whether the reduction functions which justify non-primitive inferences are or not base-depending. I claim that these oppositions enjoy some conceptual symmetries, and that these symmetries may be understood as putting restrictions on one’s choice both at the local and at the global level. This produces two different proof-theoretic semantics in line with Prawitz’s tenets. However, I also argue that the symmetries stem from a deeper interaction within Prawitz’s semantics, i.e. non-logical meanings vs interpretation of rules. This interaction is in turn based on some primitive ingredients which, when suitably combined, produce other two Prawitz-compatible readings. The four readings form a diagram where some order relations hold. I finally claim that this diagram is complete, namely that, if we combine the ingredients in ways other than those giving rise to the four readings above, we obtain nothing new, or nothing compatible with general semantic requirements. Thus, symmetries between the local and the global level, and interaction between non-logical meaning and interpretation of rules, produce a complete classification of potential Prawitzian semantics.
Similar content being viewed by others
Notes
In what follows, I will simply speak of inferences and justifications for them, but what I will be saying should be understood as applying also to inferences rules and justifications for these rules. As we said, although we will focus on argument structures, the arbitrary inferences occurring in these structures may be conceived of as instantiating certain rules. Of course, the distinction between (justifying) inferences and (justifying) rules becomes crucial when dealing with some issues in Prawitz’s semantics, but I will not go through these details here.
The point raised here is even more visible in Prawitz’s theory of grounds (Prawitz, 2015), where validity is not defined globally for structures where inferences occur but, locally, for inferences themselves. Each inference is associated to a function which is expected to transform evidence for the premises into evidence for the conclusion. The functions associated to introduction inferences are meaning-constitutive, and produce evidence by default. The functions associated to non-introductory inferences are instead non-primitive, and must be hence defined by suitable equations. This makes clear that inferences, when understood as simple pairs premises-conclusion, do nothing but indicate the domain and co-domain of a typed function. What the inferential transition is—what the inference “means”—is established by the equation. Still another way of looking at the issue is that of considering an inference act as a computation for transforming evidence for the premises into evidence for the conclusion. The premises-conclusion pair does not provide the computation instructions, but only indicates the input and output domains. The program is provided by the equation, and is executed by applying the inference. This is also why Prawitz’s semantics—more explicitly with the theory of grounds, but already with the valid arguments version, via the Curry-Howard isomorphism—can be understood as a semantics inspired by the formulas-as-types conception. A recent and thorough reconstruction and analysis of the wide historical roots and context of this approach can be found in Moriconi (Forthcoming). It should be mentioned, however, that Prawitz’s semantics has been also developed, e.g. in Piecha (2016); Piecha and Schroeder-Heister (2019), by following an alternative approach where, without speaking of justification functions, one defines a proof-based consequence-relation among formulas, and modulo abstract semantic principles. The “constructivist burden” is here put just on the deductive determination of the meaning of the non-logical constants. The overall picture is in a way broader and, in some respects, also more readily used for proving general results. In this paper, I preferred to stick to Prawitz (1971, 1973) original formulation, without implying with this, however, that such formulation should be considered as philosophically more satisfactory than the without-justification-functions approach.
Observe that this is equivalent to: for every \(\mathfrak {J}_i\), for every \(\langle \mathscr {D}_i, \mathfrak {J}_i \rangle\) for \(A_i\) valid over \(\mathfrak {B}\), the closure of \(\mathscr {D}\) obtained by replacing \(A_i\) with \(\mathscr {D}_i\), when paired with \(\mathfrak {J} \bigcup _{i \le n} \mathfrak {J}_i\), is valid over \(\mathfrak {B}\) (\(i \le n\)). Moreover, it is understood that closed atomic derivations over \(\mathfrak {B}\) are by default canonical and valid over \(\mathfrak {B}\)—precisely because \(\mathfrak {B}\) fixes the meaning of the non-logical terminology, and atomic derivations involve by definition no logical terminology. Similar observations hold for Definition 2.
Model-theoretically, this would amount to a consequence relation over a structure which fails, for the same \(\Gamma\) and A, on expansions of this structure. I shall come back to this. However, we can reduce to the case of non-monotonicity in the “traditional” sense, through what Piecha and Schroeder-Heister have called the export principle The idea is, roughly, that the rules of the atomic system of an atomic base \(\mathfrak {B}\) can be translated into a set of formulas \(\Delta _\mathfrak {B}\). An extension \(\mathfrak {B}^+\) of \(\mathfrak {B}\) will thus correspond to an extension \(\Delta ^+_\mathfrak {B}\) of \(\Delta _\mathfrak {B}\). So we have \(\Gamma \models ^\texttt {NE}_\mathfrak {B} A \Leftrightarrow \Gamma \cup \Delta _\mathfrak {B} \models ^\texttt {NE} A\). For more details see e.g. Piecha and Schroeder-Heister (2019).
I assumed that, when in each definition we have two focus elements, then they undergo the same range. Of course, we may allow for two focus elements to undergo different ranges, say
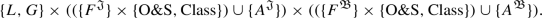
But the new combinations we obtain in this way turn out to be equivalent to some of those we have when focus elements undergo the same range. Observe that I am allowing for combinations where both elements are abstracted. Since the range concerns how the focus element(s) are to be dealt with in the definition, in the presence of combinations where both elements are abstracted, the range is, so to say, ineffective—in the cartesian product that I introduced in this footnote, this problem disappears. Observe also that, when both elements are either focused or abstracted at the global level, the quantification order does not really matter.
I am grateful to Cesare Cozzo, who raised the points on which this section is based. Of course, the empirical/non-empirical distinction is problematic in itself, as is problematic whether there actually is such a distinction. However, I shall not deal with these topics here.
Someone may claim that this is always the case, namely, that there are no analytical truths, since every rule-based definition is in principle revisable. I shall not try to establish whether this is the case or not. I just needed two examples, of which one “more analytical” than the other.
But observe also that \(\texttt {CanFly}(\texttt {Tweety})\) is derivable in the base, just as for \(\texttt {Gm}\) above. See footnote 7.
To this one may perhaps add a further element, call it \({\textbf {DF}}\), indicating some peculiar feature of the domain over which the argumentation step is meant to operate. As regards \(\texttt {Ind}\), for example, \({\textbf {DF}}\) may be some inductive characterisation of how the domain elements are built up, in which case \({\textbf {S}}\) is expected to be conclusive; when instead \({\textbf {DF}}\) is empty, \({\textbf {S}}\) is fallible, and it is null when \({\textbf {DF}}\) is meant to refer, e.g., to \(\mathbb {R}\). These are of course only very tentative suggestions, which may be developed in future works. It should be observed that the idea of “enriching” inference steps is also familiar from Prawitz’s theory of grounds (Prawitz, 2015), where as said an inference is not only given by premises and conclusion, but also by an operation for transforming grounds for the premises into grounds for the conclusion.
Let me additionally remark that Cozzo’s semantics might be useful for Prawitzian approaches also in the sense of providing a general theory of atomic bases This is because Cozzo’s theory of meaning is based on some notions of orders among words, given by inferential connections between rules involving, directly or indirectly, and implicitly or explicitly, those words. For more details, see Cozzo (1994).
Of course, when non-empirical domains are at issue, Gödel’s incompleteness theorems are in the background here—together with other limiting results. It may be interesting to remark that the idea according to which semantic content is not given once and for all, but needs to be each time refined through deeper and deeper—not necessarily formal—insights, is at the core of Gödel conceptual realism (Wang, 1997). However, it is not clear whether Prawitz’s constructivism is compatible with Gödel’s realism—but see (Crocco, 2016, 2019; Mertens, 2016).
References
Cozzo, C. (1994). Meaning and argument: A theory of meaning centred on immediate argumental role. Almqvist & Wiskell.
Crocco, G. (2016). Sinn/Bedeutung and Intension/Extension in Gödel’s Max Phil IX. In G. Crocco, & E.-M. Engelen (Eds.), Kurt Gödel philosopher-scientist (pp. 127–152).
Crocco, G. (2019). Informal and absolute provability: Some remarks from a gödelian perspective. Topoi, 38, 561–575. https://doi.org/10.1007/s11245-017-9515-3
Došen, K. (2015). Inferential semantics. In H. Wansing (Ed.), Dag Prawitz on proofs and meaning (pp. 147–162). https://doi.org/10.1007/978-3-319-11041-7_6.
Dummett, M. (1993). The logical basis of metaphysics. Harvard University Press.
Dummett, M. (1996a). What is a theory of meaning? (I) (pp. 1–33). Clarendon Press.
Dummett, M. (1996b). What is a theory of meaning? (II) (pp. 34–93). Clarendon Press.
Francez, N. (2015). Proof-theoretic semantics. College Publications.
Gentzen, G. (1935). Untersuchungen über das logische schließen i, ii. Mathematische Zeitschrift, 39(176–210), 405–431. https://doi.org/10.1007/BF01201353
Mertens, A. (2016). Gödel’s distinction between objective and subjective concepts, taken from the analysis of the remark on page 16 in the Max Phil XI. In G. Crocco, & E.-M. Engelen (Eds.), Kurt Gödel philosopher-scientist (pp. 189–201).
Moriconi, E. (Forthcoming). From proof-objects to grounds. In A. Piccolomini d’Aragona (Ed.), Perspectives on deduction.
Piccolomini d’Aragona, A. (2023). Prawitz’s epistemic grounding: An investigation into the power of deduction. Springer. https://doi.org/10.1007/978-3-031-20294-0
Piecha, T. (2016). Completeness in proof-theoretic semantics. In T. Piecha & P. Schroeder-Heister (Eds.), Advances in proof-theoretic semantics (pp. 231–251). https://doi.org/10.1007/978-3-319-22686-6_15.
Piecha, T., de Campos Sanz, W., & Schroder-Heister, P. (2015). Failure of completeness in proof-theoretic semantics. Journal of Philosophical Logic, 44, 321–335. https://doi.org/10.1007/s10992-014-9322-x
Piecha, T., & Schroeder-Heister, P. (2019). Incompleteness of intuitionistic propositional logic with respect to proof-theoretic semantics. Studia Logica, 107(1), 233–246. https://doi.org/10.1007/s11225-018-9823-7
Prawitz, D. (1965). Natural deduction: A proof-theoretical study. Almqvist & Wiskell.
Prawitz, D. (1971). Ideas and results in proof theory. In J. E. Fenstad (Ed.), Proceedings of the second Scandinavian logic symposium (pp. 235–307). Elsevier. https://doi.org/10.1016/S0049-237X(08)70849-8.
Prawitz, D. (1973). Towards a foundation of a general proof-theory. In P. Suppes, L. Henkin, A. Joja, & G. C. Moisil (Eds.), Proceedings of the fourth international congress for logic, methodology and philosophy of science, Bucharest, 1971, pp 225–250. Elsevier. https://doi.org/10.1016/S0049-237X(09)70361-1.
Prawitz, D. (2005). Logical consequence from a constructivist point of view (pp. 671–695). Oxford University Press.
Prawitz, D. (2015). Explaining deductive inference. In H. Wansing (Ed.), Dag Prawitz on proofs and meaning (pp. 65–100). Springer. https://doi.org/10.1007/978-3-319-11041-7_3.
Schroeder-Heister, P. (1984a). Generalized rules for quantifiers and the completeness of the intuitionistic operators \(\wedge\), \(\vee\), \(\rightarrow\), \(\forall\), \(\exists\). In E. Börger, W. Oberschelp, M. M. Richter, B. Schinzel, & W. Thomas (Eds.), Proceedings of the logic colloquium. Held in Aachen, July 18–23, 1983 (pp. 399-426). Springer. https://doi.org/10.1007/BFb0099494.
Schroeder-Heister, P. (1984b). A natural extension for natural deduction. Journal of Symbolic Logic, 49(4), 1284–1300. https://doi.org/10.2307/2274279
Schroder-Heister, P. (2006). Validity concepts in proof-theoretic semantics. Synthese, 148, 525–571. https://doi.org/10.1007/s11229-004-6296-1
Schroeder-Heister, P. (2008). Proof-theoretic versus model-theoretic consequence. In M. Peliš (Ed.), The logica yearbook 2007 (pp. 187–200).
Schroeder-Heister, P. (2012). The categorical and the hypothetical: A critique of some fundamental assumptions of standard semantics. Synthese, 187, 925–942. https://doi.org/10.1007/s11229-011-9910-z
Schroeder-Heister, P. (2018). Proof-theoretic semantics. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy.
Stafford, W. (2021). Proof-theoretic semantics and inquisitive logic. Journal of Philosophical Logic, 50, 1199–1229. https://doi.org/10.1007/s10992-021-09596-7
Tranchini, L. (2016). Proof-theoretic semantics, paradoxes and the distinction between sense and denotation. Journal of Logic and Computation, 26(2), 495–512. https://doi.org/10.1093/logcom/exu028
Tranchini, L. (2019). Proof, meaning and paradox: Some remarks. Topoi, 38, 591–603. https://doi.org/10.1007/s11245-018-9552-6
Troelstra, A. S., & van Dalen, D. (1988). Constructivism in mathematics (Vol. I): North-Holland.
Wang, H. (1997). A logical journey: From Gödel to philosophy. The MIT Press.
Wittgenstein, L. (1953). Philosophical investigations. Blackwell.
Acknowledgements
I am grateful to Bruno Bentzen, Cesare Cozzo, Ansten Klev, Thomas Piecha, Dag Prawitz, Peter Schroeder-Heister, Luca Tranchini, Will Stafford, Göran Sundholm, and the anonymous reviewers for most helpful comments and remarks on earlier drafts. Work on this article was supported by grant LQ300092101 from the Czech Academy of Sciences.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there is no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
d’Aragona, A.P. The proof-theoretic square. Synthese 201, 219 (2023). https://doi.org/10.1007/s11229-023-04203-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04203-5