Explicating ‘Explication’ via Conceptual Spaces

Abstract

Recent years have witnessed a revival of interest in the method of explication as a procedure for conceptual engineering in philosophy and in science. In the philosophical literature, there has been a lively debate about the different desiderata that a good explicatum has to satisfy. In comparison, the goal of explicating the concept of explication itself has not been central to the philosophical debate. The main aim of this work is to suggest a way of filling this gap by explicating ‘explication’ by means of conceptual spaces theory. Specifically, I show how different, strictly-conceptual readings of explication desiderata can be made precise as geometrical or topological constraints over the conceptual spaces related to the explicandum and the explicatum. Moreover, I show also how the richness of the geometrical representation of concepts in conceptual spaces theory allows us to achieve more fine-grained readings of explication desiderata, thereby overcoming some alleged limitations of explication as a procedure of conceptual engineering.

1 Introduction

In the last three decades, a renewal of interest in logical empiricism has led scholars to question the received view of Carnap’s philosophy (Stein 1992; Friedman 1999; Carsten and Awodey 2004; Friedman and Creath 2007). Thanks to this recent historical scholarship the concept of explication is now considered a pillar of Carnap’s mature thought (Carus 2007; Wagner 2012). Explication has also been at the center of a lot of methodological discussions, especially in connection with the metaphilosophical field of ‘conceptual engineering’, i.e. the “enterprise of assessing and improving our representational devices” (Cappelen 2018, p. 3). Can explication, understood as a general procedure for conceptual engineering, be useful for contemporary philosophy? If yes, how is this procedure exactly to be understood? What are the desiderata that a good explicatum has to satisfy?

In connection with these questions, a significant part of the philosophical debate over explication has focused on the desiderata that a good explicatum has to respect. However, it is still difficult to assess the usefulness of explication as a method of conceptual engineering. Many different criteria of adequacy have been proposed and discussed, but it is difficult to judge them due to the vagueness and ambiguity which sometimes characterize them. With the hope of improving this situation, in this paper I will propose a way of making precise the procedure of explication and its desiderata by means of the theory of conceptual spaces. Specifically, I will show how different readings of these desiderata can be made precise in terms of geometrical and topological constraints over the conceptual spaces of the explicandum and the explicatum.

My proposal relies on the theory of conceptual spaces (Gärdenfors 2000). Conceptual spaces have been successfully applied in different fields, proving themselves to be a powerful tool for representing different types of linguistic and conceptual phenomena, such as concept formation, metaphors, contextual effects, meanings (Gärdenfors 2000, 2014; Zenker and Gärdenfors 2015b). In philosophy, conceptual spaces have been used to account for vagueness-related phenomena for classificatory and comparative concepts and to model inductive inferences and other forms of conceptual manipulation (Douven et al. 2013; Decock et al. 2013; Decock and Douven 2014; Gärdenfors 2000; Sznajder 2016). In philosophy of science, conceptual spaces have been used to model various types of theory-change in physics as transformation of the related conceptual space(s) (Gärdenfors and Zenker 2011, 2013; Zenker and Gärdenfors 2015a; Masterton et al. 2017).

It is surprising, thus, that the theory of conceptual spaces has not played a more significant role in the philosophical debate over conceptual engineering. Since they have already been used to model vagueness and concept formation, conceptual spaces naturally present themselves as a useful tool for representing procedures of conceptual engineering that focus on the preservation of conceptual aspects, such as Carnapian explication. I will argue that the richness of the representation of concepts by means of conceptual spaces is indeed very useful for explication. I will show how this richness allows us to have more fine-grained readings of desiderata that overcome some alleged limitations of explication as a procedure of conceptual engineering.

The main goal of this work is, then, two-fold: to explicate the Carnapian procedure of explication by making precise various readings of its desiderata and to show the usefulness of conceptual spaces as a tool for modeling procedures of conceptual engineering. Of course, since this work constitutes only a first step towards the effort of explicating the concept of explication itself, one should not expect to find in what follows a full guide to explicate ‘explication’ in all its richness and complexity. Moreover, the applicability of my explication of ‘explication’ to a given case of explication rests on two assumptions:

Assumption 1

Both the explicandum and the explicatum are representable in conceptual spaces. Moreover, if the explicandum and the explicatum are represented in two different conceptual spaces, a suitable structure-preserving mapping from the conceptual space of the explicandum to the conceptual space of the explicatum is available.

Assumption 2

In assessing the adequacy of the given explication, all the desiderata are strictly-conceptual ones, i.e. they impose constraints only on the intrinsic relations between the explicandum and the explicatum.

The purpose of Assumption 1 is to ensure that all the concepts involved in a given explication can be adequately represented in conceptual spaces. The adequacy of conceptual spaces representation of concept formation and manipulation has been empirically tested for many types of concepts (Gärdenfors 2000; Zenker and Gärdenfors 2015b), but the exact scope of applicability of the theory is still unclear. It may be that very abstract concepts, such as Truth for instance, whose representational content is dubious, cannot be adequately modeled using conceptual spaces. That said, the many applications of conceptual spaces in different scientific fields arguably show that this assumption is not too restrictive. Furthermore, in Sect. 5 I will show how my explication of ‘explication’ by means of conceptual spaces theory is applicable to two paradigmatic cases of explication from the history of science, adding more support to this assumption.

As for Assumption 2, conceptual spaces are a tool for conceptual representation and as such they can represent just the intrinsic relations between concepts. Thus, as I will stress case by case in Sect. 4, it would be unclear at the very least how to represent in the context of conceptual spaces theory some desiderata that pose limitations on the target theory in which the explicatum is defined (such as being defined in a consistent theory, for instance) or other more pragmatical meta-theoretical virtues (such as predictive power) the scope of which is not restricted to the concepts involved in the explication. This assumption is required by the very nature of conceptual spaces theory. Nevertheless, I will support it in Sect. 4, showings how many different readings of explication desiderata proposed in the literature can be made precise by means of conceptual spaces theory.

In Sect. 2, I will present the concept of Carnapian explication, starting from Carnap’s remarks about it and surveying the related philosophical literature. I will focus on the desiderata that a good explicatum has to respect and on the different readings of them that have been proposed in the literature. I will also present some general critiques and alleged limitations of explication as a procedure of conceptual engineering and I will make methodologically more precise the goal of this paper, by distinguishing two senses of explicating ‘explication’. In Sect. 3, I will present the theory of conceptual spaces, both from a philosophical and a technical point of view. I will focus on some recent technical extensions of the theory, developed in order to treat vague and comparative concepts in the framework of conceptual spaces. In Sect. 4, I will show how the procedure of explication can be made precise inside the theory of conceptual spaces. Specifically, we will see how different readings of explication desiderata presented in the literature can be formalized as topological or geometrical constraints on the conceptual spaces related to the explicandum and the explicatum. I will also make evident how the representation of the explicandum and the explicatum in conceptual spaces allows us to state more fine-grained desiderata for the adequacy of an explication, which arguably show how explication can be successfully defended against some recent critiques. In Sect. 5, I will show how two paradigmatic cases of successful explications from the history of science can be represented and assessed in the context of my explication of ‘explication’: the scientific concept of temperature and the morphological concept of fish. Finally, I will draw some general conclusion about the significance of the results contained in this work for explication as a procedure of conceptual engineering and related debates in philosophy.

2 The Carnapian Concept of Explication

In Carnap’s own words:

“By the procedure of explication we mean the transformation of an inexact, prescientific concept, the explicandum, into a new exact concept, the explicatum. Although the explicandum cannot be given in exact terms, it should be made as clear as possible by informal explanations and examples.” (Carnap 1950, p. 3. Original emphases)

Explication is a procedure involving two concepts. On one side, we have the explicandum, belonging to natural language (or more generally an evolved language), the scope of which thus contains arguably an amount of vagueness and/or ambiguity. On the other side, we find the explicatum, belonging to a (more) precise language, the scope of which is characterized by explicit rules of use.

Explication is a two-step procedure. First, one has to clarify the explicandum, trying to explicitly state the intended meaning of the concept that one wants to explicate. Since the concept is still expressed in a natural language, an exact definition is not required. What Carnap requires from the explicator, instead, is to state some positive and negative instances of the explicandum, together with some description or (partial) rules of use (Carnap 1950, pp. 3–5). The goal of this first step, called by Carnap the ‘clarification of the explicandum’, is to clarify and (if necessary) to disambiguate the concept that one seeks to explicate. Then, we have the second step of the explication, which is the formulation of the explicatum in a certain target theory via an explicit definition or by stating its rules of use.

The purpose of explication is the substitution, relative to a specific function-context, of an inexact concept with a (more) precise one. In contemporary terms, explication is, then, a method of conceptual engineering.

A distinctive peculiarity of explication is that it is an inherently pragmatical procedure, i.e. its adequacy is not a matter of right or wrong, but of what is more or less satisfactory for the task that the explicator has in mind. Judging this adequacy is never an all or nothing matter; the explicator has always a certain degree of freedom in choosing the explicatum for substituting a given concept. In Carnap’s late terminology, as Stein stressed, questions about explication adequacy are thus external questions:

“The explicatum, as an exactly characterized concept, belongs to some formalized discourse – some ‘framework’. The explicandum (...) belongs ipso facto to a mode of discourse outside that framework. Therefore any question about the relation of the explicatum to the explicandum is an ‘external’ question; this holds, in particular, of the question whether an explication is adequate – that is, whether the explicatum does in some appropriate sense fully represent, within the framework, the function performed (let us say) ‘presystematically’ by the explicandum.” (Stein 1992, p. 280)

Even though explication is not a matter of right or wrong, one can still judge whether an explication is good or bad. In fact, external questions for Carnap can still be objects of rational discourse, although of the pragmatic kind of rationality that is often called instrumental. Relative to a specific purpose or function, one can still state various pragmatic meta-principles that a good explicatum has to respect. Carnap stated four desiderata that a good explicatum has to satisfy (Carnap 1950, pp. 5–8):

• Similarity: to the extent to which the other desiderata allow it, the explicatum ought to be as similar to the explicandum as possible (exact similarity, i.e. identity, is explicitly not required).

• Fruitfulness: the explicatum ought to be connected with other scientific concepts, in order to make as many generalizations as possible expressible within the theory in which it is defined.

• Exactness: rules of use of the explicatum ought to be stated in an exact form (e.g. definitions, axioms).

• Simplicity: the explicatum ought to be as simple as the other desiderata allow it to be.

These four desiderata hint at the theoretical virtues that a good explicatum must have, but they are too vague and ambiguous to constitute a practical guide for explicating a certain concept. Carnap never attempted to further develop these criteria. He instead developed various practical examples of what he considered good explicata for fundamental philosophical concepts, e.g. his works on logical probability as an explication of confirmation (Carnap 1950) or his efforts towards explicating our concepts of modality and analyticity (Carnap 1947). Using these and other examples, in science and philosophy, of formal notions that have replaced informal ones, various scholars have proposed refined and more precise versions of these. Indeed, explication has recently been proposed as one of the prominent methods of conceptual engineering. Let us survey this debate, then.

2.1 Discussing Explication Desiderata

To better structure the discussion, let us treat Carnap’s four desiderata, one by one.

Similarity. This is perhaps the desideratum that has most attracted the attention of scholars, due to its pivotal role in distinguishing explication from other forms of conceptual engineering. Since, as we have seen, the explicandum is normally a vague, informal concept and the explicatum is instead a (more) precise, formal notion, exact similarity is not required.¹ If, then, an explicatum is allowed to have a different extension than the explicandum, the question at issue is to which degree an explicatum has to be similar to the related explicandum.

Hanna argued that the explicatum has to agree with the explicandum in all clear-cut cases where the latter can be applied (Hanna 1967, pp. 34–36). This strict reading of the similarity requirement makes explication, as Hanna himself acknowledges, just a procedure for eliminating any vagueness from our informal concepts and it thus makes the explicatum a precisification of the explicandum. This can be clearly seen in Hanna’s formal explication of ‘explication’ where the (formal notion that seeks to explicate the) explicatum is technically a precisification of the (formal notion that seeks to explicate the) explicandum (Hanna 1967, pp. 37–38).

Another strict reading of the similarity requirement is Quine’s “synonymy in favored contexts”, i.e. synonymy with respect to all the contexts where the use of the explicandum is clear and precise (Quine 1961, p. 25). Both these readings seem in direct contrast with Carnap’s own examples, e.g. the explication of the concept fish in (Carnap 1950, p. 6), where he allows explicata to be concepts that explicitly reject clear, non-defective, positive instances of the explicandum. They also appear too narrow for any general procedure of conceptual engineering for science and philosophy. Often, in fact, as even Quine himself acknowledged later (Quine 1960, pp. 258–260), scientists change meanings and uses of pre-theoretical concepts for purely theoretical reasons, despite how clear a certain use of an explicandum originally is.

Brun has recently argued for a more liberal reading of the similarity requirement, which he understands as requiring the explicatum to preserve all the context-dependent instances of the explicandum (Brun 2016, pp. 1218–1219). The context is freely decided by the explicator in relation to the purpose for which the explicatum is expected to substitute the explicandum. Carnap also stressed the significance of the ‘clarification of the explicandum’, i.e. an informal explanation and list of examples (both positive and negative) that helps one to grasp the intended meaning-context for the explication. A well-known example of this decision of context are Tarski’s opening remarks before his explication of the concept of truth, where he stated that he is interested in explicating the context of truth-assertions like “‘snow is white’ is true” and not in explicating uses such as “you are a true friend” (Tarski 1956). Thus, according to this interpretation, an explicatum is allowed to diverge from the scope of the explicandum even in clear-cut cases of application of the latter if they are not within the specific context freely chosen by the explicator.

Brun also proposed, in a more recent work, to split the similarity requirement into two steps. The first step consists in adjusting the extension of the explicandum (implicitly fixing the context), thereby obtaining a sharpened ‘$explicandum_{2}$. The second step requires what Goodman calls ‘extensional isomorphism’, i.e. an injection from the extension of $explicandum_{2}$ to the extension of the explicatum (Brun 2017, pp. 11–13). This two-step reading is connected with Brun’s more general proposal of merging explication with (a particular interpretation of) Goodman’s method of reflective equilibrium. Brun acknowledges that the injection-requirement seem trivial for a single concept, but stresses its significance for explicating a system of concepts and overcoming some limitations of (what he takes to be) the linear-monoconceptual Carnapian picture of explication (Brun 2017).

Fruitfulness. Carnap vaguely described this desideratum in terms of relations to other concepts and generalization-power. He distinguished this generalization-power between two cases, i.e. “empirical laws in the case of a nonlogical concept, logical theorems in the case of a logical concept” (Carnap 1950, p. 7). This seems indeed a necessary condition for a good explication of certain kinds of concepts, but as a general rule, it seems not really useful (by itself). After all, every formal concept whatsoever can produce an infinity of generalizations and truths.²

Dutilh Novaes and Reck proposed to read fruitfulness, in a general Enlightenment liberation spirit à la Carus, as the improvement of the pragmatic and epistemic situation of an agent. They claimed that a fruitful explicatum has to make our reasoning more effective and more reliable, thereby proving itself to be a better cognitive tool (for a certain purpose) than the explicandum (Dutilh Novaes and Reck 2017, pp. 205–211).

Shepherd and Justus took fruitfulness to be, like similarity, a context-dependent desideratum, relative to the type of concept the explicandum is and the purpose that the explicatum has to perform (Shepherd and Justus 2015, pp. 395–400).

Exactness. Here the main question is whether exactness means (a certain level of) formal rigor. Formal frameworks were considered by Carnap, even after his tolerance turn, the benchmark of exactness and rigor. If one looks at his own efforts in explicating concepts like analyticity or confirmation, one finds always the explicatum defined in a formal framework. Should we therefore understand the exactness requirement simply as the request of formulating the explicatum within a formal framework? Hanna believes that this is not enough. He, in fact, claimed that a certain explicatum has always to have a perfectly clear extension, thereby (together with his aforementioned extensional reading of similarity) making the explicatum a complete precisification of the explicandum (Hanna 1967, p. 36).

These strictly-formal readings of the exactness requirement seem too narrow for a general procedure of conceptual engineering, especially considering the fact that Carnap (who was not exactly a sworn enemy of the use of formal methods in philosophy) warned against a strictly formal reading of the exactness requirement.³ Therefore, the exactness requirement has been understood in a comparative way, relative to the explicandum (Dutilh Novaes and Reck 2017, p. 201), allowing a certain open-endedness in the offspring of the procedure of explicating a certain concept. This comparative reading of exactness can be easily cashed-out in terms of vagueness, by requiring the explicatum to be less vague than the explicandum. Brun favored a weaker reading of comparative exactness, i.e. the explicatum should not be vaguer than the explicandum. Using as evidence Carnap’s aforementioned fish example, he argued that in some cases the explicatum is as vague as the explicandum (Brun 2016, pp. 1220–1221). He also stresses that Carnap hinted at an additional aspect of the exactness requirement in discussing the temperature example, namely, that usually quantitative concepts are preferable over qualitative and comparative ones because they allow us to make more fine-grained distinctions (Brun 2017, p. 1220).

Simplicity. Last and explicitly least, this desideratum is often left aside in the discussion about explication. Carnap stresses that simplicity is only a last resort when the explicator has to choose between different explicata that fulfill to the same degree the other, more important, desiderata (Carnap 1950, p. 7). Therefore, there is not much debate over what the simplicity requirement means. To my knowledge, only Brun’s treatment of explication includes a discussion of simplicity. He stresses that simplicity has to be understood not in the ontological Occamian sense (i.e. ontological parsimony) but as a syntactical-logical requirement on the definition of the explicatum and perhaps also on the overall structure of the target theory in which the explicatum is defined (Brun 2016, p. 1221).

Of course, one may add to these four desiderata other theoretical virtues that a good explicatum should possess. Perhaps, other possible desiderata could be general pragmatic and theoretic virtues that good scientific theories embody, such as explanatory power, predictive power, novelty, unification power, trans-theoretic coherence, and so on. Another, interesting, possible desideratum is due to Karl Menger, to whom Carnap (Carnap 1950, p. 7) acknowledged a certain debt in developing the idea of explication, who in discussing geometrical definitions stresses that a good explicatum “should extend the use of the word by dealing with objects not known or not dealt with in ordinary language” (Menger 1943, p. 5).

2.2 Recent Critiques of Explication

The discussion about the desiderata that a good explicatum has to respect has also sparked a more general methodological discussion about the dignity of explication as a procedure of conceptual engineering. Apart from the aforementioned well-known critique of Strawson, new critiques have emerged.⁴

For instance, Dutilh Novaes and Reck have recently argued that explication (and, more generally formalization) is an inherently paradoxical enterprise. Explication is paradoxical, according to them, because there is a tension between two of its most important desiderata, namely fruitfulness and similarity: similarity allegedly calls for a close relationship with the explicandum, while fruitfulness pushes the explicatum towards a more radical departure from the explicandum. They named this phenomenon “the paradox of adequate formalization” (Dutilh Novaes and Reck 2017, p. 211), claiming that it is nothing but another form of the well-known “paradox of analysis” (Beaney 2018).

Reck in another work stresses, in a Strawsonian fashion, that Carnapian explication has some blind spots, such as its strong focus on formal aspects, its strive for exactness, its unwillingness to take into account methodologically different alternatives (Reck 2012, pp. 106–114). Reck acknowledges that these blind-spots are far from being impossible to be mitigated by a more pragmatic and liberal theory of explication, but he argues that such a theory would lead us back to philosophical disputes of the very kind that explication was meant to overcome.

Other two limitations of explication as a general procedure for conceptual engineering are stressed, instead, by Brun, who argues that Carnapian explication is heavily limited by its focus on individual concepts (i.e. it does not take into account more complex entities such as systems of concepts) and by its linear structure that seems to describe a no-turning-back triumphant engineering from the explicandum to the explicatum, hiding thus the complexity of the dialectics between the two parts of explication.⁵ Brun argues that these two points can be mitigated via a more liberal recipe-approach to conceptual engineering, merging explication with Goodman’s reflective equilibrium.

2.3 Explicating ‘Explication’

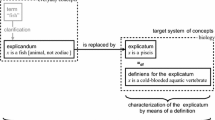
I already stated that the main goal of this work is to give an explication of ‘explication’. What does it mean, then, to explicate the concept of explication itself? It seems to me that this phrase can be understood (at least) in two different ways.

First, explicating ‘explication’ could consist in formally or informally giving a specific method for substituting a certain explicandum with a certain explicatum. This is the sense in which Hanna proposed his explication of ‘explication’ (Hanna 1967) and Brun recently gave us a recipe for explication (Brun 2016, 2017). Hanna’s explication is a formal procedure, Brun’s is stated as an informal method but both try to explicate ‘explication’ as a specific (formal/informal) procedure for replacing a particular reading of explication and its desiderata. There are of course further differences between the two proposals. As I said, Hanna is clearly explicating a very narrow, and very not Carnapian, sense of explication, while Brun gives a recipe for a very liberal clarification of what explication is. Nevertheless, for our current methodological discussion, they both instantiate the same sense of explicating ‘explication’. Let me refer to this sense of explicating ‘explication’ as the single-explicatum sense.

Secondly, a more general sense in which the task of explicating ‘explication’ could be understood is as the task of providing a precise bridge-theory in which the explicandum and the explicatum could be represented, thereby allowing a (more) precise judgment of the adequacy of explication efforts and a (more) exact representation of the (different readings of the) desiderata. This is what I will try to do using the theory of conceptual spaces in this work and, to my knowledge, is the first attempt of explicating ‘explication’ in this specific sense.⁶ This sense is more general because it does not only explicate a given clarification of a subset of explication desiderata, but it proposes instead some kind of meta-theory in which different readings of various desiderata of explication can be made precise. If the single-explicatum sense amounts to give a practical equivalent of a specific reading of explication, this more general sense of explicating ‘explication’ amounts to give a theory of explication. With the help of such a general explication of ‘explication’, external questions about explication adequacy can then be represented in a more precise manner while still remaining subject to instrumental rationality and pragmatical factors. The outcome of this sense of explicating ‘explication’ is a bridge theory within which (certain kinds of) different readings of explication and its desiderata can be precisely compared and applied to specific cases of conceptual engineering. Let me call this sense the meta-theoretical sense of explicating ‘explication’.

In this work, I propose an explication of ‘explication’ in the meta-theoretical sense. I will also show some examples of possible explications in the single-explicatum sense that can be proposed within my framework, but I will not endorse anyone of them as the favored reading of explication and its desiderata.

3 Conceptual Spaces

The theory of conceptual spaces (Gärdenfors 2000, 2014) has to be understood as a theory of mental representation. According to it, we represent information at three different levels (in order of ascending complexity): subconceptual (e.g. neural networks), conceptual, and symbolic (e.g. Fodor’s language of thought). The conceptual level is where the categorization process takes place and where we construct properties, concepts, meanings, and categories. The main tenet of conceptual spaces theory is that we can model what happens at this level geometrically.

Pivotal in the theory of conceptual spaces is the notion of quality dimension. The idea is that a quality dimension represents a particular (aspect of a) quality with respect to which objects can be judged as more or less similar. The more similar two objects are with respect to that quality, the closer their related points in that quality dimension. Examples of familiar concepts that can be modeled as quality dimensions include time, weight, size, and brightness. A quality dimension is a dimension in a strict geometrical sense, i.e. every quality dimension is equipped with a specific geometrical or topological structure. Quality dimension often come with a metric, i.e. with a distance function, but also qualitative measures of distances are allowed. Neither dimensions or the metrics are arbitrary, but are usually determined on the basis of a large set of similarity judgments via suitable techniques such as multidimensional scaling or principal component analysis (Douven and Gärdenfors 2019, p. 5).

Quality dimensions can be integral or separable. Two dimensions are integral iff to assign a value to an object in one of them implies simultaneously assigning a value in the other one. Dimensions that are not integral are called separable. Color perception dimensions, such as saturation and hue, are a familiar example of integral dimensions. Dimensions of shape and weight are instead examples of separable dimensions. Quality dimensions appear often related together in stable groups. A set of integral dimensions that are separable from all the other ones is called a domain. Examples of domains are the color domain (constituted by the dimensions of hue, saturation, and brightness) and the space domain (height,width, and depth). A conceptual space is, then, a collection of one or more domains.

A conceptual space is able to represent objects, properties, and concepts. Objects are represented as vectors. Properties are represented as certain kinds of regions in a domain. Natural properties are hypothesized to be (representable as) convex regions of a domain (Gärdenfors 2000, p. 71). Concepts, then, are certain kinds of sets of regions in a (possibly open-ended) number of domains. Natural concepts are sets of regions in a number of weighted domains equipped with information about how regions in different domains are correlated (Gärdenfors 2000, p. 105). It is then possible to distinguish between core and peripheral properties of concepts, by assigning different salience weights to different domains. In a similar fashion, singular dimensions can be weighted in order to account for contextual effects of various kind.

Gärdenfors then takes convexity to be the pivotal feature of regions representing natural properties and concepts. The necessity of convexity as a criterion of naturalness in conceptual spaces has been criticized by various scholars. Mormann highlighted that convexity requires the underlining conceptual space to be metrical or linear and it therefore strongly restricts the possible structure of the conceptual space (Mormann 1993, p. 220). He instead favored a pluralist approach to naturalness criteria, arguing that in many cases weaker topological notions such as connectedness or closedness are as good as convexity and they do not impose strong restrictions on the underlining structure of the space (Mormann 1993, pp. 226–239).

Recently, Hernández-Conde has strengthen the case against convexity as a naturalness criterion, arguing that this constraint is problematic both from a theoretical and a practical perspective. He claimed that the main arguments that Gärdenfors gave for convexity either require very strong assumptions on the underlining structure of the space or they work also for weaker requirements such as star-shapedness (Hernández-Conde 2017). Moreover, he showed how convexity appears to be problematic also from the inner perspective of conceptual spaces theory (Hernández-Conde 2017, pp. 4027–4034). I remain neutral on whether convexity is the right criterion of naturalness in conceptual spaces. In Sect. 4, I will show how a plurality of geometrical constraints can be used to make precise in conceptual spaces the fruitfulness of an explication, but as I stated in Sect. 2 I will not endorse any reading of explication desiderata as the correct one.

3.1 Technicalities

In the theory of conceptual spaces the fundamental notion of a quality dimension has to be understood as a proper geometrical dimension. Axioms and primitive relations of any dimension can be of any kind. Minimal requirements can be defined in terms of the relations of betweenness (B(a, b, c) ) and equidistance (E(a, b, c, d) ). Since the most fundamental task of a quality dimension is the assessment of similarities, what specifically characterizes a certain dimension is the notion of distance with which it is equipped. Dimensions can have either a qualitative (e.g. a notion of equidistance) or a quantitative (e.g. a certain metric) notion of distance. If a certain dimension is equipped with a quantitative distance function, it is then called a metric space. A function $d: S \times S \Rightarrow {\mathbb {R}}_{0}^{+}$ is called a distance function iff $\forall x,y,z \in S$: $d(x,y)\geqslant 0$, $d(x,y)= 0 \leftrightarrow x=y$, $d(x,y) = d(y,x)$, and $d(x,y) + d(y,z) \geqslant d (x,z)$. Examples of metrics, for a n-dimensional space, are the Euclidean metrics ($d_{E} (x,y)= \sqrt{\varSigma _{i} (x_{i}-y_{i})^{2}}$) and the city-block metrics ($d_{C} (x,y)= \varSigma _{i} | x_{i}-y_{i} |$).⁷ We can easily vary the scales of the different dimensions of a certain conceptual space by putting a weight $w_{i}$ on the distance function of the dimension i. Similarity is, then, an exponentially decaying function of distance (e.g. Shepard’s universal law of generalization $s_{ij}= e^{-c\cdot d_{ij}}$).

In a certain conceptual space S, consisting of a set of domains $\{ D_{1}, \ldots , D_{n}\}$, each made up of a set of integral dimensions $\{ d_{1}, \ldots , d_{m}\}$, we can represent objects as vectors $\langle v_{1}, \ldots , v_{j} \rangle$. Properties, then, are represented by regions S of a domain. We can define a region of a space as a set of points that respect certain criteria that we impose on the primitive relation: C(X, Y) , X connects with Y is minimally constrained by symmetry and reflexivity. A possible criterion for defining a region is connectedness, i.e. X is connected iff $\forall Y, Z (Y\cup Z = X \rightarrow C(Y,Z))$. A stronger criterion that can be imposed as a definition of region is star-shapedness relative to a point, i.e. X is star-shaped relative to a point $x_{0}$ iff $\forall z, \forall x\in X (B(x,z,x_{0}) \rightarrow z\in X)$. An even stronger criterion is convexity, i.e. X is convex iff $\forall z, \forall x,y \in C (B(x,z,y) \rightarrow z\in C)$ (Fig. 1). Concepts are represented, then, as multi-domain bundles of properties $X_{1}, \ldots , X_{n}$, together with salience weights $w_{i}$ on the domains and cross-domain correlations.

Fig. 1

A convex (a) and a star-shaped (b) region

One of the most promising applications of conceptual space is concept formation and categorization. Gärdenfors proposes a very smooth combination of prototype theory (Rosch 1975) together with the spatial tessellation technique called Voronoi diagrams (Okabe et al. 2000). The basic tenet of prototype theory is that not every instance of a concept is equally representative, i.e. there is a (partial or total) order of representativeness amongst instances of the concept. The most representative instance of the concept is called a prototype. A Voronoi diagram, instead, is a tessellation of a space that, provided with a set of points, divides the space in cells, each cell having as a center one of the points in the original set and containing all the points that lie closer to its center than to the centers of the other cells. More accurately, for any n-dimensional space and any set of pairwise distinct points of S $P= \{ p_{1}, \ldots , p_{k} \}$, the Voronoi diagram generated by P is the set $V(P) = \{ v(p_{i}) | p_{i}\in P \}$, where $v(p_{i})$ is the region $v(p_{i}) = \{ p | d(p,p_{i}) \leqslant d(p, p_{j}) \forall j \in \{ 1, \ldots , k \} \}$ and it is called the Voronoi polygon/polyhedron associated with $p_{i}$.

The theory of conceptual spaces has been recently extended in order to treat vague (Douven et al. 2013) and comparative concepts (Decock and Douven 2014; Dietz 2013; Decock et al. 2013).

The first step for dealing with vagueness in conceptual spaces is to substitute unique prototypes with prototypical areas, thereby making the generator set P become a set of regions. Then, the basic idea is to consider all the possible Voronoi diagrams that can be built from choosing a single point in each generator region. Intuitively, we treat vagueness in a way similar to the supervaluationist account, because every possible Voronoi diagram represents a possible completion of the tessellation of the space and thus a possible way of deciding the borderline cases of the concept involved. Then, we project all these possible Voronoi diagrams onto each other. From the result of this projection, called a collated Voronoi diagram, we can define boundary regions of categorization in order to accurately represent borderline cases of concepts (Fig. 2).

Fig. 2

A normal (a) and a collated (b) Voronoi Diagram

More formally, consider the restricted Voronoi polygon associated with $p_{i}$, i.e. the region made of all points that lie strictly closer to $p_{i}$ than to the other central points: ${\underline{v}} (p_{i}) = \{ p | d (p, p_{i}) < d (p,p_{j}) \forall j \in \{ 1, \ldots , k \} \}$. Then, let $R = \{ r_{1}, \ldots , r_{k} \}$ be a set of pairwise distinct regions and consider the set $\varPi (R) = \prod _{i=1}^{k} r_{i} = \{ \langle p_{1} , \ldots , p_{k} \rangle | p_{i} \in r_{i} \}$, i.e. the set of all sequences containing exactly one point out of each region of R. Consider, then, the set of all Voronoi diagrams generated by elements of $\varPi (R)$, i.e. ${\mathcal {V}}(R) = \{ V(P) | P \in \varPi (R) \}$; the set of all Voronoi polygons associated with the various points in a region $r_{i}\in R$, i.e. $\{ v(p) \}_{r_{i}\in R} := \{ v(p) | p \in r_{i} \wedge v(p) \in V(P) \in {\mathcal {V}}(R) \}$; and the set of all restricted Voronoi polygons associated with the various points in a region $r_{i}\in R$, i.e. $\{ {\underline{v}}(p) \}_{r_{i}\in R} := \{ {\underline{v}}(p) | p \in r_{i} \wedge v(p) \in V(P) \in {\mathcal {V}}(R) \}$. We can then construct the collated Voronoi diagram generated by R, ${\underline{U}} (R) = \{ {\underline{u}} (r_{i}) | 1 \leqslant i \leqslant k \}$, where each ${\underline{u}} (r_{i}) = \bigcap \{ {\underline{v}} (p) \}_{r_{i}\in R}$ is the collated polygon associated with $r_{i}$, i.e. the set of all points that lie in the restricted polygon of $r_{i}$ in all the possible Voronoi diagrams $V(P) \in {\mathcal {V}}(R)$. Recovering our analogy with the supervaluationist treatment of vagueness, the notion of the collated polygon associated with a region corresponds to the notion of super-truth in supervaluationism. We also have the expanded polygon associated with a region ${\overline{u}} (r_{i}) = \bigcup \{ v(p) \}_{r_{i}\in R}$, which is the dual notion of the restricted one and thus it is analogous to the supervaluationist notion of sub-truth. Then, we can define the boundary region associated with a collated polygon ${\underline{u}} (r_{i}) \in {\underline{U}} (R)$ as the set ${\overline{u}} (r_{i}) {\setminus } {\underline{u}} (r_{i})$, which is the set of all points that lie in the expanded polygon but not in the collated polygon associated with a given region.

The account of comparative concepts builds upon the vagueness framework, by adding to it an account of graded-membership in conceptual spaces. The informal idea for graded-membership in this account, which traces back to a proposal by Kamp and Partee, is that the degree to which an object falls under a concept is given by the amount of possible completions that group the object with the clear-cut instances of the concept (Kamp and Partee 1995). Extreme cases of graded membership are, then, objects that always fall under the concept, which receive a degree of membership of 1, and objects that never fall under that concept, which get a degree of membership of 0.

In the conceptual spaces framework, elements of the set $\varPi (R)$ play the role of completions. The simplified idea (for concepts with a finite amount of prototypes) behind the membership function for a given object is to calculate the ratio between the k-tuples of $\varPi (R)$ that generates Voronoi diagrams including the object into the scope of the concept and the number of elements in $\varPi (R)$. The general idea for constructing a membership function for prototypical areas containing an infinite number of prototypical instances is to measure the set of positive completions for a given object in terms of the volume occupied by the related coordinates in the related product space. More formally, we represent each completion by means of a $m \times k$-tuple $\langle x_{1_{1}}, \ldots , x_{1_{m}}, \ldots , x_{k_{1}}, \ldots , x_{k_{m}} \rangle$ of real numbers, where $\langle x_{1}, \ldots , x_{k} \rangle \in \varPi (R)$ and $x_{i_{1}}, \ldots , x_{i_{m}}$ are the spatial coordinates of a prototypical instance $p_{i}$. Then we can build for any point a, any concept $C_{i}$ with prototypical area $r_{i}$, and any distance function d the proportions of completions $S_{a,i}$ (volume of positive completions), relative to the set $\varPi (R)$:

$$\begin{aligned} \mu ^{*} (S_{a,i}) = \frac{\mu (S_{a,i})}{\mu (\varPi (R))} \end{aligned}$$

Where $\mu (S_{a,i})$ measures the set of positive completions, i.e. :

$$\begin{aligned}&\{ \langle x_{1_{1}}, \ldots , x_{1_{m}}, \ldots , x_{k_{1}}, \ldots , x_{k_{m}} \rangle | d (a, \langle x_{i_{1}}, \ldots , x_{i_{m}}\rangle ) \\&\quad <d (a, \langle x_{j_{1}}, \ldots , x_{j_{m}}\rangle ) \forall \langle x_{j_{1}}, \ldots , x_{j_{m}}\rangle \in r_{j} \, s.t. \, i \ne j \} \end{aligned}$$

and $\mu (\varPi (R))$ measures the set of all possible completions, i.e.

$$\begin{aligned} \int {\mathcal {I}}_{\varPi (R)} (\langle x_{1_{1}}, \ldots , x_{1_{m}}, \ldots , x_{k_{1}}, \ldots , x_{k_{m}} \rangle ) dx_{1_{1}} \ldots dx_{k_{m}}. \end{aligned}$$

We can then define the membership function of an object a relative to a concept $C_{i}$ as $M_{C_{I}} (a) = \mu ^{*} (S_{a,i})$. Thanks to this function we obtain a very smooth treatment of comparative concepts defining, for two individuals $i, i'$, i is C-er than $i'$ iff $M_{C} (i) > M_{C} (i')$. Comparative concepts of different types, such as ‘a is more typically C then b’ or ‘a is more C-ish then b’, can be defined more easily in terms of the Hausdorff distance (a general way of calculating the distance between sets of points) (Decock et al. 2013, pp. 76–77).

4 Explication in Conceptual Spaces

The general idea behind my proposal is the following, namely, to explicate ‘explication’ in the meta-theoretical sense (see Sect. 2) by means of conceptual spaces theory. Thus, I have to show how representing the explicandum and the explicatum in conceptual spaces allows a more precise judgment of the adequacy of a given explication. As presented in Sect. 2, the adequacy of an explication is judged by the satisfaction of certain pragmatic meta-principles that a good explicatum has to satisfy, i.e. the desiderata. In this section, I show how many readings of explication desiderata that have been proposed in the literature can be made precise in terms of geometrical or topological constraints on the conceptual spaces representations of the two concepts, on their conceptual space(s), and on the transition from the (representation of the) explicandum to the (representation of the) explicatum. I also show how the richness of conceptual spaces representation of concepts allows us more fine-grained readings of some desiderata that a good explicatum has to satisfy.

As I will show in Sect. 5, applying this meta-theoretical explication of ‘explication’ to a given case of explication is then a three-step procedure. First, one needs to represent the explicandum and the explicatum in conceptual spaces. Then, one needs to choose one’s favorite reading of explication desiderata. Finally, the adequacy of the explication can be mathematically assessed. The first two steps of this applicability make use of Assumptions 1 and 2 (see Sect. 1). These two assumptions guarantee that both the explicandum and the explicatum are representable in conceptual spaces, that (if needed) there exists a suitable way of mapping the elements of the first conceptual space onto the elements of the second, and that, in assessing the adequacy of the given explication, all the desiderata are understood as strictly-conceptual ones.

Before getting started, let me stress that in what follows I use conceptual spaces theory with a somewhat deflationary caution. Gärdenfors, as I already mentioned, conjoins conceptual spaces with a strong cognitivist view of concepts and properties, together with a lot of other semantical and epistemological claims. Instead, even though I take conceptual spaces to be a fine-grained reliable tool of conceptual representation, I want to remain neutral in this work about which kind of entities concepts are. The use of a geometric representation of concepts is fundamental for my proposal, but I assign no ontological or metaphysical weight to my use of conceptual spaces, using them just as a tool for concept representation.

Then, let the ExplicanDum be a given concept (in the intuitive sense of the term), represented in a conceptual space $CS_{ED}$ by a certain concept (in the technical sense of conceptual spaces teory) $C_{ED} = \{ r_{ED_{1}}, \ldots , r_{ED_{k}} \}$. Assume also that any region $r_{ED_{i}}$ of the concept is obtained from a prototypical region $pr_{ED_{i}}$.⁸ Similarly, let the ExplicaTum be represented in a conceptual space $CS_{ET}$ by a certain concept $C_{ET} = \{ r_{ET_{1}}, \ldots , r_{ET_{t}} \}$. Any given region $r_{ET_{j}}$ of the concept is then obtained from a prototypical region $pr_{ET_{j}}$. Note that in the definitions we have not required that the explicandum and the explicatum are represented in the same conceptual space. As a matter of fact, I will argue that often it is not the case. In order to make precise many explication desiderata we will need a mapping from the elements of $CS_{ED}$ to the elements of $CS_{ET}$. Assumption 1 (see again Sect. 1) guarantees the existence of such an adequate mapping, call it $\phi$ $(\phi : CS_{ED} \rightarrow CS_{ET} )$.⁹

In order to structure more clearly this section, I will use for every reading of a desideratum the following format. First, when it is needed, I will informally discuss the desideratum and the strategy for representing it in conceptual spaces, then I will give the informal norm behind the desideratum. Then, I will draw a picture of a two-dimensional toy-case of an explicandum and/or an explicatum represented in conceptual spaces in order to show how the desideratum can be understood in conceptual spaces. Finally, as promised, I will present a formalized version of the desideratum. Consider, then, the following representation of explication desiderata in conceptual spaces theory.

4.1 Similarity

(S1) Clear-cut extension preservation (Hanna).

Hanna requires the explicatum to preserve the clear-cut extension of the explicandum. In conceptual spaces, the clear-cut extension of a possibly vague concept is given by all the collated polygons (the notion mirroring the super-truth of supervaluationism) associated with its regions. We can then see in the toy-example below (Fig. 3) how the explicatum preserves the clear-cut extension and the anti-extension of the explicandum while deciding part of its borderline region. Since I will use the same format for all the toy-pictures in this section, here is a little guide for understanding them: in a given picture, the inner-polygon represents the clear extension of a concept, the outer polygon (when is present) represents the borderline region of that concept, the rest of the space is the anti-extension of the concept; for simplicity, in these toy-cases I always assume that the explicandum and the explicatum live in the same conceptual space, namely the two-dimensional one represented by the pictures.

Norm: The clear-cut extension of the explicandum ought to be preserved by the explicatum.

Fig. 3

The explicatum (b) preserves the clear-cut extension (the inner-polygon) and the anti-extension (what is not in the outer polygon) of the explicandum (a), while deciding the borderline cases (what is in the outer polygon, but not in the inner one)

Formalization: For the simple case in which the set of elements of $CS_{ED}$ is a subset of the one of $CS_{ET}$, the requirement is simply: $\forall a, \forall i, \exists j: a \in {\underline{u}} (r_{ED_{i}}) \rightarrow a \in {\underline{u}} (r_{ET_{j}})$ and $a \notin {\overline{u}} (r_{ED_{i}}) \rightarrow a \notin {\overline{u}} (r_{ET_{j}})$.

For the general case, in which we do not assume this relation between the base sets of the two spaces, we have to rely on the mapping $\phi$: $\forall a, \forall i, \exists j: a \in {\underline{u}} (r_{ED_{i}}) \rightarrow \phi (a) \in {\underline{u}} (r_{ET_{j}})$ and $a \notin {\overline{u}} (r_{ED_{i}}) \rightarrow \phi (a) \notin {\overline{u}} (r_{ET_{j}})$.

(S2) Favored-contexts preservation (Quine).

Quine’s reading of similarity can be represented in the same way of Hanna’s, relativizing the requirement to favored (i.e. non-deficient) contexts of the explicandum. Assume that a favor context $r_{FC_{ED_{l}}}$ is a subset of one of the regions belonging to the clear-cut extension of the explicandum, i.e. $FC_{ED} = \{ r_{FC_{ED_{1}}}, \ldots , r_{FC_{ED_{t}}} \}$ where $\forall l \leqslant k, \exists i: r_{FC_{ED_{l}}} \subseteq r_{ED_{i}}$. We can see, then, in the picture below (Fig. 4) how the explicatum preserves the favored-context and the anti-extension of the explicandum, while changing its non-favored clear-extension and the borderline cases.

Norm: The clear-cut extension of the explicandum in favored contexts ought to be preserved by the explicatum.

Fig. 4

The explicatum (b) preserves the favored contexts (FC) and the anti-extension of the explicandum (a), while changing some parts of its non-favored extension (inner polygon not in FC) and deciding its borderline region

Formalization: For the simple case when the set of elements of $CS_{ED}$ is a subset of the one of $CS_{ET}$: $\forall a,\forall l,\exists j: a \in {\underline{u}} (r_{FC_{ED_{l}}}) \rightarrow a \in {\underline{u}} (r_{ET_{j}})$ and $\forall a, \forall i, \exists j: a \notin {\overline{u}} (r_{ED_{i}}) \rightarrow a \notin {\overline{u}} (r_{ET_{j}})$.

For the general case: $\forall a,\forall l,\exists j: a \in {\underline{u}} (r_{FC_{ED_{l}}}) \rightarrow \phi (a) \in {\underline{u}} (r_{ET_{j}})$ and $\forall a, \forall i, \exists j: a \notin {\overline{u}} (r_{ED_{i}}) \rightarrow \phi (a) \notin {\overline{u}} (r_{ET_{j}})$.

(S3) Extension adjusting + injection (Brun).

Brun’s two-steps reading of similarity requires first that the extension of the freely created mid-level concept (call it explicandum$_{2}$) overlaps with the extension of the original explicandum. Assuming that $\hbox {explicandum} _{2}$ is represented by the concept $C_{ED2} = \{ r_{ED2_{1}}, \ldots , r_{ED2_{j}} \}$, we require the intersection of the collated polygons associated with regions of the two concepts not to be empty (Fig. 5). Then, Brun requires an injection from the extension of this mid-level concept to the one of the explicatum. The most straightforward way of representing this step of the desideratum would be to require an injective mapping f from the set of clear-cut instances of $\hbox {explicandum} _{2}$ to the clear-cut extension of the explicatum (Fig. 5).¹⁰ It is easy to note that this injection requirement is rather trivially satisfied by almost every case of conceptual engineering that one can imagine.¹¹ A possible stronger requirement would be that every mapping from $\hbox {explicandum}_{2}$ to the explicatum be injective.

Norm: A subset of the clear-cut extension of the explicandum must be preserved by the mid-level concept. Furthermore, there ought to be an injection from the extension of this mid-level concept to the extension of the explicatum.

Fig. 5

In a, the $\hbox {explicandum} _{2}$ (ED2) overlaps with the original explicandum (ED). In b there is an example of an explicatum that satisfies the injection requirement of the second step of Brun’s reading of similarity

Formalization: (Step 1) ${\underline{u}} ( r_{ED_{i}}) \bigcap {\underline{u}} (r_{ED2_{i'}}) \ne \emptyset$.

(Step 2) There exists an injective function $f_{inj}$ from ${\underline{u}} (r_{ED2_{i'}})$ to ${\underline{u}} (r_{ET_{j}})$.

(Alternative, stronger, Step 2) All the possible functions f from ${\underline{u}} (r_{ED2_{i'}})$ to ${\underline{u}} (r_{ET_{j}})$ are injective.

(S4) Contextual quasi-isometry

Thanks to the malleability of conceptual spaces and the adoption of a prototypical view of concepts, more fine-grained readings of the similarity desideratum are possible. I would like to propose, as an example, a reading of the similarity requirement which is philosophically particularly interesting. The informal idea behind it is that the similarity requirement is not adequately understood in terms of extension or intension, but should be modeled instead as the preservation of the large-scale conceptual structure of the explicandum. Under this reading, the explicator can thus change quite freely single instances of the explicandum, but she ought to preserve its general conceptual structure. In order to make precise this idea of large-scale structure preservation, I am going to use the concept of quasi-isometry (Bridson 2008, pp. 443–444). A function f from one metric space $(M_{1}, d_{1})$ to another metric space $(M_{2}, d_{2})$ is called a quasi-isometry, let us write $f_{QI}$, if there exist constants $A \geqslant 1, B\geqslant 0, C\geqslant 0$ such that:

• (1) $\forall x,y \in M_{1}: \frac{1}{A} d_{1}(x,y) - B \leqslant d_{2}(f(x), f(y)) \leqslant A d_{1}(x,y) + B$

• (2) $\forall z \in M_{2}, \exists x\in M_{1}: d_{2} (z, f(x)) \leqslant C$.

Informally, condition 1 tells us that the second metric space is allowed to distort sufficiently large distances by (at most) a constant factor, while condition 2 instead consists of a sort of ‘quasi-surjection’, i.e. it tells us that every element of the second metric space is close to the image of an element of the first one. We can, then, make precise this idea of large-scale preservation by imposing some contextual restrictions on the three constants used in the weak-inequalities of the quasi-isometry. We can, for instance, restrict the constants relative to the diameter $diam (X) : sup \{ d(x,y) : x,y \in X \}$, i.e. the maximal distance between two elements of a metrical spaces, of the related conceptual spaces. The intuitive idea behind this restriction is that the explicatum should not distort too much the conceptual structure of the explicandum, where too much is cashed out in terms of the diameter of the conceptual spaces where the two concepts are represented.¹²

Norm: The large-scale conceptual structure of the extension of the explicandum ought to be preserved (Fig. 6).

Fig. 6

The explicatum (a) distorts the space of the explicandum (b), while preserving its large-scale conceptual structure

Formalization: There exists a quasi-isometric function $f_{QI}$ from $CS_{ED}$ to $CS_{ET}$ with $A + B \le sup \{ diam (CS_{ED}), diam (CS_{ET}) \}$ and $C \le diam (CS_{ET})$.

4.2 Fruitfulness

As we have seen in Sect. 2, the fruitfulness of a given explicatum is often understood in terms of generalization power and connections with other parts of science and philosophy. Under this reading fruitfulness is not a strictly-conceptual desideratum and therefore an explication of its possible readings is outside the scope of the present proposal. That said, I believe that it is possible to propose some strictly-conceptual readings of fruitfulness, looking at some characteristics of the representation of the concept by means of conceptual spaces that make an explicatum a good candidate for being a fruitful notion.

(F1) Convexity

The main idea is to use Gärdenfors’ “criterion P” for natural properties as a normative and theoretical benchmark of (alleged) fruitfulness. Both from a point of cognitive fruitfulness, in the sense of Dutilh Novaes and Reck, and of general conceptual fruitfulness, it seems natural to take as good candidates for fruitfulness concepts the conceptual structure of which resembles the one of our natural concepts. After all, if one takes the engineering metaphor seriously, to require the explicatum to have a conceptual space similar to the ones of natural concepts is just like to require user-friendly products to engineers. We can then require the regions composing the extension of our explicatum to be convex.

Norm: The conceptual-structure of the explicatum ought to resemble the one of our natural concepts (Fig. 7).

Fig. 7

A non-convex (a) and a convex (b) explicatum

Formalization: $\forall x,y \in {\underline{u}}(r_{ET_{j}}), \forall z: \, B(x,z,y) \rightarrow z \in {\underline{u}}(r_{ET_{j}})$.

(F2) Star-shapedness relative to a prototype region

As mentioned earlier in Sect. 3, there are various reasons for thinking that convexity is too strong as a criterion for natural concept. Thus, one may also want to have a weaker geometrical reading of fruitfulness. The concept of star-shapedness relative to a point p, i.e. convexity relative to a given point, seems to share many attractive feature of convexity without imposing so many restrictions on the underling structure of the space (Hernández-Conde 2017). We can then require the regions of the explicatum to be star-shaped relative to the prototypes of the concept. Since arguably the explicatum can also have boundaries which are not sharp and thus have not a unique prototype, it seems natural to define the star-shapedness requirement in relation to the set of prototypical instances of the explicatum, i.e. $pr_{ET_{j}}$.

Norm: The conceptual structure of the explicatum ought to resemble the one of our natural concepts (Fig. 8).

Fig. 8

A non-star-shaped (a) and a star-shaped (b) explicatum

Formalization: $\forall x \in {\underline{u}}(r_{ET_{j}}), \forall y \in pr_{ET_{j}}, \forall z: B (x,z,y) \rightarrow z \in {\underline{u}}(r_{ET_{j}})$.

(F3) Connectedness

Another, even weaker alternative to convexity that has been discussed in the debate over the right naturalness criterion in conceptual spaces is connectedness (Mormann 1993). We can then use it as another possible reading of fruitfulness, by imposing it as a requirement for the regions of the explicatum.

Norm: The conceptual structure of the explicatum ought to resemble the one of our natural concepts (Fig. 9).

Fig. 9

A non-connected (a) and a connected (b) explicatum

Formalization: $\forall j, \forall s,t: (s \cup t = {\underline{u}} (r_{ET_{j}}) \rightarrow C (s,t))$.

4.3 Exactness

(E1) Clear extension (Hanna).

A concept with a clear extension is a concept that does not have any boundary case, i.e. without what we have called boundary regions. Thus, we can easily make precise this reading of the exactness desideratum by requiring the boundary region(s) of the explicatum to be empty.

Norm: The explicatum ought to have a sharp extension with no borderline cases (Fig. 10).

Fig. 10

A non-sharp (a) and a sharp (b) explicatum

Formalization: $\forall j: {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}}) = \emptyset$.

(E2) Vagueness reduction

Similarly, a concept is less vague than another one when the first has fewer boundary cases than the latter. For the simple case in which the explicatum is sufficiently similar (i.e. it has the same clear-cut extension) to the explicandum, we can define this requirement in a qualitative way, requiring the boundary regions of the explicatum to be a proper subset of the ones of the explicandum. However, the explicatum, according to various liberal readings of the similarity requirement, can change even the clear-cut extension of the explicandum. Thus, in the general case, we need a quantitative way of comparing the vagueness of the two concepts. What we need is to add a proper measure to the conceptual spaces of the two concepts, thereby technically making them two measure spaces. Of course, according to the peculiarities of the given conceptual spaces, one has to choose an adequate measure. Generally speaking, assuming a non-negative measure $\mu$ on both the conceptual space of the explicandum and the one of the explicatum, we require the measure of the boundary regions of the explicandum to be strictly bigger than the one of the boundary regions of the explicatum.

Norm: The explicatum ought to be less vague than the explicandum (Fig. 11).

Fig. 11

The explicatum (b) has a smaller boundary region than the explicandum (a) and it is therefore less vague

Formalization: (simple case) $\forall i, \exists j: {\overline{u}} (r_{ED_{i}}) {\setminus } {\underline{u}} (r_{ED_{i}}) \supset {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}})$.

(general case)

$\mu ( \{ {\overline{u}} (r_{ED_{i}}) {\setminus } {\underline{u}} (r_{ED_{i}}) | 1 \leqslant i \leqslant k \} ) > \mu ( \{ {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}}) | 1 \leqslant j \leqslant t \})$.

(E3) No addition of vagueness

If one wants, following Brun, to read the exactness desideratum as the requirement for the explicatum to be not vaguer than the explicandum, it suffices to weaken the precedent desideratum in the obvious way.

Norm: The explicatum ought not to be vaguer than the explicandum (Fig. 12).

Fig. 12

The boundary region of the explicatum (b) has the same size as the region of the explicandum (a), thereby making the explicatum at most as vague as the explicandum

Formalization: (simple case) $\forall i, \exists j: {\overline{u}} (r_{ED_{i}}) {\setminus } {\underline{u}} (r_{ED_{i}}) \supseteq {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}})$.

(general case)

$\mu ( \{ {\overline{u}} (r_{ED_{i}}) {\setminus } {\underline{u}} (r_{ED_{i}}) | 1 \leqslant i \leqslant k \} ) \geqslant \mu ( \{ {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}}) | 1 \leqslant j \leqslant t \})$.

4.4 Simplicity and Other Desiderata

Simplicity, like fruitfulness, seems prima facie a desideratum that cannot arguably be expressed in terms of intrinsic relations amongst the concepts used in the explication, i.e. not a strictly-conceptual desideratum. It could be clarified in terms of the simplicity of the syntax of the target theory in which the explicatum is defined or perhaps in terms of parsimony of new formal tools (i.e. cognitive simplicity for scientists or philosophers). Either way, these readings cannot be made precise with the help of conceptual spaces theory alone. Nevertheless, as in the case of fruitfulness, the structure of the conceptual space of the explicatum can indicate the simplicity of that concept and thus allow for a strictly-conceptual reading of this desideratum.

Furthermore, I will present two other possible desiderata that a good explicatum has to satisfy in conceptual spaces theory. Intuitively, it seems natural to require that the conceptual offspring of a good explication must tell us something more than what was contained in the original explicandum. Two ways in which this aspect of the novelty of the explicatum can be made precise are the extension or preservation of the conceptual scope and the augmentation of discrimination power.

(O1) Simplicity

As we have seen in Sect. 3, a concept is represented in conceptual spaces theory as a set of regions and each one of these regions has a certain shape. Similarly to the case of fruitfulness, one can take the simplicity of the regions of a given explicatum as a sign for its overall conceptual simplicity (as a kind of cognitive economy notion). A simple idea is to count the minimum number of points that are needed to draw the polyhedron $\pi _{i}$ the surface of which is (sufficiently) close to the surface of a given region $r_{ET_{j}}$, obtaining a positive natural number $\sigma$ that we can call the simplicity coefficient of a region.¹³

We can calculate the simplicity coefficient of a given concept $C = \{ r_{1}, \ldots , r_{n} \}$, by calculating the medium coefficient of its regions:

$\sigma (C) = \frac{\sigma (r_{1}), \ldots , \sigma (r_{n})}{n}$. Then, assuming that we have a set of n different explicata $\{ ET, ET_{1}, \ldots , ET_{n} \}$ such that everyone of them equally satisfies the other (more important) desiderata, we can require our explicatum ET to be the one with the smallest simplicity coefficient (Fig. 13).

Norm: Being all the other desiderata equally satisfied, the explicator ought to choose the simplest explicatum.

Fig. 13

Amongst these explicata, our explicator ought to choose $ET_{1}$

Formalization: $\forall x: ET_{x} \in \{ ET, ET_{1}, \ldots , ET_{n} \} \rightarrow \sigma (ET) \leqslant \sigma (ET_{x})$.

(O2) Scope extension

Menger stressed that a good explicatum has to be applicable to new cases, thereby having a wider scope than the original explicandum. We can then make this idea precise by requiring the set of clear-cut instances of the explicatum to be strictly bigger than the one of the explicandum, using the same tools that we used for the vagueness-reduction requirement.

Norm: The scope of the explicandum ought to be extended by the explicatum (Fig. 14).

Fig. 14

The clear-cut extension of the explicatum (b) is bigger than the one of the explicandum (a)

Formalization: (simple case) $\forall i, \exists j : {\underline{u}} (r_{ED_{i}}) \subset {\underline{u}} (r_{ET_{j}})$

(general case) $\mu ( \{ {\underline{u}} (r_{ED_{i}}) | 1 \leqslant i \leqslant k \}) < \mu ( \{ {\underline{u}} (r_{ET_{j}}) | 1 \leqslant j \leqslant t \} )$

(O3)Scope preservation

Just like for the vagueness-reduction case, we can also weaken the scope extension requirement in the following way.

Norm: The scope of the explicandum ought to be preserved by the explicatum (Fig. 15).

Fig. 15

The clear-cut extension of the explicatum (b) has the same size than the one of the explicandum (a)

Formalization: (simple case) $\forall i, \exists j: {\underline{u}} (r_{ED_{i}}) \subseteq {\underline{u}} (r_{ET_{j}})$.

(general case) $\mu ( \{ {\underline{u}} (r_{ED_{i}}) | 1 \leqslant i \leqslant k \}) \leqslant \mu ( \{ {\underline{u}} (r_{ET_{j}}) | 1 \leqslant j \leqslant t \} )$.

(O4) Further discrimination power

Another way in which we can cash-out Menger’s idea of novelty is the augmentation of discrimination power. Our engineered conceptual tools must chart the world in a more fine-grained way than their intuitive ancestors. Conceptual spaces offer a natural way of making this idea precise in terms of the similarity function of a given metric space. Since similarity is an exponentially decaying function of distance, the augmentation of discriminatory power implies a weakening of object similarity from the explicandum to the explicatum. Relying on our mapping $\phi$, we can then require the similarity between two given objects in the conceptual space of the explicandum to be bigger than the one between their images in the conceptual space of the explicatum.

Norm: The explicatum ought to have a more fine-grained conceptual structure than the explicandum (Fig. 16).

Fig. 16

The distances in the space of the explicatum (b) are bigger than the ones in the space of the explicandum (a)

Formalization: $\forall x,y \in CS_{ED}: s^{ED}_{ab} > s^{ET}_{\phi (a)\phi (b)}$.

4.5 Single-Explicatum Explications and Replies to Recent Critiques of Explication

Now that we have seen multiple examples of different readings of desiderata represented by means of conceptual spaces theory, it is easy to picture various ways of adding them together, thereby creating possible explications of ‘explication’ in the single-explicatum sense. Generally speaking, any consistent way of mixing these (readings of) desiderata holds a formal explicatum of a particular reading of explication. As stated in Sect. 2, the aim of this paper is to explicate ‘explication’ in the meta-theoretical sense, giving a bridge-theory that allows a more precise judgment of explication adequacy. In what follows, I will give a couple of examples of how different desiderata made precise in my framework can be put together to make specific readings of explication precise. But by no means I am endorsing anyone of these examples as the favored reading of explication desiderata.

An example of single-explicatum explication that can be made precise within my framework is Hanna’s explication of ‘explication’. This specific reading of explication is made precise by putting together the clear-cut extension preservation reading of the similarity desideratum and the clear extension reading of the exactness desideratum:

(Hanna’s explication of ‘explication’) [S1 + E1]:

$\forall a, \forall i, \exists j: a \in {\underline{u}} (r_{ED_{i}}) \rightarrow \phi (a) \in {\underline{u}} (r_{ET_{j}})$ and $a \notin {\overline{u}} (r_{ED_{i}}) \rightarrow \phi (a) \notin {\overline{u}} (r_{ET_{j}})$;

$\forall j: {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}}) = \emptyset$.

As another example, I will add Menger’s scope preservation desideratum to some technically interesting readings of the three more important desiderata that Carnap stated, i.e. the quasi-isometry reading of similarity, the convexity reading of fruitfulness, and the vagueness-reduction reading of exactness:

(CCVS explication of ‘explication’) [S4 + F1 + E2 + O3]:

There exists a quasi-isometric function $f_{QI}$ from $CS_{ED}$ to $CS_{ET}$ with $A + B \le sup \{ diam (CS_{ED}), diam (CS_{ET}) \}$ and $C \le diam (CS_{ET})$;

$\forall x,y \in {\underline{u}}(r_{ET_{j}}), \forall z: \, B(x,z,y) \rightarrow z \in {\underline{u}}(r_{ET_{j}})$;

$\mu ( \{ {\overline{u}} (r_{ED_{i}}) {\setminus } {\underline{u}} (r_{ED_{i}}) | 1 \leqslant i \leqslant k \} ) > \mu ( \{ {\overline{u}} (r_{ET_{j}}) {\setminus } {\underline{u}} (r_{ET_{j}}) | 1 \leqslant j \leqslant t \})$;

$\mu ( \{ {\underline{u}} (r_{ED_{i}}) | 1 \leqslant i \leqslant k \}) \leqslant \mu ( \{ {\underline{u}} (r_{ET_{j}}) | 1 \leqslant j \leqslant t \} )$.

This explication of ‘explication’ in the single explicatum sense shows how using conceptual spaces theory allows us to understand explication desiderata in a more fine-grained way. All the readings of the different desiderata make use of the richness of conceptual space representation of concepts. This CCVS explication is also truly Carnapian in spirit: the similarity and exactness desiderata pose liberal but precise constraints on the large-scale conceptual structure of the explicandum and the explicatum, while the fruitfulness and the scope extension require the explicatum to show specific improvements in its extension.

The CCVS explication exemplifies how more fine-grained readings of explication desiderata are able to account for certain (alleged) problems of Carnapian explication as a general methodology for conceptual engineering. Take, for instance, the alleged inherent paradoxical tension between similarity and fruitfulness recently stressed by Dutilh Novaes and Reck, i.e. what they call the paradox of adequate formalization (Dutilh Novaes and Reck 2017, pp. 211–213). The similarity requirement in the CCVS explication is spelled out as a large-scale constraint on the conceptual structures of the explicandum and the explicatum. Fruitfulness is instead understood as a specific constraint on the conceptual parts of the explicatum. There is no tension whatsoever between these readings of these two desiderata, namely because they have different scopes. If, in fact, the quasi-isometry between the two conceptual spaces requires the explicatum to preserve the large-scale conceptual structure of the explicandum, the convexity requirement calls for a sharpening of the extension of the explicatum. It is true that the explicator has at the same time to carefully preserve the structure of the explicandum and to craft the explicatum to be as fruitful as possible, but that does not mean that this effort is paradoxical. The key to solve this alleged paradox is then to acknowledge that explication is a very fine-grained procedure of conceptual engineering and that the similarity that explication requires between the explicandum and the explicatum is not really about single conceptual instances but it focuses instead on the more general conceptual structure of the concept. Thus, the CCVS explication shows how the geometrical representation of concepts allows us to capture both the large scale and the small-scale structure of the explicandum and the explicatum, thereby giving us the tools to overcome this apparent tension between these two desiderata.

On a more general note, the meta-theoretical explication of ‘explication’ here proposed can be used to defend explication against the other recent critiques that we have discussed in Sect. 2. By meta-theoretically explicating ‘explication’ we are able to make our external discussions on the adequacy of a given explicatum more precise and clear. Thanks to this meta-conceptual engineering we are thus able to have liberal readings of explication desiderata, such as the quasi-isometry reading of similarity, without giving up rigor on the pragmatic altar. This amounts to a way out for the explicator from the impasse described by Reck of having to choose between an implausible strictly rigorous explication and a not-very-Carnapian pragmatic and liberal explication. Moreover, conceptual spaces, thanks to their malleability and their very detailed representation of concepts, seem also a promising tool for modeling any dialectical and multi-conceptual desideratum version of explication desiderata, thereby offering a solution to the limitations of the received view of explication stressed by Brun.

5 Two Case-Studies: Temperature and Fish

In order to make my framework clearer, I will show how two paradigmatic examples of successful explication can be represented in my framework and can be shown to satisfy the four different desiderata of the CCVS explication. Again, let me stress one more time that I do not endorse this particular reading of explication desiderata as the correct one. It should be understood just as an example of the applicability of my proposal. For historical pleasure, I will use as case-studies Carnap’s examples in (Carnap 1950): the scientific concept of temperature and the morphological concept of fish.

5.1 Temperature

Let me start with the scientific concept of temperature, seen as an explicatum of our ordinary concepts of warm and cold.¹⁴

Let us assume, following Carnap, that our intuitive way of talking about temperature uses classificatory concepts like warm and cold, together with the related intuitive comparative concepts ‘warmer than’ and ‘colder than’, intuitively understood as ‘object a is warmer/colder than object b iff a is perceptually judged warmer/colder than b’. In order to build a conceptual space for these concepts, we will construct perceptive judgments out of a fictional toy-experiment. Assume that a person is asked to compare the warmth of ten buckets of water (alphabetically labeled from a to j), by dipping her arms into two buckets at a time and then judging whether the water contained in one bucket is warmer than the one in the other. Let us assume that, after many of these trials, we can organize the results in the following diagram:

We can read the diagram upwards as a partial order from the coldest sample of water e to the warmest h, with two couples of incomparable buckets (d, a) and (c, i) for which the person’s intuitive judgment was not accurate enough to feel any significant difference in the temperature of the water and thus to discriminate them. We can easily represent this diagram as a simple one-dimensional conceptual space $M_{1}=\{ E_{1}, \delta _{1} \}$ where $E_{1}=\{ a, b, c, d, e, f, g, h, i, j \}$ is the set of elements and $\delta _{1}$ is a non-standard graph-theory-like simple metric on the diagram that counts every bottom-up step between two nodes of the graph.¹⁵ Hence, for instance, $\delta _{1} (e,d)= 1$ because from node e to node d there is only one step, while instead $\delta _{1} (a,j) = 4$. Note that only bottom-up steps are taken into consideration and thus this metric assigns 0 to the two couples of nodes (a, d) and (c, i) , thereby technically mapping them in the same way and signaling that we cannot perceptually discriminate between them. We can define our concept of ‘warmer than’ in terms of distance from node e: for all $x,y\in E_{1}$ we say that x is warmer than y iff $\delta _{1} (e,x) > \delta _{1} (e,y)$. Conversely, we can define x is colder than y iff y is warmer than x.

Assume now that the person in the experiment is asked to classify the ten buckets of water using four different categorical concepts: cold, tepid, warm, hot. Assume that the person’s judgments are as follows: e is cold; f is tepid; b and j are warm; g and h are hot. Two couples of samples are not categorically judged by the person in the experiment, due to her impossibility to decide to which categorical concept they belong: a and d are both cold and tepid, c and i are both tepid and warm. Then, in the same conceptual space we can easily define also these four intuitive categorical concepts. We can use e, f, b, h as prototypical instances, respectively, of cold, tepid, warm, and hot. Our concepts are then defined in terms of distance to the related prototype, thus tessellating our conceptual space. Let us define for all $x \in E_{1}$ the concept cold C(x) iff $\forall y\in \{ e,f,b,h \}: \delta _{1} (e,x) \leqslant \delta _{1} (y,x)$. Hence, it follows that $C = \{e, a, d \}$. In the same way, we define the concepts tepid Te(x) , warm W(x) , and hot H(x) relative respectively to the prototype f, b, h. Note that these definitions respect all the intuitive judgments of the person in the experiment and make the two couples a, d and c, i borderline cases of (respectively) the couples of concepts cold-tepid and tepid-warm, just as we wanted. These four categorical concepts, together with the two comparative concepts previously defined, are then our explicanda.

As our explicata, we can take the comparative concepts derived from the Celsius scale and the Kelvin scale of temperature. Following Stevens’ theory of scales of measurement (Stevens 1946), the Celsius scale is an example of an interval scale, while the Kelvin scale is a ratio scale. Interval scales are unique up to all linear transformations, a fact which makes the zero point just a matter of convention, i.e. we can add to it any constant whatsoever without changing the scale. Ratio scales, instead, are unique only up to multiplication, which implies that they have an actual zero point as the absolute zero of Kelvin scale exemplifies. Technically, in theory of measurement, the scales are defined in terms of groups of transformations of relational structures. Interval scales are isomorphic to a real structure $\langle {\mathbb {R}}^{+}, \ge \rangle$ whose automorphisms are the affine group: $x \rightarrow rx+s$ $r>0$ (Tversky et al. 1971-1989-1990, Volume 3, pp. 115–126). We can then straightforwardly represent a subset of this scale in a one-dimensional conceptual space $M_{2}= \{ E_{2}, \delta _{2} \}$, where $E_{2} = \{ o, a, b, c, d, e, f, g, h, i, j, \ldots , t \}$ is an extension of $E_{1}$ isomorphic to a subset of $R^{+}$ of 101 elements, totally ordered from o to t.¹⁶ Assigning natural numbers from 0 to 100 to the elements respecting their total order, so that $N(o) = 0$ and $N(t) = 100$, we have the following distance function: $\delta _{2} (x,y) := | N(x) - N(y) |$. We can then assume that o represents the zero point of our scale. We define the temperature of a certain object as the distance between o and its corresponding point in the conceptual space: $\forall x: T(x) := \delta _{2} (o,x)$. Related to this conceptual space, we can also define a pair of comparative concepts $warmer^{\circ }$ and $colder^{\circ }$, defined as binary relations in terms of higher/lower temperature: $\forall x,y \in E_{2}$ $warmer^{\circ } (x,y)$ and $colder^{\circ } (y,x)$ iff $T(x) > T(y)$.

Then, going back to our toy-experiment, assume that we measure with a celsius-thermometer the temperature of the water contained in each bucket and that this measurement holds the following results: $T(e) = 10^{\circ }, T(d) = 15^{\circ }, T(a) = 16^{\circ }, T(f) = 25^{\circ }, T(c) = 34^{\circ }, T(i) = 35^{\circ }, T(b) = 50^{\circ }, T(j) = 61^{\circ }, T(g) = 68^{\circ }, T(h) = 80^{\circ }$. We can then represent these judgments in the conceptual space of our explicata, in terms of temperature related to our zero-point o :

Of course, we can also tessellate this space with categorical concepts, thereby offering explicata for our four categorical explicanda. We can then define for all $x\in E_{2}$ the concepts $C^{\circ } (x)$ iff $T(x) < 20$, $Te^{\circ } (x)$ iff $20 \leqslant T(x) \leqslant 40$, $W^{\circ } (x)$ iff $40 < T(x) \leqslant 65$ , and $H^{\circ } (x)$ iff $T(x) > 65$.

We can now assess the adequacy of our explicata, showing how the different desiderata of the CCVS reading of explication are satisfied. Remember that we have four desiderata that our explication has to satisfy, namely quasi-isometry, convexity, vagueness-reduction, and scope preservation.

In order to fulfill the quasi-isometry requirement we need a function $f: (E_{1}, \delta _{1}) \rightarrow (E_{2}, \delta _{2})$, for which there exist constants $A + B \le sup \{ diam (E_{1}), diam (E_{2}) \}$ and $C \le diam (E_{2})$ such that:

• (1) $\forall x,y \in E_{1}: \frac{1}{A} \delta _{1}(x,y) - B \leqslant \delta _{2}(f(x), f(y)) \leqslant A \delta _{1}(x,y) + B$;

• (2) $\forall z \in E_{2}, \exists x\in E_{1}: \delta _{2} (z, f(x)) \leqslant C$.

The diameter of the conceptual space of our explicanda is $\delta _{1} (e,h) = 7$, while the space of our explicata is $\delta _{2} (o,t) = 100$. We can then choose as our f the function that maps elements of the first conceptual space to the elements in the second conceptual spaces representing the temperature of the related bucket: $f(x) = T(x)$. The first weak-inequality is always satisfied by choosing, for instance, $A = 10$ and $B = 20$: $\forall x,y \in E_{1}: \frac{1}{10} \delta _{1}(x,y) - 20 \leqslant \delta _{2}(f(x), f(y)) \leqslant 10 \delta _{1}(x,y) + 20$. For satisfying the second weak-inequality, we have to put $C = 20$ (considering that the maximal distance between an element of the second space and an image of an element of the first one is the one between t and h, which is equal to 20).

For the convexity desideratum note that $E_{2}$ is isomorphic to a subset of reals and that we have defined T(x) in terms of the order relation between elements of this subset. Thus, we have $\forall x,y,z \in E_{2}$: if B(x, z, y) then $T(x)< T(z) < T(y)$ or $T(y)< T(z) < T(x)$. We can then easily see that all the explicata are represented by convex regions in this conceptual space. For instance, our explicatum of cold, $C^{\circ } (x) := T(x) < 20$, is represented by the region $C^{\circ } = \{o, \ldots , e, \ldots , d, a, \ldots \}$, the elements of which are the first 20 elements of our base set, ordered in terms of distance and therefore of temperature. We then have $\forall x,y \in C^{\circ }, \forall z \in E_{2}: B(x,z,y) \rightarrow z \in C^{\circ }$, as requested. The same holds for the other explicata, as it is shown by picture (b) (Fig. 17).

Fig. 17

Representation of the categorical explicanda (a) and the related categorical explicata (b)

For the last two requirements, we have to split the discussion between categorical and comparative explicata. For our two comparative explicata, we have to look at the two product spaces $E_{1}\times E_{1}$ and $E_{2}\times E_{2}$ in which the comparative explicanda and explicata are defined. For the vagueness-reduction requirement, in the first space we have two pairs of elements for which our explicanda ‘warmer/colder than’ are not defined: ${\overline{u}} (r_{ED}) {\setminus } {\underline{u}} (r_{ED}) = \{ (a,d), (c,i) \}$, because $\delta _{1} (e,a) = \delta _{1} (e,d)$ and $\delta _{1} (e,c) = \delta _{1} (e,i)$. Our explicata are instead sharp, so that we have no equivalent case of vagueness and thus the boundary regions consists only of the empty set: ${\overline{u}} (r_{ET}) {\setminus } {\underline{u}} (r_{ET}) = \{ \emptyset \}$. Then, the requirement is trivially satisfied by noting that the empty set is a subset of the boundary region of the first metric space.

As for the scope-preservation requirement, we just notice that all positive instances of our explicanda, ${\underline{u}} (r_{ED})$, are all positive instances of our explicata, ${\underline{u}} (r_{ET})$, so that we have (for the ‘warmer than’ case):${\underline{u}} (r_{ED}) = \{ (h,g), (h,j), \ldots , (g,j), (g,b), \ldots \} \subset {\underline{u}} (r_{ET}) = \{ (h,g), (h,j), \ldots , (g,j), (g,b), \ldots \}$ . For the case of categorical concepts, these two requirements are similarly satisfied. Take for instance our explicandum cold, C(x) : its clear-cut extension is $\{ e \}$ and its borderline region is $\{ a,d \}$. The extension and the borderline region of the related explicatum cold$^{\circ }$ are, respectively, $\{o, \ldots , e, \ldots , d, a, \ldots \}$ and $\{ \emptyset \}$. We can then notice that the extension of our explicandum is preserved by our explicatum and that the borderline region of our explicatum, i.e. the empty set, is trivially a subset of the borderline region of our explicandum.

We have, thus, seen how the CCVS explication of explication shows how the scientific concept of temperature holds satisfactory explicata for our intuitive categorical and comparative notions of temperature. Conceptual spaces, integrating crucial aspects of measure-theory in their representation of concepts (Zenker 2014, p. 8), make transparent the conceptual advantages of the scientific concept of temperature with respect to its intuitive counterpart. The scientific categorical concepts, in fact, extend the scope of our intuitive way of talking beyond any everyday possible experience, while simultaneously allowing us more fine-grained, quantitative discriminations. A philosophically significant consequence of this improved power of discrimination is that our scientific notion of temperature-indiscriminability is transitive, in contrast to the arguable non-transitivity of our phenomenal one.¹⁷ Furthermore, the scientific concept makes it possible to define on the temperature scale sharp categorical concepts that make our communication effective and precise.

The same desiderata are equally satisfied by the pair of explicata $warmer^{*}$ and $colder^{*}$ (and related categorical concepts), defined in relation to the Kelvin scale in the same way of our six explicata. In addition to them, though, the Kelvin scale allows a further discrimination power and, being a ratio scale, it has the technical advantage of having a smaller class of equivalence and thus to be empirically more testable (Gärdenfors and Zenker 2013, pp. 1049–1050).

5.2 Fish

Let us turn our attention to another example that Carnap gave, namely the scientific concept of fish seen as an explicatum of our intuitive conception of what a fish is.¹⁸ As our explicandum we can take the intuitive concept of fish, understood as “an animal that lives in the water”. As our explicatum we take instead the scientific concept of fish, which we will call (following Carnap) piscis, understood as “an aquatic vertebrate with gills and with limbs in the shape of fins” (Helfman et al. 2009, p. 3).

In order to build a conceptual space for these concepts, let us construct a fictional toy-example. Assume that a person who knows nothing about biology is asked to classify the animals of a (very) small zoo in order to decide whether a given animal is a fish or not. Assume that the zoo contains the following nine animals: a tuna, a whale, a shark, a mudskipper, a fire-salamander, a crocodile, a zebra, a lion, and a hippo. The person is then instructed to observe the animals for a certain period of time, after which she has to decide whether a given animal is a fish, according to our intuitively ecological explicandum. Thus, the person would look at which animals in the zoo live in the water. Assume that, on a scale from 0 (never in the water) to 10 (always in the water), the results are the following: 0 (zebra, lion), 2 (hippo), 4 (crocodile, fire-salamander), 5 (mudskipper), 9 (whale), 10 (tuna, shark) (Fig. 18):

Fig. 18

The conceptual space of the explicandum fish

We can then easily represent this diagram in a one-dimensional conceptual space $M_{1} = \{ E_{1}, \delta _{1} \}$ where $E_{1}= \{ z, l, h, c, f, m, w, t, s \}$ and $\delta _{1} (x,y) = | R(x) - R(y) |$, R(x) being a positive integer from 0 to 10, i.e. the result of the experiment. Thus, for instance, we have $\delta _{1}(z,c) = 4$ and $\delta _{1}(w,m) = 4$. We can then suppose to define the concepts of fish and not-fish using as prototypes t (or s) and z (or l), tessellating therefore the conceptual space in two parts. We then define for all $x \in E_{1}$ the concept fish F(x) iff $\delta _{1} (t,x) \leqslant \delta _{1} (z,x)$ and the concept not-fish NF(x) iff $\delta _{1} (z,x) \leqslant \delta _{1} (t,x)$. Hence, we have $F = \{ w, t, s, m \}$ (whale, tuna, shark, mudskipper) , $NF = \{ z, l, h, c, f, m \}$ (zebra, lion, hippo, crocodile, fire-salamander, mudskipper). The mudskipper (m) is then a borderline case.¹⁹ We thus have a conceptual space representation of our explicandum fish.

We turn now to our explicatum piscis. Returning to our toy-experiment, assume now that the same person is asked to classify the animals in the small zoo according to their morphology. After having collected morphological data, the person has to classify again the animals according to our explicatum. Remember that, in order to qualify as a piscis an animal has to be “an aquatic vertebrate with gills and with limbs in the shape of fins”. Then, two major taxonomic changes naturally present themselves in our toy-experiment: the whale and the mudskipper. The whale, who was a clear-cut case of a fish (living exclusively in the water), is not a piscis but instead it is classified as a mammal. Looking closely at the internal and external morphology of the whale, the person in our experiment realizes that it is completely different from the one exemplified by a paradigmatic fish. Whales, in fact, do not have gills, they have lungs, they reproduce like mammals, and so on. The mudskipper, who instead was a borderline case of fish (due to its ability of spending short periods of time outside the water), it qualifies as a clear instance of piscis, due to its internal morphology. Mudskippers have in fact gills and fins, just like other non-amphibious fishes.

Assume then, that the person in the experiment is asked to judge whether the animals in the zoo are pisces or tetrapods, judging by their morphology. The results of this new classification are the following: Pisces (shark, tuna, mudskipper), Tetrapods (fire-salamander, crocodile, whale, zebra, hippo, lion). We can add another sub-level of classification distinguishing pisces between cartilaginous-fishes (shark) and bony-fishes (tuna,mudskipper) and tetrapods between amphibians (fire-salamander), reptiles (crocodile), and mammals (whale, zebra, hippo, lion):

We can, then, easily read this tree as a conceptual space $M_{2} = \{ E_{2}, \delta _{2} \}$, where $E_{2} = E_{1} = \{ z,l,h,c,f,m,w,t,s \}$ and $\delta _{2}$ is a simple metric that counts the number of nodes of the tree between one element and the other. Thus, for instance, $\delta _{2} (s,t) = 1$, $\delta _{2} (t,m) = 0$, $\delta _{2} (t,f) = 3$, $\delta _{2} (m,w) = 3$. Using as our prototype of a piscis s (or t or m) and as our prototype of a tetrapod z (or any other tetrapod, for what it matters) we can define for all $x\in E_{2}$ our explicatum piscis P(x) iff $\delta _{2} (s,x) < \delta _{1} (z,x)$ and the concept of tetrapod T(x) iff $\delta _{2} (z,x) < \delta _{1} (t,x)$.

We can now, as we did in the temperature example, assess the adequacy of the CCVS explication of ‘explication’ by checking whether the conceptual space representation of this example of explication satisfy all its requirements. The first requirement is the existence of a quasi-isometry between the two metric spaces $M_{1}$ and $M_{2}$: $f_{QI}: (E_{1}, \delta _{1}) \rightarrow (E_{2}, \delta _{2})$ with $A + B \le sup \{ diam (CS_{ED}), diam (CS_{ET}) \}$ and $C \le diam (CS_{ET})$. The diameter of the first conceptual space is $\delta _{1} (z,s) = 10$ and the one of the second space is $\delta _{2} (s,l) = 3$. Considering that the two base sets contain the same elements, the simple trivial mapping $f(x) = x$ would do the trick. For instance, fixing the constants $A = 2$, $B \geqslant 5$ (in order to account for the drastic change of the classification of whales), $C = 0$, the following weak-inequalities always hold:

• (1) $\forall x,y \in E_{1}: \frac{1}{2} \delta _{1}(x,y) - 5 \leqslant \delta _{2}(f(x), f(y)) \leqslant 2 \delta _{1}(x,y) + 5$;

• (2) $\forall z \in E_{2}, \exists x\in E_{1}: \delta _{2} (z, f(x)) \leqslant 0$.

The second requirement is instead the convexity of the region representing our explicatum piscis: $\forall x,y \in P: B(x,z,y) \rightarrow z \in P$. It is easy to see that the region $P = \{ s,t,m \}$ is convex, being it a self-contained part of our taxonomic tree. Our third requirement consists of a reduction of vagueness from the explicandum to the explicatum. In the conceptual space of our explicandum we have only one borderline case: m (mudskipper). In the second conceptual space, our concept piscis has instead sharper boundaries and the set of borderline case is empty. Thus, also the vagueness reduction is satisfied. Finally, our last requirement consists in the explicatum preserving the scope of the explicandum. Being our base sets finite, comparing the number of elements that clearly fall under the two concepts will suffice. We can then see how both the clear-cut extension of the explicandum fish $F = \{ w,t,s \}$ and the extension of the explicatum piscis $P = \{ s,t,m \}$ have three elements, satisfying the scope-preservation requirement.

As in the first case-study, conceptual spaces, in virtue of the measure-theoretic consideration that they incorporate, allow us to see the conceptual improvements of our explicatum in comparison to the intuitive explicandum. The concept piscis allows us to make sharper taxonomic distinctions, offering more objectivity of judgment in comparison to an intuitively ecological concept like fish. Not only the concept piscis allows us a more fruitful reclassification of many instances of the concept fish, such as whales, it also permits more fine-grained discriminations, such as the one between different kinds of pisces. Then, of course, the concept piscis has many other non-strictly-conceptual advantages, such as allowing us more generalizations (thanks to its morphological criteria), extending the scope of the concept to non-observable animals (e.g. fossils, etc.), and so on.

Thus, we have seen how the morphological concept of piscis, despite its re-classification of clear-cut cases of the intuitive concept of fish, satisfy all the desiderata of the CCVS explication. Together with the previous example of the scientific concept of temperature, this example shows how successful explications from the history of science can be represented in conceptual spaces and shown to satisfy all the fine-grained readings of the desiderata grouped in the CCVS explication.

6 Conclusion

Let me recall the main steps of the present work. Analyzing and discussing the various readings of explication desiderata in the related literature, we have seen various ways of clarifying the different readings a good explicatum has to satisfy. Using conceptual spaces as a tool for concept representation, I have then proposed an explication of ‘explication’ in what I have called the meta-theoretical sense. Specifically, I have shown how different strictly-conceptual desiderata can be made precise in terms of topological and geometrical constraints over the conceptual spaces representing the concepts involved in the explication. This proposal allows a more precise understanding of the subtle differences between different readings of explication desiderata, thereby contributing to dissolve a lot of vagueness and ambiguity often contained in philosophical discussions about explication. Moreover, thanks to the richness of the conceptual spaces representation of concepts, it is possible to define more fine-grained desiderata that arguably allow explication to overcome some of its alleged limitations, such as the so-called ‘paradox of adequate formalization’.

After all these steps, one could perhaps ask how satisfactory is this meta-theoretical explication of ‘explication’. We can assess this explication by judging how much it satisfies Carnap’s three main desiderata for an explication: similarity, fruitfulness, and exactness. The two examples of Sect. 5 show how paradigmatic cases of explications are also perfectly satisfactory explications according to the present proposal. It seems, then, that this meta-theoretical explication of ‘explication’ is sufficiently similar to Carnap’s original ideas. My proposal seems also quite fruitful. In fact, we have seen at the end of Sect. 4 how conceptual spaces allow us to have more fine-grained readings of explication desiderata that help us to overcome recent critiques of explication. Moreover, having developed this explication of ‘explication’ within the framework of conceptual spaces, one can arguably expect many fruitful interactions between the present proposals and the various applications of conceptual spaces in science and philosophy. Finally, the exactness of the present proposal is evident in the way in which different strictly-conceptual readings of explication desiderata discussed in the literature can be made (more) precise as geometrical/topological constraints over the conceptual spaces of the explicandum and the explicatum.