Skip to main content
SpringerLink
Log in

Quantum Solitodynamics: Non-linear Wave Mechanics and Pilot-Wave Theory

  • Published:
Foundations of Physics Aims and scope Submit manuscript

Abstract

In 1927 Louis de Broglie proposed an alternative approach to standard quantum mechanics known as the double solution program (DSP) where particles are represented as bunched fields or solitons guided by a base (weaker) wave. DSP evolved as the famous de Broglie-Bohm pilot wave interpretation (PWI) also known as Bohmian mechanics but the general idea to use solitons guided by a base wave to reproduce the dynamics of the PWI was abandoned. Here we propose a nonlinear scalar field theory able to reproduce the PWI for the Schrödinger and Klein–Gordon guiding waves. Our model relies on a relativistic ‘phase harmony’ condition locking the phases of the solitonic particle and the guiding wave. We also discuss an extension of the theory for the N particles cases in presence of entanglement and external (classical) electromagnectic fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

Data Availability Statement: No Data associated in the manuscript.

Notes

  1. In the rest of this article contravariant and covariant vectors \(F^\mu\), \(F_\mu\) are often written in the compact form F to simplify the notations. With this convention the scalar product reads \(A_\mu B^\mu :=AB\).

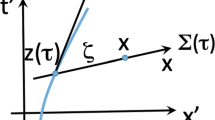
  2. We stress that in order to identify \(\frac{d}{d\tau }\ln {[\mathcal {M}_\Psi (\tau )]}\) and \(\frac{d}{d\tau }\ln {[\mathcal {M}_u(\tau )]}\) we must use \(\mathcal {M}_u(x)\simeq \mathcal {M}_u(z)+ O(\xi )\). The time derivative \(\partial_t\mathcal {M}_u(x)\) computed in the rest frame \(\mathcal {R}_\tau\) includes the derivative of \(O(\xi )\). Using methods developed in Appendix 1 we can indeed justify the condition \(\frac{d}{d\tau }\ln {[\mathcal {M}_\Psi (\tau )]}=\frac{d}{d\tau }\ln {[\mathcal {M}_u(\tau )]}\).

  3. We stress that in order to neglect the self electric energy associated with the electric charge distribution we must have \(\frac{e^2}{a}\ll \frac{b}{\omega_0}=\frac{1}{\omega_0a^2}\), i.e. \(a\ll \frac{(\omega_0)^{-1}}{e^2}\). Moreover, the Sommerfeld structure fine constant \(\alpha =\frac{e^2}{4\pi }\simeq 1/137\) is very small and the previous condition is easy to fulfill for droplet of extension a smaller or equal to the Compton wavelength of the particle \((\omega_0)^{-1}.\)

  4. We note that at the beginning of the present research the author was motivated by an extension of Gueret and Vigier nonlinear equation [42]: \(D^2u=\frac{\Box |u|}{|u|}u-\mathcal {M}_\Psi ^2u\) (in [42] the mass \(\mathcal {M}_\Psi\) was replaced by \(\omega_0\)) that leads directly to the relation \((\partial \varphi +eA)^2=\mathcal {M}_\Psi ^2=(\partial S+ eA)^2\). This implies \(\forall x\) \(\partial S =\partial \phi\), i.e., \(S(x)\equiv \varphi (x)\) (the contact between S and \(\varphi\) is thus stronger than in the phase harmony considered in this work). However, it lets f(x) relatively unconstrained. In fact, from the conservation laws \(\partial [a^2(\partial S+eA)]=0\), \(\partial [f^2(\partial S+eA)]=0\) (with \(S=\varphi\)) we deduce \(v_\psi \partial \log {[f/a]}=0\) meaning that the ratio f/a is constant along a current line. This is a problem since a(x) can increase or decrease and this goes against the notion of a permanent particle (for more on this issue see [19]).

  5. This equation can be derived from the definition \(\mathcal {M}^2_u:=(\partial \varphi +eA)^2\) and by applying the gradient operator \(\partial\) on both sides of the relation.

  6. Compared to the case of Appendix 3 the present model based on Eq. 122 considers an external field associated with the mass \(\mathcal {M}_\Psi (x)\). This explains why we can evade the conclusions obtained with the usual NLKG Eq. 118

  7. We mention that the very interesting models presented recently by Holland [15] and Durt [16] are also proposing an extension for the N-particle case.

  8. Note that we have also \(\delta \tau =\int_0^{t_1} dt_1\sqrt{(1-({\textbf {a}}(0)t_1)^2)}\simeq t_1\)

References

  1. Miller, A.I.: Albert Einstein’s Special Theory of Relativity: Emergence (1905) and Early Interpretations (1905–1911). Springer, New York (1997)

    Google Scholar 

  2. Mie, G.: Grundlagen einer Theorie der Materie. Ann. der Phys. (Berlin) 99, 1–40 (1912)

    Article  MATH  ADS  Google Scholar 

  3. Born, M., Infeld, L.: Foundations of the new field theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 144, 425–451 (1934)

  4. Einstein, A., Rosen, N.: The particle problem in the general theory of relativity. Phys. Rev. 48, 73–77 (1935)

    Article  MATH  ADS  Google Scholar 

  5. Fargue, D.: Permanence of the corpuscular appearance and non linearity of the wave equation. In: Diner, S., et al. (eds.) The Wave-Particle Dualism, pp. 149–172. D. Reidel, Dordrecht (1984)

  6. De Broglie, L.: La mécanique ondulatoire et la structure atomique de la matière et du rayonnement. J. Phys. Radium 8, 225–241 (1927); translated in: de Broglie, L., Brillouin, L.: Selected Papers on Wave Mechanics. Blackie and Son, Glasgow (1928)

  7. De Broglie, L.: Une tentative d’interprétation causale et non linéaire de la mécanique ondulatoire: la théorie de la double solution. Gauthier-Villars, Paris (1956); translated in: de Broglie, L.: Nonlinear Wave Mechanics: A Causal Interpretation. Elsevier, Amsterdam (1960)

  8. Bialynicki-Birula, I., Mycielski, J.: Nonlinear wave mechanics. Ann. Phys. 100, 62–93 (1976)

    Article  MathSciNet  ADS  Google Scholar 

  9. Kiessling, M.K.H.: Quantum Abraham models with de Broglie Bohm laws of electron motion. AIP Conf. Proc. 844, 206 (2006)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  10. Benci, V.: Solitons and Bohmian mechanics, discrete and continuous dynamical systems. Discret. Contin. Dyn. Syst. 8, 303–317 (2002)

  11. Durt, T.: Generalized guidance equation for peaked quantum solitons and effective gravity. EPL 114, 10004 (2016)

    Article  ADS  Google Scholar 

  12. Borghesi, C.: Equivalent quantum equations in a system inspired by bouncing droplets experiments. Found. Phys. 47, 933–958 (2017)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  13. Babin, A., Figotin, A.: Neoclassical Theory of Electromagnetic Interactions. Springer, London (2016)

    Book  MATH  Google Scholar 

  14. Babin, A., Figotin, A.: Wave-corpuscle mechanics for electric charges. J. Stat. Phys. 138, 912–954 (2010)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  15. Holland, P.H.: Uniting the wave and the particle in quantum mechanics. Quant. Stud. Math. Found. 7, 155–178 (2020)

    Article  MathSciNet  Google Scholar 

  16. Durt, T.: Testing de Broglie’s double dolution in the mesoscopic regime. Found. Phys. 53, 2 (2023)

    Article  MATH  ADS  Google Scholar 

  17. Fargue, D.: Louis de Broglie’s “double solution’’, a promising but unfinished theory. Ann. Fond. Broglie 42, 9–18 (2017)

    MathSciNet  Google Scholar 

  18. Collin, S., Durt, T., Willox, R., de Broglie’s, L.: double solution program: 90 years later. Ann. Fond. Broglie 42, 19–70 (2017)

  19. Drezet, A.: The guidance theorem of de Broglie. Ann. Fond. Broglie 46, 65–85 (2021)

    Google Scholar 

  20. Borghesi, C.: Dualité onde-corpuscule formée par une masselotte oscillante dans un milieu élastique : étude théorique et similitudes quantiques. Ann. Fond. Broglie 42, 161–196 (2017)

    MathSciNet  Google Scholar 

  21. Drezet, A., Jamet, P., Bertschy, D., Ralko, A., Poulain, C.: Mechanical analog of quantum bradyons and tachyons. Phys. Rev. E 102, 052206 (2020)

    Article  MathSciNet  ADS  Google Scholar 

  22. Bush, J.W.: The new wave of pilot-wave theory. Phys. Today 68, 47–53 (2015)

    Article  Google Scholar 

  23. Bush, J.W.M.: Pilot-wave hydrodynamics. Annu. Rev. Fluid Mech. 47, 269 (2015)

    Article  MathSciNet  ADS  Google Scholar 

  24. Bush, J.W.M., Oza, A.U.: Hydrodynamic quantum analogs. Rep. Prog. Phys. 84, 017001 (2020)

    Article  MathSciNet  Google Scholar 

  25. Couder, Y., Fort, E.: Single-particle diffraction and interference at a macroscopic scale. Phys. Rev. Lett. 97, 154101 (2006)

    Article  ADS  Google Scholar 

  26. Eddi, A., Fort, E., Moisy, F., Couder, Y.: Unpredictable tunneling of a classical wave-particle association. Phys. Rev. Lett. 102, 240401 (2009)

    Article  ADS  Google Scholar 

  27. Fort, E., Eddi, A., Boudaoud, A., Moukhtar, J., Couder, Y.: Path-memory induced quantization of classical orbits. Proc. Natl Acad. Sci. U.S.A. 107, 17515 (2010)

    Article  ADS  Google Scholar 

  28. Harris, D.M., Moukhtar, J., Fort, E., Couder, Y., Bush, J.W.M.: Wavelike statistics from pilot-wave dynamics in a circular corral. Phys. Rev. E 88, 011001(R) (2013)

    Article  ADS  Google Scholar 

  29. Bacciagaluppi, G., Valentini, A.: Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference. Cambridge University Press, Cambridge (2009)

    Book  MATH  Google Scholar 

  30. Bohm, D.: A suggested interpretation of the quantum theory in terms of “hidden’’ variables. Phys. Rev. 85, 166–179 (1952)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  31. Bohm, D., Hiley, B.J.: The Undivided Universe. Routledge, London (1993)

    MATH  Google Scholar 

  32. Petiau, G.: Sur la représentation des corpuscules en interaction avec des champs extérieurs par des fonctions d’ondes à singularités localisées. C. R. Acad. Sci. (Paris) 239, 344–346 (1954)

    MathSciNet  MATH  Google Scholar 

  33. Petiau, G.: Sur la détermination de fonctions d’ondes à singularités localisées mobiles décrivant des trajectoires circulaires dans le cas d’un potentiel extérieur central. C. R. Acad. Sci. (Paris) 239, 2491–2493 (1955)

    MathSciNet  MATH  Google Scholar 

  34. Petiau, G.: Quelques cas de représentation des corpuscules en intéraction avec des champs extérieurs dans la nouvelle forme de la mécanique ondulatoire (Théorie de la double solution). Séminaire L. de Broglie: Théories Physiques (Paris) 24, exposé 18 (1954–1955)

  35. Roberts, J.: Particule en mouvement dans l’espace et soumise à un champ de force uniforme. Ann. Fond. Broglie 46, 147–167 (2021)

    Google Scholar 

  36. Peyrard, M., Dauxois, T.: Physics of Solitons. Cambridge University Press, Cambridge (2006)

    MATH  Google Scholar 

  37. Born, M.: Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips. Ann. Phys. 30, 1 (1909)

    Article  MATH  ADS  Google Scholar 

  38. Jentzen, R.T., Ruffini, R.: Fermi and electromagnetic mass. Gen. Relativ. Gravit. 44, 2063–2076 (2012)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  39. Poincaré, H.: Sur la dynamique de l’électron. Rend. Circ., Mat. Palermo 21, 129 (1906)

  40. Rosen, G.: Dilatation covariance and exact solutions in local relativistic field theories. Phys. Rev. 183, 1186–1188 (1969)

    Article  ADS  Google Scholar 

  41. Reinisch, G., Fernandez, J.C.: Ehrenfest theorem for nonlinear Klein–Gordon solitary waves. Phys. Rev. Lett. 67, 1968–1970 (1991)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  42. Guerret, P., Vigier, J.P.: De Broglie’s wave particle duality in the stochastic interpretation of quantum mechanics: a testable physical assumption. Found. Phys. 12, 1057–1083 (1982)

    Article  MathSciNet  ADS  Google Scholar 

  43. Dirac, P.A.M., Fock, V.A., Podolsky, B.: On quantum electrodynamics. Phys. Z. Sowjetunion 2, 468 (1932)

    MATH  Google Scholar 

  44. Bell, J.S.: Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  45. Dürr, D., Goldstein, S., Muench-Berndl, K., Zanghì, N.: Hypersurface Bohm–Dirac models. Phys. Rev. A 60, 2729–2736 (1999)

    Article  ADS  Google Scholar 

  46. Fabbri, L.: Spinors in polar form. Eur. Phys. J. Plus 136, 354 (2021)

    Article  Google Scholar 

  47. Fabbri, L.: Weyl and Majorana Spinors as Pure Goldstone Bosons. Adv. Appl. Clifford Algebras 32, 3 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  48. Ruggiero, M.L., Tartaglia, A.: Am. J. Phys. 71, 1303–1313 (2003)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut NEEL, CNRS and Université Grenoble Alpes, 38000, Grenoble, France

    Aurélien Drezet

Authors
  1. Aurélien Drezet
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aurélien Drezet.

Ethics declarations

Competing interests

The author declares no competing interest for this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Drezet, A. Quantum Solitodynamics: Non-linear Wave Mechanics and Pilot-Wave Theory. Found Phys 53, 31 (2023). https://doi.org/10.1007/s10701-023-00671-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10701-023-00671-4

Keywords

Search

Navigation