Skip to main content
SpringerLink
Log in

How do subjects view multiple sources of ambiguity?

  • Published:
Theory and Decision Aims and scope Submit manuscript

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

As illustrated by the famous Ellsberg paradox, many subjects prefer to bet on events with known rather than with unknown probabilities, i.e., they are ambiguity averse. In an experiment, we examine subjects’ choices when there is an additional source of ambiguity, namely, when they do not know how much money they can win. Using a standard assumption on the joint set of priors, we show that ambiguity-averse subjects should continue to strictly prefer the urn with known probabilities. In contrast, our results show that many subjects no longer exhibit such a strict preference.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. This argument can be formalized in the Anscombe and Aumann (1963) setting. See Sarin and Wakker (1992) and Eichberger et al. (2007) for details.

  2. Of course, “winning” here means obtaining the envelope with the equal sign. The subject “wins” in the sense that he or she has correctly guessed the color; while this may mean getting the envelope with the lower payoff.

  3. Anscombe and Aumann (1963) carefully distinguish ex-ante and ex-post randomizations, i.e., whether a randomization decides about which state-contingent act is chosen or whether a randomization determines the outcome in each state after it has been revealed. Most of the modern literature identifies the Anscombe–Aumann approach with ex-post randomizations and uses this interpretation for defining “ambiguity aversion” as a “preference for randomization.” For a critical review of this practice compare the discussion of Sarin and Wakker (1992).

  4. Using a different experimental design Spears (2009) comes to a similar conclusion.

  5. In the actual experiment, we used bags and blue and green marbles. For expositional reasons, we employ the more customary urns, balls, and colors in the text.

  6. Note that indifferent subjects have no strict incentive to mark that they are indifferent. However, there is evidence that subjects have an aversion to lying, in particular in situations in which they have no strategic reason for doing so (cf. Gneezy 2005; Vanberg 2008; and Hurkens and Kartik 2009). Also, as we shall see below in treatment “between,” we change the default option in case of indifference and do not find a significant difference.

  7. The content of envelope \(\ne \) follows by implication.

  8. Bade (2008) provides a discussion of alternative ways for defining independence of sets of priors.

  9. Since payoffs in (1) are linear in probabilities, minimal payoffs are, of course, unaffected by taking the convex hull.

  10. The notion of an unambiguous event is not “unambiguous” in the literature. The notion suggested here corresponds to the concept advanced in Nehring (1999), where further references to this debate can be found.

  11. Note that this condition is automatically satisfied if Assumption 1 and condition (2) hold.

  12. This dummy measures any general tendency to change behavior from the first to the second choice. It is thus related but different from the order effect. The latter cannot simply be assessed with a dummy in this regression because the value of this dummy for subjects in the treatment “between” would be missing (as they only face one situation).

  13. These estimates of the marginal effects for the average participant are very similar to the average marginal effects.

  14. See also Nehring (1999) who shows that this is true even if one of the marginal capacities is additive.

  15. These are the instructions for treatment “within.” The instructions for treatment “between” are modified in an obvious way such that subjects only have to make one choice in one of the situations.

References

  • Anscombe, F. J., & Aumann, R. J. (1963). A definition of subjective probability. Annals of Mathematical Statistics, 34, 199–205.

    Article  Google Scholar 

  • Bade, S. (2008). Stochastic independence with maxmin expected utilities, mimeo, Penn State University.

  • Chateauneuf, A., & Lefort, J-Ph. (2008). Some Fubini theorems on product \(\sigma \)-algebras for non-additive measures. International Journal of Approximate Reasoning, 48, 686–696.

    Article  Google Scholar 

  • Cohen, M., Gilboa, I., Jaffray, J., & Schmeidler, D. (2000). An experimental study of updating ambiguous beliefs. Decision and Policy, 5, 123–133.

    Article  Google Scholar 

  • Cox, J. C., Sadiraj, V. & Schmidt, U. (2011). Paradoxes and mechanisms for choice under risk, Kiel Working Paper No. 1712, University of Kiel.

  • Denneberg, D. (1997). Representation of the Choquet integral with the r-additive Möbius transform. Fuzzy Sets and Systems, 92, 139–156.

    Article  Google Scholar 

  • Dominiak, A., Duersch, P., & Lefort, J-Ph. (2012). A dynamic Ellsberg urn experiment. Games and Economic Behavior, 75, 625–638.

    Article  Google Scholar 

  • Dominiak, A., & Schnedler, W. (2011). Uncertainty aversion and preferences for randomization: An experimental study. Economic Theory, 48(2), 289–312.

    Article  Google Scholar 

  • Eichberger, J., Grant, S., & Kelsey, D. (2007). Updating Choquet beliefs. Journal of Mathematical Economics, 43, 888–899.

    Article  Google Scholar 

  • Eichberger, J., & Kelsey, D. (1996a). Uncertainty aversion and dynamic consistency. International Economic Review, 37, 625–640.

    Article  Google Scholar 

  • Eichberger, J., & Kelsey, D. (1996b). Uncertainty aversion and preference for randomization. Journal of Economic Theory, 71, 31–43.

    Article  Google Scholar 

  • Eliaz, K. & Ortoleva, P. (2012). Multidimensional Ellsberg, mimeo, California Institute of Technology.

  • Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. Quarterly Journal of Economics, 75, 643–669.

    Article  Google Scholar 

  • Epstein, L. G., & Schneider, M. (2003). Recursive multiple-priors. Journal of Economic Theory, 113, 1–31.

    Article  Google Scholar 

  • Ghirardato, P. (1997). On independence for non-additive measures, with a Fubini theorem. Journal of Economic Theory, 73, 261–291.

    Article  Google Scholar 

  • Gilboa, I., & Schmeidler, D. (1989). Maxmin expected utility with non-unique prior. Journal of Mathematical Economics, 18, 141–153.

    Article  Google Scholar 

  • Gneezy, U. (2005). Deception: The role of consequences. American Economic Review, 95(1), 384–394.

    Article  Google Scholar 

  • Hansen, L. P., Sargent, T. J., Turmuhambetova, G. A., & Williams, N. (2006). Robust control and model misspecification. Journal of Economic Theory, 128, 45–90.

    Article  Google Scholar 

  • Hendon, E., Jacobsen, H. J., & Sloth, B. (1996). The product of capacities and belief functions. Mathematical Social Sciences, 32, 95–108.

    Article  Google Scholar 

  • Hurkens, S., & Kartik, N. (2009). Would I lie to you? On social preferences and lying aversion. Experimental Economics, 12, 180–192.

    Article  Google Scholar 

  • Klibanoff, P. (2001). Stochastically independent randomization and uncertainty aversion. Economic Theory, 18, 605–620.

    Article  Google Scholar 

  • Klibanoff, P., Marinacci, M., & Mukerji, S. (2005). A smooth model of decision making under ambiguity. Econometrica, 73, 1849–1892.

    Article  Google Scholar 

  • Nehring, K. (1999). Capacities and probabilistic beliefs: A precarious coexistence. Mathematical Social Sciences, 38, 197–213.

    Article  Google Scholar 

  • Oechssler, J. & Roomets, A. (2013). A test of mechanical ambiguity, mimeo, University of Heidelberg.

  • Raiffa, H. (1961). Risk, ambiguity and the Savage axioms: A comment. Quarterly Journal of Economics, 75, 690–694.

    Article  Google Scholar 

  • Sarin, R. K., & Wakker, P. P. (1992). A simple axiomatization of nonadditive expected utility. Econometrica, 60(6), 1255–1272.

    Article  Google Scholar 

  • Sarin, R. K., & Wakker, P. P. (1998). Dynamic choice and nonexpected utility. Journal of Risk and Uncertainty, 17, 87–119.

    Article  Google Scholar 

  • Schmeidler, D. (1989). Subjective probability and expected utility without additivity. Econometrica, 57, 571–587.

    Article  Google Scholar 

  • Spears, D. (2009). Preference for randomization? Anscombe–Aumann Inconsistency in the Lab, mimeo, Princeton University.

  • Trautmann, Stefan T., & van de Kuilen, Gijs. (2013). Ambiguity attitudes. In Gideon Keren & Wu George (Eds.), Handbook of judgment and decision making. Oxford: Blackwell.

    Google Scholar 

  • Vanberg, C. (2008). Why do people keep their promises? An experimental test of two explanations. Econometrica, 76, 1467–1480.

    Article  Google Scholar 

Download references

Acknowledgments

We thank Adam Dominiak, Peter Dürsch, Paolo Ghirardato, Yoram Halevy, Jean-Philippe Lefort, Christoph Vanberg, Peter Wakker, and participants of the D-TEA workshop in Paris 2011 for spirited discussions. We particularly thank a very attentive referee for many useful comments.

Author information

Authors and Affiliations

  1. University of Heidelberg, Heidelberg, Germany

    Jürgen Eichberger & Jörg Oechssler

  2. University of Paderborn, Paderborn, Germany

    Wendelin Schnedler

Authors
  1. Jürgen Eichberger
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jörg Oechssler
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wendelin Schnedler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jürgen Eichberger.

Additional information

An earlier version of this paper was circulated under the title “How do people cope with an ambiguous situation when it becomes even more ambiguous?”.

Appendix

Appendix

See Table 8.

Table 8 Urns choices in treatments SO and OS
Full size table

1.1 Instructions

Welcome to our experiment. Please read these instructionsFootnote 15 carefully. Turn off your mobile phone, do not talk to your neighbors, and remain quiet throughout the experiment. If you have any questions, please raise your hand, and someone will come to you.

In this experiment, you will make a number of decisions. Make your decisions carefully since you can earn some money, which will be paid in cash at the end of the experiment. The decisions you are supposed to make differ for all participants somewhat. So, copying from your neighbor(s) makes no sense.

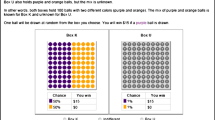
The experimenter has two bags on his table, with each bag containing 40 marbles. Each marble is either blue or green. In Bag, H half of the marbles are green, and the other half are blue. For Bag U you do not know how many marbles are blue and how many are green. That is, any combination is possible for bag U, from 0 blue marbles (that is, 40 green marbles) to 40 blue marbles (that is, 0 green marbles). After completion of the experiment, you are invited to check the content of bag H and bag U.

In total, we have three situations, each of them is associated with two envelopes containing money. In each situation one of the two envelopes contains 1 euro and the other 3 euros. It depends on the situation which of the two envelopes contains 3 euros.

In each of the three situations you specify

  • the bag (U or H) from which to draw a marble

  • the color (blue or green) of the marble

If the marble being drawn has the color you specified, you will get the amount contained in the envelope labeled \(=\). If the marble being drawn has not the color you specified, you will get the amount contained in the envelope labeled \(\ne \).

If you do not care from which bag the ball is drawn or for a particular color, please indicate so. Since it does not matter for you, we will for simplicity take the first bag or first color, respectively.

The marbles will be drawn at the end of the experiment by one of the participants you picked. After each drawing, the marble is put back into the bag.

Situation 1

With a probability unknown to you, it was determined whether the \( = \) envelope or the \(\ne \) envelope contains 3 euros. That is, you do not know whether the \(=\) envelope or the \(\ne \) envelope contains 3 euros.

  • \(\square \) I want the marble to be drawn from bag U

  • \(\square \) I want the marble to be drawn from bag H

  • \(\square \) I don’t care which bag is selected

  • I specify the following color: \(\square \) blue \(\square \) green \(\square \) I don’t care

Situation 2

The \(=\) envelope contains 3 euros and the \(\ne \) envelope contains 1 euro.

  • \(\square \) I want the marble to be drawn from bag U

  • \(\square \) I want the marble to be drawn from bag H

  • \(\square \) I don’t care which bag is selected

  • I specify the following color: \(\square \) blue \(\square \) green \(\square \) I don’t care

Situation 3

At the end of the experiment, a participant will toss a fair coin. If heads wins, 3 euros are put in the \(=\) envelope, and 1 euro in the \(\ne \) envelope. If tails wins, the money is allocated vice versa.

  • \(\square \) I want the marble to be drawn from bag U

  • \(\square \) I want the marble to be drawn from bag H

  • \(\square \) I don’t care which bag is selected

  • I specify the following color: \(\square \) blue \(\square \) green \(\square \) I don’t care

Rights and permissions

Reprints and permissions

About this article

Cite this article

Eichberger, J., Oechssler, J. & Schnedler, W. How do subjects view multiple sources of ambiguity?. Theory Decis 78, 339–356 (2015). https://doi.org/10.1007/s11238-014-9428-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11238-014-9428-1

Keywords

JEL Classification

Search

Navigation