1 Introduction

Traditional computers implement the IEEE 754-1985 binary floating point standard to represent and work with numbers [see IEEE (1985)]. Although computers are able to work with finite numbers, numerical computations that involve infinite and infinitesimal quantities are impossible due to both the presence of indeterminate forms and the impossibility to put the infinite representation of a number in the finite computer memory [see Sergeyev (2017)].

The Infinity Computer is a new kind of a supercomputer that allows one to work numerically with finite, infinite, and infinitesimal numbers. The software simulator of the Infinity Computer was written in the C++ language and is used in several research domains, especially in mathematics and physics to solve difficult real-life problems [see Sergeyev (2017) and references given therein]. Nevertheless, the software simulator is not yet sufficiently mature to address problems in control theory and dynamic systems due to implementative issues related to extending and integrating the C++ source code of the arithmetical and elementary operations in well-known environments like Simulink.

To overcome these issues, the paper presents an innovative solution that allows one to use the Infinity Computer arithmetic within the Simulink environment, which is a well-known graphical programming environment, developed by MathWorks, for studying and analyzing dynamic systems [see Falcone and Garro (2019)]. Simulink provides a graphical block diagramming notation tightly integrated with the Matlab environment. Simulink is widely used in the modeling and simulation domain, including distributed simulation, Co-Simulation of Cyber-Physical Systems (CPS) and Model-Based design [see Bocciarelli et al. (2018); D’Ambrogio et al. (2019); Möller et al. (2016b, (2017)].

The rest of the paper is organized as follows. Section 2 provides an introduction to the Infinity Computer and MATLAB/Simulink concepts and background knowledge on the research domain. Section 3 presents the Simulink-based solution for operating with the Infinity Computing concepts within the Simulink environment. In Sect. 4, three series of numerical experiments are presented to show the feasibility and validity of the solution. Finally, conclusions and future works are delineated in Sect. 5.

2 Background

The paper uses notions and concepts from Infinity Computing and its representation of numbers along with related algebraic operations, and MATLAB/Simulink, as described in the following subsections.

2.1 Infinity computing and representation of numbers

In the Infinity Computing framework [see Sergeyev (2017)], all numbers are represented using the positional numeral system with the infinite radix \({\displaystyle {{\textcircled {1}}}}\) introduced as the number of elements of the set of natural numbers [see, e.g., Sergeyev (2017)]:

$$\begin{aligned} C = d_0 {\displaystyle {{\textcircled {1}}}}^{p_0} + d_1{\displaystyle {{\textcircled {1}}}}^{p_1} + \ldots + d_n {\displaystyle {{\textcircled {1}}}}^{p_n}, \end{aligned}$$
(1)

where quantities \(d_i,~i=0,\ldots ,n\), are finite (positive or negative) floating-point numbers called grossdigits, and \(p_i,~i=0,\ldots ,n\), are called grosspowers and can be finite, infinite and infinitesimal (positive or negative), n is the number of grosspowers used in computations (can be fixed or variable for all computations)Footnote 1. Due to limitations of the Simulink (e.g., difficulties in working with variable-sized matrices in algebraic loops) and for simplicity, only finite floating-point grosspowers are considered in this paper. It should be noted that this methodology is not related to non-standard analysis [see Sergeyev (2019) for details].

One can see that a finite floating-point number A can be easily expressed in this framework using only one grosspower \(p_0 = 0:\) \(A = A{\displaystyle {{\textcircled {1}}}}^{0}\). Moreover, different infinite and infinitesimal numbers can be also expressed: e.g., the numbers \({\displaystyle {{\textcircled {1}}}}\), \({\displaystyle {{\textcircled {1}}}}^{2}\), \(-1.5{\displaystyle {{\textcircled {1}}}}^{2.5}\), \(-1.2{\displaystyle {{\textcircled {1}}}}^{3.2}-1.2{\displaystyle {{\textcircled {1}}}}^{0}+2.3{\displaystyle {{\textcircled {1}}}}^{-1.2}\) are infinite, since they contain at least one finite positive grosspower, while the numbers \({\displaystyle {{\textcircled {1}}}}^{-1} = \frac{1}{{\displaystyle {{\textcircled {1}}}}}\), \(2.5{\displaystyle {{\textcircled {1}}}}^{-1.5}\), \(1.3{\displaystyle {{\textcircled {1}}}}^{-2.2}-1.7{\displaystyle {{\textcircled {1}}}}^{-3.1}\) are infinitesimal, since they contain only finite negative grosspowers. Let us call the numbers expressed in the form (1) as grossnumbers hereinafter.

The Infinity Computer has been already successfully used for solving problems in applied mathematics, e.g., in optimization [see Cococcioni et al. (2020b, (2018); De Cosmis and De Leone (2012); De Leone (2018); De Leone et al. (2018); Gaudioso et al. (2018); Sergeyev et al. (2018)], infinite series [see Zhigljavsky (2012)], game theory and probability [see Calude and Dumitrescu (2020a); Fiaschi and Cococcioni (2018); Rizza (2019)], fractals and cellular automata [see Caldarola (2018); D’Alotto (2015); Sergeyev (2011b, (2016)], numerical differentiation and ordinary differential equations [see Amodio et al. (2016); Falcone et al. (2020b); Iavernaro et al. (2019); Sergeyev (2011a, (2013); Sergeyev et al. (2016)], etc.

2.2 MATLAB/Simulink

Simulink is a software developed by MathWorks as extension of MATLAB [see MathWorks (2019a)]. It allows engineers to rapidly build, simulate and analyze dynamic systems using block diagram notation before moving to hardware. Moreover, Simulink offers a graphical support that shows the progress of a simulation, significantly increasing understanding of the system’s behavior.

The potential productivity improvement achieved with Simulink to programming is impressive [see Falcone and Garro (2019); MathWorks (2019a)]. In the past, the common approach to develop a system was to start from its components by describing their logic through blocks. Then, blocks were translated into the corresponding source code according to a given programming language (e.g., C/C++). This approach involved duplication of effort, since the system had to be described twice; the first time using block notation and then in a programming language. This practice exposed to accuracy risks in the translation process from blocks to source code, making debugging phases difficult because errors could be in the design (block diagram level), in the programming (programming level), and/or in the translation process. With Simulink, this approach is no longer necessary since blocks are the “program”.

Simulink is widely used in research and industry to explore and analyze different design alternatives of complex system in order to find the best configuration that meets the requirements. Research teams can exploit the multi-domain nature of Simulink to collaboratively simulate the behavior of the system’s components, each of which developed by a team, also to understand how components influence the behavior of the entire system Falcone and Garro (2016a); Falcone et al. (2017a, (2017b, (2018a).

Simulink allows one: to reduce expensive prototypes by testing the system in otherwise risky and/or time-consuming conditions; to validate the system design with hardware-in-the-loop testing and rapid prototyping; and to maintain traceability of requirements from design down to the corresponding source code.

3 A simulink-based solution for operating with the infinity computer

This section presents a Simulink-based solution for operating with the Infinity Computing concepts presented in Subsection 2.1. The subsequent subsections are devoted to the presentation of the architecture of the solution and the three functional modules Arithmetic Blocks Module (ABM), Elementary Blocks Module (EBM), Utility Blocks Module (UBM). For each module sets of blocks are described along with examples showing their validity.

3.1 Architecture

The proposed solution brings the power of the Infinity Computer into the Simulink Graphical Programming Environment (GPE). The solution has been designed to facilitate the modeling and simulation of dynamic systems by allowing engineers to focus on the specific aspects of their system’s components, without dealing with the low level functionalities exposed by the Infinity Computer Arithmetic C++ library (ICA-lib).

The presented Simulink-based solution is general-purpose and domain-independent; as a consequence, it can be exploited in all industrial and scientific domains where a high level of accuracy in the calculations represents a mainstay (e.g., Cyber-Physical Systems, Robotics and Automation, Aerospace [see Falcone and Garro (2018); Falcone et al. (2017b); Garro et al. (2015, (2018b)]).

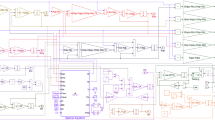
The design and implementation of the solution have been focused on standard software engineering methods and techniques, in particular, on the Agile software development process [see Martin (2002); Venkatesh et al. (2020)]. The solution has been developed through the use of standard Simulink Blocks and S-Functions, which allows engineers to jointly exploit the advantages coming from the Infinity Computer and the already available Simulink functionalities. Figure 1 presents an overview of the Simulink-based Infinity Computing solution and its integration with the MATLAB/Simulink environments.

Fig. 1
figure 1

Overview of the Simulink-based Infinity Computer solution and its integration in the MATLAB/Simulink environment

Full size image

In the following Fig. 1, the Simulink-based solution is placed in the middle of three layers.

The Simulink UI represents the Simulink environment used for modeling, analyzing and simulating dynamic systems through the graphical block diagramming tool according to the Model-Based Design (MBD) paradigm [see Falcone and Garro (2017b)]. MBD offers an efficient approach to address problems associated with the design and implementation of complex systems, signal processing equipment and communication components. This approach provides a common framework where engineers can define models with advanced functionalities using continuous-time and discrete-time blocks. The so-obtained models can be simulated in Simulink by using different operational conditions leading to rapid prototyping, testing and verification of the system’s requirements and performances.

The Simulink Environment layer provides all the standard Simulink blocks along with the ones offered by the Simulink-based Infinity Computer solution (details will be given in Subsection 3.3).

The Matlab Environment represents the Matlab infrastructure where the Infinity Computer arithmetic C++ library (ICA-lib) has been integrated in order to handle infinite, finite, and infinitesimal computations. The integration of the ICA-lib in Simulink has been done by creating a MATLAB executable file (MEX), which provides an interface between the involved parts. When compiled, the MEX file is dynamically loaded by Simulink and permits to invoke the Infinity Computer arithmetic functions as if they were natively built-in.

The ICA-lib offers a set of services, each of which offers some C++ classes and interfaces that implement specific functionalities to handle infinite, finite, and infinitesimal quantities along with related computations.

3.2 Representation of grossnumbers in Simulink

In the Simulink-based solution of the Infinity Computer, a grossnumber x is represented through a standard Simulink Constant block as a variable-sized vector (1-D array) or matrix (2-D array) depending on the dimensionality of the “Constant value” parameter [see MathWorks (2019a)]. Specifically, the output has the same dimensions and elements as the “Constant value” parameter. If “Constant value” is a vector and “Interpret vector parameters as 1-D” is enabled, Simulink treats the output as a 1-D array; otherwise, the output is managed as a matrix (i.e., a 2-D array). Regardless of the output size, the first column represents the grossdigits, whereas the second one defines the grosspowers of a number written in the form (1): the number (1) is represented by the following matrix:

$$\begin{aligned} C = \left[ \begin{matrix} d_0 &{} p_0\\ d_1 &{} p_1 \\ \cdots &{}\\ d_n &{} p_n\end{matrix}\right] . \end{aligned}$$
(2)

For instance, the number 2 is represented in this solution through a vector \(\left[ \begin{matrix} 2&0 \end{matrix}\right] \), while the number \(5{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\) is represented by the matrix \(\left[ \begin{matrix} 5 &{} 0\\ 1 &{} -1 \end{matrix}\right] \).

3.3 Functional blocks

A set of functional blocks have been created to manage computations on infinite, finite, and infinitesimal quantities written in the form (2) that each functional block takes as input infinite, finite, and infinitesimal quantities that are forwarded to the associated S-Function to perform the computation by interacting with ICA-lib. Figure 2 shows the functional block modules that constitute the Simulink-based Infinity Computer solution.

Fig. 2
figure 2

The Simulink-based infinity computer solution with provided functional block modules

Full size image

3.3.1 Arithmetic blocks module

This section is devoted to the Arithmetic Blocks Module (ABM). It provides a set of blocks devoted to perform arithmetic computations on infinite, finite, and infinitesimal quantities, such as Sum, Subtraction, Multiplication and Division.

All the blocks take as input two arguments x, y, which are defined as follow:

$$\begin{aligned} x = \left[ \begin{matrix} x_0 &{} p_0\\ x_1 &{} p_1 \\ \cdots \\ x_N &{} p_N\end{matrix}\right] , y = \left[ \begin{matrix} y_0 &{} q_0\\ y_1 &{} q_1 \\ \cdots \\ y_N &{} q_N\end{matrix}\right] , \end{aligned}$$
(3)

where N is a configuration parameter that represents the maximum precision used to perform operations. This number fixes the number of rows in the matrix representation (2) of each grossnumber (1). It is defined within each block and by default its value is set to 20.

The real precision of the Infinity Computer is defined through the parameter \(n,~n~\le ~N\), which can be configured in the “n_configuration.m” file.

The x, y arguments represent the grossnumbers

$$\begin{aligned} \begin{array}{rcl} x &{}=&{} x_0{\displaystyle {{\textcircled {1}}}}^{p_0}+x_1{\displaystyle {{\textcircled {1}}}}^{p_1} + ... + x_N {\displaystyle {{\textcircled {1}}}}^{p_N},\\ [.3cm] y &{}=&{} y_0{\displaystyle {{\textcircled {1}}}}^{q_0}+y_1{\displaystyle {{\textcircled {1}}}}^{q_1} + ... + y_N {\displaystyle {{\textcircled {1}}}}^{q_N}. \end{array} \end{aligned}$$
(4)

The result of the applied operation is a matrix \(z \in {\mathbb {R}}^{N \times 2} \):

$$\begin{aligned} z = z_0{\displaystyle {{\textcircled {1}}}}^{\gamma _0}+z_1{\displaystyle {{\textcircled {1}}}}^{\gamma _1} + ... + z_N {\displaystyle {{\textcircled {1}}}}^{\gamma _N}, \end{aligned}$$
(5)

where z has dimension and number of elements according to the Infinity Computer algebra [see Sergeyev (2003)], where the first n rows are significant, whereas the other \(N-n\) ones are null.

For each block included in ABM, the specific function and an example that shows its application are presented, hereinafter.

Fig. 3
figure 3

Simulink models that perform addition (a), subtraction (b), multiplication (c), and division (d) of the grossnumbers \(3{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\) and \(1{\displaystyle {{\textcircled {1}}}}^{1}+2{\displaystyle {{\textcircled {1}}}}^{0}+5{\displaystyle {{\textcircled {1}}}}^{-1}\)

Full size image

Sum. This block performs addition on its inputs. The Simulink model shown in Fig. 3a performs the addition of \(A = 3{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\) and \(B = 1{\displaystyle {{\textcircled {1}}}}^{1}+2{\displaystyle {{\textcircled {1}}}}^{0}+5{\displaystyle {{\textcircled {1}}}}^{-1}\). After the Start simulation command is executed, the result \(C = 1{\displaystyle {{\textcircled {1}}}}^{1}+5{\displaystyle {{\textcircled {1}}}}^{0}+6{\displaystyle {{\textcircled {1}}}}^{-1}\) is shown through the standard Display block.

The grossnumbers A, B, and C are defined as:

$$\begin{aligned} A = \sum _{i=1}^{K} a_{k_i}{\displaystyle {{\textcircled {1}}}}^{k_i}, B = \sum _{j=1}^{M} b_{m_j}{\displaystyle {{\textcircled {1}}}}^{m_j}, C = \sum _{i=1}^{L} c_{l_i}{\displaystyle {{\textcircled {1}}}}^{l_i}. \end{aligned}$$
(6)

The result C is defined by including both the items of A, \(a_{k_i}{\displaystyle {{\textcircled {1}}}}^{k_i} : k_i \ne m_j\) with \(1 \le j \le M\) and the ones of B, \(b_{m_j}{\displaystyle {{\textcircled {1}}}}^{m_j} : m_j \ne k_i\) with \(1 \le i \le K\), and the terms having the same grosspower \((a_{l_i}+b_{l_i}){\displaystyle {{\textcircled {1}}}}^{l_i}\), according to the Infinity Computer arithmetic described in Sergeyev (2017).

Subtraction. This block performs subtraction on its grossnumbers in inputs. This operation is a direct consequence of the Sum block above described. Figure 3b shows a Simulink model that performs the subtraction between \(A = 3{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\) and \(B = 1{\displaystyle {{\textcircled {1}}}}^{1}+2{\displaystyle {{\textcircled {1}}}}^{0}+5{\displaystyle {{\textcircled {1}}}}^{-1}\). The result \(C = -1{\displaystyle {{\textcircled {1}}}}^{1}+1{\displaystyle {{\textcircled {1}}}}^{0}-4{\displaystyle {{\textcircled {1}}}}^{-1}\) is shown by using the Display block.

Multiplication. This block performs multiplication on its inputs. Figure 3c shows a Simulink model that carry out the multiplication operation between the grossnumbers \(A = 3{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\) and \(B = 1{\displaystyle {{\textcircled {1}}}}^{1}+2{\displaystyle {{\textcircled {1}}}}^{0}+5{\displaystyle {{\textcircled {1}}}}^{-1}\). The Display block shows the result of the operation \(C = 3{\displaystyle {{\textcircled {1}}}}^{1}+7{\displaystyle {{\textcircled {1}}}}^{0}+17{\displaystyle {{\textcircled {1}}}}^{-1}+5{\displaystyle {{\textcircled {1}}}}^{-2}\) defined as follow:

$$\begin{aligned} C = \sum _{j=1}^{M} C_{j}, \qquad 1 \le j \le M, \end{aligned}$$
(7)

where \(C_j = b_{m_j}{\displaystyle {{\textcircled {1}}}}^{m_j} \cdot A = \sum _{i=1}^{K} a_{k_i}b_{m_j}{\displaystyle {{\textcircled {1}}}}^{k_i+m_j}\).

Division. This block performs division on its inputs. The Simulink model shown in Fig. 3d performs the division operation between the grossnumbers \(A = 3{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\) and \(B = 1{\displaystyle {{\textcircled {1}}}}^{1}+2{\displaystyle {{\textcircled {1}}}}^{0}+5{\displaystyle {{\textcircled {1}}}}^{-1}\). The grossnumber \(C = 3{\displaystyle {{\textcircled {1}}}}^{-1}-5{\displaystyle {{\textcircled {1}}}}^{-2}-5{\displaystyle {{\textcircled {1}}}}^{-3}+35{\displaystyle {{\textcircled {1}}}}^{-4}...\) that is the result of the computation is shown by the Display block.

The division operation \(C = A/B\) leads to a result C plus a reminer R, where the first grossdigits are \(c_{k_K} = a_{l_L}/b_{m_M}\) and the maximal exponent is \({k_K} = {l_L}-{m_M}\).

The first partial reminder \(R^*\) is derived as: \(R^* = A - c_{k_K}{\displaystyle {{\textcircled {1}}}}^{k_K} \cdot B\). The calculation ends when either \(R^* = 0\) or the default accuracy is reached; otherwise, the number A is substituted by \(R^*\) and the computation starts again [see Sergeyev (2017)].

3.3.2 Elementary blocks module

The Elementary Blocks Module (EBM) offers common elementary functions, such as cosine, sine, exponential, and logarithm.

Each elementary function f(x) has been implemented using the truncated Taylor series:

$$\begin{aligned} f(x) = f(x_0) + \sum _{i=1}^{N} \frac{d^i f(x_0)}{dx^i} \frac{(x-x_0)^i}{i!}, \end{aligned}$$
(8)

where \(x_0\) is a finite floating-point number. For each elementary function f(x), where \(f(x) \in \{\sin (x),\) \(\cos (x),\) \(\exp (x)\), \(\log (x)\), \(x^p\) (p is finite), \(\sqrt{x}\)}, its Taylor expansion (8) is known and the analytical formulae for the respective derivatives \(\frac{d^i f(x_0)}{dx^i}\) are also known and simple to implement. For each elementary function, except \(x^p\) and \(\log (x)\), the value \(x_0\) is chosen as the finite part of the input x even if this finite part is equal to 0. For the functions \(x^p\) and \(\log (x)\), since they are not differentiable at the point \(x_0 = 0,\) then the value \(x_0\) was chosen as the finite part of x, if it is different from 0, and 0.1,  otherwise (the number 0.1 has been chosen in order to be not too small nor too large and just to keep the computations also in the case, when \(x_0 = 0\)). Since the number x and the numbers \((x-x_0)\) are grossnumbers, then the computations in this Taylor expansion are performed using the arithmetic operations implemented in the Infinity Computer library. The value N is the same as in (1), since the resulting value f(x) at a grossnumber x is also a grossnumber of the form (1).

All the blocks take as input one argument x (except the block Pow implementing the function \(x^p\), which takes also the second input p defined as the standard floating-point number), which is defined as follows:

$$\begin{aligned} x = \left[ \begin{matrix} x_0 &{} p_0\\ x_1 &{} p_1 \\ \cdots \\ x_N &{} p_N\end{matrix}\right] , \end{aligned}$$
(9)

where N is the configuration parameter with the same significance as previously. The real precision of the Infinity Computer is also defined as previously through the parameter n (i.e., the rows in (9) starting from the \((n+1)\)th contain only zeros).

In this solution, the expansions (8) have significance only if the input x is not infinite; otherwise, the Taylor series become divergent. If these elementary functions should be evaluated also at the infinite points x, then another implementations should be used (e.g., the Newton method).

Sin. This block performs the trigonometric sine of an argument x expressed as a grossnumber. The values \(\pm \sin (x_0)\) and \(\pm \cos (x_0)\) being the respective derivatives used in the Taylor formula (8) are calculated using the standard \(C++\) library math.h. Figure 4a shows a Simulink model that performs the computation \(sin(2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1})\). The result \(0.9093{\displaystyle {{\textcircled {1}}}}^{0}-0.4161{\displaystyle {{\textcircled {1}}}}^{-1}-0.4546{\displaystyle {{\textcircled {1}}}}^{-2}...\) is shown by the Display block.

Cos. This block performs the trigonometric cosine of an argument x expressed as a grossnumber. The values \(\pm \sin (x_0)\) and \(\pm \cos (x_0)\) being the respective derivatives used in the Taylor formula (8) are calculated using the standard \(C++\) library math.h. The Simulink model shown in Fig. 4b performs the computation \(cos(2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1})\). The result \(-0.4161{\displaystyle {{\textcircled {1}}}}^{0}-0.9093{\displaystyle {{\textcircled {1}}}}^{-1}-0.2081{\displaystyle {{\textcircled {1}}}}^{-2}...\) is shown by the Display block.

Exp. This block computes the base-e exponential function of a grossnumber x, which is e raised to the power \(x: e^{x}\). The value \(\exp (x_0)\) being the respective derivative used in the Taylor formula (8) is calculated using the standard \(C++\) library math.h. Figure 4c depicts a Simulink model that performs the computation \(e^{(2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1})}\). The result \(7.389{\displaystyle {{\textcircled {1}}}}^{0}+7.389{\displaystyle {{\textcircled {1}}}}^{-1}+3.695{\displaystyle {{\textcircled {1}}}}^{-2}...\) is shown by the Display block.

Log. This block allows to calculate the natural logarithm of a grossnumber x. The values \(\log (x_0)\) and \(x_0^p,\) where p is finite, used for the computation of the respective derivatives in the Taylor formula (8) are calculated using the standard \(C++\) library math.h. Figure 4d shows a Simulink model that performs the computation \(log(2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1})\). The Display block shows the result \(0.6931{\displaystyle {{\textcircled {1}}}}^{0}0.5{\displaystyle {{\textcircled {1}}}}^{-1}-0.125{\displaystyle {{\textcircled {1}}}}^{-2}+0.04167{\displaystyle {{\textcircled {1}}}}^{-3}...\) of the computation.

Pow. This block applies the function that returns the base x to the power p, defined as \(x^{p}\). The values \(x_0^q,\) where q are finite, used for the computation of the respective derivatives in the Taylor formula (8) are calculated using the standard \(C++\) library math.h. The value p is defined as a standard floating-point number. Figure 4e shows a Simulink model that performs the computation \((2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1})^{-2.5}\). The Display block shows the result \(0.1768{\displaystyle {{\textcircled {1}}}}^{0}-0.221{\displaystyle {{\textcircled {1}}}}^{-1}+0.1933{\displaystyle {{\textcircled {1}}}}^{-2}-0.415{\displaystyle {{\textcircled {1}}}}^{-3}\) of the computation.

Sqrt. This block, which has been added for convenience, uses the function defined in the Pow block to return the square root of a grossnumber \(x: \sqrt{x} = x^{1/2}\). Figure 4f shows a Simulink model that performs the computation \(\sqrt{(2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1})}\). The Display block shows the result \(1.414{\displaystyle {{\textcircled {1}}}}^{0}+0.3536{\displaystyle {{\textcircled {1}}}}^{-1}-0.04419{\displaystyle {{\textcircled {1}}}}^{-2}...\) of the computation.

Fig. 4
figure 4

Simulink models that perform the trigonometric function \(\sin {x}\) (a), the trigonometric function \(\cos {x}\) (b), the base-e exponential function \(e^{x}\) (c), the natural logarithm \(\log ~x\) (d), the base x to the exponent power p, \(x^p\), where \(p = -2.5\) e, and the square root \(\sqrt{x}\) (f) of the grossnumber \(x = 2{\displaystyle {{\textcircled {1}}}}^{0}+1{\displaystyle {{\textcircled {1}}}}^{-1}\)

Full size image

3.3.3 Utility blocks module

The Utility Blocks Module (UBM) provides common utility function blocks, which are required for supporting the implementation of models according to the Infinity Computer solution and making them compatible with the Simulink environment.

Continuous2Discrete. This utility block allows one to set the Sample Time to Discrete for all variable size blocks and Signals. It allows to sample time directly as a discrete numerical value. The produced value is used to update, during the simulation execution, the blocks internal states.

fillGrossnumber. This block adds zero rows to the matrix representation of its input in order to fix the size of all variables (by default the size of all variables representing grossnumbers is equal to 20 by 2, i.e., the number N from (2) is set to 20). Specifically, given a matrix \(M \in {\mathbb {R}}^{n \times m}\) with \(m = 2\) and \(i < n\) significant rows, the function adds an k-by-m rows of zeros, where \(k = n-i\) to fill M.

This block is required, for instance, to work with Simulink models containing algebraic loops where variable size variables are not allowed.

toGross. This block transforms a floating point number x in the corresponding matrix representation \(\left[ \begin{matrix} x&0 \end{matrix}\right] \) from (2). The so-obtained result is compatible with the Infinity Computer Simulink solution and therefore can be used as input for the other provided blocks.

getFinitePart. This block returns the finite part of a grossnumber x as a standard floating point number. For instance, given \(x = \left[ \begin{matrix} 2 &{} 1\\ 5 &{} 0\\ 3.1 &{} -5 \end{matrix}\right] \), this block returns the value 5, while for \(y = \left[ \begin{matrix} 3 &{} 2\\ 3.1 &{} -1\end{matrix}\right] \) the result is 0.

Fig. 5
figure 5

Implementations of the function \(f_1(x)\) from (10) using the proposed solution (a) and using standard Simulink blocks (b)

Full size image
Fig. 6
figure 6

The implementations of the function \(f_2(x)\) from (11) using the proposed solution (a) and using standard Simulink blocks (b)

Full size image
Fig. 7
figure 7

The implementations of the function \(f_3(x)\) from (12) using the proposed solution (a) and using standard Simulink blocks (b)

Full size image
Fig. 8
figure 8

The evaluation of the functions \(f_i(x),~i=1,2,3,\) from (10) to (12) at the points \(x_1 = 3{\displaystyle {{\textcircled {1}}}}^{0}+1.5{\displaystyle {{\textcircled {1}}}}^{-1}\) (left) and \(x_2 = 2.5{\displaystyle {{\textcircled {1}}}}^{-1.5}-3.6{\displaystyle {{\textcircled {1}}}}^{-2}+5{\displaystyle {{\textcircled {1}}}}^{-3.2}\) (right)

Full size image
Fig. 9
figure 9

Computation of the first 2 derivatives of a function f(x) at the points \(x = t\) given by the Simulink “clock” block

Full size image
Fig. 10
figure 10

Graphs of the derivatives \(f_i'(x)\) (left) and \(f_i''(x)\) (right) of the functions \(f_i(x),~i=1,2,3,\) from (10) to (12) at the interval [0, 10] obtained by the Infinity Computer and analytically. It can be seen that the graphs obtained by the Infinity Computer and by the analytical formulae coincide

Full size image

4 Assessment and evaluation

In this section, three series of numerical experiments are presented in order to evaluate the proposed solution. First, several benchmark test functions are implemented using the proposed solution and using the standard Simulink blocks. Then, these functions are evaluated using different inputs given as grossnumbers. Finally, a simple approach for the exact higher-order differentiation is implemented for these benchmarks.

4.1 Benchmark functions

In this subsection, the following three test functions from Sergeyev et al. (2016) are considered:

$$\begin{aligned} f_1(x)= & {} \frac{x^2-5x+6}{x^2+1}, \end{aligned}$$
(10)
$$\begin{aligned} f_2(x)= & {} \sin (x) + \sin (\frac{10x}{3}), \end{aligned}$$
(11)
$$\begin{aligned} f_3(x)= & {} -(16x^2 -24x + 5)e^{-x}. \end{aligned}$$
(12)

These functions have been chosen among the 24 test functions from Sergeyev et al. (2016) for the following reasons. First, they contain different elementary functions: \(f_1(x)\) is rational, \(f_2(x)\) is trigonometric, \(f_3(x)\) contains the exponential function. Second, these functions are simple to implement for a fast visualization, do not contain a lot of blocks of the same type or algebraic loops. Finally, all these functions are infinitely differentiable.

In Figs. 5, 6, and 7, the implementations of the functions \(f_i,~i=1,2,3,\) are presented using the proposed solution (a) and using standard Simulink blocks (b). One can see that these implementations are straightforward and simular. A unique difference consists of the block toGross, which transforms the input x from the traditional computational framework to the form (2) and the block getFinitePart, which returns the finite part of the result f(x). The utility blocks have been added in these implementations only to keep the computations in the traditional computational framework outside the functions, which can be useful in practice (so, there is no necessity to re-write all the implementations of the systems to the presented solution; this solution is used only where it is necessary). One can see from this figure, that the implementation of the functions in the proposed solution does not require a lot of additional knowledge about the Infinity Computer or about the low-level implementations of the Infinity Computer arithmetic. The number of the used blocks is the same, so there is no additional costs in implementation of the functions (except the addition of the utility blocks at the initial and final parts of the Simulink system, which has a constant complexity). One can see also that the results of the computation of these two implementations of the test functions at the points \(x_i^*,~i=1, 2, 3,\) from Sergeyev et al. (2016) also coincide (the points \(x_i^*\), which are the global minimizers of the functions \(f_i(x)\), respectively, have been chosen just for simplicity: the results of the computations at any finite point \(x_0\) coincide for these two implementations).

4.2 Evaluation

Let us now evaluate these functions at the inputs given as the grossnumbers, i.e., without the utility blocks toGross and getFinitePart. In Fig. 8, the results of the computation at two different points \(x_1 = 3{\displaystyle {{\textcircled {1}}}}^{0}+1.5{\displaystyle {{\textcircled {1}}}}^{-1}\) (on the left side) and \(x_2 = 2.5{\displaystyle {{\textcircled {1}}}}^{-1.5}-3.6{\displaystyle {{\textcircled {1}}}}^{-2}+5{\displaystyle {{\textcircled {1}}}}^{-3.2}\) (on the right side) are presented. The computations are kept with the precision \(n = 5\), i.e., using 5 grosspowers in (1). One can see that computations with different grossnumbers are allowed in this solution. Moreover, the grosspowers are not necessarily integer, but can be different floating-point numbers, as well. It is very important that the user could not know how the arithmetic operations are implemented inside the functions f(x). Namely, it is sufficient to give an input x and the output f(x) will be automatically generated in the form (1) without the necessity to deal with the \(C++\) class of the Infinity Computer simulator.

4.3 Exact higher-order differentiation

Let us consider now an important application of the proposed solution in the numerical analysis field. Suppose that we want to calculate the first \(k,~k\ge 1,\) derivatives of the function f(x) implemented using the Simulink arithmetic blocks. Traditionally [see Karris (2006b)], the internal Simulink block “Derivative” allows one to calculate the derivatives only using the finite forward differences, which are usually not accurate. Moreover, since using the forward differences for computation of the first \(k,~k\ge 1,\) derivatives, at least \(k+1\) observations of the function f(x) are needed, then the values of the derivatives at the first \(x_0,\) \(x_1,\) ...\(,x_{k-1}\) points cannot be calculated using the Simulink’s “derivative” blocks. The obtained error is of order 1, i.e., proportional to the Simulink’s system sample time \(\Delta t\), and often cannot be small enough due numerical cancellation errors.

Another possibility to calculate the exact higher-order derivatives in Simulink is using external packages, e.g., for automatic differentiation. However, this solution has several disadvantages. First, using external packages requires additional knowledge on how they work and how to use them. Second, if the function f(x) is difficult and uses a lot of subsystems and external dependencies, then the resulting formulae or systems obtained by the automatic differentiation can be too difficult and can require a lot of computational resources to generate them. Moreover, in this case, the evaluation of the higher-order derivatives can be too slow or even impossible [see, e.g., Iavernaro et al. (2020a)].

Let us see, how the higher-order derivatives can be calculated on the Infinity Computer. Suppose that the function f(x) has only finite values at the finite points x (i.e., it does not depend on \({\displaystyle {{\textcircled {1}}}}\)). Suppose also that there exists the (unknown) Taylor expansion of the function f(x) around the finite point \(x_0\). Then, the result of the computation of f(x) at the point \(x_0 + {\displaystyle {{\textcircled {1}}}}^{-1}\) truncated after \(k+1\) grosspowers gives us the exactFootnote 2 higher-order derivatives of the function f(x) at the point \(x_0\):

$$\begin{aligned} f(x_0 + {\displaystyle {{\textcircled {1}}}}^{-1}) = f_0 + f_1\cdot {\displaystyle {{\textcircled {1}}}}^{-1} + ... + f_k \cdot {\displaystyle {{\textcircled {1}}}}^{-k}, \end{aligned}$$
(13)

from where one can obtain that \(f(x_0) = f_0,\) \(f'(x_0) = f_1,\) \(f''(x_0) = f_2 \cdot 2!,\)..., \(f^{(k)}(x) = f_k \cdot k!\) [see Sergeyev (2011a, (2017) for details].

In Fig. 9, the Simulink subsystem for computation of the first 2 derivatives of a function f(x) implemented in the subsystem “f(x)” at the time steps t using the proposed solution of the Infinity Computer is presented. Since the derivative is calculated with respect to the time t, then let us call the functions f(x) as the functions depending on time t, i.e., f(t), hereinafter. First, the input t given by the standard Simulink block “clock” is transformed to the grossnumber \(t_{gross}\) by the block “toGross”. Then, the infinitesimal \({\displaystyle {{\textcircled {1}}}}^{-1}\) expressed by the constant block is added to the transformed input \(t_{gross}\). The obtained grossnumber is moved to the input of the block “f(x)”. The output of the block “f(x)” is multiplied by \({\displaystyle {{\textcircled {1}}}}\) and the result arrives to the block “getFinitePart” (from where the value \(f'(t)\) is obtained), at the same time the output of the block “f(x)” is multiplied by \(2{\displaystyle {{\textcircled {1}}}}^{2}\) and the result arrives to the block “getFinitePart” as well (from where the value \(f''(t)\) is obtained). The obtained values of the derivatives arrive to the scope blocks in order to construct their graphs.

The graphs of the first two derivatives for each test function \(f_i(t),~i=1,2,3,\) from (10) to (12) are presented in Fig. 10, from where one can see that the derivatives obtained by the Infinity Computer coincide with the exact derivatives obtained analytically.

One can see that the differentiation using the presented solution is simple and almost does not require any additional knowledge and/or tools. Higher-order derivatives can be easily calculated using only the proposed blocks without the necessity of an additional specific tool or block. More applications are provided in the accompanying paper [see Falcone et al. (2020a)].

5 Conclusion

A new Simulink-based software solution to the Infinity Computer has been proposed in this paper. This solution uses the software simulator of the Infinity Computer written in \(C++\) according to the patents [see Sergeyev (2010a)] and loaded in Matlab using MEX-files for the implementation of the low-level arithmetic. The proposed solution is user-friendly, simple, general purpose and domain independent, i.e., it can be used in any domain where a high precision of the computations is required.

Four arithmetic blocks representing four operations \(+\), −, \(\times \), and /, have been proposed as well as the blocks for the elementary functions \(\sin (x)\), \(\cos (x)\), \(\exp (x)\), \(\log (x)\), \(x^p\), and \(\sqrt{x}\). Moreover, four utility blocks for supporting the implementation of models have been also proposed. The usage of the proposed blocks is similar to their internal Simulink analogues, so it does not require any additional tools or sophisticated techniques.

The solution has been evaluated on three benchmark test problems. It has been shown that the complexity of implementation of the functions using the proposed solution and using traditional Simulink blocks is the same, while the proposed solution allows one to use all the potentiality of the Infinity Computer in Simulink without the necessity of referring to the low-level implementation of the procedures on the Infinity Computer. As an example of the potential usage of the solution, an exact higher-order differentiation of the univariate functions has been considered. It has been shown that the proposed solution allows one to calculate the exact higher-order derivatives in a simple and efficient way without using any additional tool.

Future research efforts will be devoted to: (1) improve and extend the proposed solution to support a wider set of concepts and operations delineated by the Infinity Computer; (2) perform further experimentations of the solution in different application domains.