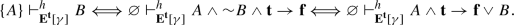Don’t you therefore see that in this way from this impossibility, that Socrates is a man and Socrates is not a man, anything follows?
Alexander Neckam.
Abstract
This paper gives an account of Anderson and Belnap’s selection criteria for an adequate theory of entailment. The criteria are grouped into three categories: criteria pertaining to modality, those pertaining to relevance, and those related to expressive strength. The leitmotif of both this paper and its prequel is the relevant legitimacy of disjunctive syllogism. Relevant logics are commonly held to be paraconsistent logics. It is shown in this paper, however, that both E and R can be extended to explosive logics which satisfy all of Anderson and Belnap’s selection criteria, provided the truth-constant known as the Ackermann constant is available. One of the selection criteria related to expressive strength is having an “enthymematic” conditional for which a deduction theorem holds. I argue that this allows for a new interpretation of Anderson and Belnap’s take on logical consequence, namely as committing them to pluralism about logical consequence.
Similar content being viewed by others
1 Introduction
Tradition has it that relevant logics are inherently paraconsistent; that is they don’t license the inference from the premise set  to B for arbitrary A’s and B’s. In the prequel to this paper, Non-Boolean Classical Relevant Logics I, I presented a logic \({\Pi '}_{\!\!\mathbf{E} }\) which has both the variable sharing property, the Entailment theorem, the enthymematical deduction theorem, as well as a definable S4 modality. The Hilbert consequence relation of \({\Pi '}_{\!\!\mathbf{E} }\), however, is not paraconsistent, but explosive and therefore validates the principles called disjunctive syllogism; the rule
to B for arbitrary A’s and B’s. In the prequel to this paper, Non-Boolean Classical Relevant Logics I, I presented a logic \({\Pi '}_{\!\!\mathbf{E} }\) which has both the variable sharing property, the Entailment theorem, the enthymematical deduction theorem, as well as a definable S4 modality. The Hilbert consequence relation of \({\Pi '}_{\!\!\mathbf{E} }\), however, is not paraconsistent, but explosive and therefore validates the principles called disjunctive syllogism; the rule  is derivable for arbitrary A’s and B’s. \({\Pi '}_{\!\!\mathbf{E} }\) is quite closely related to Anderson and Belnap’s favorite logic E. In order to prove the variable sharing property, however, the transitivity axioms of E had to be weakened ever so slightly. As a result, its modal features had to be added as primitive postulates. Ever since Ackermann (1956) (who did so under inspiration from Johansson) have logicians considered adding truth-constants to relevant logics in order to increase expressivity. This paper shows that one can do better than \({\Pi '}_{\!\!\mathbf{E} }\) provided that ‘\(\mathbf{t} ,\)’ the truth-constant known as the Ackermann constant, is admitted into the language.
is derivable for arbitrary A’s and B’s. \({\Pi '}_{\!\!\mathbf{E} }\) is quite closely related to Anderson and Belnap’s favorite logic E. In order to prove the variable sharing property, however, the transitivity axioms of E had to be weakened ever so slightly. As a result, its modal features had to be added as primitive postulates. Ever since Ackermann (1956) (who did so under inspiration from Johansson) have logicians considered adding truth-constants to relevant logics in order to increase expressivity. This paper shows that one can do better than \({\Pi '}_{\!\!\mathbf{E} }\) provided that ‘\(\mathbf{t} ,\)’ the truth-constant known as the Ackermann constant, is admitted into the language.
Relevant logics came about as an attempt at providing a theory of entailment, that is, logical consequence, free of the so-called paradoxes of implication. Not only, however, did they seek a new concept of entailment, Anderson and Belnap argued in their Grammatical propaedeutic—the appendix to Anderson and Belnap (1975)—that even though entailment belongs to the “meta-language,” this is merely a grammatical fact with little or no significance for theorizing about logical consequence. They therefore sought not only a new concept of entailment, but a theory of entailment in which entailment itself was to be expressible.Footnote 1 In Ackermann’s first attempt at such a conditional it is clear that the conditional is added to classical logic: the \(\rightarrow \)-free fragment of Ackermann’s logic \({\Pi '}\) is classical logic. Thus one might simply view \({\Pi '}\) as harboring two notions of conditionality: that expressed by the material conditional and that expressed by what Ackermann called strenge Implikation—the added connective \(\rightarrow \). This sets Ackermann’s approach apart from that of Anderson and Belnap (A&B from now on).
As we shall see, A&B also sought a theory of entailment with two kinds of conditionals. Their favorite logic E—their “logic of entailment”—is obtained by essentially dropping from \({\Pi '}\) its primitive rule  —that is modus ponens for the material conditional, or disjunctive syllogism, named by Ackermann as simply \((\gamma )\). Not only did A&B regard the material conditional as not expressing entailment—in fact they acknowledged that “it is not unmistakably clear whether or not anyone ever seriously took material implication to express ‘valid argument’ ” (Anderson and Belnap 1961, p. 715)—but thought furthermore that the material conditional should not even be viewed as a conditional: “But of course \({\overline{A}} \vee B\) is no kind of conditional, since modus ponens fails for it, as we have remarked ad nauseam before.” (Anderson and Belnap 1975, p. 259).Footnote 2 Of course, if all they intended by claiming that modus ponens fails for the material conditional is that it fails in the case of E, that would be rather uninteresting. What I take them to argue, however, is that the properties of any theory of entailment are such as to rule out modus ponens holding for the material conditional; in short, they claim that modus ponens for the material conditional fails on broadly conceived relevant grounds. The main purpose of this paper is to show that this is not the case, not even if, to borrow A&B’s phrase,Footnote 3 we bend over backward trying to be fair to their “non-official” position and require that the theory contains all that A&B’s theory contains, i.e. that the logic extends E, without, of course, extending it too much so as to loose the properties deemed valuable by A&B.
—that is modus ponens for the material conditional, or disjunctive syllogism, named by Ackermann as simply \((\gamma )\). Not only did A&B regard the material conditional as not expressing entailment—in fact they acknowledged that “it is not unmistakably clear whether or not anyone ever seriously took material implication to express ‘valid argument’ ” (Anderson and Belnap 1961, p. 715)—but thought furthermore that the material conditional should not even be viewed as a conditional: “But of course \({\overline{A}} \vee B\) is no kind of conditional, since modus ponens fails for it, as we have remarked ad nauseam before.” (Anderson and Belnap 1975, p. 259).Footnote 2 Of course, if all they intended by claiming that modus ponens fails for the material conditional is that it fails in the case of E, that would be rather uninteresting. What I take them to argue, however, is that the properties of any theory of entailment are such as to rule out modus ponens holding for the material conditional; in short, they claim that modus ponens for the material conditional fails on broadly conceived relevant grounds. The main purpose of this paper is to show that this is not the case, not even if, to borrow A&B’s phrase,Footnote 3 we bend over backward trying to be fair to their “non-official” position and require that the theory contains all that A&B’s theory contains, i.e. that the logic extends E, without, of course, extending it too much so as to loose the properties deemed valuable by A&B.
A&B never gave a systematic presentation of their selection criteria for a theory of entailment, and so just what properties they did deem valuable is open for interpretation. In this paper I have tried to give a more systematic account of what I take to be A&B’s selection criteria and some of the reasons at least for why they opted for these. I have categorized the criteria into three main categories:
-
modality;
-
relevance properties; and
-
expressive strength.
A&B thought of entailment as a modal notion and thought that modality ought to be expressible within the theory of entailment. The theory of entailment should, according to A&B, be strong enough to express modality, but not too strong so as to trivialize the modality, or so as to validate so-called modal fallacies. I call a theory of entailment which satisfies these criteria modally nice. Section 2 will first define what I call the Hilbertian consequence relation for any logic. It also shows how A&B’s favorite logics E and R are pieced together. Section 3 then introduces the truth-constants known as the Ackermann constant \(\mathbf{t} \) and the Church constant \(\top \) and defines the explosive logics Æ and M. The logics Æ and M are new with this paper. Relevant logics are known for not validating the explosion axiom  unrestrictedly. Note, then, that Æ and M are obtained from, respectively, \(\mathbf{E} ^\mathbf{t \top }\)—E augmented by the Ackermann and Church constants—and \(\mathbf{R} ^\mathbf{t \top }\) by adding the axiom \(\mathbf{t} \wedge \mathbf{f} \rightarrow A\), where
unrestrictedly. Note, then, that Æ and M are obtained from, respectively, \(\mathbf{E} ^\mathbf{t \top }\)—E augmented by the Ackermann and Church constants—and \(\mathbf{R} ^\mathbf{t \top }\) by adding the axiom \(\mathbf{t} \wedge \mathbf{f} \rightarrow A\), where  . Section 4 then looks at the modal features of \(\mathbf{E} ^\mathbf{t} \) and Æ and shows how to extend them into S5-type modal logics. Here I will properly state what I take the property of modal niceness to be and will show that both \(\mathbf{E} ^\mathbf{t} \) and Æ are in fact modally nice. Section 5 then digresses on the topic of conservative extension. It turns out that Æ and Æ5 do not conservatively extend E, but rather interpret, respectively, classical modal S4 and S5. M, on the other hand, conservatively extends R. That this is so follows from the fact that these logics are closely related to CE and CR, E and R with Boolean negation added.Footnote 4
. Section 4 then looks at the modal features of \(\mathbf{E} ^\mathbf{t} \) and Æ and shows how to extend them into S5-type modal logics. Here I will properly state what I take the property of modal niceness to be and will show that both \(\mathbf{E} ^\mathbf{t} \) and Æ are in fact modally nice. Section 5 then digresses on the topic of conservative extension. It turns out that Æ and Æ5 do not conservatively extend E, but rather interpret, respectively, classical modal S4 and S5. M, on the other hand, conservatively extends R. That this is so follows from the fact that these logics are closely related to CE and CR, E and R with Boolean negation added.Footnote 4
An adequate theory of entailment must, according to A&B, avoid the “implicational paradoxes.” Such paradoxes are branded fallacies of relevance by A&B as they, intuitively, are claims of logical entailment where the premises are irrelevant to the conclusion. A&B presented two formal criteria to safe-guard against such paradoxes: the variable sharing property and the Entailment theorem. The first such criterion is usually stated for logics without truth-constants. Section 6 discusses the variable sharing property in the context of truth-constants. It is shown that Æ and M satisfy the same variable sharing properties as \(\mathbf{E} ^\mathbf{t \top }\) and \(\mathbf{R} ^\mathbf{t \top }\) do. In fact it is shown that the two available suggestions for how to deal with such constants are equivalent. The Entailment criterion is often called the use-criterion as it it was thought to ensure that if A entails B, then every proof of B must somehow use A. A&B viewed this criterion as necessary and sufficient for avoiding the relevant fallacies. However, it was shown in the prequel to this paper that even though E and R do satisfy the use-criterion, so does classical logic. The proof applies to any sufficiently strong logic in the vicinity of E having no more rules than adjunction and modus ponens. Section 8 shows how to slightly alter the notion of a relevant deduction so as to make the Entailment theorem provable also for logics with disjunctive syllogism as a primitive rule.
Not only should a theory of entailment be such as to avoid the modal and relevant fallacies, but it should have certain properties best viewed as relating to expressive strength. I should note already now, however, that this is where I find A&B to be the most unclear. I’ve marked out two such “effable” properties, namely having a definable “enthymematic” conditional for which a deduction theorem relative to the Hilbert consequence relation holds, and having the property of rule normality. These are both dealt with in Sect. 7. I both state A&B’s reasons for wanting an enthymematic conditional and show that Æ and M are alike \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \) in validating the deduction theorem with regards to the conditional \(A \mapsto B =_{df} A \wedge \mathbf{t} \rightarrow B\). It is also shown that even though \(\mapsto \) does not have this feature in \(\mathbf{E} ^\mathbf{t} [\gamma ]\)—\(\mathbf{E} ^\mathbf{t} \) augmented by \((\gamma )\)—and \(\mathbf{R} ^\mathbf{t} [\gamma ]\), a different enthymematic conditional, namely \(A \hookrightarrow B =_{df} A \wedge \mathbf{t} \rightarrow \mathbf{f} \vee B\), does. A&B stated that adding \((\gamma )\) to E “destroys practically every nice property of E” (Anderson et al. 1992, p. 138). One such property which is left rather implicit by A&B is that of rule normality, that any primitive rule of the theory of entailment should by the lights of the theory itself be a true entailment. From the definition of rule normality it will be evident that \(\mathbf{E} ^\mathbf{t} , \mathbf{R} ^\mathbf{t} \), Æ, and M are all rule-normal logics, but that \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\) are not.
A&B’s selection criteria for an adequate theory of entailment, then, do not differentiate between \(\mathbf{E} ^\mathbf{t} (\mathbf{R} ^\mathbf{t} )\) and Æ(M), and so the conclusion is that the material conditional does not fail to be a proper conditional on, broadly conceived, relevant grounds. Even though the main goal is in this sense negative, this paper contributes positively to the philosophy of relevant logics and should therefore also be of interest to those who think, for whatever reason, that modus ponens in fact fails to hold for the material conditional. In addition to, to highlight some of what I’ve already stated, (i) systematizing the adequacy criteria of Anderson and Belnap, (ii) showing that logics with \((\gamma )\) as a primitive rule can satisfy the Entailment theorem and (iii) have an enthymematical deduction theorem, this paper also provides a new interpretation of A&B’s often highly polemical and often unsystematic philosophy of logic. Relevant logics are philosophically often presented as monistic theories of logical consequence: in some cases it is the Hilbertian consequence relation which is thought of as logical consequence, whereas in other cases it is a different “relevant” notion of logical consequence which is presented as the one true theory of logical consequence. As we shall see, A&B are quite explicit on their misgivings about the Hilbertian consequence relation, and so it would stand to reason that they regarded their notion of relevant consequence as the one true theory of logical consequence. Section 9 displays how the Hilbertian and A&B’s version of a relevant consequence relation of \(\mathbf{E} ^\mathbf{t} , \mathbf{E} ^\mathbf{t} [\gamma ]\) and Æ are related before Sect. 10suggests a philosophically unifying theory under which to make, I think, a more fruitful account of A&B’s view of logical consequence, namely as adhering to pluralism about logical consequence, and more precisely to the type of pluralism Hjortland (2013) calls intra-theoretic pluralism. Section 11 then finally summarizes.
Although this paper is a sequel to Øgaard (2019), I’ve tried to make it as independent as possible so as to make them independently readable. As a result, they do occasionally overlap.
2 E, R and the Hilbert consequence relation
This section defines the Hilbert consequence relation of a logic and presents the axioms and rules of the logics E and R. The following section then introduces the Ackermann and Church constants and defines the explosive siblings of E and R, namely Æ and M.
Every logic in this paper will be thought of as a set of axioms together with a set of rules. Rules will be on the form \(\varGamma \Vdash A\) where \(\varGamma \) is a finite set. For each logic there are two different consequence relations which both will be important in this paper. The easiest one to specify is the Hilbert consequence relation for a logic:
Definition 1
(The Hilbert consequence relation) A Hilbert proof of a formula A from a set of formulas \(\varGamma \) in the logic L is defined to be a finite list \(A_1, \ldots , A_n\) such that \(A_n = A\) and every \(A_{i\le n}\) is either a member of \(\varGamma \), a logical axiom of L, or there is a set \(\varDelta \subseteq \{A_j \mathbin {|} j<i\}\) such that \(\varDelta \Vdash A_i\) is an instance of a rule of L. The existential claim that there is such a proof is written \(\varGamma \vdash ^{h}_\mathbf{L } A\) and expressed as “there exists a Hilbert-derivation of A from \(\varGamma \) in the logic L,” or more casually as “the rule \(\varGamma \vdash ^{h} A\) is derivable in L.”
The notion of a derivable rule does apply to consequence relations in general. It is, however, important to distinguish between such derivable rules from merely admissible rules. The following definition makes this distinction clear:
Definition 2
(Admissible vs. derivable rules) A rule \(\{A_1, \ldots , A_n\} \Vdash B\) is derivable for a logic L and consequence relation \(\vdash \) just in case \(\{A_1, \ldots , A_n\} \vdash B\) holds. The rule is said to be admissible if \(\varnothing \vdash B\) whenever \(\varnothing \vdash A_i\) for all \(i \le n\).
Definition 3
(Explosive versus paraconsistent consequence relations) A consequence relation \(\vdash \) is explosive just in case  holds for every A and B, and paraconsistent if not.
holds for every A and B, and paraconsistent if not.
Note, then, that a consequence relation may be paraconsistent, yet have the explosion rule  as an admissible rule. The Hilbert consequence relation \(\vdash ^h\) for relevant logics such as E and R is paraconsistent. However, Meyer and Dunn showed in Meyer and Dunn (1969) that the rule
as an admissible rule. The Hilbert consequence relation \(\vdash ^h\) for relevant logics such as E and R is paraconsistent. However, Meyer and Dunn showed in Meyer and Dunn (1969) that the rule  is admissible for both \(\vdash ^h_\mathbf{E }\) and \(\vdash ^h_\mathbf{R }\). From this it easily follows that the explosion rule is admissible for both logics.
is admissible for both \(\vdash ^h_\mathbf{E }\) and \(\vdash ^h_\mathbf{R }\). From this it easily follows that the explosion rule is admissible for both logics.
Definition 4
(Parenthesis conventions and defined connectives) \(\vee \) and \(\wedge \) are to bind tighter than \(\rightarrow \), and so I’ll usually drop parenthesis enclosing conjunctions and disjunctions whenever possible. The material conditional \(\supset \), relevant equivalence \(\leftrightarrow \), the modal operators \(\Box \) and \(\Diamond \), the strict conditional  , and the two enthymematic conditionals \(\mapsto \) and \(\hookrightarrow \) are defined as follows:
, and the two enthymematic conditionals \(\mapsto \) and \(\hookrightarrow \) are defined as follows:

Definition 5
(E) The following list of axioms and rules defines the logic E:

Lemma 1
Any logic considered in this paper will have the following derived rules:

Proof
Left for the reader. \(\square \)
As we shall see in the next section, E is a S4 type modal logic. The stronger logic R, on the other hand, was from the outset thought of as a non-modal logic.
Definition 6
(R) R is obtained by adding (Ax15), the axiom called assertion, to E and deleting the then superfluous (Ax13) and (Ax14).

It is easy to see that the modal reading of \(\Box A\) is lost in R since \(A \rightarrow \Box A\) is in fact an instance of the assertion axiom. This is why A&B differentiate between entailment, which they take to be a modal concept, and the non-modal concept of implication in that they talk of E as a (the) logic of entailment, whereas the R is “merely” a logic of relevant implication.
3 Introducing truth-constants and the explosive logics Æ and M
A&B’s E was obtained as a modification of Ackermann’s logic \({\Pi '}\) from Ackermann (1956). Ackermann augmented his logic \({\Pi '}\) with a truth-constant, \(\curlywedge \), which was to be read das Absurde, and defined \(\Box A\) as  . A&B then realized that \(\Box A\) can in fact be equivalently defined as \((A \rightarrow A) \rightarrow A\), and showed in Anderson and Belnap (1959) that \(\Box \) defined this way has the modal features of a S4 modality. \({\Pi '}\) and E turn out to be theorem-vise identical, and so E has this feature as well. Thus \(\curlywedge \) is not needed in E for the S4 modality to obtain, and so E was originally formulated without truth-constants. In Anderson and Belnap (1975, § 27.1.2), however, they do consider adding a positive variant of \(\curlywedge \), namely \(\mathbf{t} \), to both E and R. The nice feature of doing so is that \(\Box A \leftrightarrow (\mathbf{t} \rightarrow A)\) becomes a theorem, and so being necessarily true and being entailed by \(\mathbf{t} \) turn out to be equivalent. This is a significant expressive enhancement as E without \(\mathbf{t} \) has no uniform way of expressing the claim that A is entailed by logic.
. A&B then realized that \(\Box A\) can in fact be equivalently defined as \((A \rightarrow A) \rightarrow A\), and showed in Anderson and Belnap (1959) that \(\Box \) defined this way has the modal features of a S4 modality. \({\Pi '}\) and E turn out to be theorem-vise identical, and so E has this feature as well. Thus \(\curlywedge \) is not needed in E for the S4 modality to obtain, and so E was originally formulated without truth-constants. In Anderson and Belnap (1975, § 27.1.2), however, they do consider adding a positive variant of \(\curlywedge \), namely \(\mathbf{t} \), to both E and R. The nice feature of doing so is that \(\Box A \leftrightarrow (\mathbf{t} \rightarrow A)\) becomes a theorem, and so being necessarily true and being entailed by \(\mathbf{t} \) turn out to be equivalent. This is a significant expressive enhancement as E without \(\mathbf{t} \) has no uniform way of expressing the claim that A is entailed by logic.
Definition 7
(Connective extension) If L is a logic, then \(\mathbf{L} ^\top \) and \(\mathbf{L} ^\mathbf{t }\) are the logics obtained by adding to L, respectively, the following sets of axioms and definitions:

In Øgaard (2019) the axiom  was added to a logic slightly weaker than E. The resultant logic—\({\Pi '}_{\!\!\mathbf{E} }\)—satisfies the variable sharing property and so
was added to a logic slightly weaker than E. The resultant logic—\({\Pi '}_{\!\!\mathbf{E} }\)—satisfies the variable sharing property and so  is not a theorem of it. It was shown, however, that that axiom needs further weakening if one is to add it to \(\mathbf{R} ^\top \) without yielding
is not a theorem of it. It was shown, however, that that axiom needs further weakening if one is to add it to \(\mathbf{R} ^\top \) without yielding  and
and  . A&B noted in fact that if C is any conjunction of axioms of R, then
. A&B noted in fact that if C is any conjunction of axioms of R, then  fails in Belnap’s test model of relevance (Anderson and Belnap 1975, p. 298). They did not, however, show that the same holds for \(\mathbf{R} ^\mathbf{t} \); in fact, as first noted in Øgaard (2017, p. 211),
fails in Belnap’s test model of relevance (Anderson and Belnap 1975, p. 298). They did not, however, show that the same holds for \(\mathbf{R} ^\mathbf{t} \); in fact, as first noted in Øgaard (2017, p. 211),  , and therefore (using distribution)
, and therefore (using distribution)  is in fact validated in Belnap’s test model. These two formulas are in fact equivalent to (Ax18) below, which are used in defining the logics Æ and M:
is in fact validated in Belnap’s test model. These two formulas are in fact equivalent to (Ax18) below, which are used in defining the logics Æ and M:
Definition 8
(Æ and M) Æ and M are hereby defined as, respectively, \(\mathbf{E} ^\mathbf{t \top }\)Footnote 5 and \(\mathbf{R} ^\mathbf{t \top }\) strengthened by
Æ is so named since the letter naming it is formed from the letter ‘A’ for ‘Ackermann’ and ‘E’ for ‘entailment.’ M is so named in honor of Robert Meyer who, as I will get back to later, argued for strengthening R with Boolean negation which turns out to be a slightly stronger logic than M. Æ & M are my proposals for how one could extend E & R while keeping, as we shall see,
-
in the case of Æ, the modal niceness of E
-
the relevance properties, i.e. the Entailment theorem and the variable sharing property
-
the two properties pertaining to expressiveness, namely the enthymematical deduction theorem and the property of rule normality
all this while at the same time having modus ponens for the material conditional, the rule

as a derivable rule for the consequence relation \(\vdash ^h\). Note, then, that Æ and M are explosive logics with regards to the Hilbert consequence relation: the rule  is derivable for both logics for arbitrary A’s and B’s. Even though \((\gamma )\) is admissible for both \(\vdash ^h_\mathbf{E }\) and \(\vdash ^h_\mathbf{R }\) (cf. Meyer and Dunn 1969), both E and R have a paraconsistent \(\vdash ^h\)-relation. Æ and M, however, both extend classical logic in that every valid rule of classical logic applies unrestrictedly to \(\vdash ^h\) for both Æ and M.Footnote 6 In other words, then, Æ & M preserve everything good about E & R, while validating not only the logical truths of classical logic as E & R do, but also every classically valid rule.
is derivable for both logics for arbitrary A’s and B’s. Even though \((\gamma )\) is admissible for both \(\vdash ^h_\mathbf{E }\) and \(\vdash ^h_\mathbf{R }\) (cf. Meyer and Dunn 1969), both E and R have a paraconsistent \(\vdash ^h\)-relation. Æ and M, however, both extend classical logic in that every valid rule of classical logic applies unrestrictedly to \(\vdash ^h\) for both Æ and M.Footnote 6 In other words, then, Æ & M preserve everything good about E & R, while validating not only the logical truths of classical logic as E & R do, but also every classically valid rule.
The truth-constants are all undefinable in all of E, and R. \(\top \) is to be thought of as the disjunction of every formula and is interpreted as the top element in every algebra. In \(\mathbf{E} ^\mathbf{t} \) and Æ, \(\mathbf{t} \) should be be thought of as the conjunction of every logical truth, whereas in R and M simply as the conjunction of every truth. The reason why R and M’s interpretation of \(\mathbf{t} \) is legitimate is simply that the rule \(\{{A}\} \vdash ^h \mathbf{t} \rightarrow A\) is derivable for these logics. Thus for R and M one may for any sentence A infer that A is entailed by \(\mathbf{t} \) from the assumption that A is simply true. Thus “conjunction of every truth” should, given that \(\varGamma \) is the set of premises, be read as meaning \(\bigwedge \{A \mathbin {|} \varGamma \vdash ^h A\}\)—the conjunction of the theory generated from \(\varGamma \) using the Hilbert consequence relation.Footnote 7 In fact, \(A \leftrightarrow (\mathbf{t} \rightarrow A)\) is a theorem of both \(\mathbf{R} ^\mathbf{t} \) and M, and so A is equivalent to being implied by \(\mathbf{t} \) in these logics. In contrast, \(\mathbf{t} \) in \(\mathbf{E} ^\mathbf{t} \) and Æ should rather be interpreted as \(\bigwedge \{A \mathbin {|} \varnothing \vdash ^h A\}\) since the rule \(\{A\} \vdash ^h \mathbf{t} \rightarrow A\) is not derivable in either \(\mathbf{E} ^\mathbf{t} \) or Æ, but is merely admissible.Footnote 8 That this is so follows from Øgaard (2019, thm. 1) which states that the rule \(\{A\} \vdash ^h \Box A\) is admissible in any \(\rightarrow \)-axiomatic extension of E, together with the fact the rule is not derivable in either of \(\mathbf{E} ^\mathbf{t} \) or Æ as the model in Fig. 1 shows,Footnote 9 together with, finally, the following lemma:
Lemma 2
\(\varnothing \vdash ^h_\mathbf{L } \Box A \leftrightarrow (\mathbf{t} \rightarrow A)\) where L is any extension of \(\mathbf{E} ^\mathbf{t} \).
Proof
See Routley et al. (1982, p. 409) or Mares and Standefer(2017, p. 702). \(\square \)
That \(\mathbf{E} ^\mathbf{t} \) and Æ make the necessitation rule admissible, but not derivable, and that this is so also for the rule \(\{A\} \vdash ^h \mathbf{t} \rightarrow A\), tells in favor of interpreting \(\Box \) as logical necessity and \(\mathbf{t} \) as the conjunction of every logical truth. It is only fitting, then, that being necessarily true should coincide with being entailed by logic itself as Lemma 2 shows.Footnote 10 The next section further expands upon the modal features of \(\mathbf{E} ^\mathbf{t} \) and Æ.
4 Modal properties of E t and Æ
A&B thought of the conditional of E as itself expressing entailment. Entailment, according to A&B, is a modal concept, and so their theory of entailment was shown to harbor a definable S4 modal operator. In order for the definable \(\Box \) to legitimately be a modal operator expressing necessity according to the theory of entailment itself, however, or so I take A&B’s view to be, it should be the case that the S4-characteristic axioms should themselves be provable entailment statements (cf. Anderson and Belnap 1975, §§ 5.2 & 11). Furthermore, for \(\Box \) to express necessity, the rule \(\{A \}\vdash ^h \Box A\) should not be derivable, although it should be admissible (cf. Anderson and Belnap 1975, § 21.2.2).
In addition to there being fallacies of relevance, A&B thought that there were modal fallacies. They regarded a proposition as being necessitive if it was equivalent to a necessary one, that is A is necessitive if and only if it is equivalent to \(\Box B\) for some B. Roughly, their view was that only necessitives could stand in the entailment relation to other necessitives; any entailment statement to the contrary amounts to, according to A&B, a modal fallacy.Footnote 11 A&B viewed entailment statements as necessitives, but propositions expressed using only negation, conjunction and disjunction as non-necessitives. In the formal theory of entailment, then, it should not be the case that any formula A over the  -fragment of the language should entail any formula \(B \rightarrow C\). This is known as the Ackermann property.
-fragment of the language should entail any formula \(B \rightarrow C\). This is known as the Ackermann property.
Let’s collect A&B’s criteria for theory choice pertaining to modality into a definition:
Definition 9
(Modally nice) A logic with an entailment-operator \(\rightarrow \) is modally nice just in case it
-
satisfies the Ackermann property relative to \(\rightarrow \),
-
has a definable modal operator with the S4-characteristics expressible as \(\rightarrow \)-entailments, and
-
is such as to yield the necessity rule as an admissible, but not derivable rule.
This section shows that E and Æ are alike in that both are modally nice. It is also shown how to extend E and Æ so as to make them into S5-type modal logics.
Theorem 1
The following are all valid in \(\mathbf{E} ^\mathbf{t} \) and Æ:

Proof
- \((\mathbf{K} )\) :
-
$$\begin{aligned} \begin{array}{lll} (1) &{} (A \rightarrow B) \rightarrow ((\mathbf{t} \rightarrow A) \rightarrow (\mathbf{t} \rightarrow B))&{} {Ax8}\\ (2) &{}(\mathbf{t} \rightarrow (A \rightarrow B)) \rightarrow (A \rightarrow B) &{} \mathbf{t 2}\\ (3) &{} (\mathbf{t} \rightarrow (A \rightarrow B)) \rightarrow ((\mathbf{t} \rightarrow A) \rightarrow (\mathbf{t} \rightarrow B))&{} \text{1, } \text{2, } \text{ transitivity }\\ (4) &{} (\mathbf{t} \rightarrow B) \rightarrow \Box B&{} {Lemma 2}\\ (5) &{} (\mathbf{t} \rightarrow (A \rightarrow B)) \rightarrow ((\mathbf{t} \rightarrow A) \rightarrow \Box B)&{} {3, 4}, rightER\\ (6) &{} \Box A \rightarrow (\mathbf{t} \rightarrow A) &{} {Lemma 2}\\ (7) &{} (\mathbf{t} \rightarrow (A \rightarrow B)) \rightarrow (\Box A \rightarrow \Box B)&{} {5, 6}, leftER\\ (8) &{} \Box (A \rightarrow B) \rightarrow (\mathbf{t} \rightarrow (A \rightarrow B)) &{} {Lemma 2}\\ (9) &{} \Box (A \rightarrow B) \rightarrow (\Box A \rightarrow \Box B)&{} {7, 8}, transitivity, \text{ def. } \text{ of } \Box \\ \end{array} \end{aligned}$$
- \((\mathbf{T} )\) :
-
Instance of (Ax13).
- \((\Box \wedge )\) :
-
This is simply (Ax14).
- \((\mathbf{4} )\) :
-
$$ \begin{aligned} \begin{array}{lll} (1) &{} (\mathbf{t} \rightarrow A) \rightarrow ((\mathbf{t} \rightarrow \mathbf{t} ) \rightarrow (\mathbf{t} \rightarrow A))&{} {Ax8}\\ (2) &{}\mathbf{t} \rightarrow (\mathbf{t} \rightarrow \mathbf{t} )&{} \mathbf{t 1}\\ (3) &{} (\mathbf{t} \rightarrow A) \rightarrow (\mathbf{t} \rightarrow (\mathbf{t} \rightarrow A))&{} {1, 2}, leftER\\ (4) &{} \Box A \rightarrow \Box \Box A&{} {3}, Lemma 2 \& \text{ fiddling } \end{array} \end{aligned}$$
- \((\mathbf{N} )\) :
-
See Øgaard (2019, thm. 1).
-
 :
: -
Counter-model in Fig. 1.
\(\square \)
In the same manner as for the ordinary modal logic S4, one can now show that E and Æ only have 14 non-equivalent modalities, namely for any formula A,

Lemma 2 above showed that \(\Box A\) and \(\mathbf{t} \rightarrow A\) are equivalent. We now see that the notion of necessity at work in both \(\mathbf{E} ^\mathbf{t} \) and Æ is that of a S4 modality. One might, however, question if this is correct. Surely, if A is logically possible, then logic will deem that it is so by necessity. Could one, therefore, add to either of these logics to get also the S5 principle
Translating this to the equivalent formula using \(\mathbf{t} \) instead of \(\Box \), one gets the formula  , which can be read “if it’s not the case that A is entailed by logic, then logic entails that A is not entailed by logic. Adding (5) to Æ does not yield M, nor does it yield R if added to E. As in ordinary modal logic, one could equivalently add the B axiom \(A \rightarrow \Box \Diamond A\) which has a more natural read to it: if A is true, then logic entails that it is not the case that
, which can be read “if it’s not the case that A is entailed by logic, then logic entails that A is not entailed by logic. Adding (5) to Æ does not yield M, nor does it yield R if added to E. As in ordinary modal logic, one could equivalently add the B axiom \(A \rightarrow \Box \Diamond A\) which has a more natural read to it: if A is true, then logic entails that it is not the case that  is entailed by logic. It is therefore best interpreted as a strong consistency principle. By using the contraposition axiom it is easy to see that \(A \rightarrow \Box \Diamond A\) is in fact interderivable with \(A \rightarrow ((A \rightarrow \mathbf{f} ) \rightarrow \mathbf{f} )\) which is an instance of the assertion axiom. Adding the full assertion axiom, \(A \rightarrow ((A \rightarrow B) \rightarrow B)\), is in fact equivalent to adding the modality-trivializer \(A \rightarrow \Box A\), which therefore punctures the modal reading of being entailed by \(\mathbf{t} \), and therefore the modal character of the logics. R and M, which are obtained by adding full assertion to, respectively, E and Æ, are therefore akin to the modally trivial logic called Triv in Hughes and Cresswell (1996).
is entailed by logic. It is therefore best interpreted as a strong consistency principle. By using the contraposition axiom it is easy to see that \(A \rightarrow \Box \Diamond A\) is in fact interderivable with \(A \rightarrow ((A \rightarrow \mathbf{f} ) \rightarrow \mathbf{f} )\) which is an instance of the assertion axiom. Adding the full assertion axiom, \(A \rightarrow ((A \rightarrow B) \rightarrow B)\), is in fact equivalent to adding the modality-trivializer \(A \rightarrow \Box A\), which therefore punctures the modal reading of being entailed by \(\mathbf{t} \), and therefore the modal character of the logics. R and M, which are obtained by adding full assertion to, respectively, E and Æ, are therefore akin to the modally trivial logic called Triv in Hughes and Cresswell (1996).
Definition 10
(The Brouwerian axiom) \(\mathbf{L5} \) is hereby defined as the logic L augmented with
Theorem 2
The necessitation rule is not derivable either \(\mathbf{E} {} \mathbf{5} \), \(\mathbf{E} ^\mathbf{t} \mathbf{5} \) or Æ5.
Proof
The counter-model in Fig. 1 to the rule \(\{A\} \vdash ^h \mathbf{t} \rightarrow A\) also validates (B) as is easy to verify, and since also \(\llbracket \Box A \rrbracket = \llbracket \mathbf{t} \rightarrow A\rrbracket \) in that model, the result follows. \(\square \)
At the very end of Ackermann (1956), a model for Ackermann’s logic \({\Pi '}\) is presented which falsifies any formula \(A \rightarrow (B \rightarrow C)\) where B and C are arbitrary, but A is built up solely from  . Since E is a sublogic of Ackermann’s logic, neither it has any theorems on this form. The defining B-axiom is on this form, and so the property does not extend to E5. It does, however extend to Æ as the following theorem shows:
. Since E is a sublogic of Ackermann’s logic, neither it has any theorems on this form. The defining B-axiom is on this form, and so the property does not extend to E5. It does, however extend to Æ as the following theorem shows:
Theorem 3
Æ has the Ackermann property, i.e. it does not have any theorems on the form \(A \rightarrow (B \rightarrow C)\) for A’s over the  -fragment of the language.
-fragment of the language.
Proof
It is easy to verify that \(\mathbf{t} \wedge \mathbf{f} \rightarrow A\) holds in Ackermann’s model to be found in Ackermann(1956, p. 127).Footnote 12\(\square \)
Corollary 1
E and Æ are modally nice.
5 Conservative extension results
It was shown in Øgaard (2019, thm. 5) that both Ackermann’s logic \({\Pi '}\) as well as \({\Pi '}_{\!\!\mathbf{E} }\) extend classical logic; they both validate all the logical theorems of classical logic over the \(\rightarrow \)-restricted language, but also validate every classically valid rule involving  and \(\wedge \). That property is easily seen to extend to the (Ax18)-logics presented in this paper. Since \(\mathbf{E} ^\mathbf{t} \), Æ, \(\mathbf{E} ^\mathbf{t} \mathbf{5} \) and Æ5 are modal logics one may wonder if these logics extend the classical modal logics S4 and S5. This section shows first that M is a conservative extension of R and then that Æ(Æ5) is a not conservative extension of E(E5). The trade-off with regards to the latter result is that Æ(Æ5) turns out to interpret S4(S5) on the most natural interpretation, where any formula \(\blacksquare A\) of S4(S5) is translated to the Æ(Æ5)-formula \(\Box A\).Footnote 13
and \(\wedge \). That property is easily seen to extend to the (Ax18)-logics presented in this paper. Since \(\mathbf{E} ^\mathbf{t} \), Æ, \(\mathbf{E} ^\mathbf{t} \mathbf{5} \) and Æ5 are modal logics one may wonder if these logics extend the classical modal logics S4 and S5. This section shows first that M is a conservative extension of R and then that Æ(Æ5) is a not conservative extension of E(E5). The trade-off with regards to the latter result is that Æ(Æ5) turns out to interpret S4(S5) on the most natural interpretation, where any formula \(\blacksquare A\) of S4(S5) is translated to the Æ(Æ5)-formula \(\Box A\).Footnote 13
Definition 11
(Conservative Extension) If \(\mathbf{L} _1\) and \(\mathbf{L} _2\) are logics over, respectively, languages \({\mathcal {L}}_1\) and \({\mathcal {L}}_2\) such that \({\mathcal {L}}_1 \subseteq {\mathcal {L}}_2\), then \(\mathbf{L} _2\) conservatively extends \(\mathbf{L} _1\) if \(\varnothing \vdash _\mathbf{L _1} A\) for every \({\mathcal {L}}_1\)-formula A such that \(\varnothing \vdash _\mathbf{L _2} A\).
Theorem 4
M is a conservative extension of R.
Proof
Meyer and Routley showed in (1974) that R is conservatively extended by Boolean negation. Furthermore, R with both Boolean negation and \(\mathbf{t} \) added—\(\mathbf{CR} ^\mathbf{t} \)—is a conservative extension of R (Giambrone and Meyer 1989, thm. 7). Thus if \(\varnothing \vdash ^h_\mathbf{CR ^\mathbf{t }} A\), for any formula A over the logical connectives  , then \(\varnothing \vdash ^h_\mathbf{R } A\). Furthermore, \(A \rightarrow \mathbf{t} \vee \mathbf{f} \) is derivable in this logic (Øgaard 2020b, Lemma 3.3), from which it is easy to derive (Ax18). \(\top \) can in fact be defined in CR simply as \(p \vee \lnot p\) for some propositional variable p, where \(\lnot \) is the Boolean negation. Thus if \(\varnothing \vdash ^h_\mathbf{M } A\), for any formula A over the logical connectives
, then \(\varnothing \vdash ^h_\mathbf{R } A\). Furthermore, \(A \rightarrow \mathbf{t} \vee \mathbf{f} \) is derivable in this logic (Øgaard 2020b, Lemma 3.3), from which it is easy to derive (Ax18). \(\top \) can in fact be defined in CR simply as \(p \vee \lnot p\) for some propositional variable p, where \(\lnot \) is the Boolean negation. Thus if \(\varnothing \vdash ^h_\mathbf{M } A\), for any formula A over the logical connectives  , then \(\varnothing \vdash ^h_\mathbf{CR ^\mathbf{t }} A\), and therefore \(\varnothing \vdash ^h_\mathbf{R } A\). \(\square \)
, then \(\varnothing \vdash ^h_\mathbf{CR ^\mathbf{t }} A\), and therefore \(\varnothing \vdash ^h_\mathbf{R } A\). \(\square \)
Mares showed in (2000) that E is not conservatively extended by Boolean negation by showing that the extensional K-sentence \(\Box (A \supset B) \supset (\Box A \supset \Box B)\), for a certain restricted class of formulas A and B, is a theorem of CE, but not of E. His result carries over to Æ as the following theorem shows:
Theorem 5
Æ is not a conservative extension of E and neither is Æ5 a conservative extension of E5.
Proof
This follows from the proof given in Øgaard (2020a, thm. 7) of Mares’ result that CE is not a conservative extension of E since both Æ and Æ5 are axiomatic extensions of E for which \(\gamma \), i.e.  , is a derivable rule. \(\square \)
, is a derivable rule. \(\square \)
How concerned should one be by the fact that Æ does not conservatively extend E? One ought to care that an extension is not conservative if one has reasons for thinking that the original logic got everything right with regards to that part of the language. However, if one has reasons for thinking that the original logic is incomplete, then simply proving a non-conservativeness result may not tell against the extension as one may have independent reasons for thinking that the surplus generated are indeed correct principles of logic. I will not go into depth with regards to the reasons for thinking that E is modally incomplete, save to point out that this is by far not a new idea: noting that the extensional K-sentence fails not only for E, but also for NR—R with a S4-modality added—Routley and Meyer (1972, p. 70) suggested (from a suggestion by Belnap) that both these logics should be augmented by the axiom of modal confinement, \(\Box (A \vee B) \rightarrow (\Diamond A \vee \Box B)\).Footnote 14Æ fails to validate this stronger axiom, and so may as well be argued to be modally incomplete. Note, however, that it does validate the enthymematical version of it, namely \(\Box (A \vee B) \mapsto (\Diamond A \vee \Box B)\). Of course, there may be other consequences of adding (Ax18) to E, but I take it, then, that Mares’ result does not on its own show that the non-conservativeness of Æ over E results in something which is undesirable.
We have seen that both E and Æ are S4 modal logics, and since they extend classical logic—theorem-wise in the case of E and inferentially in the case of Æ—it is a welcomed fact that Æ interprets S4 in the most natural way possible, and disappointing that E does not. Although there are translations on which Et in fact interprets S4 exactly, these are non-direct translation. The nice feature of the direct translation is that the theory of entailment and that of modality are connected so that being necessarily true and entailed by logic are equivalent notions: that is that \(\Box A \leftrightarrow (\mathbf{t} \rightarrow A)\) is a logical truth.Footnote 15
Æ not only extends classical logic in that every valid rule of classical logic, including the meta-rule reasoning by cases,Footnote 16 is valid in Æ, but it also interprets S4 in its extensional fragment plus \(\Box \). It validates every S4 axiom expressed with \(\rightarrow \) as well as with \(\supset \), and makes the necessitation rule admissible yet not derivable, precisely as it indeed should be. That Æ is not a conservative extension of E may have other consequences than \(\Box (A \supset B) \supset (\Box A \supset \Box B)\) being a logical theorem of Æ. Such other consequences may prove to be undesirable. However, Mares’ result in itself does not point to any such.
Note that \((A \rightarrow B) \rightarrow (A \supset B)\) is a theorem of any of our logics since all logics in this paper includes (Ax12),  . It therefore follows that \(\Diamond A \supset \Box \Diamond A\) is a theorem of both \(\mathbf{E} ^\mathbf{t} \mathbf{5} \) and Æ5. Since Æ interprets classical modal logic S4 and \(\Diamond A \supset \Box \Diamond A\) is a theorem of Æ5, it therefore follows that that Æ5 interprets classical modal logic S5 under the natural translation.
. It therefore follows that \(\Diamond A \supset \Box \Diamond A\) is a theorem of both \(\mathbf{E} ^\mathbf{t} \mathbf{5} \) and Æ5. Since Æ interprets classical modal logic S4 and \(\Diamond A \supset \Box \Diamond A\) is a theorem of Æ5, it therefore follows that that Æ5 interprets classical modal logic S5 under the natural translation.
6 Variable sharing for logics with truth-constants
The variable sharing property was put forward in Belnap (1960a) as a way to spell out the requirement of relevance between antecedent and consequent in a logically true conditional:
Confining our attention to propositional logic, a partial solution becomes almost obvious once we note that in propositional logic, commonality of meaning is carried by identity of propositional variables. Thus, for A to be relevant to B in the required sense, a necessary condition is that A and B have some propositional variable in common. (Belnap 1960a, p. 144)
Definition 12
(Variable sharing property) A logic L without truth-constants has the variable sharing property just in case for every formula A and B, \(\varnothing \vdash _\mathbf{L } A \rightarrow B\) only if A and B share a propositional variable.
The variable sharing property does, by definition, not apply to logics with truth-constants. Even if one were to change the definition of the property so as not to exclude logics with truth-constant by default, such logics seem to blatantly violate any notion of variable sharing as, for instance, the following formulas are all theorems of even \(\mathbf{E} ^\mathbf{t \top }\):

Both \(\mathbf{t} \) and \(\top \) are quite freely made use of by relevant logicians and so the question arises if the variable sharing property can in any legitimate sense be extended to cover logics with \(\mathbf{t} \) and \(\top \). There are two suggestions in the literature for how to address this question. The most common practice is to ascribe the variable sharing property to any logic just in case the property holds for all constant free formulas. This is, for instance, how the variable sharing property is stated in Galatos et al. (2007, p. 253).
Definition 13
(Constant-weak VSP) A logic L has the constant-weak variable sharing property just in case for every truth-constant free formula A and B, \(\varnothing \vdash ^h_\mathbf{L } A \rightarrow B\) only if A and B share a propositional variable.
Theorem 6
\(\mathbf{E} ^\mathbf{t \top }\), Æ, \(\mathbf{R} ^\mathbf{t \top }\) and M, all have the constant-weak variable sharing property.
Proof
This follows by noting that all the axioms and rules of M, and therefore all the three other logics as well, hold true in Belnap’s test-model for relevance.Footnote 17\(\square \)
The another approach to the variable sharing property for logics with truth-constants, was presented in Yang (2013). Yang’s idea, developed, according to himself, from an idea of Beall and Restall (2005), is that one should not simply disregard the presence of the truth-constants, but rather demand that variable sharing should occur under the intended interpretation of the truth-constants.
Definition 14
(Constant-strong VSP) A logic L has the constant-strong variable sharing property just in case for every truth-constant free formula A and B, \(\varnothing \vdash ^h_\mathbf{L } A \rightarrow B\) only if either A and B share a propositional variable, or they do so in light of the intended interpretation of \(\mathbf{t} \) and \(\top \) as, respectively, the conjunction of every logical truth and the disjunction of every sentence.
(a) does not violate this strong variable sharing property since \(\mathbf{t} \), being the conjunction of every logical truth, has \(A \rightarrow A\) as one of its conjunctions, and so  shares a propositional variable in light of the interpretation of \(\mathbf{t} \).Footnote 18 The same type of explanation goes for (b)–(d). Now consider an instance of (Ax18) with A as the consequent—\(\mathbf{t} \wedge \mathbf{f} \rightarrow A\). Since \(\mathbf{t} \) is the conjunction of every logical truth, it will have \(A \rightarrow A\) as one of its conjunctions, and so the antecedent and consequent share a propositional variable Futhermore, just as neither \(A \rightarrow \top \) nor \(\top \rightarrow A\) violates the constant-strong variable sharing property, nor does \(\mathbf{t} \rightarrow A\). It therefore seems hard to distinguish these two variants of the variable sharing property. Indeed the following theorem shows that they are equivalent.
shares a propositional variable in light of the interpretation of \(\mathbf{t} \).Footnote 18 The same type of explanation goes for (b)–(d). Now consider an instance of (Ax18) with A as the consequent—\(\mathbf{t} \wedge \mathbf{f} \rightarrow A\). Since \(\mathbf{t} \) is the conjunction of every logical truth, it will have \(A \rightarrow A\) as one of its conjunctions, and so the antecedent and consequent share a propositional variable Futhermore, just as neither \(A \rightarrow \top \) nor \(\top \rightarrow A\) violates the constant-strong variable sharing property, nor does \(\mathbf{t} \rightarrow A\). It therefore seems hard to distinguish these two variants of the variable sharing property. Indeed the following theorem shows that they are equivalent.
Theorem 7
The constant-weak and constant-strong variable sharing properties are coextensive.
Proof
Having the constant-strong property obviously entails having the constant-weak one. Assume that L is a logic which has the constant-weak variable sharing property and let \(A \rightarrow B\) be any logical theorem of L. Now if \(\mathbf{t} \) or \(\top \) are subformulas of A (B), then since every formula \(p \rightarrow p\) is part of the intended reading of both \(\mathbf{t} \) and \(\top \), A (B) will contain every propositional variable on the intended reading of the truth-constants, and so will share at least one with B (A). If neither truth-constants occur in \(A \rightarrow B\) then as the logic has the constant-weak variable sharing property it follows that A and B actually share a propositional variable. \(\square \)
So both Æ and M have the same variable sharing properties as the paraconsistent siblings \(\mathbf{E} ^\mathbf{t \top }\) and \(\mathbf{R} ^\mathbf{t \top }\). This is far from trivial as it is quite easy to extend a logic with axioms for a truth-constant in such a way as to make the logic loose its variable sharing property; one could, for instance, add \(\top \rightarrow (A \rightarrow A)\) to \(\mathbf{E} ^\top \) which on its own does not violate the variable sharing property, but which begets the theorem \(B \rightarrow (A \rightarrow A)\) which evidently does.
Meyer famously wanted to extend R with Boolean negation, \(\lnot \), to CR, and argued that the fact that one may do so conservatively, shows that the extension is legitimate (Meyer 1974). CR is simply R strengthened by the two Boolean axioms \(A \wedge \lnot A \rightarrow B\) and \(A \rightarrow B \vee \lnot B\). CR, however, only has the variable sharing property provided one restricts this to the Boolean-free fragment. As we have seen in this section, no such restriction is needed in the case of either Æ, Æ5 or M beyond the clauses needed to wiggle room for the truth-constants; wiggling one has to do also in the case of \(\mathbf{E} ^\mathbf{t \top }\), \(\mathbf{E5} ^\mathbf{t \top }\) and \(\mathbf{R} ^\mathbf{t \top }\).
Just as constant-enriched relevant logics such as M satisfy a constant-weak variable sharing property, Boolean relevant logics such as Meyer’s CR satisfy a \(\lnot \)-weak variable sharing property. One might therefore wonder if there is also a corresponding \(\lnot \)-strong variable sharing property? One could, as mentioned in Restall (1999, fn. 18), argue that there is an implicit \(\bot \) lurking in the Boolean negation of A; \(A \wedge \lnot A \rightarrow B\) might not violate the variable sharing property just as neither \(A \wedge (A\rightarrow \bot ) \rightarrow B\) does. This might be possible, but such an interpretation should then be independently justifiable, and ought to differentiate between \(\lnot A\) and \(A \rightarrow \bot \) since these two negations are not equivalent even in CR. The truth-constants, on the other hand, have natural interpretations which are justifiable independent of concerns over variable sharing.
7 Enthymemes, deduction theorems and rule normality
This section discusses A&B’s view of two criteria for theory choice, namely having an enthymematic conditional for which a deduction theorem holds, and having the property of rule normality. These properties are not intended as relevance-properties, but rather as more general adequacy-conditions on a theory of logical consequence. It is shown that Æ and M satisfy both these criteria in the same manner as \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \) do. The logics \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\)—\(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \) with \((\gamma )\) added as a primitive rule—however, are not rule normal. It is shown, however, that even though they do not satisfy the enthymematical deduction theorem with regards to the conditional \(\mapsto \), one can define a different conditional for which a deduction theorem is provable.
In Øgaard (2019, thm. 7–8) I showed that the logic \({\Pi '}_{\!\!\mathbf{E} }\) has the following two deduction theorems:
Axioms here is some finite conjunction of axioms of the logic in question. The first does not hold for either E and R since disjunctive syllogism, i.e. modus ponens for \(\supset \), is not derivable in these logics, although the theorem does hold if this rule is added. That the latter holds for E and R is well known. Inspecting the proofs in Øgaard (2019) will easily convince the reader that both also apply to Æ and M. However, without \(\mathbf{t} \), there is no way of replacing Axioms uniformly by a particular formula. Using \(\mathbf{t} \), however, we can define the enthymematic conditional \(\mapsto \), where \(A\mapsto B =_{df} A \wedge \mathbf{t} \rightarrow B\), for which a uniform deduction theorem holds:
Theorem 8
(\(\mathbf{t} \)-enthymematic deduction theorem) Let L be any axiomatic extension of \(\mathbf{E} ^\mathbf{t} \) for which the rule \(\{A \}\vdash ^h \mathbf{t} \rightarrow A\) is at least admissible, then
Proof
The proof is given in detail in the appendix. A sketch of the proof was to my knowledge first given in Meyer (1970, p. 183). \(\square \)
Corollary 2
The \(\mathbf{t} \)-enthymematic deduction theorem holds for all of \(\mathbf{E} ^\mathbf{t} \), \(\mathbf{E5} ^\mathbf{t} \), \(\mathbf{R} ^\mathbf{t} \), as well as their \(\top \)-extension, and Æ, Æ5 and M.
Notice that the \(\mathbf{t} \)-enthymematic deduction theorem can’t be liberalized to read
since the rule \(\{A\} \vdash ^h \mathbf{t} \rightarrow A\) is only assumed to be admissible. Reading the proof carefully, however, it is easily seen that if the rule is derivable, then the theorem can be so liberalized. We therefore have the following:Footnote 19
Corollary 3
The liberalized \(\mathbf{t} \)-enthymematic deduction theorem holds for \(\mathbf{R} ^\mathbf{t} \), \(\mathbf{R} ^\mathbf{t \top }\) and M.
I noted above that adding \((\gamma )\) to E or R suffices for yielding the \(\supset \)-deduction theorem. However, just as the Axioms-variant of the deduction theorem fails for both E or R with \((\gamma )\) added as shown in Øgaard (2019, thm. 8), so does the \(\mathbf{t} \)-enthymematic deduction theorem fail for both \(\mathbf{E} ^\mathbf{t }[\gamma ]\) and \(\mathbf{R} ^\mathbf{t }[\gamma ]\):
Theorem 9
The \(\mathbf{t} \)-enthymematic deduction theorem fails for both \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\)
Proof
Note that both these logics validate the rule  . The model in Fig. 2 is a model for \(\mathbf{R} ^\mathbf{t} [\gamma ]\) in which \(\mathbf{t} \) is assigned the value 2. The model, however, fails to validate (Ax18)—\(\mathbf{t} \wedge \mathbf{f} \rightarrow A\) is assigned 0 when A is assigned to 0—and therefore shows that the enthymematic deduction theorem fails for both logics. \(\square \)
. The model in Fig. 2 is a model for \(\mathbf{R} ^\mathbf{t} [\gamma ]\) in which \(\mathbf{t} \) is assigned the value 2. The model, however, fails to validate (Ax18)—\(\mathbf{t} \wedge \mathbf{f} \rightarrow A\) is assigned 0 when A is assigned to 0—and therefore shows that the enthymematic deduction theorem fails for both logics. \(\square \)
In discussing Ackermann’s logic \({\Pi '}\), Anderson et al. (1992, § 45.2) note that it can in fact be axiomatized as \(\mathbf{E} [\gamma ]\).Footnote 20 With regards to \((\gamma )\) , then, they note that the
addition of \((\gamma )\) as a primitive to E destroys practically every nice property E has. [...] Most of the metalogical proofs are by induction on the length of formal proofs in E, and, in the absence of \( A \& ({\overline{A}}\vee B) \rightarrow B\), there is apparently no way of getting over the inductive step where \((\gamma )\) is used.
This fact led to the observation that, if \( A \& ({\overline{A}}\vee B) \rightarrow B\) does not belong in a theory of entailment, which it obviously (by this time) does not, then the primitive rule \((\gamma )\) does not belong there either. (Anderson et al. 1992, pp. 138f)
It is rather unclear what these “nice” properties of E are. Note first of all that it follows from Meyer and Dunn (1969)’s proof that \((\gamma )\) is admissible not only in E and R, but also in \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \). Thus for all these logics it is the case that \(\varnothing \vdash ^h_\mathbf{L } A\) if and only if \(\varnothing \vdash ^h_\mathbf{L [\gamma ]} A\). We shall see in the next section that A&B’s notion of entailment viewed as a consequence relation can be modified every so slightly so as to yield the Entailment theorem provable also for \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\), as well as their \(\mathbf{t} \)-free variants. Thus the Entailment theorem is not one of the “nice” properties. Nor is the variable sharing property a “nice” property seeing as it is even noted in Belnap (1960a, fn. 3) that it holds for \({\Pi '}\). It seems, then, that the only “nice” property that \(\mathbf{E} ^\mathbf{t} \) has, but which \(\mathbf{E} ^\mathbf{t} [\gamma ]\) does not, is the enthymematical deduction theorem.
Note, then, that both \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\) satisfy an alternative form of the enthymematic deduction theorem. According to Bimbó and Dunn (2018), Maksimova proved in her 1966 Russian article Formal deductions in the calculus of rigorous implication (Maksimova 1966) that

where \(P_n\) is the conjunction of every \(p \rightarrow p\) such that the propositional variable p occurs in \(\varGamma \cup \{A\}\) and \(\varGamma \) consists only of \(\rightarrow \)-formulas. Meyer defined in Meyer (1970) the enthymematic conditional \(\hookrightarrow \), where \(A \hookrightarrow B =_{df} A \wedge \mathbf{t} \rightarrow \mathbf{f} \vee B\). Using Maksimova’s idea and Meyer’s enthymematic conditional, then, we state the following result:
Theorem 10
(\(\mathbf{t} /\mathbf{f} \)-enthymematic deduction theorem) Let L be any axiomatic extension of \(\mathbf{E} ^\mathbf{t} [\gamma ]\) for which the rule \(\{A\} \vdash ^h \mathbf{t} \rightarrow A\) is at least admissible, then
Proof
The proof is given in the appendix. \(\square \)
Corollary 4
(\(\mathbf{t} /\mathbf{f} \)-enthymematic deduction theorem) Let L be either \(\mathbf{E} ^\mathbf{t} \) or \(\mathbf{R} ^\mathbf{t} \), then
Proof
\((\gamma )\) is, as noted above, admissible for both \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \), and so
The result now follows using Thm. 10. \(\square \)
The bibliography of Anderson et al. (1992) lists the mentioned article by Maksimova, although her result is not mentioned in either Anderson and Belnap (1975) or Anderson et al. (1992). They do, however, discuss a conditional quite closely related to \( \hookrightarrow \). Note, first of all, that it is not only the material conditional which is regarded as “no kind of conditional”; also the strict conditional of S4,  , fails to be a proper conditional, according to A&B, since, again, modus ponens fails for it (cf. Anderson and Belnap 1975, p. 260). Interestingly, though, they do accept that if only S4 is formulated with
, fails to be a proper conditional, according to A&B, since, again, modus ponens fails for it (cf. Anderson and Belnap 1975, p. 260). Interestingly, though, they do accept that if only S4 is formulated with  primitive, then its positive fragment, S4\(^+\), harbors a proper conditional. Similarly, they do accept that the intuitionist conditional is a proper conditional. These conditionals fall short of representing entailment since they do validate implicational paradoxes—for instance \(A \rightsquigarrow (B \rightsquigarrow B)\) is a logical truth of both intuitionist logic and S4\(^+\) (where \(\rightsquigarrow \) is, respectively, the intuitionistic and strict conditional).Footnote 21 Although shy of being entailment conditionals, these conditionals are regarded by A&B as enthymematical conditionals. Such conditionals can be regarded, according to A&B, as representing if ...then __-locutions of natural language. They are not, however, to be read as that A entails that B, which is A&B’s preferred reading of the E-formula \(A \rightarrow B\) (cf. Anderson and Belnap 1975, A5), but rather as that \(A \wedge r\) entails that B, where r is some true statement:
primitive, then its positive fragment, S4\(^+\), harbors a proper conditional. Similarly, they do accept that the intuitionist conditional is a proper conditional. These conditionals fall short of representing entailment since they do validate implicational paradoxes—for instance \(A \rightsquigarrow (B \rightsquigarrow B)\) is a logical truth of both intuitionist logic and S4\(^+\) (where \(\rightsquigarrow \) is, respectively, the intuitionistic and strict conditional).Footnote 21 Although shy of being entailment conditionals, these conditionals are regarded by A&B as enthymematical conditionals. Such conditionals can be regarded, according to A&B, as representing if ...then __-locutions of natural language. They are not, however, to be read as that A entails that B, which is A&B’s preferred reading of the E-formula \(A \rightarrow B\) (cf. Anderson and Belnap 1975, A5), but rather as that \(A \wedge r\) entails that B, where r is some true statement:
the “if ...then __” proposition corresponding to any enthymematic argument is true if and only if there is a (suppressed) premiss which is true and which would convert the enthymeme into a valid argument. (Anderson et al. 1992, p. 50)
The intuitionist conditional, according to A&B, allows one to “suppress” any such merely true r, whereas S4 allows one to suppress any necessarily true r. I will in the following only focus on so-called strict enthymemes, and thus disregard the intuitionist conditional.
A&B rendered  —the strict conditional—in E using propositional quantifiers. Thus they define
—the strict conditional—in E using propositional quantifiers. Thus they define  as \(\exists r(\Box r \wedge (r \wedge A \rightarrow B))\). A&B note that the fragment of E augmented with propositional quantifiers—\(\mathbf{E} ^{\forall \exists p}\)—which contains formulas using only \(\wedge \) and \(\vee \) as well as the defined connective
as \(\exists r(\Box r \wedge (r \wedge A \rightarrow B))\). A&B note that the fragment of E augmented with propositional quantifiers—\(\mathbf{E} ^{\forall \exists p}\)—which contains formulas using only \(\wedge \) and \(\vee \) as well as the defined connective  , “exactly coincides with the positive fragment of Lewis’s system S4 of strict implication” (Anderson et al. 1992, p. 52). The reason, they claim, that one has to restrict to the positive fragment is that S4 validates the “irrelevant” theorem
, “exactly coincides with the positive fragment of Lewis’s system S4 of strict implication” (Anderson et al. 1992, p. 52). The reason, they claim, that one has to restrict to the positive fragment is that S4 validates the “irrelevant” theorem  :
:
If we tried to explain away this modal curiosity by treating it as a strict enthymeme in \(\mathbf{E} ^{\forall \exists p}\) in the sense given above, it would come to
which has a decidedly irrelevant appearance in \(\mathbf{E} ^{\forall \exists p}\) [...].
We can, however, find a different strict enthymematic “implication” that does the job of embedding all of S4, including its negation, in \(\mathbf{E} ^{\forall \exists p}\): we can show that defining
by
catches all and only the theorems of S4 in \(\mathbf{E} ^{\forall \exists p}\). This result of Meyer [...] is not, however, as interesting as the foregoing positive result in relation to our particular project, because this second account of the hook is given in terms of only and “implication” and not an implication: in absolute contrast to our positive enthymematic implications, it would be as much a fallacy to suppose that detachment held for the definiens displayed above as it would be to suppose that detachment held for material “implication”. (Anderson et al. 1992, p. 53)
The work by Meyer A&B referred to was Meyer (1970). In it, Meyer showed both that A&B’s official definition of  can be rendered using the Ackermann constant, namely as \(A \mapsto B =_{df} A \wedge \mathbf{t} \rightarrow B\), and that the strict enthymematic “implication” can be rendered using \(\hookrightarrow \).
can be rendered using the Ackermann constant, namely as \(A \mapsto B =_{df} A \wedge \mathbf{t} \rightarrow B\), and that the strict enthymematic “implication” can be rendered using \(\hookrightarrow \).
Notice first of all that even though one might agree with A&B that

may look like a statement which amounts to a relevant fallacy, looks can be deceiving. Rendering it using \(\mapsto \) yields  which is a logical theorem of Æ and Æ satisfies, or so this paper tries to show, every relevant property that \(\mathbf{E} ^\mathbf{t} \) does.
which is a logical theorem of Æ and Æ satisfies, or so this paper tries to show, every relevant property that \(\mathbf{E} ^\mathbf{t} \) does.
With regards to \(\hookrightarrow \), note that A&B’s comments amounts to reject that modus ponens holds for it, although I take their comment to imply that they regard \(\mapsto \) to be a conditional for which modus ponens holds. That is, the argument from A and \(A \mapsto B\) to B is valid, according to A&B. However, the sense in which it is valid is itself enthymematic: \((A \wedge (A \mapsto B)) \mapsto B\) is a logical truth of \(\mathbf{E} ^\mathbf{t} \), although \((A \wedge (A \mapsto B)) \rightarrow B\) is not. Just after noting that “\({\overline{A}} \vee B\) is no kind of conditional, since modus ponens fails for it, as we have remarked ad nauseam before,” A&B go on
[t]o console the reader who thinks we have gone completely out of our minds we note that there is a connective, namely the enthymematic implication of § 35, for which both the Official deduction theorem and modus ponens holds.Footnote 22 The existence of such an “if ...then —,” one which we have often used in this book, and indeed one could hardly get along without (think of what it would be like always to state all the premisses for your argument), probably accounts, in part, anyway, for the attractiveness of the view that the Official deduction theorem has something to do with “if ...then —.” (Anderson and Belnap 1975, p. 259)
I take it, then, that A&B do regard having at least one conditional for which an enthymematic deduction theorem holds is of utmost importance. It is, however, important to note that A&B nowhere indicate that having such a conditional is itself to be viewed as a relevance criterion. Rather, I suggest, that it be viewed as an adequacy criterion on the theory of entailment pertaining to expressive strength. In light of Maksimova’s result for \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and the \(\mathbf{t} \)-version of it provided here, it seems that \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\) do satisfy A&B’s requirement of having an enthymematic conditional seeing as \(\hookrightarrow \) has exactly the same properties in \(\mathbf{E} ^\mathbf{t} [\gamma ]\)(\(\mathbf{R} ^\mathbf{t} [\gamma ]\)) as \(\mapsto \) has in \(\mathbf{E} ^\mathbf{t} \)(\(\mathbf{R} ^\mathbf{t} \)). It seems, then, that having a conditional for which the enthymematical deduction theorem holds isn’t a “nice” property either.
There is, however, one “nice” property that \(\mathbf{E} ^\mathbf{t} \)(\(\mathbf{R} ^\mathbf{t} \)) has, but which \(\mathbf{E} ^\mathbf{t} [\gamma ]\)(\(\mathbf{R} ^\mathbf{t} [\gamma ]\)) lacks, namely rule normality:
Definition 15
(Rule normality) A logic L satisfies rule normality just in case for every primitive rule \(\{A_1, \ldots , A_n\} \Vdash B\) of L, \(\varnothing \vdash ^h_\mathbf{L } A_1 \wedge \ldots \wedge A_n \rightarrow B\)
Note, then, that Æ and M also satisfy this “nice” property, but that \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\) do not. The criterion of rule normality can be found in Belnap (1960b, p. 12).Footnote 23 Belnap lists this property as one of in total ten “mandatory” conditions on an adequate theory of entailment. One can, however, only speculate as to Belnap’s reason for demanding rule normality as he never gives an argument for why it is mandatory. Note, then, that rule normality is not explicitly stated as a general requirement in either Anderson and Belnap (1975) or Anderson et al. (1992). Rule normality is mentioned in Anderson and Belnap (1975) in connection with the necessitation rule. A&B think that the rule \(\{A\} \Vdash \Box A\) should in the case of E be admissible for the consequence relation \(\vdash ^h\). Many modal logics are formulated with a primitive admissible rule, something like \(\varnothing \vdash ^h A \Rightarrow \varnothing \vdash ^h \Box A\). A&B, however, say that such a “non-normal [rule], in the sense that the corresponding implication \(A \rightarrow \Box A\) is not a theorem, [...] [yields a system which] lacks elegance.” (Anderson and Belnap 1975, p. 117). They even liken having such a primitive admissibility rule of necessity to having simply \(A \rightarrow \Box A\) as a theorem:
Both courses are equally odious, the latter because it destroys the notion of necessity, and the former because, if \(A \rightarrow \Box A\) is neither true nor a theorem, then we ought not to have — in a coherent formal account of the matter — a primitive rule to the effect that \(\Box A\) does after all follow from A. (Anderson and Belnap 1975, p. 235)
This latter quote, then, seems to indicate that A&B did accept rule normality as a selection criteria.Footnote 24 Undoubtedly, however, rule normality does not either belong in the category of relevance-properties, although it may very well be listed as a more general adequacy condition on a theory of entailment seeing as it yields that every primitive rule yields a true entailment. Even if it is deemed a necessary condition for an adequate theory of entailment as A&B seem to think, however, such a theory need not rule the material conditional a conditional non grata seeing as both Æ and M are rule normal.
We have in this section seen that the enthymematical deduction theorem holds for Æ and M in precisely the same manner for which it holds for \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \), namely where the deduction theorem is stated using \(\mapsto \), where \(A \mapsto B =_{df} A \wedge \mathbf{t} \rightarrow B\). This, we saw, was not the case for \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\). However, we saw that these logics do have an enthymematical deduction theorem only relative to a different enthymematic conditional, namely the conditional \(A \hookrightarrow B =_{df} A \wedge \mathbf{t} \rightarrow \mathbf{f} \vee B\). We saw that A&B did acknowledge \(\mapsto \) as a proper conditional, but that they denied that \(\hookrightarrow \) was a proper conditional on account of it, like the material conditional, didn’t satisfy modus ponens. Note, then, that modus ponens holds for \(\hookrightarrow \) if and only if it holds for the material conditional. Modus ponens does not hold for the material conditional in E; however, this section has made it clear that ruling the material conditional to be “no kind of conditional” (Anderson and Belnap 1975, p. 259) using either the requirement of an enthymematic deduction theorem, or rule normality, is unfounded. The next section looks into the use-criterion for relevance, that, intuitively, A does not entail B unless any proof of B from A must use A. We will see that neither it can be used to rule the material condition a non-conditional.
8 The Entailment theorem
We have so far seen that Æ and M have the same variable sharing property as \(\mathbf{E} ^\mathbf{t \top }\) and \(\mathbf{R} ^\mathbf{t \top }\) do. The other relevance property presented by A&B was meant to capture a notion of premise use, that the conclusion ought to follow from the premisses; the thought being roughly that if the conclusion follows without using the premises, then it doesn’t really follow from them. This notion of following from is not captured in the Hilbertian notion of logical consequence: even for logics like E it is the case that \(B \rightarrow B\) follows logically from an arbitrary formula A: \(\{A\} \vdash ^h_\mathbf{E } B \rightarrow B\).
As mentioned in the introduction, A&B sought to find not only a new entailment-conditional, but one such which could be read as expressing a new notion of logical consequence altogether: the consequence relation called entailment by A&B and which their entailment-conditional \(\rightarrow \) was meant to express. Since, however, the consequence relation is definable for logics which are not thought of as expressing entailment—the conditional of R, for instance, is rather to be thought of as a demoalized version of E’s \(\rightarrow \) expressing rather a contingent notion of logical consequence referred to as simply relevant implication—I will rather call the consequence relation relevant.Footnote 25
Given any conditional \(\multimap \) and a consequence relation \(\unrhd \) relating, as the Hilbertian one does, sets of formulas to single formulas, one may define a new consequence relation \(\rhd \) simply by letting \(\varGamma \rhd B\) if and only if there exists a set \(\{A_1, \ldots , A_n\}\subseteq \varGamma \) such that \(\varnothing \unrhd \bigwedge _{i\le n} A_i \multimap B\). This is, in effect what A&B did in trying to tease out a notion of use of premises. Their notion of a relevant consequence relation is as follows:
Definition 16
(The relevant consequence relation) A relevant deduction of a formula A from a set of formulas \(\varGamma \) in the logic L having only modus ponens, \((\alpha )\), and adjunction, \((\beta )\), as primitive rules, is defined as a Hilbert proof \(A_1, \ldots , A_n\) of A from \(\varGamma \) such that it is possible to mark the \(A_i\)’s with \(\#\)’s according to the following rules:
-
1.
If \(A_i \in \varGamma \), then \(A_i\) is marked.
-
2.
If \(A_i\) is obtained from \(A_j\) and \(A_k\) using modus ponens, then \(A_i\) is marked if either or both of \(A_j\) and \(A_k\) are marked.
-
3.
Adjunction is only used on premises which are either both marked or both unmarked.
-
4.
If \(A_i\) is obtained from \(A_j\) and \(A_k\) using adjunction and both of \(A_j\) and \(A_k\) are marked, then \(A_i\) is marked.
-
5.
No other formulas are marked.
-
6.
As a consequence of (1–5), \(A_n\) is marked.
The existential claim that there is such a proof is written \(\varGamma \vdash ^{r}_\mathbf{L } A\) and expressed as “there exists a relevant derivation of A from \(\varGamma \) in the logic L.”
A&B’s so-called Entailment theorem states that
This property was regarded by A&B as necessary and sufficient for avoiding what they deemed to be relevant fallacies. I showed in Øgaard (2019, thm. 9) that the property also holds for the explosive logic \({\Pi '}_{\!\!\mathbf{E} }\). As there pointed out, however, the property holds for virtually any logic with no more primitive rules than modus ponens and adjunction, and so even classical logic has this property. Having the Entailment theorem, therefore, cannot be regarded as a sufficient property if the variable sharing property is, as A&B thought, a necessary property for avoiding the paradoxes of implication.
The proof of the Entailment theorem in Øgaard (2019) is easily seen to hold for Æ and M. It does not, however, extend to logics with other primitive rules than adjunction and modus ponens for \(\rightarrow \) for the simple reason that such logics are ruled out by definition. Thus relevant consequence is simply not defined for \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\) using A&B’s notion of entailment. It is, however, easy to modify the definition of a relevant deduction so as to cover also these two logics: first of all, the rule-restriction must be lifted so as to allow for \((\gamma )\). Secondly, we update the #-rules so as to include
-
\((\gamma )\) is only used on unmarked premises
-
If \(A_i\) is obtained using \((\gamma )\), then \(A_i\) is unmarked.
This, then, is in effect to limit the application of \((\gamma )\) to logical theorems. Since, however, \((\gamma )\) is admissible in \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{R} ^\mathbf{t} \), an easier option is in fact to simply outlaw any application of \((\gamma )\). Either way, however, using the same type of proof as in Øgaard (2019, thm. 9) it follows that the Entailment theorem also holds for \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and \(\mathbf{R} ^\mathbf{t} [\gamma ]\). All the \(\vdash ^h\)-explosive logics \(\mathbf{E} ^\mathbf{t} [\gamma ], \mathbf{R} ^\mathbf{t} [\gamma ]\), Æ and M, then, satisfy the use-criterion for relevance, namely the Entailment theorem:
Corollary 5
For  ,
,
Øgaard (2019) tentatively suggested that there is nothing more substantial to relevant logics than satisfying the variable sharing property. One of the reasons given for this was that the Entailment theorem as stated by A&B only applies to logics having only modus ponens and adjunction as primitive rules. As it is not evident how it can be modified to cover logics with other rule-sets, demanding that the Entailment theorem should hold, then, seemed to exclude a wide range of logics from consideration too hastily. Note, then, that even if it is upheld as a necessary relevance property, that will not necessarily rule logics with an explosive \(\vdash ^h\)-relation irrelevant, not even logics with modus ponens for the material conditional as a primitive rule.Footnote 26
9 The two consequence relations relations of \(\mathbf{E} ^\mathbf{t} \), \(\mathbf{E} ^\mathbf{t} [\gamma ]\) and Æ
We have seen that \(\rightarrow \) and the enthymematic conditional \(\mapsto \) represent different consequence relations. I mentioned in Sect. 7 that in the case of \(\mathbf{E} ^\mathbf{t} \), modus ponens holds for \(\mapsto \) only enthymematically. This, then, translates to the fact that \(\{A, A\mapsto B\} \nvdash ^r_\mathbf{E ^\mathbf{t} } B\), although \(\{A, A\mapsto B, \mathbf{t} \} \vdash ^r_\mathbf{E ^\mathbf{t} } B\). Thus if \(\mathbf{t} \)—that is the full might of the logical resources entrusted to the logical axioms—might be called upon unrestrictedly, then modus ponens holds for \(\mapsto \). If, as is generally the case with \(\vdash ^r\) for \(\mathbf{E} ^\mathbf{t} , \mathbf{E} ^\mathbf{t} [\gamma ], \mathbf{R} ^\mathbf{t} , \mathbf{R} ^\mathbf{t} [\gamma ]\), Æ and M, however, one can not always conjure up \(\mathbf{t} \) as a logically unrestricted resource, then modus ponens does not hold for \(\mapsto \) seeing as B fails to be relevantly derivable from A and \(A \mapsto B\).
Relevant logics are often motivated as being able to support inconsistent theories non-trivially. Note, then, that it is the presence of these two consequence relations—\(\vdash ^h\) and \(\vdash ^r\)—that allow logics like Æ to non-trivially support inconsistent theories, yet insist that there is something amiss with inconsistency. Such theories can indeed be closed under \(\vdash ^r\), but cannot without trivializing be closed under \(\vdash ^h\). Note, then, that if a set of formulas is closed under \(\vdash ^r\), and contains every logical truth of Æ, then it is also closed under \(\vdash ^h\). Inconsistent \(\vdash ^r\)-theories, then, cannot, according to Æ, be what is called regular theories, that is they cannot contain all the logical theorem—every A such that \(\varnothing \vdash ^h A\). Sometimes it is impertinent to use the Hilbertian consequence relation, as, for instance, when reasoning with counterpossibles;  is, according to Æ, necessarily false, yet it is not the case that any conditional with
is, according to Æ, necessarily false, yet it is not the case that any conditional with  as antecedent is vacuously true. Nor is it the case that any old contradiction entail whatever on just any reading of ‘entails.’ Quite the contrary, in general it is not the case that B is entailed, given the relevant notion of entailment as relevant deducibility, from a contradictory set of premises seeing as it is not always the case that
as antecedent is vacuously true. Nor is it the case that any old contradiction entail whatever on just any reading of ‘entails.’ Quite the contrary, in general it is not the case that B is entailed, given the relevant notion of entailment as relevant deducibility, from a contradictory set of premises seeing as it is not always the case that  . Sometimes, however, one ought to, to paraphrase Achilles (cf. Carroll (1895, p. 280)), let Logic take you by the throat, and force you to accept the conclusion. The forcing does not happen by the might of the premises alone—not always at least—rather it is the premises together with the logical resourses available that conjointly force the conclusion. In this sense it is the case, say Æ, that
. Sometimes, however, one ought to, to paraphrase Achilles (cf. Carroll (1895, p. 280)), let Logic take you by the throat, and force you to accept the conclusion. The forcing does not happen by the might of the premises alone—not always at least—rather it is the premises together with the logical resourses available that conjointly force the conclusion. In this sense it is the case, say Æ, that  , since \(\mathbf{t} \) is to be interpreted as the combined resources of pure logic.
, since \(\mathbf{t} \) is to be interpreted as the combined resources of pure logic.  is also necessarily false, yet any conditional having it as antecedent is vacuously true according to Æ. Æ can, therefore, also differentiate between counterpossibles and between two different notions of consequence.
is also necessarily false, yet any conditional having it as antecedent is vacuously true according to Æ. Æ can, therefore, also differentiate between counterpossibles and between two different notions of consequence.
Note, then, that Æ (and similarly for M) is a quite different logic than its explosive sibling \(\mathbf{E} ^\mathbf{t} [\gamma ]\). The latter logic can non-trivially support inconsistent yet regular theories since it is not the case that  . Using the \(\mathbf{t} /\mathbf{f} \)-enthymematical deduction theorem and the Entailment theorem, however, the only thing that we can infer from such inconsistent theories is that \(\mathbf{f} \vee B\) belongs to it: if both
. Using the \(\mathbf{t} /\mathbf{f} \)-enthymematical deduction theorem and the Entailment theorem, however, the only thing that we can infer from such inconsistent theories is that \(\mathbf{f} \vee B\) belongs to it: if both  and \(\mathbf{t} \) are members of \(\varGamma \) and this set is closed under \(\vdash ^r_\mathbf{E ^\mathbf{t} [\gamma ]}\), then seeing as
and \(\mathbf{t} \) are members of \(\varGamma \) and this set is closed under \(\vdash ^r_\mathbf{E ^\mathbf{t} [\gamma ]}\), then seeing as  if and only if
if and only if  (Thm. 10), using the Entailment theorem yields that
(Thm. 10), using the Entailment theorem yields that  . Since \((\gamma )\) is an admissible rule in \(\mathbf{E} ^\mathbf{t} \), it follows that closing a set of formulas under \(\vdash ^r_\mathbf{E ^\mathbf{t} [\gamma ]}\) yields the same theory as closing under \(\vdash ^r_\mathbf{E ^\mathbf{t} }\). To further explain just how different Æ is with regards to inconsistent regular theories, note that \(A \wedge \mathbf{t} \rightarrow \mathbf{f} \vee B\) is interderivable with
. Since \((\gamma )\) is an admissible rule in \(\mathbf{E} ^\mathbf{t} \), it follows that closing a set of formulas under \(\vdash ^r_\mathbf{E ^\mathbf{t} [\gamma ]}\) yields the same theory as closing under \(\vdash ^r_\mathbf{E ^\mathbf{t} }\). To further explain just how different Æ is with regards to inconsistent regular theories, note that \(A \wedge \mathbf{t} \rightarrow \mathbf{f} \vee B\) is interderivable with  in \(\mathbf{E} ^\mathbf{t} \).Footnote 27 Thus an inconsistent and regular set of formulas will if closed under \(\vdash ^r_\mathbf{E ^\mathbf{t} [\gamma ]}\) or \(\vdash ^r_\mathbf{E ^\mathbf{t} }\) contain the logical falsehood \(\mathbf{f} \), but it can very well be the case that the theory is non-trivial. Lastly, note that this latter fact set \(\mathbf{E} ^\mathbf{t} [\gamma ]\) apart from both Æ- and \(\mathbf{E} ^\mathbf{t} \): for the latter two logics it is the case that any regular relevant theory—a set of formulas containing all the axioms and closed under \(\vdash ^r\)—will also be closed under \(\vdash ^h\). Not so for regular and relevant \(\mathbf{E} ^\mathbf{t} [\gamma ]\)-theories which then need not be closed under its primitive rule \((\gamma )\).
in \(\mathbf{E} ^\mathbf{t} \).Footnote 27 Thus an inconsistent and regular set of formulas will if closed under \(\vdash ^r_\mathbf{E ^\mathbf{t} [\gamma ]}\) or \(\vdash ^r_\mathbf{E ^\mathbf{t} }\) contain the logical falsehood \(\mathbf{f} \), but it can very well be the case that the theory is non-trivial. Lastly, note that this latter fact set \(\mathbf{E} ^\mathbf{t} [\gamma ]\) apart from both Æ- and \(\mathbf{E} ^\mathbf{t} \): for the latter two logics it is the case that any regular relevant theory—a set of formulas containing all the axioms and closed under \(\vdash ^r\)—will also be closed under \(\vdash ^h\). Not so for regular and relevant \(\mathbf{E} ^\mathbf{t} [\gamma ]\)-theories which then need not be closed under its primitive rule \((\gamma )\).
10 Pluralism on the cheap
We have seen how Anderson and Belnap wanted a new theory of entailment, one in which entailment itself was expressible using an object-language conditional. In addition to this, however, they thought that such a theory should be able to express a notion of enthymematic entailment: entailments which are true if only a suppressed true premises is stated explicitly. Whereas the entailment conditional \(\rightarrow \) expresses what A&B thought to be entailment itself, and that the enthymematic conditional only expressed a second-rate version of entailment, both express what can be taken to be consequence relations. At a first glance it seems that A&B only accepted relevant consequence as being a proper consequence relation. The Entailment theorem, however, shows that the relevant consequence relation and the Hilbertian one are interdefinable: even though A&B quite forcefully rejected \(B \rightarrow B\) to be a logical consequence of A, in the sense of not being entailed by A, they quite happily accepted that \(B \rightarrow B\) is enthymematically entailed by A.
A&B write of the Hilbertian notion of consequence in a rather disapproving way—they talk of “Officers” adhering to the “Official” position for which
terms like “deduction,” “from,” “premiss,” “proof,” “hypothesis,” “valid,” “demonstration,” “consequence,” and “argument” have virtually no connection with the same terms as understood outside the Official context—even by the Officer himself, when he takes off his uniform [...]. (Anderson and Belnap 1975, p. 258)
Seeing, however, as this “Official” notion of consequence shows up as a quite valid, although enthymematically so, notion of logical consequence, one should not conclude that A&B sought to completely replace the Hilbertian notion of consequence with their relevant one.Footnote 28 I suggest, rather, that their view is more fruitfully viewed as a pluralistic one: both the relevant and the Hilbert consequence relations apply without restriction, according to A&B, irrespective of subject matter. Adhering to the correctness of both amounts, then, to what Haack (1978, ch. 12) calls global pluralism. Haack ties global pluralism to meaning variance. Hjortland (2013), however, argued that there is one brand of pluralism about logical consequence, namely intra-theoretic pluralism, which is not wedded to meaning variance, at least not to what he calls B-type meaning variance. The basic idea is that B-type meaning variance can occur when different logical systems assign different proof/truth-conditions to a connective and thereby assign different meanings to it. If, however, two consequence relations are definable over the same logical system, then such meaning variance would not occur: “rather than simply the claim that there is more than one admissible consequence relation, intra-theoretic pluralism combines more than one consequence relation in a single logical theory (Hjortland 2013, p. 365). The examples that Hjortland mentions include instances where the same proof system can be used to define more than one consequence relation. This, we have seen, is also the case for the consequence relations \(\vdash ^h\) and \(\vdash ^r\) for logics such as Æ: both are defined over the same proof system, namely over the same set of axioms and rules.Footnote 29 The cases that Hjortland mentions, however, requires commitment to the correctness of at least two ways of defining logical consequence over a proof system seeing as he does not require that the consequence relations be expressible via deduction theorems.Footnote 30 In our case, however, the pluralism is a free lunch as the commitment to both the Hilbertian consequence relation as well as the relevant one can be economized to just one seeing as the one is expressible in the other. Just as A&B incorporate relevant consequence and its enthymematic sibling to account for valid arguments and “merely” enthymematically valid argument, Hjortland states that
Philosophers who think that these systems contain useful consequence relations for modelling different reasoning phenomena can use intra-theoretic pluralism as a way to think about logical theories that combine the consequence relations in a unified theory.
Viewing A&B’s theory of entailment as a pluralistic take on logical consequence yields a more liberal account of their view than their own iconoclastic presentation of it at times seems to allow for. Note, then, that A&B did regard having an enthymematic conditional with a deduction theorem relative to the Hilbertian consequence relation as something “one could hardly get along without” (Anderson and Belnap 1975, p. 259). Should an A&B-inspired relevantist find that \(\vdash ^h\) does not correspond to an admissible notion of logical consequence, then not only will A&B’s sine qua non criterion of having an enthymematic conditional have to be given up, but the theory of entailment has to be altered so as to make no such enthymematic conditional definable. In the case of E this implies giving up not only the Ackermann constant, but also A&B’s favorite way of defining \(\mapsto \) using propositional quantifiers. Even if such be abnegated, however, it seems that \(\vdash ^h\) may quite reasonably be argued to be expressible enthymematically seeing as \(\mathbf{t} \) can in fact be contextually defined so that (simplifying to the one-premise case) \(\{A\} \vdash ^h_\mathbf{E } B\) if and only if \(\varnothing \vdash ^h_\mathbf{E } A \wedge \mathbf{t} ' \rightarrow B\), where \(\mathbf{t} '\) is the long conjunction of every \(p \rightarrow p\) for every propositional variable p occurring in the proof of B from A.Footnote 31
Whatever may be the correct account of A&B’s views of these matters, however, their selection criteria for an adequate theory of entailment seem to commit them to intra-theoretic pluralism about logical consequence. One may try to resist this by sharpening and reevaluating the selection criteria. I suggest, however, that one rather try to enjoy a free lunch.Footnote 32
11 Summary
This paper has provided a systematic account of the selection criteria Anderson and Belnap appealed to in giving what they argued to be a more adequate theory of entailment. These criteria were categorized into three groups: the modal properties, the relevance properties, and the properties pertaining to expressive strength. This paper has shown that A&B’s original relevant logics, E and R, can be extended to become strong and natural explosive logics. There are two ways of doing so: the first is to simply add Ackermann’s \((\gamma )\)-rule—modus ponens for the material conditional, that is disjunctive syllogism—as a primitive rule. This rule is admissible in both E and R, and so the extension is conservative. Anderson and Belnap thought that adding \((\gamma )\) as a primitive rule would destroy the “nice” features of E. However, the modal features of E and quite evidently retained. I’ve also shown that both of the relevance properties—the variable sharing property and the use-criterion formalized as the Entailment theorem—are both retained if \((\gamma )\) is added to either E or R. It was shown, however, that the addition does affect the properties related to expressive strength. Adding \((\gamma )\) results in the failure of the enthymematical deduction theorem for the defined conditional \(A \wedge \mathbf{t} \rightarrow B\), where \(\mathbf{t} \) is the Ackermann constant. It was shown, however, that these logics have a different enthymematic conditional for which a corresponding deduction theorem does hold. However, the expressive criterion of rule normality, that every primitive rule should correspond to a true entailment, fails, seeing as  cannot hold true in any logic which satisfies the variable sharing property seeing as it would yield the explosion axiom
cannot hold true in any logic which satisfies the variable sharing property seeing as it would yield the explosion axiom  .Footnote 33
.Footnote 33
Even though the explosion axiom cannot be a general theorem of a relevant logic, instances of it can be. The other way of extending E and R is to simply add \(\mathbf{t} \wedge \mathbf{f} \rightarrow A\), where  . It was shown that the logics obtained by doing so—called Æ and M—retain all of the properties appealed to by Anderson and Belnap in settling on E and R. Æ and M, unlike E and R, however, have \((\gamma )\) as a derivable rule, and the deduction theorem holds for the material conditional in both logics. The conclusion, then, is that the material conditional cannot be ruled as being “no kind of conditional” using the selection criteria Anderson and Belnap put forth. Not even, to once again use A&B’s phrase, if we bend over backward and uphold not only the legitimacy of the selection criteria, but also what these were thought to select, namely E and R.
. It was shown that the logics obtained by doing so—called Æ and M—retain all of the properties appealed to by Anderson and Belnap in settling on E and R. Æ and M, unlike E and R, however, have \((\gamma )\) as a derivable rule, and the deduction theorem holds for the material conditional in both logics. The conclusion, then, is that the material conditional cannot be ruled as being “no kind of conditional” using the selection criteria Anderson and Belnap put forth. Not even, to once again use A&B’s phrase, if we bend over backward and uphold not only the legitimacy of the selection criteria, but also what these were thought to select, namely E and R.
At last it was suggested that Anderson and Belnap’s take on logical consequence ought to be seen as what Hjortland (2013) calls intra-theoretic pluralism: I’ve argued that Anderson and Belnap in fact end up having to endorse not only the relevant notion of consequence, but also the Hilbertian notion of consequence seeing as the latter is expressible as an enthymematical version of the former.
Notes
For a bit more on the prehistory of relevant logics, see Øgaard (2019, § 2).
Also worth quoting is the colorful remark that “ ‘[m]aterial implication’ is not a ‘kind’ of implication, or so we hold; it is no more a kind of implication than a blunderbuss is a kind of buss” (Anderson and Belnap 1962, p. 21).
Cf. Anderson and Belnap (1975, p. 258).
I should also like to mention a recent novel approach to the implicational paradoxes, namely that argued for by Kerr (2019). Kerr argues that the logic KR—R augmented by
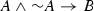 (which, then, also extends CR)—is both superior to classical logic in that it does not validate genuine implicational paradoxes such as \(A \rightarrow (B \rightarrow A)\), and superior to R in that it validates disjunctive syllogism. That relevant logics generally do not validate this rule is identified as the “most unsavoury and counterintuitive aspect of relevant logics” (Kerr 2019, § 5). Kerr appeals to the normativity of logic in classifying
(which, then, also extends CR)—is both superior to classical logic in that it does not validate genuine implicational paradoxes such as \(A \rightarrow (B \rightarrow A)\), and superior to R in that it validates disjunctive syllogism. That relevant logics generally do not validate this rule is identified as the “most unsavoury and counterintuitive aspect of relevant logics” (Kerr 2019, § 5). Kerr appeals to the normativity of logic in classifying 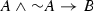 and \(A \rightarrow (B \rightarrow B)\) as merely illusory implicational paradoxes. Kerr’s approach the problem of disjunctive syllogism is highly interesting. Going further into issues connected to the normativity of logic, or Kerr’s distinction between genuine and illusory implicational paradoxes is regrettably beyond the scope of this paper.
and \(A \rightarrow (B \rightarrow B)\) as merely illusory implicational paradoxes. Kerr’s approach the problem of disjunctive syllogism is highly interesting. Going further into issues connected to the normativity of logic, or Kerr’s distinction between genuine and illusory implicational paradoxes is regrettably beyond the scope of this paper.Note also that both (Ax13) and (Ax14) become derivable upon adding the two \(\mathbf{t} \)-axioms, and so \(\mathbf{E} ^\mathbf{t }\) may be taken as simply (Ax1)–(Ax12), \((\mathbf{t} 1)\)–\((\mathbf{t} 2)\) together with the rules \((\alpha )\) and \((\beta )\).
See Øgaard (2019, § 4.1) for details.
I hasten to emphasize that the language is not infinitary and so \(\bigwedge \{A \mathbin {|} \varGamma \vdash ^h A\}\) is not a well-formed formula.
This result goes back to Ackermann (1956, p. 125).
All displayed models in this paper have been generated by John Slaney’s computer program MaGIC (Slaney 1995). Such models will be depicted with a displayed ordering and matrices for at least \(\rightarrow \) and
 . Conjunction and disjunction are to be interpreted as infimum and supremum over the displayed ordering. Rules are regarded to hold in the model if they preserve designated values—the members of the set \({\mathcal {T}}\)—if the premises are all evaluated to designated values, then the conclusion is also evaluated to some designated value. I will also list how to interpret the truth-constants as well as any formula needed to make the model a counter-model for the requisite formula/rule.
. Conjunction and disjunction are to be interpreted as infimum and supremum over the displayed ordering. Rules are regarded to hold in the model if they preserve designated values—the members of the set \({\mathcal {T}}\)—if the premises are all evaluated to designated values, then the conclusion is also evaluated to some designated value. I will also list how to interpret the truth-constants as well as any formula needed to make the model a counter-model for the requisite formula/rule.Note that also A&B read \(\Box A\) not only as A being necessarily true, but also as being entailed by logic. With regards to the formula \(\Box A \rightarrow \Box \Box A\), for instance, they explicitely allow the reading “if A follows from a law of logic, then that fact itself follows from a law of logic” (Anderson and Belnap 1975, p. 118).
See Øgaard (1975, § 5.2, §§ 22.1.1–2) for details.
The same model is also presented (in much more accessible way) in Anderson et al (1992, § 45). It is also easy to verify that \(\mathbf{t} \wedge \mathbf{f} \rightarrow A\) also holds in the 10-element model used by Maksimova to strengthen Ackermann’s result (cf. Anderson and Belnap 1975, § 22.1.1). The logic \({\Pi '}_{\!\!\mathbf{E} }\) of Øgaard (2019) added the axiom
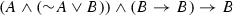 to a weakened version of E and showed that it satisfies many of E-properties treasured by A&B. No mention, however, was made of the Ackermann property. Note, then, that Ackermann’s model, although not Maksimova’s, also satisfies
to a weakened version of E and showed that it satisfies many of E-properties treasured by A&B. No mention, however, was made of the Ackermann property. Note, then, that Ackermann’s model, although not Maksimova’s, also satisfies 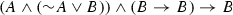 and is therefore a model for \({\Pi '}_{\!\!\mathbf{E} }\) as well.
and is therefore a model for \({\Pi '}_{\!\!\mathbf{E} }\) as well.As will be evident, one could get Æ(Æ5) to extend and not just interpret S4(S5) by simply formulating Æ(Æ5) with a primitive \(\Box \) and then add \(\Box A \leftrightarrow ((A \rightarrow A) \rightarrow A)\) as a separate axiom.
There are further reasons for insisting on the direct translation. For non-direct translations, what is expressed is then a logical concept as this is expressed in another logic. That one logic can express a logical concept according to some other logic can be an interesting feature, but in general it is the logical concept according to the correct logic—modality according to the theory of entailment in the case of \(\mathbf{E} ^\mathbf{t} \)—which is the concept that we want to give a theory of. At least A&B thought that S4 gave an incorrect account of entailment, but a correct account of modality where it only to be expressed using E’s notion of entailment and not the strict implication of S4 (cf. Anderson and Belnap 1975, §§ 2&11). Meyer (1970) showed that E interprets S4 on two different translations. For our purposes, let’s focus on Meyer’s result pertaining to \(\mathbf{E} ^\mathbf{t} \). Meyer uses the fact that S4 can be axiomatized as \(\mathbf{E} ^\mathbf{t} \) strengthened by \(A \rightarrow (B \rightarrow B)\), where \(\rightarrow \) is then the strict implication more commonly designated by the fish-hook
 and S4’s
and S4’s 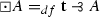 . The translations translate
. The translations translate  , \(\wedge \) and \(\vee \) homophonically, while one uses Ackermann’s translation
, \(\wedge \) and \(\vee \) homophonically, while one uses Ackermann’s translation 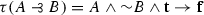 , whereas the other uses Meyer’s weak enthymematic translation
, whereas the other uses Meyer’s weak enthymematic translation 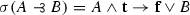 . As shown in the appendix,
. As shown in the appendix, 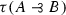 and
and 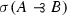 are interderivable in \(\mathbf{E} ^\mathbf{t} \), although they are not equivalent and so \(\tau \) and \(\sigma \) amount to different translations. Ackermann (1958) used \(\tau \) to show that \({\Pi '}\) (extended with a truth constant corresponding to \(\mathbf{f} \)) interprets at least all of Lewis’ logic S2. Meyer’s proofs, then, shows that it interprets all of S4 in the sense that \(\vdash ^h_\mathbf{S4 } A\) if and only if \(\vdash ^h_\mathbf{E ^\mathbf{t} } \tau (A)\) if and only if \(\vdash ^h_\mathbf{E ^\mathbf{t} } \sigma (A)\). To see that being necessarily true in the \(\boxdot \)-sense of this, and being entailed by logic are not equivalent notion, note that \(\tau \!\boxdot p\) and \(\sigma \!\boxdot p\) are equivalent, but that \(\tau \!\boxdot p \rightarrow (\mathbf{t} \rightarrow p)\) is not a logical truth of \(\mathbf{E} ^\mathbf{t} \). As a further example of how different being \(\mathbf{S4} \)-necessarily true under \(\sigma \) and \(\tau \) are different from that of \(\Box \), note that neither \(\tau \!\boxdot p \rightarrow p\), nor \(\tau \!\boxdot (p \rightarrow q) \rightarrow (\tau \!\boxdot p \rightarrow \tau \!\boxdot q)\) are logical truths of \(\mathbf{E} ^\mathbf{t} \) either (MaGIC easily provides a counter-models; I leave it as exercises for the reader). I would like to thank one of the referees for pressing this issue. Both Ackermann’s \(\tau \) and Meyer’s \(\sigma \) are interesting as it turns out (see the appendix for proofs) that
are interderivable in \(\mathbf{E} ^\mathbf{t} \), although they are not equivalent and so \(\tau \) and \(\sigma \) amount to different translations. Ackermann (1958) used \(\tau \) to show that \({\Pi '}\) (extended with a truth constant corresponding to \(\mathbf{f} \)) interprets at least all of Lewis’ logic S2. Meyer’s proofs, then, shows that it interprets all of S4 in the sense that \(\vdash ^h_\mathbf{S4 } A\) if and only if \(\vdash ^h_\mathbf{E ^\mathbf{t} } \tau (A)\) if and only if \(\vdash ^h_\mathbf{E ^\mathbf{t} } \sigma (A)\). To see that being necessarily true in the \(\boxdot \)-sense of this, and being entailed by logic are not equivalent notion, note that \(\tau \!\boxdot p\) and \(\sigma \!\boxdot p\) are equivalent, but that \(\tau \!\boxdot p \rightarrow (\mathbf{t} \rightarrow p)\) is not a logical truth of \(\mathbf{E} ^\mathbf{t} \). As a further example of how different being \(\mathbf{S4} \)-necessarily true under \(\sigma \) and \(\tau \) are different from that of \(\Box \), note that neither \(\tau \!\boxdot p \rightarrow p\), nor \(\tau \!\boxdot (p \rightarrow q) \rightarrow (\tau \!\boxdot p \rightarrow \tau \!\boxdot q)\) are logical truths of \(\mathbf{E} ^\mathbf{t} \) either (MaGIC easily provides a counter-models; I leave it as exercises for the reader). I would like to thank one of the referees for pressing this issue. Both Ackermann’s \(\tau \) and Meyer’s \(\sigma \) are interesting as it turns out (see the appendix for proofs) that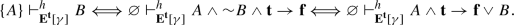
That reasoning by cases holds for Æ (and M) follows easily from the enthymematical deduction theorem to be proven in Sect. 7.
See Øgaard (2019, thm. 3) for more details).
Yang describes \(\mathbf{t} \) as the conjunction of every truth. This is appropriate for \(\mathbf{R} ^\mathbf{t }\) since \(A \leftrightarrow (\mathbf{t} \rightarrow A)\) is a theorem for it. As is made plain here, nothing hangs on assigning \(\mathbf{t} \) this interpretation rather than the weaker one given here.
\({\Pi '}\) is sometimes presented as having the rule \(A \rightarrow (B \rightarrow C), B \Vdash A \rightarrow C\) as a primitive rule. This rule, called \((\delta )\) by Ackermann, was restricted to instances where B is a logical theorem. \((\delta )\) thus restricted holds also in E. See Øgaard (2019, § 3) for details. To avoid confusion, however, I will stick to ‘\(\mathbf{E} [\gamma ]\).’
In fact S4\(^+\) is theorem-wise identical to the positive fragment of E augmented by \(A \rightarrow (B \rightarrow B)\).
A&B uses the term “Official deduction theorem” for a deduction theorem such as the enthymematical one, although they state it as merely the left-to-right half of what I have done.
Which is a modified version of Belnap’s Doctoral Dissertation.
See Lance (1988) for a discussion of the idea of R’s \(\rightarrow \) expressing a notion of contingent relevant implication.
A&B’s notion of a relevant consequence was generalized in Brady (1993, thm. 3) to cover relevant logics contained in T and extending the weak logic B augmented by the axiom \(A \wedge (A \rightarrow B) \rightarrow B\). Still, this does not cover the important class of contractionless relevant logics. However, I’ve recently managed to generalize the theorem to cover any extension of B (and even weaker logics still). Details are in Øgaard (2021). Thus upholding the Entailment theorem as a necessary criterion of relevance excludes few, if any, logics of interest.
See the appendix for a proof.
Or if they did, one should conclude that they shouldn’t have.
On the semantical side, Hjortland (2013, fn. 13) mentions global vs. logic semantic consequence in Kripke semantics. Note, then, that the model-theoretic equivalent of \(\vdash ^h\) and \(\vdash ^r\) are in the case of logics such as \(\mathbf{E} ^\mathbf{t} \) truth-preservance over the “normal” states—those which validate every logical axiom—whereas the semantic equivalent of \(\vdash ^r\) is truth-preservance over every state. The semantic equivalent of \(\vdash ^h\) for \(\mathbf{E} ^\mathbf{t} [\gamma ]\), however, is truth-preservance over the “base” world seeing as other “normal” states need not treat \((\gamma )\) as a truth-preserving rule. For the semantics of \(\mathbf{E} ^\mathbf{t} \) and \(\mathbf{E} ^\mathbf{t} [\gamma ]\), see Routley et al. (1982, appendix 1).
One of the examples Hjortland mentions is the case where the consequence relations of the three-valued logics K3 and LP are defined using the same three-sided sequent system. Neither of these logics have a conditional for which a deduction theorem holds—K3 has in fact no logical theorems, whereas Beall et al. (2013) showed that LP has no non-trivial way of defining a conditional for which modus ponens holds.
This easily follows by studying the proof of the the enthymematical deduction theorem and applying the results from Anderson and Belnap (1959).
I should note that this kind of pluralism has already been suggested for other relevant logics. Mares and Paoli (2014) argue for a version of intra-theoretic pluralism applied to what is known as the internal and external consequence relation of certain relevant logics. On this form of pluralism, see also Dicher (2020).
This, of course, assumes that \(\rightarrow \) is provably transitive. There are non-transitive approaches to relevant logics, although going further into this is beyond the scope of this paper.
References
Ackermann, W. (1956). Begründung einer strengen Implikation. Journal of Symbolic Logic, 21(2), 113–128. https://doi.org/10.2307/2268750.
Ackermann, W. (1958). Über die Beziehung zwischen strikter und strenger Implikation. Dialectica, 12(3/4), 213–222. https://doi.org/10.1111/j.1746-8361.1958.tb01459.x.
Anderson, A. R., & Belnap, N. D. (1959). Modalities in Ackermann’s “rigorous implication”. Journal of Symbolic Logic, 24(2), 107–111. https://doi.org/10.2307/2964754.
Anderson, A. R., & Belnap, N. D. (1961). Enthymemes. The Journal of Philosophy, 58(23), 713–723. https://doi.org/10.2307/2023169.
Anderson, A. R., & Belnap, N. D. (1962). The pure calculus of entailment. Journal of Symbolic Logic, 27(1), 19–52. https://doi.org/10.2307/2963676.
Anderson, A. R., & Belnap, N. D. (1975). Entailment: The logic of relevance and necessity (Vol. 1). Princeton: Princeton University Press.
Anderson, A. R., Belnap, N. D., & Dunn, M. J. (1992). Entailment: The logic of relevance and necessity (Vol. 2). Princeton: Princeton University Press.
Beall, J., Forster, T., & Seligman, J. (2013). A note on freedom from detachment in the logic of paradox. Notre Dame J. Formal Logic, 54(1), 15–20. https://doi.org/10.1007/978-94-009-8356-4_13.
Beall, J., & Restall, G. (2005). Logical pluralism. Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199288403.001.0001.
Belnap, N. D. (1960a). Entailment and relevance. Journal of Symbolic Logic, 25(2), 144–146. https://doi.org/10.2307/2964210.
Belnap, N. D. (1960b). A formal analysis of entailment. New Haven: Technical report.
Bimbó, K., & Dunn, J. M. (2018). Larisa Maksimova’s early contributions to relevance logic. In Odintsov, S., (ed), Larisa Maksimova on implication, interpolation, and definability (pp. 33–60). Cham: Springer. https://doi.org/10.1007/978-3-319-69917-2_3.
Brady, R. T. (1993). Rules in relevant logic-II: Formula representation. Studia Logica, 52(4), 565–585. https://doi.org/10.1007/BF01053260.
Carroll, L. (1895). What the tortoise said to Achilles. Mind, 4(14), 278–280. https://doi.org/10.1093/mind/IV.14.278.
Dicher, B. (2020). Variations on intra-theoretical logical pluralism: Internal versus external consequence. Philosophical Studies, 177(3), 667–686. https://doi.org/10.1007/s11098-018-1199-z.
Dunn, J. M. & Restall, G. (2002). Relevance logic. In Gabbay, D. M. and Guenthner, F., (eds.), Handbook of Philosophical Logic, (Vol. 6, pp. 1–128). Dordrecht: Springer. https://doi.org/10.1007/978-94-017-0460-1_1.
Galatos, N., Jipsen, P., Kowalski, T., & Ono, H. (2007). Residuated lattices: An algebraic glimpse at substructural logics. Amsterdam: Elsevier. https://doi.org/10.1016/S0049-237X(07)80005-X.
Giambrone, S., & Meyer, R. K. (1989). Completeness and conservative extension results for some Boolean relevant logics. Studia Logica, 48(1), 1–14. https://doi.org/10.1007/BF00370629.
Haack, S. (1978). Philosophy of logics. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511812866.
Hjortland, O. T. (2013). Logical pluralism, meaning-variance, and verbal disputes. Australasian Journal of Philosophy, 91(2), 355–373. https://doi.org/10.1080/00048402.2011.648945.
Hughes, G., & Cresswell, M. (1996). A new introduction to modal logic. London: Routledge. https://doi.org/10.4324/9780203028100.
Humberstone, L. (2010). Smiley’s distinction between rules of inference and rules of proof. In J. Lear & A. Oliver (Eds.), The force of argument: Essays in honor of timothy smiley (pp. 107–126). New York: Routledge. https://doi.org/10.4324/9780203859810.
Kerr, A. D. (2019). A plea for KR. Synthese,. https://doi.org/10.1007/s11229-019-02265-y.
Lance, M. (1988). On the logic of contingent relevant implication: a conceptual incoherence in the intuitive interpretation of R. Notre Dame Journal of Formal Logic, 29(4), 520–529. https://doi.org/10.1305/ndjfl/1093638016.
Maksimova, L. L. (1966). Formal’nye vyvody v ischislenii strogoǐ implikatsii. Algebra i Logika, 5(6), 33–39.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43(2), 439–469. https://doi.org/10.1007/s10992-013-9268-4.
Mares, E., & Standefer, S. (2017). The relevant logic E and some close neighbours: A reinterpretation. IfCoLog Journal of Logics and Their Applications, 4(3), 695–730.
Mares, E. D. (1992). The semantic completeness of RK. Reports on Mathematical Logic, 26, 3–10.
Mares, E. D. (1993). Classically complete modal relevant logics. Mathematical Logic Quarterly, 39(1), 165–177. https://doi.org/10.1002/malq.19930390119.
Mares, E. D. (2000). CE is not a conservative extension of E. Journal of Philosophical Logic, 29(3), 263–275. https://doi.org/10.1023/A:1004731401855.
Mares, E. D., & Meyer, R. K. (1992). The admissibility of \(\gamma \) in R4. Notre Dame J. Formal Logic, 33(2), 197–206. https://doi.org/10.1305/ndjfl/1093636096.
Mares, E. D., & Meyer, R. K. (1993). The semantics of R4. Journal of Philosophical Logic, 22(1), 95–110. https://doi.org/10.1007/BF01049182.
Meyer, R. K. (1970). E and S4. Notre Dame J. Formal Logic, 11(2), 181–199. https://doi.org/10.1305/ndjfl/1093893935.
Meyer, R. K. (1974). New axiomatics for relevant logics. I. Journal of Philosophical Logic, 3(1), 53–86. https://doi.org/10.1007/BF00652071.
Meyer, R. K., & Dunn, J. M. (1969). E, R and \(\gamma \). Journal of Symbolic Logic, 34, 460–474. https://doi.org/10.2307/2270909.
Meyer, R. K., & Routley, R. (1974). Classical relevant logics II. Studia Logica, 33(2), 183–194. https://doi.org/10.1007/BF02120493
Meyer, R. K., & Routley, R. (1974). Classical relevant logics. II. Studia Logica, 33(2), 183–194. https://doi.org/10.1007/BF02120493.
Øgaard, T. F. (2017). Skolem functions in non-classical logics. Australasian Journal of Logic, 14(1), 181–225.
Øgaard, T. F. (2019). Non-Boolean classical relevant logics I. Synthese. https://doi.org/10.1007/s11229-019-02507-z.
Øgaard, T. F. (2020a). Boolean negation and non-conservativity I: Relevant modal logics. Logic Journal of the IGPL,. https://doi.org/10.1093/jigpal/jzaa019.
Øgaard, T. F. (2020b). Boolean negation and non-conservativity III: The Ackermann constant. Logic Journal of the IGPL. https://doi.org/10.1093/jigpal/jzaa021.
Øgaard, T. F. (2021). Entailment generalized. Under review.
Read, S. (1988). Relevant logic: A philosophical examination of inference. Oxford: Basil Blackwell.
Restall, G. (1999). Negation in relevant logics (how I stopped worrying and learned to love the Routley star). In D. M. Gabbay & H. Wansing (Eds.), What is Negation? (pp. 53–76). Berlin: Springer. https://doi.org/10.1007/978-94-015-9309-0_3.
Routley, R., & Meyer, R. K. (1972). The semantics of entailment-II. Journal of Philosophical Logic, 1(1), 53–73. https://doi.org/10.1007/BF00649991
Routley, R., Meyer, R. K., Plumwood, V., & Brady, R. T. (1982). Relevant logics and their rivals (Vol. 1). Atascadero: Ridgeview.
Slaney, J. K. (1995). MaGIC, Matrix Generator for Implication Connectives: Release 2.1 notes and guide. Technical report. Retrieved November 12, 2010 from http://ftp.rsise.anu.edu.au/techreports/1995/TR-ARP-11-95.dvi.gz.
Yang, E. (2013). R and relevance principle revisited. Journal of Philosophical Logic, 42(5), 767–782. https://doi.org/10.1007/s10992-012-9247-1.
Acknowledgements
I am very grateful to the participants of the Bergen Logic Group and the audience of the LanCog Workshop on Substructural Logics for constructive feedback. Special thanks go to Ole Thomassen Hjortland and the anonymous referees for their comments and suggestions which helped improve this paper considerably.
Funding
Open access funding provided by University of Bergen (incl Haukeland University Hospital).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The quote is from ch. 173 of Neckam’s De Naturis Rerum, here requoted from Read (1988, p. 31).
Appendix: Enthymematic conditionals and deduction theorems
Appendix: Enthymematic conditionals and deduction theorems
This appendix regards the three enthymematic conditionals \(\mapsto , \hookrightarrow \) and \(\rightarrowtail \), where

and the deduction theorems they support.
Theorem 8
(\(\mathbf{t} \)-enthymematic deduction theorem) Let L be any axiomatic extension of \(\mathbf{E} ^\mathbf{t} \) for which the rule \(C \vdash ^h \mathbf{t} \rightarrow C\) is at least admissible, then
Proof
The right to left direction is trivial since modus ponens holds for \(\rightarrow \) and \(\mathbf{t} \) is a theorem. The other direction is an induction on the length of proof. To make the presentation a bit friendlier, let A be the formula \(\bigwedge _{i\le n}A_i \wedge \mathbf{t} \).
Assume that \(B_1, \ldots , B_n\) is the Hilbert proof of B from \(\{A_1, \ldots , A_n\}\). Then if \(B_j\) is one of the \(A_i\)’s, \(A \rightarrow B_j\) is obviously a logical theorem. If \(B_j\) is an axiom, then since \(\{C\} \vdash ^h \mathbf{t} \rightarrow C\) is admissible, we get that \(\mathbf{t} \rightarrow B_j\) is a theorem, and therefore that \(A \rightarrow B_j\) is too.
Now assume that \(B_j\) is obtained from some \(B_k\) and \(B_l\) using adjunction (the \(\beta \)-rule). We may then assume for inductive hypothesis that both \(A \rightarrow B_k\) and \(A \rightarrow B_l\) are theorems. Since \((A \rightarrow B_k) \wedge (A \rightarrow B_l) \rightarrow (A \rightarrow B_k \wedge B_l)\) is an instance of (Ax5), we then get that \(A \rightarrow B_k \wedge B_l\) is a theorem.
Assume lastly that \(B_j\) is obtained from some \(B_k\) and \(B_l\) using modus ponens (the \(\alpha \)-rule), and let \(B_l\) therefore be the formula \(B_k \rightarrow B_j\). From the inductive hypothesis that both \(A \rightarrow B_k\) and \(A \rightarrow (B_k \rightarrow B_j)\) are theorems, one gets \(A \rightarrow (B_k \wedge (B_k \rightarrow B_j))\) using (Ax5). Since \(B_k \wedge (B_k \rightarrow B_j) \rightarrow B_j\) is a logical theorem, we then get \(A \rightarrow B_j\) which then ends the proof. \(\square \)
Theorem 10
(\(\mathbf{t} /\mathbf{f} \)-enthymematic deduction theorem) Let L be any axiomatic extension of \(\mathbf{E} ^\mathbf{t} [\gamma ]\) for which the rule \(\{C\} \vdash ^h \mathbf{t} \rightarrow C\) is at least admissible, then
Proof
The right to left direction is as the above proof, only with an added application of \((\gamma )\) in order to derive B from \(\mathbf{f} \vee B\) and \(\mathbf{t} \).
The left to right direction is in the base case also similar to the proof above. That leaves only the three primitive rules. Again we let A be the formula \(\bigwedge _{i\le n}A_i \wedge \mathbf{t} \).
In the case of adjunction the inductive hypothesis yields that both \(A \rightarrow \mathbf{f} \vee B_k\) and \(A \rightarrow \mathbf{f} \vee B_l\) are logical theorems. Using (Ax5) we then obtain that \(A \rightarrow (\mathbf{f} \vee B_k) \wedge (\mathbf{f} \vee B_l)\). \((\mathbf{f} \vee B_k) \wedge (\mathbf{f} \vee B_l) \rightarrow \mathbf{f} \vee (B_k \wedge B_l)\) is a logical theorem (use the distribution axiom (Ax4)), and so \(A \rightarrow \mathbf{f} \vee (B_k \wedge B_l)\) follows by transitivity.
In the case of modus ponens the inductive hypothesis yields that both \(A \rightarrow \mathbf{f} \vee B_k\) and \(A \rightarrow \mathbf{f} \vee (B_k \rightarrow B_j)\) are theorems, and so, as in the adjunction-case, we get that \(A \rightarrow \mathbf{f} \vee (B_k \wedge (B_k \rightarrow B_j)) \) is a theorem as well. \(B_k \wedge (B_k \rightarrow B_j) \rightarrow B_j\) is a logical theorem (use the contraction axiom (Ax7)), and so simple fiddling yields that so is \(\mathbf{f} \vee (B_k \wedge (B_k \rightarrow B_j)) \rightarrow \mathbf{f} \vee B_j\). Transitivity of \(\rightarrow \), then, yields \(A \rightarrow \mathbf{f} \vee B_j\).
In the case of \((\gamma )\) the inductive hypothesis yields that both \(A \rightarrow \mathbf{f} \vee B_k\) and  are theorems. Using Lemma 3 below, then, yields \(A \rightarrow \mathbf{f} \vee B_j\) which ends the proof. \(\square \)
are theorems. Using Lemma 3 below, then, yields \(A \rightarrow \mathbf{f} \vee B_j\) which ends the proof. \(\square \)
Lemma 3

Proof

\(\square \)
Lemma 4

Proof
(1)

(2)

\(\square \)
Corollary 6
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Øgaard, T.F. Non-Boolean classical relevant logics II: Classicality through truth-constants. Synthese 199, 6169–6201 (2021). https://doi.org/10.1007/s11229-021-03065-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-021-03065-z






 :
:

 by
by
 (which, then, also extends CR)—is both superior to classical logic in that it does not validate genuine implicational paradoxes such as
(which, then, also extends CR)—is both superior to classical logic in that it does not validate genuine implicational paradoxes such as 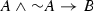 and
and  . Conjunction and disjunction are to be interpreted as infimum and supremum over the displayed ordering. Rules are regarded to hold in the model if they preserve designated values—the members of the set
. Conjunction and disjunction are to be interpreted as infimum and supremum over the displayed ordering. Rules are regarded to hold in the model if they preserve designated values—the members of the set 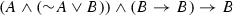 to a weakened version of E and showed that it satisfies many of E-properties treasured by A&B. No mention, however, was made of the Ackermann property. Note, then, that Ackermann’s model, although not Maksimova’s, also satisfies
to a weakened version of E and showed that it satisfies many of E-properties treasured by A&B. No mention, however, was made of the Ackermann property. Note, then, that Ackermann’s model, although not Maksimova’s, also satisfies 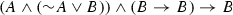 and is therefore a model for
and is therefore a model for  and S4’s
and S4’s 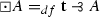 . The translations translate
. The translations translate  ,
, 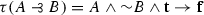 , whereas the other uses Meyer’s weak enthymematic translation
, whereas the other uses Meyer’s weak enthymematic translation 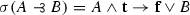 . As shown in the appendix,
. As shown in the appendix, 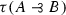 and
and 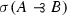 are interderivable in
are interderivable in