1 Introduction

Compositionality is exhibited when a full statement in a language is comprised of component parts that contribute to its meaning. E.g. “the apple is red" and “the traffic light is red" are two distinct statements that have “red" as a component term. There are a number of ways of precisifying informal notions of compositionality. It is thought to be a key feature of human language, differentiating it from other animal communication (Hauser et al., 2002; Scott-Phillips & Blythe, 2013). Lewis initially developed signaling games as a way of showing how communicative conventions can arise without prior knowledge of a language (Lewis, 1969). Later, Skyrms showed how Lewis signaling games can be understood as evolutionary games accessible to agents with low-rationality learning dynamics (Skyrms, 2008, 2010). Recently, Sterelny and Planar have advocated the use of Lewis-Skyrms signaling games for modeling the early evolution of human language (Planer & Sterelny, 2021). There are some signaling game models that have been invoked in explanations of how and why humans acquired compositional language (Franke, 2015; Steinert-Threlkeld, 2016a). However, the signaling game literature has yet to provide concrete models that exhibit important baseline types of compositionality, e.g. what Sterelney and Planar call linear syntax. This paper shows how such compositionality can obtain.

The pyow-hack signaling game model exhibits meaningful compositions sensitive to the ordering of terms. However, some of the game’s structural features have not yet been explicated in the established literature. Consequently, the paper begins with describing two simpler signaling games along with some basic terms and diagrams for describing signaling games. Section 2.1 presents a trivially compositional game, which was initially developed by Barrett (2007) to describe the evolution of kind language. Next, Sect. 2.2 outlines the progression of three properties of signaling games that will be combined to produce ordered compositions in the pyow-hack game: sender-compositionality, receiver-compositionality, and sender independent terms. It also shows that the model from Sect. 2.1 already meets the definition of sender-compositionality. Section 2.3 further explicates receiver-compositionality using a hierarchical signaling game model, which was originally developed in a pair of papers by Barrett et al. (2019), Barrett et al. (2018). Then, Sect. 3.1 outlines the behavior of putty-nosed monkeys, which have an alarm call system with linear syntax, and then 3.2 presents the pyow-hack game, in which a signaling system analogous to the monkey’s can obtain. Lastly, Sect. 4 reviews the three properties of the pyow-hack game which allow for ordered compositions to obtain.

2 Ancient Artisans: Compositionality in Prior Signaling Game Models

This section precisifies three types of compositionality in order of increasing complexity. Simultaneously, it introduces diagrams of the signaling game models. These diagrams represent both the structure of a game and the reinforced dispositions of its players. Understanding how game structure relates to reinforcement of dispositions is essential to understanding compositionality in signaling games. This is not immediately apparent Sect. 2.1’s trivially compositional game. However, Sect. 2.2, on sender-compositionality and its extensions, shows how one can erroneously consider distinct terms as identical when attending to only game structure. Finally, Sect. 2.3 explicates receiver-compositionality with direct reference to the reinforcement of dispositions.

This paper illustrates the signaling game models with a fictional story of prehistoric artisans, Devasena, Valli, and Narundi. Devasena is a logistics expert. She knows whether there is a better supply of wood or clay; when Devasena wears blue (b_) there is a better supply of wood, and when she wears red (r_) there is a better supply of clay. Valli is a market strategist. She knows whether pots or figurines are in greater demand; when Valli wears blue (_b) pots are in demand, and when she wears red (_r) figurines are in demand. Narundi manages acquisitions. She observes what colors Devasena and Valli are wearing and brings either wood or clay along with either tools for making pots or tools for making figurines. Thus when rb (Devasena wears red and Valli blue), Narundi brings clay and tools for making pots. Since the two term statements in this signaling system are merely conjunctive (i.e. the intersection of two properties), it is called trivially compositional (Steinert-Threlkeld, 2020). There are no overbearing reasons for considering rb as a single statement with two component parts rather than understanding it as two independent statements, one made by Devasena and the other by Valli.

2.1 Learning Trivial Compositionality

The ancient artisans story is called a two-term two-sender one-receiver game in the established literature (Barrett, 2007, 2018, 2019). In this game there are four states of nature (needing wood pot, wood figurine, clay pot, or clay figurine supplies), four correspondingly appropriate actions (bringing the corresponding supplies), and two terms (b and r). How could Devasena, Valli, and Narundi acquire their signaling system without any established communicative conventions, without knowing whether Devasena or Valli is more attune to market demand or material supplies? The prior literature has shown that such signaling systems can arise through basic Roth-Erev reinforcement learning.

The reinforcement procedure is as follows. Suppose that Devasena and Valli each have four urns associating one and only one with the four states of nature: supply and demand for wood pots, wood figurines, clay pots, and clay figurines. In each urn, they place one red stone and one blue stone. Narundi has four urns associating each with one of the four signals she can receive: bb, br, rb, and rr. Narundi places four tokens in each of her urns corresponding to the four actions she can perform: bring wood pot, wood figurine, clay pot, or clay figurine supplies. Each day Devasena and Valli observe the state of nature and then draw a stone at random with equal probability from their corresponding urns to determine what color to wear. Narundi then observes Devasena and Valli’s colors and likewise draws randomly from her corresponding urn to determine what action to perform. If the action matches the state of nature, the day is a success. Consequently, each player returns what was drawn to the urn from which it was drawn along with an additional stone or token of the same type; thus, it is more likely that, when the same state of nature occurs in the future, the same signals and then action will occur. If Narundi’s action does not match the state of nature, then the day is a failure. Consequently, stones and tokens are returned to the urns that they were drawn from leaving the probabilities of signals and actions unchanged.

Fig. 1
figure 1

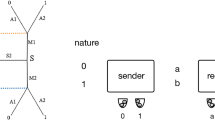
A Signaling System for the two-term two-sender one-receiver signaling game. To indicate the quantities of different types of stones, each urn is depicted with multiple boxes, one box for each type of stone/token in the urn. The most likely stones/tokens to be drawn from a urn are indicated the darker shaded in boxes

Full size image

The entirety of what occurs on a single day is called a single play of the game. A set of n repeated plays is called an n-run. The only way to know the outcome of a run is to actually perform all of the plays in a run. A strategy profile describes a sender or receiver’s dispositions for all states of nature or signals that she can observe. Figure 1 shows both the structure of the game and a set of strategy profiles that could, in principle, be reached through the reinforcement procedure just described. When a set of strategy profiles describes dispositions such that for a state of nature the correct action is performed, it is called a signaling system. The set of strategy profiles in Fig. 1 describe a signaling system in this sense. A run is successful if it converges to a signaling system. An easy and close approximate measure of a run’s success is commonly performed by checking whether the run’s cumulative success rate is above an appropriate cutoff. The cumulative success rate is defined as \(\frac{\# \text { of successful plays}}{\# \text { of plays}}\). In the ancient artisans game there are four equally probable states of nature with unique corresponding actions. So if a strategy profile tends to lead to successful plays for all but one of the states of nature, we should expect a run with that strategy profile to have a cumulative success rate near 0.75. Runs that tend to have successful plays for all states of nature have a cumulative success rate that converges towards 1. Consequently, in the ancient artisans game, it is reasonable to use a cutoff of 0.8 and measure only those runs that have a cumulative success rate greater than 0.8 as successful. Using this measure, after \(10^6\) plays per run under simple reinforcement learning, the run success rate in the ancient artisans game is approximately 73% (Barrett, 2007).

This game’s dynamics are best described as involving two distinct senders, each with her own strategy profile. However, distinct senders in a signaling game model need not represent distinct organisms in the world. The reinforcement dynamics of drawing stones from an urn is intended to represent an organism’s internal mechanisms for learning through reinforcement conditioning. Consequently, one might think of different senders in a game as representing different functional components of a single organism. In the ancient architects game, this might look like a single person using Devasena’s draws to determine whether to wear a blue or a red top while using Valli’s draws to determine whether to wear blue or red pants. Section 2.3 adds an executive send to the game that could perhaps be thought of as modeling a person’s prefrontal cortex determining whether to attend to their Devasena dispositions, Valli dispositions, or both. Later, in modeling monkeys, different basic senders might represent different functional components responsible for the first or second term in an alarm call sequence.Footnote 1 Though it should also be noted that the game in Sect. 3 succeeds in producing a type of compositionality novel to signaling games irrespective of whether or not it accurately reflects how the monkeys acquired their alarm calls.

2.2 Sender-Compositionality and Its Extensions

The definition of trivial compositionality has mostly been used in critique. It does not define a type of compositionality that can easily be extended to yield a more sophisticated type of compositionality. Sender-compositionality is a type of compositionality that is useful for building up more sophisticated types of compositionality; it is also exhibited in the ancient artisans story. Call a set of strategy profiles in a signaling game sender-compositional if there is a term that is transmitted as a component of at least two distinct statements. E.g. Devasena wearing red (r_) is a component of statements rb and rr.

Franke (2015) expresses dissatisfaction with the type of compositionality exhibited in the ancient artisans game. Some of this dissatisfaction comes from the fact that it can only generate statements that are composite with respect to the senders’ dispositions. The receiver acquires its dispositions by reinforcing actions as if each composite statement is unitary; Narundi’s reinforcement of an action picked from the br urn has no direct effect on the contents of the bb urn or the rr urn. Call set of strategy profiles receiver-compositional if there is a term that is a component of at least two distinct statements (sender-compositionality) and changing the receiver’s dispositions for one of the statements directly results in changing the receiver’s dispositions towards the other statement(s) containing the given term.Footnote 2 E.g. the ancient artisans game is sender-compositional since r_ is a component of statements rb and rr; it is not receiver-compositional because the receiver’s dispositions towards the statement rb are defined by the contents of the rb urn, her dispositions towards rr are defined by the contents of the rr urn, and when a play results in reinforcement of dispositions towards one of those statement (i.e. adding a stone to the urn that was drawn from) there is no change in the contents of the other urn. The model described in Sect. 2.3 will exhibit receiver-compositionality by having a single urn that has an effect on the receiver’s dispositions towards two statements that contain the same term (the statements r_ and rb); when a stone is added to the shared urn, it directly effects the receiver’s dispositions towards both statements rather than only effecting dispositions towards the statement that was transmitted on the successful play.

Receiver-compositionality is intuitively desirable. Suppose someone, who already knows what “square" and “circle" mean, learns the appropriate response to hearing “bring the red circle". If she simultaneously fails to learn the appropriate response to hearing “bring the red square", then it seems doubtful that she has learned the meaning of “red" as a component part of the statement “bring the red circle". Conversely, if learning the appropriate response to “bring the red circle" causes a person to be disposed to act appropriately in response to “bring the red square", then this seems more reflective of “red" being treated as a component term. This is what receiver-compositionality allows.

It is worth attending to the reinforcment of dispositions when claiming that a term is a component of two distinct statements. If this is ignored, one might be tempted to claim that r is a component term of both br and rb in the ancient artisans story. However, there are strong reasons to reject this claim. One reason is that it is straightforwardly apparent that the meaning of r in br is entirely different than its meaning in rb. However, it could be argued that there is some connection between the meaning of an r from Devasena and an r from Valli since they both disposed to transmitting r for clay pots. This is merely an accidental connection in the meaning of r from each sender. That this is merely an accidental connection can be seen in a second reason for rejecting the claim. Consider a signaling game identical to the ancient artisans game but with one alteration; Valli wears green and yellow instead of blue and red. This game is isomorphic to the original and in simulations will lead to the same 73% run success rate. It is difficult to defend the claim that statements br and rb share a component term when there exists an isomorphic signaling system containing statements by and rg which clearly do not share a component term.Footnote 3 So why not avoid confusion and describe Devasena and Valli as using different pairs of colors from the start?

In maintaining the superficial similarity between Devasena and Valli’s terms, there is an immediately available extension of signaling game dynamics that creates a substantive identity between the terms used by distinct senders.Footnote 4 This extension is sender independence. An individual term X in a signaling game is sender independent if a receiver cannot condition her actions based on which sender transmitted X; this entails that the receiver typically performs the same action(s) irrespective of which sender transmitted the unitary X. In the pyow-hack game there will be two basic senders that can transmit a statement with a single P or H. Since the receiver will not be able to conditionalize on which basic sender transmitted the term, her dispositions towards a single P from basic sender A will be the same as her dispositions towards a single P from basic sender B; that is, the receiver will draw from (and on success reinforce) the same urns irrespective of which sender transmitted the single term. The power of sender independent terms will be more apparent after receiver-compositionality has been more thoroughly elaborated.

2.3 Receiver-Compositionality in a Hierarchical Game

Receiver-compositionality can be illustrated with an extension of the ancient artisans story. As trade networks expand, the three artisans are joined by industrialists Nekhbet and Hestia. Nekhbet sees a broader market context than Devasena and Valli; she determines whether only the material (clay or wood), only the form (pot or figurine), or both the material and form of the product are relevant. If only the material is relevant, Nekhbet only allows Devasena to observe the state of nature to determine what color to wear, while Valli wears an uninformative color; if only the from is relevant, then Nekhbet only allows Valli to observe nature to determine blue or red, and Devasena is uninformative; if both material and form are relevant she allows both Devasena and Valli to observe nature to determine what color to wear. When Narundi only sees a single term statement from Devasena and Valli (b_, r_, _b, or _r), then she draws at random with equal probability from either of the two corresponding urns; e.g. if Devasena wears red and Valli is uninformative, r_, then Narundi draws from either the rb or rr urn with equal probability. Hestia acquires supplies in bulk. She sees the signal from Devasena and Valli as well as Narundi’s draw from the corresponding urn. If only Devasena wears an informative color, then Hestia only attends to the material of Narundi’s draw and brings tools for both pots and figurines; e.g. if Narundi draws a wood pot token, Hestia brings wood and tools for both pots and figurines. If only Valli wears an informative color, then Hestia only attends to the form of Narundi’s draw and brings the corresponding tools along with both wood and clay. If both Devasena and Valli are informative, then Hestia brings material and tools corresponding to Narundi’s draw.

Fig. 2
figure 2

A partial pooling equilibrium for the hierarchical signaling game

Full size image

Barrett et al. (2018, 2019) show how the extended ancient artisans signaling system can be acquired through reinforcement learning using a hierarchical extension of the two-term two-sender one-receiver signaling game that exhibits receiver-compositionality. The hierarchical signaling game has two basic senders (e.g. Devasena and Valli), one executive sender (e.g. Nekhbet), one basic receiver (e.g. Narundi) and one executive receiver (e.g. Hestia). A state of nature features two binary properties (e.g. material and form) and a context (e.g. only material, only form, or both are relevant). In the game the executive sender sees the context and the basic senders see the properties. Correspondingly, the executive sender has three urns and the basic senders have four urns each, as they did in the previous game. The executive sender determines which of basic senders’ signals gets transmitted. She begins the game with three stones in each urn, a sender A stone, sender B stone, and a both stone. The basic receiver sees what signal was transmitted and has four urns as she did in the previous game. The executive receiver sees both what was transmitted (a single term from sender A, a single term from sender B, or two terms), and correspondingly has three urns. The executive receiver sees whether sender A, B, or both transmitted a signal and determines whether the basic receiver’s draw is interpreted as material, form, or both. Thus, the executive receiver begins the game with three urns, A, B, and Both, and each urn containing a material, form or both stone.

The set of strategy profiles depicted in Fig. 2 is called a partial pooling equilibrium. A set of strategy profiles is a partial pooling equilibrium if the players perform better than chance, but worse than optimal, and their strategy profiles are an equilibrium in the sense that, for any given urn, changing which type of ball is most populous will not improve the success rate. The partial pooling equilibrium depicted in Fig. 2 is worth highlighting because it is the first example of a signaling game exhibiting non-trivial compositionality; i.e. br indicates supply and demand for clay figurines, but this is not merely an intersection of what is indicated by b_ (which sometimes indicates wood) and _r (which sometimes indicates pots). In the hierarchical extension of the ancient artisans game, all optimal signaling systems are trivially compositional. It is not until the pyow-hack game that optimal signaling systems exhibit non-trivial compositionality.

Under basic Roth-Erev reinforcement learning, Barrett, Cochran and Skyrms’ hierarchical signaling game model exhibits run success rates around 20%.Footnote 5 This run success rate can be increased to around 97% when the reinforcement dynamics are supplemented with punishment via costly signals (Barrett et al., 2019, 2018). Since the focus of this paper is on how a particular type of compositionality can obtain, the details of stronger learning dynamics are omitted. However, it will be noted that the same type of reinforcement supplemented with punishment via costly signals produces similar gains in the pyow-hack signaling game model.

3 Sender Independent Terms in the Pyow-Hack Game

This section begins with a very brief description of putty-nosed monkey alarm calls, which were the inspiration for the pyow-hack game. This game is then described in Sect. 3.2. The monkeys provide a tangible motivation for what is otherwise a very abstract game. Their behavior also helps motivate some intuitions (discussed in Section 4.2) about how two terms can be composed together to generate different meanings based on their ordering. In turn, the pyow-hack game shows how a compositional signaling system with sensitivity to term ordering could be acquired by an organism that only has access to low rationality reinforcement learning dynamics. That said, this paper is not concerned with defending any particular interpretation of putty-nosed monkey alarm calls. The Lewis-Skyrms pyow-hack signaling game presented in Sect. 3.2 is shown (in Section 4.2) to exhibit a type of compositionality novel to the signaling game literature irrespective of the extent to which it accurately describes putty-nosed monkey behavior.

3.1 A Brief Description of Putty-Nosed Monkey Behavior

Cercopithecus nictitans martini, putty-nosed monkeys, are a West African species. They typically live in groups of 13-22 individuals comprised of one adult male with several females and dependent juveniles (Arnold & Zuberbühler, 2006). Their common predators are crowned eagles and leopards. Group leaders give different alarm calls that correlate fairly robustly with the presence of leopards and eagles. They also have a call associated with group movement (Arnold & Zuberbühler, 2006, 2008, 2013; Schlenker et al., 2016a, b).

Putty-nosed monkey alarm calls are comprised of two basic calls: a hack (H) and a pyow (P). These basic calls are strung together in sequences of varying length. A sequence of repeated hacks, perhaps HHHHHHHH, is associated with aerial predators (eagles) and invokes the behavior of looking up. A sequence of repeated pyows, perhaps PPPPP, is associated with ground predators (leopards). Behaviorally, the pyow call sequences are associated with moving towards the caller since ground predators rely on stealth and the monkeys can collectively scare off the predator (Arnold & Zuberbühler, 2013). Sequences of pyows followed by hacks, perhaps PPPPHH, are associated with group movement. Sequences of hacks followed by pyows, perhaps HHHHPPP, occur when a nearby eagle moves away from the group. Longer call sequences seem to correlate with more urgent contexts when signaling for predators and increased distance traveled when signaling group movement; behaviorally, this correlates respectively with faster reaction times and potentially moving longer distances (Arnold & Zuberbühler, 2012, 2013; Schlenker et al., 2016a).

Schlenker et al. (2016a) give a detailed overview of putty-nosed monkey alarm calls, and reasons for interpreting the calls as semantically compositional. Additionally, they propose some possible referential or imperative semantics for the alarm calls.Footnote 6 In developing a compositional semantics, Schlenker et al. make a particularly insightful observation about the relation between calls associated with ground predators and calls associated with group movement. Though over a shorter distance, the monkeys move towards the caller when the call for a ground predator is issued (so they can collectively mob the predator). This provides some reason for interpreting a “pyow" as contributing similar meaning to the ground predator call as a “pyow" contributes to a group movement call.

The pyow-hack signaling game will simplify things by only allowing six different statements in the game: P, PP, PH, H, HH, and HP. On this simplification, putty-nosed monkey behavior translates to the following call system. When a leopard is nearby, the group leader issues a P call, to which group members are disposed to move towards the group leader. When a leopard is very nearby, the group leader issues a PP call, to which group members are disposed to quickly move towards the group leader. When moving, the group leader issues a PH call, to which group members are disposed to move an extended distance towards the group leader. When an eagle is nearby, the group leader issues a H call, to which group members are disposed to look up. When an eagle is very nearby, the group leader issues a HH call, to which group members are disposed to quickly look up. When a nearby eagle is leaving, the group leader issues a HP call, to which group members are disposed to look up and then elsewhere.

3.2 The Pyow-Hack Game

The pyow-hack signaling game abstracts and simplifies away from several of the details of putty nose monkeys’ environment and behavior. Most noticeably, it only allows for call sequences of at most two signals. Like the Barrett, Cochran and Skyrms’s model (Barrett et al., 2019, 2018), it is a hierarchical signaling game consisting of an executive sender, two basic senders, an executive receiver, and a basic receiver.

In the pyow-hack game there are six states of nature: a leopard is nearby, a leopard is very near (urgent), an eagle is nearby, an eagle is very near (urgent), a nearby eagle is moving away, and the group is moving. There are six corresponding appropriate actions: move towards caller, quickly move towards caller, look up, quickly look up, look up and elsewhere, and move an extended distance towards caller.

The executive sender as well as the basic senders can observe the state of nature. The executive sender determines whether just one or both of the basic senders will transmit a signal. This corresponds with the executive sender having six urns, one for each state of nature. These urns contain two types of balls, single transmission balls and dual transmission balls. As in the previous games, all of the players’ urns start with one ball of each type. The basic senders each have six urns corresponding to the states of nature. The basic senders have two types of balls, P balls and H balls. On plays in which the executive sender draws a single transmission ball, it is determined at random with equal probability whether sender A or sender B transmits a signal.Footnote 7

Fig. 3
figure 3

A Signaling System for the Pyow-Hack Game

Full size image

The basic receiver has four urns: PP, PH, HP, and HH. When a single P is transmitted, it is determined at random with equal probability whether the basic receiver draws from the PP or PH urn.Footnote 8 When a single H is transmitted, it is determined at random with equal probability whether the basic receiver draws from the HP or HH urn. As in the previous hierarchical game, the basic receiver draws balls that can be given multiple interpretations by the executive. The basic receiver’s urns contain four types of balls labeled: (i) ‘quickly move towards caller’, (ii) ‘move an extend distance towards caller’, (iii) ‘quickly look up’, and (iv) ‘look up and elsewhere’. These labels are the complex interpretations that the executive can give to the balls. Type (i) and (ii) balls can be given the simple interpretation “move towards the caller". Type (iii) and (iv) balls can be given the simple interpretation “look up". Thus, the executive receiver has two urns, a single transmission urn and a dual transmission urn. Each of these urns has two types of balls, simple interpretation balls and complex interpretation balls.

Simple reinforcement learning (Roth-Erev) is the dynamic that was presented in Sect. 2.1. When a play is successful, drawn balls are returned to their urns and one additional ball of the type drawn is added to the urn that was drawn from for each player. On failures, balls are returned to the urns they were drawn from. Here’s an example play for the equilibrium depicted in Fig. 3:

  1. 1.

    Nature chooses a state at random with equal probability. Suppose the state of a nearby leopard is chosen.

  2. 2.

    The executive sender observes the state and chooses a ball at random with equal probability from her nearby leopard urn. Suppose the executive sender chooses a single transmission ball; this is the executive sender’s most likely choice in the example equilibrium.

  3. 3.

    Since the single transmission ball was drawn, either sender A or sender B is chosen at random with equal probability to transmit a signal. Suppose sender A is chosen.

  4. 4.

    Sender A observes the state of a nearby leopard. So, she draws at random with equal probability from her nearby leopard urn. Suppose she draws a P ball. Again, this is the most likely choice in the example equilibrium.

  5. 5.

    Given her draw, sender A transmits ‘P’.

  6. 6.

    Receiver C sees the ‘P’ and it is determined at random with equal probability whether she will draw from the PP urn or PH urn. Suppose it is determined that receiver C will draw from the PH urn.

  7. 7.

    Receiver C draws at random with equal probability from the PH urn. Suppose receiver C draws a (ii) ball. This is the ball that she is most likely to draw in the example equilibrium.

  8. 8.

    Receiver C’s draw is now interpreted by the executive receiver.

  9. 9.

    The executive receiver sees that only a single signal was transmitted and draws from her single urn. Suppose the executive receiver draws a simple ball. In the example equilibrium, this is her most likely draw.

  10. 10.

    Given that the executive receiver drew a simple ball, she interprets receiver C’s draw, (ii), as needing to move towards the caller. So this action is performed.

  11. 11.

    Since this is the correct action for the given state, this counts as a success.

  12. 12.

    Given the success, each player returns the ball that she drew along with an additional ball of the type that was drawn.

  13. 13.

    When a failure occurs, drawn balls are returned to the urns that they were drawn from.

This concludes a play of the game.

Simulating 1000 runs of the pyow-hack game, with \(10^7\) plays per run, produced the run success rate of 19.4%. This was calculated by measuring each run’s cumulative success rate, the number of successful plays divided by the total number of plays. This was calculated by counting a run as successful if it had a cumulative success rate above 0.92. This was an appropriate cutoff for determining whether a run was successful as \(0.92 > 5.5/6\). That is, a cumulative success rate greater than 0.92 is indicative of plays being successful for each of the six states of nature.

Under basic Roth-Erev reinforcement learning, the pyow-hack game has a run success rate of around 19%. This increases to around 58% when using costly signals analogous to Barrett, Cochran and Skyrms’ reinforcement with punishment via costly signals (Barrett et al., 2018, 2019). An even stronger learning dynamics, described by Barrett and Gabriel (2022), can give a run success rate of 94.3% (of 1000 runs, \(10^7\) plays per run, and 10 iterations of [+2, −9] reinforcement with iterated punishment). However, even on the weakest learning dynamics, it remains the case that when an optimal signaling system obtains, the compositionality is novel in that it is sensitive to the ordering of terms.

4 Discussion

4.1 Review of Technical Terms

Two types of compositionality are emphasized in this paper: (i) set of strategy profiles is sender-compositional if there is a term that is transmitted as a component of at least two distinct statements; (ii) a set of strategy profiles is receiver-compositional if there is a term that is a component of at least two distinct statements and changing the receiver’s dispositions for one of the statements directly results in changing the receiver’s dispositions towards the other statement(s) containing the given term. Receiver-compositionality allows a term to contribute similar dispositions to multiple statements that have the given term as a component part. Additionally, motivating some of the differences between the pyow-hack hierarchical game and the Barrett, Cochran, and Skyrms’ (Barrett et al., 2018, 2019) hierarchical game, a term is sender independent if, upon transmission of the unitary term, the receiver cannot condition her actions on which sender transmitted the term; this entails that, for a given set of strategy profiles, transmission of the unitary term typically results in the same action regardless of which sender transmitted it. The signaling game literature discusses a third type of compositionality defined by Schlenker et al. (2016b) and introduced to the signaling game literature by Steinert-Threlkeld (2020)Footnote 9: (iii) a set of strategy profiles is trivially compositional just in case complex expressions are always interpreted by intersection (generalized conjunction) of the meanings of the parts of the expression. It can be checked that optimal signaling systems for the Barrett, Cochran, and Skyrms hierarchical game are trivially compositional.Footnote 10

4.2 Order Sensitive Compositionality

Signaling systems for the pyow-hack game are not trivially compositional. If they were, since the terms are sender independent, HP would be associated with the same dispositions, as PH. But this cannot occur in a signaling system since the game only allows for six possible statements and requires distinct actions to be performed for each of the six states of nature. For a given set of strategy profiles, if transmitting HP and transmitting PH typically results in the same action being performed in response to either statement, then at most only five of the six states of nature can be mapped to the correct action by the senders’ and receiver’s strategy profiles. This is a quick method of demonstrating that compositionality exhibited in the pyow-hack game is different from the compositionality exhibited in the Barrett, Cochran, and Skyrms hierarchical game. However, it does not show how compositionality with sensitivity to term ordering obtains in the pyow-hack game.Footnote 11

Sensitivity to term ordering is allowed by the combination of both sender independent terms and receiver-compositionality. To see how this sensitivity is allowed, consider the signaling system diagrammed in Fig. 3. It is easy to see that PH and HP are associated with different dispositions, actions. PH is typically transmitted when the state of nature is group movement and typically results in the action of moving an extended distance towards the caller. HP corresponds with the nearby eagle leaving state of nature and the look up & elsewhere action. However, this does not necessarily entail that the compositionality is sensitive to term ordering because of the worry described at the end of Sect. 2.2. Recall that this worry raises the concern that the P in PH is not the same term as the P in HP, perhaps one is an A-tone P and the other is a B-tone P making them functionally distinct terms. To establish that the P in the PH statement is the same term as the P in the HP statement, it must be shown that there is a connection between the dispositions associated with the P term in PH statements and the P term in HP statements. The remainder of this section shows that there is such a connection, but also highlights why it is desirable for future models to strengthen the connection.

The meaning of a term in a Lewis-Skyrms signaling game model is best understood as being determined by the dispositions associated with that term.Footnote 12 A P alarm call means “leopard", “move towards caller", or has some meaning in between the two (à la Milikan 1984, 1995), both because the call is issued when a leopard is present and because the hearers respond as if a leopard is present when they hear the call. Suppose a group leader issues P calls when leopards are present and H calls when eagles are present; but, the monkeys hearing the calls look up at the sky when hearing P calls and move towards the leader in preparation for a leopard threat when hearing H calls. In this case, there is no signaling system and no communication. Neither the senders nor the receivers can unilaterally determine the meaning of a signal.

For the signaling system depicted in Fig. 3, a dispositional connection between the P’s in PH and HP can be understood as follows. A solitary P is correlated with the disposition to move towards the caller so the monkeys can collectively mob the leopard, and presumably this involves the monkeys looking in the direction they are moving or at the ground for a leopard, but not looking up at the sky. A PH call is correlated with group movement for an extended distance in the direction of the caller. So the dispositions associated with P and PH are similar in that they both involve movement towards the caller. An HP call is correlated with looking up and elsewhere. A solitary H is correlated with the disposition to look up, so it makes sense to take the P in an HP call with the disposition to look places other than the sky. So the P in an HP call also shares an overlap in associated dispositions with a solitary (Schlenker et al. 2016a) assert that it is plausible to think of putty-nosed monkey alarm calls as being analogous to semantics for conditionals. So, by loose analogy, one might think that P is associated with a set of possible worlds for which it is appropriate to move towards the caller or look towards the ground; H is associated with possible worlds for which it is appropriate to look up at the sky; and, if the nearest possible world to the center of the P set of worlds for which H is true is a different world than the nearest possible world to the center of the H set for which P is true, then this is why PH and HP have different meanings despite their component terms having the same meaning. This talk of possible worlds merely is intended to aid the reader’s intuitions and it is not being claimed that some possible worlds semantics obtains in the signaling system from Fig. 3. While this line of reasoning might help one see a connection in the dispositions associated with the P in PH and the P in HP, Sect. 2.2 showed that such connections can be merely accidental.

Certainly, the argument from Sect. 2.2 does not work for the Pyow-Hack game. If sender B’s P and H terms were replaced with Y and G, then there would be no justification for the basic receiver choosing from the same urns when receiving a solitary P from A as when receiving a solitary Y from B, which is an essential feature of the game. We know that a solitary P from A means the same thing as a solitary P from B because the receivers cannot condition their actions on which sender transmitted the term. More explicitly, one can see that the connection in dispositions is not merely accidental with the following chain of reasoning:

  • The P in PH statements is dispositionally connected to the P in solitary P statements from A by receiver-compositionality. In both the corresponding group movement and leopard states (when A happens to be the solitary transmitter) successful action reinforces the prevalence of (ii)-balls in receiver C’s PH urn.

  • Since terms are sender independent solitary P statements transmitted by sender A are associated with the same dispositions as solitary P statements transmitted by sender B.

  • The P in solitary P statements from B is connected to the second P in PP statements by receiver-compositionality. In both the corresponding leopard (when B happens to be the solitary transmitter) and urgent leopard states, successful action reinforces the prevalence of (i)-balls in receiver C’s PP urn.

  • Finally, there is a connection in dispositions between the second P in PP statments and the P in HP statements since both are transmitted by the same functional component, sender B.

Now if it were possible for just the receivers or just the senders to unilaterally determine the meaning of statements in the game, then this chain of reasoning, relying on features of both the senders and receivers, would be problematic. However, since acquisition of a signaling system requires both senders and receivers to have dispositions consistent with each other, there is a substantive connection between the P in PH and the P in HP.

Still, the fact that features of both senders and receivers are necessary to trace a connection between the P in PH and the P in HP shows that neither the senders in isolation nor the receivers in isolation can be said to represent the connection between PH and HP. Worse, consider Fig. 3 with the following changes: swap the contents of C’s HP and HH urns, likewise swap the contents of B’s urgent eagle and eagle leaving urns. This results in an optimal signaling system (which can and has obtained under the same learning dynamics) where HP means urgent eagle/look up quickly and HH means eagle leaving/look up and elsewhere. In this signaling system there is no longer an overlap in the behaviors associated with HP and those associated with a solitary P. However, it should be noted that it is not possible to produce an optimal signaling system that breaks the dispositional connection between P and PP nor the connection between H and HH. This is because the way in which the model implements receiver-compositionality (via C’s balls that have two interpretations) guarantees that, in optimal signaling systems, a single term transmission X will always be dispositionally connected with XP and XH statements.

These considerations suggest at least two ways in which future models could attempt to improve on the pyow-hack game given in this paper. First, a model could attempt to modify the senders to better represent the connection between states of nature associated with similar actions. For example, the game could be modified such that for any state X \(\in \) {leopard very near, leopard nearby, group is moving, nearby eagle leaving} there is some small probability that the basic senders draw at random from one of the other three urns in the set rather than from the X urn. This would have a nominal negative effect on the success rate of a signaling system and would make signaling systems where P means leopard and HP means eagle leaving more likely to obtain than signaling systems where P means leopard and HP means urgent eagle. Second, a model could focus on attempting to make a single player represent a connection in meaning between the P in PH and P in HP. For example, one could modify the game to have receiver C, upon receiving a solitary P, draw at random with equal probability from the PP, PH or HP urns. This would in some sense force a connection between the meaning of PH and HP.

However both of these naive examples have down sides. The first example still results in neither the senders in isolation nor the receivers in isolation capturing the connection in the meaning of P in PH and the P in HP; additionally, it is still possible (just less probable) for a signaling system to obtain where P means leopard and HP means urgent eagle. The second example results in a significant negative impact on every set of strategy profiles’ success rate and, in the limit, the contents of the HP urn will only nominally overlap with the contents of the PH and PP urns since receiver C has a strictly greater probability of visiting the HP urn for either a solitary H or an HP than her probability of visiting the HP urn for a solitary P.

Despite the noted issues, it is clear that the pyow-hack game exhibits a novel type of compositionality that advances our understanding of signaling games. The conjunction of sender independent terms with receiver-compositionality does provide reason, in optimal signaling systems, to consider the P in PH as being the same term as the P in HP. The model’s introduction of sender independent terms disallows the argument by isomorphism, given in Sect. 2.2. In contrast with this, it is easy to see that the prior hierarchical model given by Barrett et al. (2018, 2019) is isomorphic with a model where B’s terms are y and g (rather than b and r) since both receivers in that model condition their actions on which sender transmitted a unitary term. However, if one tried to do the same with the pyow-hack game it would be mysterious why the receivers’ dispositions towards P were the same as their dispositions towards Y. While this paper borrows and explicates receiver-compositionality from the prior hierarchical signaling game, the pyow-hack game does show how a novel type of compositionality can obtain.