Inverse Linking, Possessive Weak Definites and Haddock Descriptions: A Unified Dependent Type Account

Abstract

This paper proposes a unified dependent type analysis of three puzzling phenomena: inversely linked interpretations, weak definite readings in possessives and Haddock-type readings. We argue that the three problematic readings have the same underlying surface structure, and that the surface structure postulated can be interpreted properly and compositionally using dependent types. The dependent type account proposed is the first, to the best of our knowledge, to formally connect the three phenomena. A further advantage of our proposal over previous analyses is that it offers a principled solution to the puzzle of why both inversely linked interpretations and weak definite readings (in contrast to Haddock-type readings) are blocked with certain prepositions.

1 Introduction

This paper focuses on three types of complex DPs: inverse linking constructions (May 1978, 1985; Larson 1985; Zimmermann 2002; Kobele 2010), possessive definite descriptions (Löbner 1985, 2011; Poesio 1994; Barker 2005; Peters and Westerståhl 2013) and Haddock descriptions (Haddock 1987; Champollion and Sauerland 2011; Sailer 2014; Bumford 2017). Inverse linking constructions, e.g., a representative of every country, allow the inversely linked interpretation in which the embedded quantifier phrase (every country) takes scope over the embedding one (a representative). Scoping out of DP islands represents an unresolved difficulty for standard LF-based scope-assignment strategies (see, e.g., Kratzer and Heim 1998; Zimmermann 2002). Possessive definite descriptions (possessive definites) and Haddock descriptions (Haddock definites) pose a puzzle for standard theories of definiteness based on uniqueness. Possessive definites, e.g., the student (sister, son) of a linguist, can be used in a situation in which linguists in question have more than one student (sister, son)—they carry no implication that only one individual satisfies the content of the description. Haddock definites, e.g., the rabbit in the hat, can be used successfully in contexts with multiple salient hats and multiple salient rabbits as long as there is a single rabbit-in-a-hat pair—they carry no standard requirements that there be exactly one hat, with exactly one rabbit in it. All three phenomena are nominal constructions involving quantification and relations that are not functional but (possibly) one-to-many (‘representing’, ‘being a sister of’, etc.). We shall argue that dependent types are well suited to modeling the interaction of non-functional relations and quantification.

Dependent type theoretical frameworks (Martin-Löf 1975; Martin-Löf and Sambin 1984; Makkai 1995) have been used to model linguistic phenomena of central importance, e.g., unbound anaphora (Ranta 1994; Fernando 2001; Cooper 2004; Grudzińska and Zawadowski 2014; Bekki 2014), lexical phenomena such as selectional restrictions and coercions (Asher 2011; Luo 2012; Chatzikyriakidis and Luo 2017b), adjectival and adverbial modification (Chatzikyriakidis and Luo 2017a) and long-distance indefinites (Grudzińska and Zawadowski 2017d). This paper argues that the three puzzling readings (inversely linked interpretations, weak definite readings in possessives and Haddock-type readings) provide another compelling example of application of dependent types to the study of natural language semantics. Specifically, we propose that the three readings under consideration have the same underlying surface structure [introduced and independently motivated in Zimmermann (2002) and Barker (2005)], and that the surface structure postulated can be interpreted properly and compositionally using dependent types. Other directly compositional (non-movement) accounts of the phenomena in question have been proposed [for inverse linking, see Hendriks (1993); Barker (2002); for possessive weak definites, see Löbner (1985); Barker and Shan (2014); for Haddock definites, see Haddock (1987); Bumford (2017)]. However, to the best of our knowledge, our proposal is the first to formally connect the three phenomena. A further advantage of our dependent type account over previous directly compositional analyses is that it offers a principled solution to the puzzle of why both inversely linked interpretations and weak definite readings (in contrast to Haddock-type readings) are blocked with certain prepositions, e.g with, as in someone with every known skeleton [example from May and Bale’s (2005)] or the student with a brown jacket [example from Poesio’s (1994)].

In the rest of the paper we shall show that our semantic framework with dependent types provides us with uniform and adequate mechanisms to model the three puzzling phenomena. The structure of the paper is as follows. In Sect. 2, we explain the main features of our semantic framework [as presented in Grudzińska and Zawadowski (2014, 2017a)], most notably the concept of type dependency and type-theoretic notion of context. Section 3 puts forth our dependent type analysis of inverse linking constructions [key parts of this section were already presented in Grudzińska and Zawadowski (2017b), here we expand on this material with more technical details and explanations]. In Sect. 4, we present a new treatment of possessive weak definites, and in Sect. 5, we propose our dependent type solution to Haddock’s puzzle. Section 6 offers a principled answer to the puzzle of why inversely linked interpretations and weak definite readings are blocked with certain prepositions (in contrast to Haddock-type readings). Section 7 explains the remaining details of our compositional analysis, before concluding in Sect. 8.

2 Semantics with Dependent Types

In this section, we give an introduction to the main features of our semantic framework with dependent types (emphasizing those relevant for this paper), and explain how common nouns (sortal and relational), quantifier phrases (QPs) and predicates are to be interpreted in this framework.

2.1 Context and Type Dependency

The concept of dependent types is at the heart of dependent type theoretical frameworks (Ranta 1994; Luo 2012; Bekki 2014; Fernando 2001; Cooper 2004). Our semantic system can be seen as many-sorted in that it contains many sorts (types) (as compared with Montague semantics which is single-sorted in that it has one basic type e of all entities—strictly speaking, it has also another ‘auxiliary’ basic type t of truth values, and a recursive definition of functional types). The variables of our system are always typed: $x:X, y:Y, \ldots$; types are interpreted as sets: $\Vert X\Vert , \Vert Y\Vert , \ldots$ In our system, types can depend on the variables of other types, e.g., if x is a variable of the type X, we can have type Y(x) depending on the variable x. The fact that Y is a type depending on X is to be modeled as a function:

$$\begin{aligned} \Vert \pi \Vert : \Vert Y\Vert \rightarrow \Vert X\Vert , \end{aligned}$$

the intended meaning being that each type Y(x) is interpreted as the fiber $\Vert Y\Vert (a)$ of $\Vert \pi \Vert$ over $a\in \Vert X\Vert$ (the inverse image of the singleton $\{a\}$ under $\Vert \pi \Vert$). If X is a type and Y is a type depending on X, we can also form dependent sum types $\varSigma _{x:X} Y(x)$ (whose interpretation consists of pairs $\langle a, b\rangle$ such that $a\in \Vert X\Vert$ and $b\in \Vert Y\Vert (a)$) and dependent product types $\varPi _{x:X} Y(x)$ (whose interpretation consists of functions which assign to each $a\in \Vert X\Vert$ an element of $\Vert Y\Vert (a)$). For the purposes of this paper, we only need $\varSigma$-types; $\varSigma _{x:X} Y(x)$ is to be interpreted as the disjoint sum of fibers over elements in $\Vert X\Vert$:

$$\begin{aligned} \Vert \varSigma _{x:X} Y(x)\Vert \;= \; \bigsqcup _{a\in \Vert X\Vert } \Vert \pi \Vert ^{-1}(a) \end{aligned}$$

i.e., it is (in bijective correspondence with) the set $\Vert Y\Vert$.

Context is another core trait of dependent type theoretical frameworks. For us context is (a linearization of) a partially ordered set of type declarations of the (individual) variables such that the declaration of a variable x of type X precedes the declaration of a variable y of type Y(x):

$$\begin{aligned}\varGamma = x: X, y: Y(x), z: Z(x,y), u:U, \ldots \end{aligned}$$

In the above example, type Y depends on the variable x of type X; type Z depends on the variables x and y of types X and Y, respectively; and types X and U are constant types (i.e., they do not depend on any variables).¹ Having a context $\varGamma$ as above, we can declare a new type T in that context and a new variable of this type in that context, and extend the context by adding this new variable declaration. The empty context $\emptyset$ is a valid context. If $\varGamma$ is a valid context, t is a new free variable (i.e., $t \not \in FV(\varGamma )$), and T is a type in the context $\varGamma$, then the extension of $\varGamma$ by (a free variable of) the type T, denoted $\varGamma , t: T$, is also valid.

Contexts can be represented as dependence graphs. A dependence graph for the context $\varGamma$ is a graph that has types occurring in $\varGamma$ as vertices, and an edge $\pi _{Y,x} : Y \rightarrow X$ for every variable declaration $x:X(\ldots )$ in $\varGamma$ and every type $Y(\ldots , x,\ldots )$ occurring in $\varGamma$ that depends on x:

The corresponding semantic notion is that of a dependence diagram. The dependence diagram for the context $\varGamma$ associates to every type X in $\varGamma$ a set $\Vert X\Vert$, and to every edge $\pi _{Y,x} : Y \rightarrow X$, a function $\Vert \pi _{Y,x}\Vert : \Vert Y\Vert \rightarrow \Vert X\Vert$, so that whenever we have a triangle of edges (as on the left), the corresponding triangle of functions commutes (i.e., $\Vert \pi _{Z,x}\Vert = \Vert \pi _{Y,x}\Vert \circ \Vert \pi _{Z,y}\Vert$):

The interpretation of the context $\varGamma$, the dependence diagram, gives rise to the parameter space $\Vert \varGamma \Vert$ which is the limit² of the dependence diagram (i.e., the set of compatible n-tuples of the elements of the sets corresponding to the types involved).³ For the context $\varGamma = x: X, y: Y(x)$, its parameter space $\Vert \varGamma \Vert$ is $\Vert \varSigma _{x:X} Y(x)\Vert$.

For more technical details and explanations about our notion of context, we refer the reader to our system presented in Grudzińska and Zawadowski (2017a).

2.2 (Relational) Common Nouns as (Dependent) Types

A difference between our framework and Montague semantics lies in the interpretation of common nouns, sortal and relational. In the Montagovian setting sortal common nouns (e.g., man, country) are modeled as predicates/one-place relations (expressions of type $\langle e,t \rangle$). In our framework they are treated as types, e.g., man is modeled as the type M(an) and extends the context by adding a new variable m of the type M, with M being interpreted as the set $\Vert M\Vert$ of men. In the Montagovian setting relational common nouns (e.g., representative, sister) are interpreted as two-place relations (expressions of type $\langle e, \langle e,t \rangle \rangle$). Our framework allows us to treat relational common nouns as dependent types, e.g., representative (as in a representative of a country) is modeled as the dependent type:

$$\begin{aligned} c:C \vdash R(c): \textsf {Type}, \end{aligned}$$

and extends the context by adding a variable r of type R(c):

$$\begin{aligned} c:C, r:R(c), \end{aligned}$$

with the interpretation being as follows:

Here if we interpret type C as the set $\Vert C\Vert$ of countries, then we can interpret R as the set of the representatives of the countries in $\Vert C\Vert$, i.e., as the set of pairs:

$$\begin{aligned} \Vert R\Vert =\{ \langle a,p\rangle : p \; \mathrm{is\; the\; person\; from \; the\; country\; } a \} \end{aligned}$$

equipped with the projection $\Vert \pi _{R,c}\Vert : \Vert R\Vert \rightarrow \Vert C\Vert .$ The particular sets $\Vert R\Vert (a)$ of the representatives of the country a can be recovered as the fibers of this projection (the inverse images of $\{a\}$ under $\Vert \pi _{R,c}\Vert$):

$$\begin{aligned} \Vert R\Vert (a) = \{r \in \Vert R\Vert : \Vert \pi _{R,c}\Vert (r)=a\}. \end{aligned}$$

The interpretation of the structure:

$$\begin{aligned} c:C, r:R(c) \end{aligned}$$

gives us access to the sets (fibers) $\Vert R\Vert (a)$ of the representatives of the particular country a only. To form the set of all representatives, we need to use $\varSigma$ type constructor which takes the sum of fibers of representatives over countries in $\Vert C\Vert$:

$$\begin{aligned} \Vert \varSigma _{c:C} R(c)\Vert \;= \; \bigsqcup _{a\in \Vert C\Vert } \Vert \pi _{R,c}\Vert ^{-1}(a). \end{aligned}$$

Our system makes no use of assignment functions; variables serve to determine dependencies and act as an auxiliary syntactic tool to determine how the operations combining interpretations of QPs and predicates are to be applied. Types, as opposed to predicates, denote collections which can be quantified over.

2.3 QPs and Predicates in Context

Both quantifier phrases and predicates are defined in contexts. In a quantifier phrase:

$$\begin{aligned} \varGamma , y:Y(\mathbf {x}) \vdash Q_{y:Y(\mathbf {x})} \end{aligned}$$

the variable y is the binding variable and the variables $\mathbf {x} = x_1, \ldots , x_k$ are indexing variables. We have a polymorphic interpretation of quantifiers. A generalized quantifier associates to every set Z a subset of the power set of Z:

$$\begin{aligned} \Vert Q\Vert (Z)\subseteq {{\mathcal {P}}}(Z). \end{aligned}$$

In the standard Montagovian setting QPs are interpreted over the universe of all entities E Montague (1973). For example, some country denotes the set of subsets of E:

$$\begin{aligned} \Vert \exists x: \textit{country x}\Vert = \{X \subseteq E: \Vert country\Vert \cap X \ne \emptyset \}. \end{aligned}$$

In our semantic framework QPs are interpreted over various types. For example, some country is interpreted over the type Country (given in the context), i.e., some country denotes the set of all non-empty subsets of the set of countries:

$$\begin{aligned} \Vert \exists \Vert (\Vert Country\Vert ) = \{X\subseteq \Vert Country\Vert : \quad X \ne \emptyset \}. \end{aligned}$$

Quantification is also allowed over fibers, e.g., we can quantify existentially over the fiber of the representatives of France, as in some representative of France:

$$\begin{aligned} \Vert \exists \Vert (\Vert R\Vert (\textit{France}))= \{X\subseteq \Vert R\Vert (\textit{France}) : \quad X \ne \emptyset \}. \end{aligned}$$

We also have a polymorphic interpretation of predicates. If we have a predicate P defined in a context $\varGamma$:

$$\begin{aligned} \varGamma \vdash P(x_1, \ldots , x_n), \end{aligned}$$

then, for any interpretation of the context $\varGamma$, it is interpreted as the subset of its parameter space, i.e., $\Vert P\Vert (\Vert \varGamma \Vert )\subseteq \Vert \varGamma \Vert$.

In this system, dependencies given in the context determine the relative scoping of quantifiers. For example, in the context:

$$\begin{aligned} \varGamma = x: X, y: Y(x), z: Z(x,y), u:U, \ldots \end{aligned}$$

the interpretation of a sentence with two QPs where $Q_{1 \; x:X}$ outscopes $Q_{2 \; y: Y(x)}$ ($Q_{1 \; x:X} > Q_{2 \; y: Y(x)}$) is available, and the interpretation where $Q_{2 \; y: Y(x)}$ outscopes $Q_{1 \; x:X}$ ($Q_{2 \; y: Y(x)} > Q_{1 \; x:X}$) is not available because the occurrence of the indexing variable x in Y(x) is outside the scope of the second binding occurrence of x next to $Q_1$. A global restriction on variables is that each occurrence of an indexing variable be preceded by a binding occurrence of that variable—free undeclared variables are illegal (for more on this restriction, see Grudzińska and Zawadowski 2017a). As a consequence, this principle considerably restricts the number of possible readings for sentences involving multiple quantifiers and will have a major role to play in our account of the three puzzling phenomena to be discussed in the sections to follow: inversely linked interpretations, weak definite readings in possessives and Haddock-type readings.

3 Inverse Linking Constructions

Inverse linking constructions (ILCs) refer to complex DPs which contain an embedded QP, as in (1):

• (1) A representative of every country

ILC in (1) can be understood to mean that there is a potentially different representative for each country, i.e., it allows an inverse reading in which every country outscopes a representative. Under standard LF-based analyses, the inverse reading of ILCs is attributed to the application of quantifier raising (QR). QR replaces the QP every country with the coindexed trace ($t_1$), and adjoins it at DP

Standard analyses of ILCs have been claimed problematic on a number of grounds. For example, there is contradictory evidence regarding the landing site of the raised QP [adjunction to DP (see the tree above) versus adjunction to S—for the discussion, see Zimmermann (2002)]. We propose an alternative non-movement analysis of inverse readings. Following Löbner (1985, 2011), we distinguish between functional common nouns (e.g., mother, head, age) and relational common nouns (e.g., representative, sister, son). Relational nouns involve relations that are not functional but (possibly) one-to-many. Under our analysis, relational nouns are treated as dependent types. For example, as explained in detail above, representative (as in a representative of a country) is modeled as the dependent type:

$$\begin{aligned} c:C \vdash R(c): \textsf {Type}, \end{aligned}$$

and extends the context by adding a variable r of type R(c):

$$\begin{aligned} c:C, r:R(c). \end{aligned}$$

By quantifying over c : C, r : R(c), we get the inverse ordering of quantifiers:

$$\begin{aligned} \forall _{c:C} \exists _{r:R(c)}. \end{aligned}$$

The interpretation where $\exists$ outscopes $\forall$, $\exists _{r:R(c)}\forall _{c:C}$, is not available because the indexing variable c (in R(c)) is outside the scope of the binding occurrence of that variable (see our global restriction on variables introduced above). By making the type of representatives dependent on (the variables of) the type of countries, our analysis forces the inversely linked reading without positing any extra scope mechanisms.

More precisely, we propose the following analysis of the inverse reading for ILC:

QPP stands for the PP containing the QP (as in Zimmermann 2002). The QPP of every country is right-adjoined to the QP consisting of the head nominal (a representative). The head nominal representative is modeled as the dependent type:

$$\begin{aligned} c:C \vdash R(c): \textsf {Type}, \end{aligned}$$

and extends the context by adding a variable r of type R(c):

$$\begin{aligned} c:C, r:R(c), \end{aligned}$$

country is modeled as the type C. The preposition of is a purely syntactic marker signalling that country is a type on which representative depends⁴ The interpretation of the structure:

$$\begin{aligned} c:C, r:R(c) \end{aligned}$$

gives us access to the sets (fibers) $\Vert R\Vert (a)$ of the representatives of the particular country a only. We use $\varSigma$ type constructor to form the type of all representatives $\varSigma _{c:C} R(c)$. The complex DP a representative of every country is interpreted as the complex quantifier living on the set of all representatives $\Vert \varSigma _{c:C} R(c)\Vert$:

$$\begin{aligned}&\Vert \forall _{c:C} \exists _{r:R(c)}\Vert = \{X \subseteq \Vert \varSigma _{c:C} R(c)\Vert : \{a \in \Vert C\Vert :\{b \in \Vert R\Vert (a): b \in X \} \\&\qquad \in \Vert \exists \Vert (\Vert R\Vert (a))\}\in \Vert \forall \Vert (\Vert C\Vert )\}, \end{aligned}$$

i.e., it denotes the set of the subsets of the set of representatives such that the set of countries such that each country has at least one representative in the corresponding fiber of representatives is the set of all countries (we refer to this kind of quantification as quantifying ‘fiber by fiber’).

ILC in (1) can be also understood to mean that there is some one person who represents all the countries, i.e., it allows a surface reading in which a representative outscopes every country.⁵ To capture this reading, we propose that representative be treated standardly as a predicate, interpreted as the subset of $\Vert P(erson)\Vert \times \Vert C(ountry)\Vert$ (and not as a dependent type). Quantifying universally the country-argument, we obtain a type whose interpretation is the set of individuals who represent all the countries. By quantifying existentially over this set, we get the surface reading. More specifically, we propose the following analysis of the surface reading for ILC:

The QPP stands in the sister position to the head nominal representative. Our proposal is that the relational noun representative is now interpreted as the subset of $\Vert P(erson)\Vert \times \Vert C(ountry)\Vert$. The complex NP (noun modified by the postnominal QPP) representative of every country is then interpreted as the type/set of individuals who represent all the countries: $\{p: \{c: \langle p, c\rangle \in \Vert Represent\Vert \} \in \Vert \forall \Vert (\Vert C\Vert )\}$, and the DET a quantifies existentially over this set, yielding the surface ordering of quantifiers.

One apparent problem for our proposal is that inverse readings are also available for ILCs involving sortal nouns, as in a man from every city. Our solution is that a sortal noun like man can undergo a ‘sortal-to-relational’ shift, resulting in the (IR)-structure:

Partee and Borschev (2012) emphasize the permeability of the boundary between sortal an relational nouns and the fact that nouns can often be coerced to cross this border. In this case, the relational use of the sortal noun man can be coerced by the presence of the locative preposition from. Such prepositions specify the local position or origin of an entity and since entities do not occur at more than one place simultaneously, the dependency c : C, m : M(c) is likely to be a preferred interpretation for man from (for any city, there is a set (fiber) of the men from that city). Our analysis of the above structure is then exactly like the one described for the inverse reading of a representative of every country.

The two structures for the inverse and surface readings [structure (IR) and (SR), respectively] were postulated and motivated by Zimmermann (2002). Zimmermann argues that there is syntactic evidence for a different SS for the inverse reading, namely PPs containing QPs that give rise to inverse readings cannot freely change places with regular postnominal modifiers [e.g., relative clauses (RCs)] but must be DP-final, as illustrated by the examples below:

• (a) One person [RC who was famous] [QPP from every city] was invited.

• (b) $\sharp$ One person [QPP from every city] [RC who was famous] was invited.

Sentence (a) can be understood to mean that every city x is such that one famous person from x was invited, while sentence (b) is semantically odd—it only allows a surface reading saying that one person who came from every city and who was famous was invited. Inverse readings are possible when QPPs follow RCs [as in (a)], while non-final QPPs give rise to surface readings only [as in (b)]. This asymmetry is unexpected on the LF-based analysis since all postnominal modifiers (QPPs, RCs) have the same syntactic status, i.e., they stand in sister position to the head nominals. Based on this argument, Zimmermann proposes a different structure for the inverse reading, where the QPP (of every country) is not a regular postnominal modifier [as in (SR)] but is right-adjoined to the QP a representative [as in (IR)]. On the semantic side, Zimmermann proposes to derive inverse readings via a non-compositional reinterpretation procedure (for more on this, see Zimmermann 2002) In our analysis, we adopt Zimmermann’s position that ILCs are structurally ambiguous at surface structure: the two readings derive from the two surface structures distinguished by the syntactic position of the QPP. The advantage of our dependent type account over Zimmermann’s analysis is that it interprets the surface structure for the inverse reading in a fully compositional way. We shall now see that the same two structures were independently introduced and motivated for possessive definites.

4 Possessive Definites

Possessive definites (PDs) refer to complex definite DPs which contain an of-PP, as in (2):

• (2) The student (sister, son) of a linguist

As observed by Löbner (1985, 2011) and Barker (2005), PDs can be used in a situation in which linguists in question have more than one student, sister or son (the nouns involved are relational, not functional). Such ‘weak uses’ represent a difficulty for standard approaches to definiteness based on uniqueness.⁶ Uniqueness theories assume that definite determiner requires uniqueness (relativized to the discourse situation), i.e., the object referred to by a definite description must be the only object (in the discourse situation) that satisfies the content of the description. The uniqueness requirement is standardly taken to be a presupposition and the is defined as a partial function

$$\begin{aligned} \Vert the\Vert = [\lambda P: \exists !x P(x). \iota x P(x)], \end{aligned}$$

i.e., a function from properties P—defined only if there is exactly one x such that P(x) ($\exists !x P(x)$)—to the unique x such that P(x) ($\iota x P(x)$ is a referring expression standing for the unique individual who satisfies P). We propose to use the following type-theoretic variation of this definition (one that lifts the to the quantifier-type interpretation and does not introduce partiality into the system)

$$\begin{aligned} \Vert the\Vert (\Vert X\Vert ) \;= \; \left\{ \begin{array}{ll} \{\Vert X\Vert \} &{} \text{ if } \overline{\Vert X\Vert } = 1 \\ \emptyset &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

i.e., the respective definite denotes $\{\Vert X\Vert \}$ if there is a unique element in $\Vert X\Vert$, and the empty set, otherwise.

Barker (2005) distinguishes between strong (theoretically unproblematic) and weak readings of PDs, and postulates that the two readings derive from the two surface structures (analogous to the two structures for the two readings of ILCs, postulated independently by Zimmermann)

On the strong reading (SR), student combines with the of-phrase resulting in a property P corresponding to the set of individuals who are students of a linguist; the combines then with this set to yield one individual from this set (Barker 2005). Similarly, under our dependent type theoretical analysis, the complex NP (noun modified by the of-PP) student of a linguist is interpreted as the type/set of individuals who are students of a linguist: $\{s: \{l: \langle s, l\rangle \in \Vert Student_{of}\Vert \} \in \Vert \exists \Vert (\Vert L\Vert )\}$, and the DET the quantifies over this set, yielding the singleton consisting of a single student (if there is a unique student of a linguist), and the empty set, otherwise.

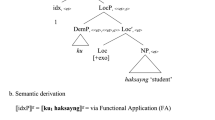
On the weak reading (WR), as argued in Barker (2005), the first combines with the relational noun student, and then with the of-PP. On the semantic side, the idea is that the interpretation of the is shifted (via the Geach rule) and combined with the interpretation of student via function composition, and only then applied to the interpretation of the of-PP. This order of combination gives the same result as in the previous analysis (corresponding to the (SR)-structure). Barker claims that the difference between the two analyses consists in the presuppositions triggered. In the (SR)-case, the requirement is that the complex NP as a whole (student of a linguist) describes a unique object in the discourse situation. In the (WR)-case, the requirement is that the referent of the relational student is determined uniquely relative to the possessor argument (a linguist); a successful use of a PD ‘is one that provides enough information for the listener to pick out the intended kind of object’, i.e., the student of a linguist that the speaker has in mind. While no formalization of this intuitive analysis of the (WR)-case was proposed in Barker (2005), our dependent type analysis provides a way of expressing this intuition formally. Under our account, the head nominal student is modeled as the dependent type:

$$\begin{aligned} l:L \vdash S(l): \textsf {Type}, \end{aligned}$$

and extends the context by adding a variable s of type S(l):

$$\begin{aligned} l:L, s:S(l). \end{aligned}$$

The complex DP the student of a linguist is interpreted as the complex quantifier living on $\Vert \varSigma _{l:L} S(l)\Vert$ (an element of $\Vert \varSigma _{l:L} S(l)\Vert$ is a pair $\langle a, b\rangle$ such that $a\in \Vert L\Vert$ and $b\in \Vert S\Vert (a)$):

$$ \begin{aligned}&\Vert \exists _{l:L} the_{s: S(l)}\Vert \\&\quad = \{X \subseteq \Vert \varSigma _{l:L} S(l)\Vert : \{a \in \Vert L\Vert : \Vert S\Vert (a) = 1 \;\ \& \;\ \Vert S\Vert (a) \subseteq X \} \in \Vert \exists \Vert (\Vert L\Vert )\}, \end{aligned}$$

i.e., it denotes the set of specific student-linguist pairing(s) if there is at least one linguist a in $\Vert L\Vert$ such that the fiber over a, $\Vert S\Vert (a)$, contains only one student (that the speaker has in mind). Otherwise, it denotes the empty set.

Two more remarks are in order. First, in this section we only considered PDs with an indefinite possessor (object of the genitive of) such as the student of a linguist. In the literature there is a disagreement over whether weak definite readings are also available for PDs with a definite possessor such as the student of the linguist. Contra to Poesio (1994), Barker claims that PDs with definite possessors allow the weak interpretation (Barker 2005). We shall come back to this problem after discussing our account of Haddock definites. Second, some authors observed that ILCs and PDs are systematically subject to the so-called ‘narrowing’, i.e., the universal quantifier of the ILC a representative of every country is restricted to countries that delegate (some) representatives, and the existential quantifier of the PD the student of a linguist is restricted to linguists who have students (Barker 1995; Champollion and Sauerland 2011; Peters and Westerståhl 2013; Sailer 2014). The narrowing mechanism is sometimes viewed as a pragmatic process of accommodation (Lewis 1979; Champollion and Sauerland 2011) and sometimes built into the truth conditions of the possessive definite (Peters and Westerståhl 2013) or the inverse linking construction (Sailer 2014). In this paper, we do not integrate narrowing into our account. In particular, we shall show that our analysis allows us to derive Haddock-type readings without the recourse to narrowing in either semantic or pragmatic sense [unlike in the proposals in Champollion and Sauerland (2011); Sailer (2014)].

5 Haddock Definites

Haddock definites (HDs) refer to embedded definites, as in (3)

• (3) The rabbit in the hat

HDs can be used successfully in contexts with multiple salient hats and multiple salient rabbits as long as there is a single rabbit-in-a-hat pair. There is an unresolved controversy over the precise requirement on the successful use of HDs in such contexts. In Champollion and Sauerland’s movement analysis (Champollion and Sauerland 2011), the rabbit in the hat presupposes that the number of hats that contain exactly one rabbit is exactly one. In Bumford’s dynamic account (Bumford 2017), the rabbit in the hat has a stronger presupposition that the number of hats that contain at least one rabbit is exactly one. Under the former analysis the rabbit in the hat can be used felicitously in the context in which one hat contains one rabbit and another hat contains two rabbits, while under the latter analysis the use of the description is infelicitous in this context (since it has three rabbit-hat pairs). It will be shown that both variants can be accounted for using our dependent type analysis.

As with the previous cases of ILCs and PDs, HDs have been observed to be ambiguous between absolute readings (with the standard unproblematic uniqueness requirements that there be exactly one hat, with exactly one rabbit in it) and Haddock-type relative readings (Bumford 2017). Again, we propose that the two readings of HDs derive from the two surface structures (analogous to the previous ones postulated independently by Zimmermann and Barker for ILCs and PDs, respectively):

On the absolute reading (AR), the hat is interpreted as the strong definite:

$$\begin{aligned} \Vert the\Vert (\Vert Hat\Vert ) \;= \; \left\{ \begin{array}{ll} \{\Vert Hat\Vert \} &{} \text{ if } \overline{\Vert Hat\Vert } = 1\\ \emptyset &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

The hat comes with the standard requirement that there be a unique hat. The head nominal rabbit combines with the in-phrase resulting in the type/set of rabbits in the hat; the DET the requires that this set be a singleton—thus we get Bumford’s absolute reading saying that there is exactly one hat, with exactly one rabbit in it.

The relative reading (corresponding to the (RR)-structure) comes in two variants: Champollion and Sauerland’s reading (Champollion and Sauerland 2011) and Bumford’s variant (Bumford 2017). Under our analysis, the head nominal rabbit undergoes a ‘sortal-to-relational’ shift and is modeled accordingly as the dependent type:

$$\begin{aligned} h:H \vdash R(h): \textsf {Type}, \end{aligned}$$

and extends the context by adding a variable r of type R(h):

$$\begin{aligned} h:H, r:R(h). \end{aligned}$$

The complex DP the rabbit in the hat is interpreted as the complex quantifier living on $\Vert \varSigma _{h:H} R(h)\Vert$. Simply combining this analysis with our semantic clause for the will not deliver the desired reading (in either of its variants):

$$\begin{aligned}&\Vert the_{h:H} the_{r: R(h)}\Vert = \{X \subseteq \Vert \varSigma _{h:H} R(h)\Vert : \{a \in \Vert H\Vert :\{b \in \Vert R\Vert (a): b \in X \}\\&\qquad \in \Vert the\Vert (\Vert R\Vert (a))\}\in \Vert the\Vert (\Vert H\Vert )\}. \end{aligned}$$

The above formula imposes a restriction that there be exactly one hat and exactly one rabbit such that this rabbit is in this hat—thus the rabbit in the hat cannot be used felicitously in the context with multiple salient hats.

A possible way to obtain Champollion and Sauerland’s reading would be to postulate that the is ambiguous between a presuppositional analysis (the) and a quantificational analysis (the’):

$$\begin{aligned} \Vert the'\Vert (\Vert X\Vert ) = \{Y\subseteq \Vert X\Vert : \overline{\Vert Y\Vert } = 1 \}, \end{aligned}$$

and give the following analysis to the whole DP the rabbit in the hat:

$$\begin{aligned}&\Vert the'_{h:H} the_{r: R(h)}\Vert \\&\quad = \{X \subseteq \Vert \varSigma _{h:H} R(h)\Vert : \{a \in \Vert H\Vert :\{b \in \Vert R\Vert (a): b \in X \} \\&\qquad \in \Vert the\Vert (\Vert R\Vert (a))\}\in \Vert the'\Vert (\Vert H\Vert )\}. \end{aligned}$$

The above formula imposes Champollion and Sauerland’s restriction that the number of hats that contain exactly one rabbit is exactly one—thus the rabbit in the hat can be used successfully in the context with multiple salient hats. The way to obtain Bumford’s reading would be to combine the definite determiner ‘unselectively’ with the type $\varSigma _{h:H} R(h)$ (consisting of pairs $\langle h, r\rangle$ such that h is of type H and r is of type R(h)), interpreted as the sum of fibers over elements in $\Vert H\Vert$

$$\begin{aligned} \Vert \varSigma _{h:H} R(h)\Vert \;= \; \bigsqcup _{a\in \Vert H\Vert } \Vert \pi _{R,h}\Vert ^{-1}(a). \end{aligned}$$

THE quantifies then over pairs (i.e., binds ‘unselectively’ all the variables in its scope):

$$\begin{aligned} \Vert { THE}\Vert (\Vert \varSigma _{h:H} R(h)\Vert ) \;= \; \left\{ \begin{array}{ll} \{\Vert \varSigma _{h:H} R(h)\Vert \} &{} \text{ if } \overline{\Vert \varSigma _{h:H} R(h)\Vert } = 1\\ \emptyset &{} \text{ otherwise, } \end{array} \right. \end{aligned}$$

and $\Vert { THE}\Vert (\Vert \varSigma _{h:H} R(h)\Vert$ denotes exactly one rabbit-hat pair, if there is a unique one, and the empty set, otherwise. Thus the above formula imposes Bumford’s ‘polyadic requirement’ that there be a single pair $\langle a, b\rangle$ such that a is a hat, b is a rabbit, and b is in a—the rabbit in the hat can be used felicitously in the context with multiple salient hats and multiple salient rabbits as long as there is exactly one pair of a rabbit and a hat such that the rabbit is in the hat.⁷ Our analysis allows us to derive the relative reading (in each of its variants) but it relies on additional amendments: presuppositional/quantificational ambiguity in the or the mechanism of unselective binding. We shall emphasize that these additional mechanisms are well motivated independently of Haddock definites.

Extending our analysis to PDs with definite possessors (e.g., the student of the linguist) would give an explanation of why the student of the linguist can be used successfully in contexts with multiple salient students and multiple salient linguists (as long as there is exactly one student-linguist pair). However, the controversial weak uses of PDs with definite possessors mentioned in the previous section cannot be explained using our analysis. Barker (2005) gives examples such as the side of the road which can be used felicitously in contexts in which the road in question has two equally silent sides (i.e., in contexts with multiple side-road pairs). For example, the sentence ‘It is safer to mount and dismount towards the side of the road, rather than in the middle of traffic’ is so constructed that the bicycle rider can be riding on either side of the road (left or right)—here, the speaker is perfectly aware that the road has two sides. We think that the problematic example mentioned may fall into a small group of idiosyncratic uses. In his paper, Barker discusses a well-known group of exceptions to uniqueness, e.g., ‘Could you please open the window?’ (uttered in a room with three equally silent windows), or ‘Please eat the apple (uttered when offering a bowl of apples). Barker’s claim is that such uses are idiosyncratic and have no implication for the treatment of systematic and productive uses. One clue that a use is idiosyncratic is that it does not tolerate modification, e.g., ‘Could you please open the tall window?’ is infelicitous in the context with two tall windows. Similarly, the examples of weak uses of PDs with definite possessors (adduced by Barker) may constitute a group of idiosyncratic exceptions to Haddock-type uniqueness, e.g., the side of the road (26,700,000 Google search results) also does not tolerate modification, as evidenced by 5 Google search results for the side of the long road or 4 results for the side of the beautiful road.

6 Preposition Puzzle

ILCs (e.g., a representative of every country) and PDs (e.g., the student of a linguist) are DPs which contain a QP which is selected by the preposition. This includes genitive of (connector to a relational noun) but also locative prepositions such as from or in. One puzzling difficulty for the existing accounts of ILCs is that some prepositions like with block inverse readings. A similar puzzle arises in connection with PDs—here, an even stronger claim has been made that ‘only the true genitive of systematically gives rise to weak interpretations’ (Barker 2005, p. 100). To illustrate the point, May and Bale (2005) give the example in (4):

• (4) Someone with every known skeleton key opened this door,

and Poesio (1994) gives the example in (5):

• (5) The student with a brown jacket.

Sentence in (4) can only mean that there is one individual who happens to have every known skeleton key and who opened the door; a use of the PD in (5) can only be felicitous in contexts in which there is a unique student with a brown jacket. By contrast, Haddock-type readings do not disappear in the presence of prepositions such as with. As discussed in Bumford’s (2017), HDs such as the table with the apple can be used successfully in contexts with multiple salient tables and multiple salient apples as long as there is exactly one pair of a table and an apple such that the table comes with the apple.

The solution to the preposition puzzle falls naturally out of the dependent type account proposed. First, both inverse and weak definite readings are unavailable for constructions (ILCs and PDs, respectively) with prepositions which induce dependencies corresponding to the surface ordering of the QPs. Note that in the case of prepositions like of and from, as in a representative of (from) every country, the ‘dependent component’ (representative) precedes in surface linear order the component on which it is dependent (country). Thus a representative of (from) every country introduces the dependency:

$$\begin{aligned} c:C, r:R(c), \end{aligned}$$

forcing the inverse ordering of the QPs $\forall _{c:C} \exists _{r:R(c)}$. By contrast, in the case of prepositions like with, as in a man with every key, the potentially ‘dependent component’ (key) follows the component on which it is dependent (man). Thus the only possible dependency to be introduced is:

$$\begin{aligned} m:M, k:K(m), \end{aligned}$$

one that corresponds to the surface ordering of the QPs $\exists _{m:M} \forall _{k:K(m)}$. By our global restriction on variables introduced in Sect. 2, the reading where $\forall$ outscopes $\exists$, $\forall _{k:K(m)}\exists _{m:M}$, is not available because the indexing variable m (in K(m)) is outside the scope of the binding occurrence of that variable. Thus, under the analysis proposed, the inverse interpretation is unavailable to the QP in the object position of with. Similarly PDs with the preposition of, e.g., the student of a linguist, introduce the dependency:

$$\begin{aligned} l:L, s:S(l), \end{aligned}$$

forcing the inverse ordering of the QPs $\exists _{l:L}, the_{s:S(l)}$. By contrast, in the case of prepositions like with, as in the student with a brown jacket, the potentially ‘dependent component’ (brown jacket) follows the component on which it is dependent (student). Thus the only possible dependency to be introduced is:

$$\begin{aligned} s:S, j:J(s), \end{aligned}$$

one that corresponds to the surface ordering of the QPs $the_{s:S} \exists _{j:J(s)}$. By our restriction on variables, the reading where $\exists$ outscopes the, $\exists _{j:J(s)}the_{s:S}$, is again not available because the indexing variable s (in J(s)) is outside the scope of the binding occurrence of that variable, and so the weak interpretation is unavailable to the QP in the object position of with.⁸ Second, by contrast to both inverse and weak definite readings, Haddock-type readings are insensitive to the prepositions used. This follows from the fact that the analyses proposed for such readings are not contingent on the dependencies in question. A HD like the rabbit in the hat or the table with the apple denotes a single pair (either a single rabbit-hat pair or a single table-apple pair), and the semantic analyses proposed can yield the pairs in question regardless of the dependencies involved.

7 Details of the Compositional Analysis

In this section, we shall sketch the remaining details of our compositional semantic analysis on the examples of sentences (6) and (7) involving ILCs:

• (6) A representative of every country is bald.

  $\forall _{c:C} \exists _{r:R(c)}\;\ Bald (r)$

• (7) A representative of every country missed a meeting.

  $\forall _{c:C} \exists _{r:R(c)} \;\ missed \;\ \exists _{m:M}$

Sentence in (6) is true iff

$$\begin{aligned} U^{-1}(\Vert Bald\Vert ) \in \Vert \forall _{c:C} \exists _{r:R(c)}\Vert \end{aligned}$$

i.e., if the set of bald representatives is in the denotation of the complex DP a representative of every country. The illustration below serves to provide an intuitive explanation of the formula:

Note that a person counts as a representative only in virtue of standing in a particular relationship with some country. Now each representative r has an underlying person U(r), in fact two representatives can have the same underlying person (if this person represents two countries). U stands for a function that forgets this part of the structure that relates people to countries and yields just people. Predicate Bald is defined over the type/set of people—by taking the inverse image of the set of bald people under the forgetting function U, $U^{-1}(\Vert Bald\Vert )$, we get the set of bald representatives. For sentence (6) to be true, the set of bald representatives must be in the denotation of the complex quantifier expression a representative of every country.

To derive the truth-conditions for (7), we propose to integrate our dependent type analysis into a continuation-passing framework (as in Barker 2002; Barker and Shan 2014; Grudzińska and Zawadowski 2017c). This will allow us to keep a non-movement (in situ) semantics for multi-quantifier sentences. In the continuation semantics, in order to combine with QPs a predicate needs to be lifted (‘continuized’), e.g., a predicate of type ${{\mathcal {P}}}(X) = X \rightarrow \mathbf{t}$ will be lifted to an expression of type ${{\mathcal {C}}}{{\mathcal {P}}}(X) = ((X \rightarrow \mathbf{t}) \rightarrow \mathbf{t}) \rightarrow \mathbf{t}$. A quantifier Q on type X is of type ${{\mathcal {C}}}(X) = (X \rightarrow \mathbf{t}) \rightarrow \mathbf{t}$—thus its meaning can be expressed only in continuized terms. For combining continuized predicates with QPs, we use two CPS composition rules (${{\mathcal {P}}}(X)=X\rightarrow \mathbf{t}$ and ${{\mathcal {C}}}(X)={{\mathcal {P}}}{{\mathcal {P}}}(X)$):

$$\begin{aligned} {\mathbf{CPS}^l}, {\mathbf{CPS}^r}: {{\mathcal {C}}}(X) \times {{\mathcal {C}}}(X\rightarrow Y) \longrightarrow {{\mathcal {C}}}(Y) \end{aligned}$$

For $M \in {{\mathcal {C}}}(X)$ and $R \in {{\mathcal {C}}}(X \longrightarrow Y)$,

$$\begin{aligned} {\mathbf{CPS}^l}(M, R) = \lambda c:{{\mathcal {P}}}(Y).M(\lambda x.R(\lambda f:X \longrightarrow Y. c(fx))) \end{aligned}$$

(argument-first)

$$\begin{aligned} {\mathbf{CPS}^r}(M, R) = \lambda c:{{\mathcal {P}}}(Y).R(\lambda f:X\longrightarrow Y.M(\lambda x. c(fx))) \end{aligned}$$

(function-first).

The two readings for the sentence (7) are derived as follows. The transitive predicate Miss is defined on $P(erson) \times M(eeting)$ and interpreted as the subset of $\Vert P(erson)\Vert \times \Vert M(eeting)\Vert$. It induces an obvious predicate Miss’ defined on $R(epresentatives) \times M(eeting)$ and interpreted as the subset of $\Vert \varSigma R\Vert \times \Vert M\Vert$, $(U \times 1)^{-1}(\Vert Miss\Vert )$. We now lift our predicate Miss’ to an expression of type ${{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R \times M)$, and combine the continuized predicate (of type ${{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R \times M)$) with the object QP a meeting (of type ${{\mathcal {C}}}(M)$) using either (left or right) of the two ${\mathbf{CPS}}$ transforms:

$$\begin{aligned} {\mathbf{CPS}^l}, {\mathbf{CPS}^r}: {{\mathcal {C}}}(M) \times {{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R \times M) \longrightarrow {{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R). \end{aligned}$$

For $A \in {{\mathcal {C}}}(M)$ and $P \in {{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R \times M)$,

$$\begin{aligned} {\mathbf{CPS}^l}(A,P) = \lambda c:{{\mathcal {C}}}(\varSigma R).A(\lambda m. P(\lambda p:{{\mathcal {P}}}(\varSigma R \times M). c(\lambda r. p(r,m)))). \end{aligned}$$

If $P = ev_{p'}, p' \in {{\mathcal {P}}}(\varSigma R \times M)$, then

$$\begin{aligned} {\mathbf{CPS}^l}(A, ev_{p'}) = \lambda c:{{\mathcal {C}}}(\varSigma R). A(\lambda m.c(\lambda r. p'(r,m))). \end{aligned}$$

The result thus obtained (G of type ${{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R)$) is then merged with the subject complex DP a representative of every country (of type ${{\mathcal {C}}}(\varSigma R)$), using ${\mathbf{CPS}}$ transforms again:

$$\begin{aligned} {\mathbf{CPS}^l}, {\mathbf{CPS}^r}: {{\mathcal {C}}}(\varSigma R) \times {{\mathcal {C}}}{{\mathcal {P}}}(\varSigma R) \longrightarrow {{\mathcal {C}}}(\mathbf{t}) \end{aligned}$$

Here depending on whether we use ${\mathbf{CPS}^l}$ or ${\mathbf{CPS}^r}$, we get either the surface ($\forall _{c:C} \exists _{r:R(c)} \exists _{m:M}$) or the inverse reading ($\exists _{m:M} \forall _{c:C} \exists _{r:R(c)}$) for the sentence in (7).

For $B\in {{\mathcal {C}}}(\varSigma R)$ and $G = \lambda c:{{\mathcal {C}}}(\varSigma R). A(\lambda m.c(\lambda r. p'(r,m)))$,

$$\begin{aligned} {\mathbf{CPS}^l}(B,G)= \lambda c':{{\mathcal {P}}}(\mathbf{t}).B(\lambda r: \varSigma R. G(\lambda g:{{\mathcal {P}}}(\varSigma R). c'(g, r))) \end{aligned}$$

application to the trivial continuation $c' = id_t$,

replacing G by $\lambda c:{{\mathcal {C}}}(\varSigma R). A(\lambda m.c(\lambda r. p'(r,m)))$

$$\begin{aligned} B(\lambda r: \varSigma R.\lambda c:{{\mathcal {C}}}(\varSigma R). A(\lambda m.c(\lambda r. p'(r,m)))(\lambda g:{{\mathcal {P}}}(\varSigma R).(g, r))) \end{aligned}$$

$\beta$-reduction

$$\begin{aligned} B(\lambda r: \varSigma R. A(\lambda m. (\lambda g:{{\mathcal {P}}}(\varSigma R).(g, r))(\lambda r'. p'(r',m)) \end{aligned}$$

$\beta$-reduction

$$\begin{aligned} B(\lambda r: \varSigma R. A(\lambda m. (\lambda r'. p'(r',m))r) \end{aligned}$$

$\beta$-reduction

$$\begin{aligned} B(\lambda r: \varSigma R. A(\lambda m. p'(r,m))) \end{aligned}$$

Calculations for ${\mathbf{CPS}^r}$ are similar and yield the inverse reading:

$$\begin{aligned} A(\lambda m. B(\lambda r: \varSigma R. p'(r,m))). \end{aligned}$$

One empirical constraint on a theory of inverse linking is the so-called Larson’s generalization (Larson 1985). Larson observed that QPs external to ILCs cannot take scope between the embedded and containing QPs. For example, sentence: ‘Two politicians spy on someone from every city’ can not be understood to mean that for every city c, there are two politicians who spy on someone from c—separate QP cannot take scope in between the two nested QPs: every city > two politicians > someone. Similarly, a meeting cannot take scope in between every country and a representative—the two interleaved interpretations are not possible for sentence (7). Note that under our analysis, the inseparability of the two nested QPs falls out immediately.

8 Conclusion

In this paper, we provided a unified dependent type account of the three problematic phenomena: inversely linked interpretations, weak definite readings in possessives and Haddock-type readings. We proposed that the three readings under consideration share the same underlying surface structure and we showed that the surface structure proposed can be interpreted compositionally and properly, using our semantic framework with dependent types. Furthermore, by introducing a restriction prohibiting free undeclared variables we were able to explain the puzzle of why both inversely linked interpretations and weak definite readings are blocked with certain prepositions (in contrast to Haddock-type readings). Our dependent type account is the first, as far as we are aware, to formally connect the three phenomena and to offer a principled solution to the preposition puzzle.