Deciphering the physical meaning of Gibbs’s maximum work equation

Abstract

J. Willard Gibbs derived the following equation to quantify the maximum work possible for a chemical reaction

${\text{Maximum work }} = \, - \Delta {\text{G}}_{{{\text{rxn}}}} = \, - \left( {\Delta {\text{H}}_{{{\text{rxn}}}} {-}{\text{ T}}\Delta {\text{S}}_{{{\text{rxn}}}} } \right) {\text{ constant T}},{\text{P}}$

∆H_rxn is the enthalpy change of reaction as measured in a reaction calorimeter and ∆G_rxn the change in Gibbs energy as measured, if feasible, in an electrochemical cell by the voltage across the two half-cells. To Gibbs, reaction spontaneity corresponds to negative values of ∆G_rxn. But what is T∆S_rxn, absolute temperature times the change in entropy? Gibbs stated that this term quantifies the heating/cooling required to maintain constant temperature in an electrochemical cell. Seeking a deeper explanation than this, one involving the behaviors of atoms and molecules that cause these thermodynamic phenomena, I employed an “atoms first” approach to decipher the physical underpinning of T∆S_rxn and, in so doing, developed the hypothesis that this term quantifies the change in “structural energy” of the system during a chemical reaction. This hypothesis now challenges me to similarly explain the physical underpinning of the Gibbs–Helmholtz equation

${\text{d}}\left( {\Delta {\text{G}}_{{{\text{rxn}}}} } \right)/{\text{dT}} = - \Delta {\text{S}}_{{{\text{rxn}}}} \left( {\text{constant P}} \right)$

While this equation illustrates a relationship between ∆G_rxn and ∆S_rxn, I don’t understand how this is so, especially since orbital electron energies that I hypothesize are responsible for ∆G_rxn are not directly involved in the entropy determination of atoms and molecules that are responsible for ∆S_rxn. I write this paper to both share my progress and also to seek help from any who can clarify this for me.

Introduction

At the end of a 2017 thermodynamics presentation by Dr. Raffaele Pisano that I was watching on YouTube, a grey-haired gentleman came to the microphone and said: “I have… a degree in physics. All of my friends went to engineering schools. We all agreed on one thing. And that is that thermodynamics was a black art. It was extremely difficult, abstract, and we swore over many glasses of beer we would never set foot in a room where the word thermodynamics was uttered again.” (Pisano 2017) Upon graduation, I could have sworn the same. As a chemical engineering student, I took both undergraduate and graduate level thermodynamics, did well, but never truly understood the subject. The phrase “black art” is apt.

Why today, 170 years after the founding of thermodynamics, do we continue to struggle to fully understand thermodynamics? I believe that the answer to this begins with a relevant quote often attributed to Albert Einstein: “If you can’t explain it simply, you don’t understand it well enough.” Generally speaking, to me, it’s clear that we don’t understand thermodynamics well enough, which naturally leads to the next question. Why not? What’s stopping us from understanding? I believe the reason is that we don’t fully understand the physical connections between the world of moving and interacting atoms and the world of thermodynamic phenomena and the equations used to characterize these phenomena. If we understood these connections better, we’d understand thermodynamics better and so be able to teach it better.

To close the gap, my guiding light is Richard Feynman.

All things are made of atoms – little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied. (Feynman et al. 1989a)

The bottom line is that we know much more about the atomic world today than the founders did in the mid to late 1800s. And it’s now time to use this knowledge to make thermodynamics more understandable. I refer to this approach as “atoms first” thermodynamics. Begin the syllabus with the atomic theory of matter as a foundation and then add thermodynamic terms, concepts, equations, and phenomena on top of this foundation, explaining clearly how each macro-concept connects with the underlying micro-content of the foundational base.

In this article I demonstrate how an “atoms first” approach to thermodynamics helps provide a physical explanation of a specific equation developed by J. Willard Gibbs to quantify the maximum external work that a chemical reaction, such as the combustion of coal, can generate. I was taught this equation in undergraduate thermodynamics and, to my embarrassment, graduated without understanding it. Long after college, frustrated by this situation and yet inspired to correct it, I employed an “atoms first” approach to decipher Gibbs’s equation and, in so doing, gained fresh insight into the meaning of his equation. In this article, I show how I arrived at this insight, share the resulting challenges from it regarding my inability to use it to physically understand the Gibbs–Helmholtz equation, and conclude with a request for help along with a recommendation on where we should go from here as regards the teaching of thermodynamics.

Historical background

Lost within Sadi Carnot's 1824 groundbreaking theoretical analysis of the steam engine (Carnot et al. 1986) was his overarching question: how much work can be generated from a bushel of coal? We continue to ask such questions today. While many use Carnot's ideas to determine the efficiency of a heat engine for a given amount of heat input, this is but a subset of the larger question: how much productive work can be generated from a given chemical reaction?

While different paths can transform resources like water and coal to productive work, in the end, no matter the path, the conservation of energy dictates that the maximum work possible is determined by the difference in energy between input and output. But what specific type of energy? By 1750 it was mechanical energy, especially as regards the water wheel. Water wheels captured the power embedded in falling water (potential energy) and flowing water (kinetic energy) to drive grain mills and power textile factories. Efficiency analysis, implicitly based on conservation of mechanical energy, became critical since the inputs—fall and flow of the water—were fixed. The maximum work possible (weight x change in vertical height) could not exceed the total change in kinetic plus potential energy of the moving and falling water, respectively.

Conducting comparable efficiency analyses on the steam engine, however, presented a problem. The input (coal) and output (work) had different units of measure. The ratio of output to input held no meaning. A new concept of energy was needed.

ΔH_rxn and the thermal theory of affinity

In the mid-1800s, technical analyses of the steam engine led to the discovery of two properties of matter, energy and entropy, and so laid the foundation for the science of thermodynamics—the transformation of heat to work. In this new way of thinking, the steam engine transforms chemical energy (the burning of coal) to mechanical energy (pressurized steam) that, in turn, generates productive work.

The conservation of energy dictated that the maximum work-energy produced by the steam engine couldn’t be greater than the chemical-energy consumed. Danish chemist Julius Thomsen in 1854 and separately French chemist Marcellin Berthelot in 1864 proposed that the chemical-energy available to generate work should be quantified by the value of ∆H_rxn (Kragh 1984). In other words, they proposed that ∆H_rxn quantifies the maximum work that can possibly be generated by a given chemical reaction. They further reasoned that when a reaction is exothermic (∆H_rxn < 0), it can generate work on its own, without added energy, and must therefore be spontaneous. Conversely, when a reaction is endothermic, energy is required to make it go and so can’t be spontaneous. This was their thinking at least.

Despite its lack of a theoretical underpinning, Thomsen and Berthelot’s thermal theory of affinity, as it became known, worked reasonably well for many processes. But not all of them. Sometimes all it takes is a single data point to eliminate a theory. In this case, the data point was the spontaneous endothermic reaction. According to Thomsen and Berthelot, it wasn’t supposed to happen, and yet it did.

The arrival of J. Willard Gibbs (1875–1878)

In considering this dilemma, J. Willard Gibbs realized that new properties of matter were needed, above and beyond those, such as internal energy (U) and entropy (S), created by Rudolf Clausius and others, in recognition of the fact that the real-world industrial processes were often conducted at constant temperature and pressure. To this end, Gibbs envisioned a system enclosed by a thermally conducting and flexible boundary (1875–1878) (Gibbs 1993). Such a system could be comprised of chemical reactants that upon reaction could generate external work (W_ext) while either absorbing or rejecting thermal energy to maintain constant temperature and either expanding or contracting to maintain constant pressure.

An energy balance of such a system reveals that the change in internal energy (U) of the system is equal to the pressure–volume (PdV) work done by the system, the thermal energy entering the system (Q), and the productive external work done by the system (W_ext).

• dU = δQ¹ – PdV – δW_ext.

Re-arranging this equation:

$$\delta {\text{W}}_{{{\text{ext}}}} = - {\text{dU }} - {\text{ PdV }} + \, \delta {\text{Q}}$$

By assuming constant temperature and pressure (H = enthalpy = U + PV; dH = dU + d(PV) = dU + PdV) and a reversible process (S = entropy; TdS = δQ),

$$\delta {\text{W}}_{{{\text{ext}}}} = - \left( {{\text{dH }}{-}{\text{ TdS}}} \right)$$

Gibbs then created a new composite property of matter, G, which later became known as Gibbs energy, such that the following equations could be written.

$${\text{G }} = {\text{ H }}{-}{\text{ TS}}$$

$$\delta {\text{W}}_{{{\text{ext}}}} = \, - {\text{dG }} = \, - \left( {{\text{dH }}{-}{\text{ TdS}}} \right) \left( {\text{constant temperature and pressure}} \right)$$

Finally, by assuming complete reaction, Gibbs quantified the maximum amount of external work as the change in Gibbs energy between reactants and products.

$${\text{Maximum work }} = {\text{ W}}_{{{\text{ext}}}} = \, - \Delta {\text{G}}_{{{\text{rxn}}}} = \, - \left( {\Delta {\text{H}}_{{{\text{rxn}}}} {-}{\text{ T}}\Delta {\text{S}}_{{{\text{rxn}}}} } \right) \, \left( {\text{constant temperature and pressure}} \right)$$

(1)

Gibbs’s work showed that it is ∆G_rxn and not ∆H_rxn that determines reaction spontaneity. For a reaction to generate positive work (W_ext > 0), the change in Gibbs energy must be negative (∆G_rxn < 0). This new theory explained that an endothermic reaction (∆H_rxn > 0) could indeed be spontaneous so long as T∆S_rxn > ∆H_rxn.

Unfortunately, while Gibbs’ maximum work equation successfully replaced the Thomsen-Berthelot thermal theory of affinity, it arrived absent a physical explanation.² How should one interpret this equation based on the microscopic world of moving and interacting atoms? The answer became clear, inadvertently so, when Gibbs turned his theoretical eyes toward the electrochemical cell.

Gibbs turns his thermodynamics toward the electrochemical cell

As I recount in Block by Block, (Hanlon 2022) the electric motor arrived as the result of a rapid sequence of historical milestones, starting with Alessandro Volta’s (1745–1827) invention of the battery in 1800, Hans Christian Ørsted’s (1777–1851) and André-Marie Ampère’s (1775–1836) separate works in 1819–1820 showing that electricity and magnetism interact with each other, and then Michael Faraday’s (1791–1867) invention of the electric motor in 1821, when he used magnets to demonstrate that electricity could produce motion and motion could produce electricity.

The arrival of the electric motor created much excitement throughout Europe and the United States as many thought that it offered improved performance over steam. Some even thought that “perpetual motion” lay hidden deep within the electro-magnetic device, prodded by Moritz Jacobi’s writings in 1835 that suggested the availability of near-infinite power from such a device. It was the self-educated Faraday who showed the fallacy of this thinking by demonstrating that the flow of electricity is accompanied by chemical change, e.g., the depletion of reactant chemicals zinc and copper from their respective electrodes and the accumulation of product chemicals zinc oxide on the copper electrodes and copper on the zinc electrodes.

Faraday’s studies demonstrated that chemical energy can be transformed to electrical energy, which can then drive a motor to lift a weight and generate productive work. This naturally led to the question, how much work can a chemical reaction generate in an electrochemical cell?

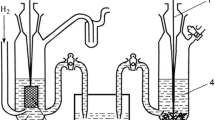
As very well summarized by Wilhelm Ostwald in his two-volume history of electrochemistry (Ostwald 1980), early researchers such as Pierre Antoine Favre and Johann T. Silbermann, François-Marie Raoult, and Hans Max Jahn, sought to answer this question by comparing the thermal effect of operating a given reaction on its own in a calorimeter against the thermal effect of operating the same reaction in the electrochemical cell (reversibly by using an external voltage source to counter the cell’s generated voltage) to generate electricity, which they converted to heat by sending the electricity through a very large resistor. These thermochemists discovered that the quantity of heat generated by the reaction (∆H_rxn) was not the same as that generated externally by the electricity. In other words, using today’s understanding of energy, their energy balances didn’t close, and the reason was that no one was paying attention to the thermal effects happening inside the electrochemical cell itself. This problem was resolved when these researchers placed the cell into a constant-temperature bath calorimeter and discovered additional heat effects that they then used to close the energy balance as summarized here:

$$\begin{aligned} {\text{Energy generated by the reaction itself }}\left( {\Delta {\text{H}}_{{{\text{rxn}}}} ;{\text{ calorimeter}}} \right)\, = & & \,{\text{energy generated external to the electrochemical cell}}\, \\ \qquad + \,{\text{energy exchanged between reaction cell and constant temperature bath}} \\ \end{aligned}$$

Citing selections from this work and in reference to Eq. (1), Gibbs³ concluded that the voltage established in an electrochemical cell is directly proportional to the maximum external work and is quantified by the term, − ∆G_rxn, and that the heating/cooling requirement to maintain the reaction system at constant temperature and pressure is quantified by his term, T∆S_rxn.

In 1882 Hermann von Helmholtz wrote of his own theoretical analysis of the electrochemical cell (Helmholtz 1882),

It has long been known that there are chemical processes which occur spontaneously and proceed without external force, and in which cold is produced. Of these processes the customary theoretical treatment [here referring to the Thomsen-Berthelot theory] can give no satisfactory account. A distinction must be made between the parts of their forces of affinity capable of free transformation into other forms of work, and the parts producible only as heat. In what follows I shall, for the sake of brevity, distinguish these two parts of the energy as the “free” and the “bound” energy. Spontaneous Process can take place only in such a direction as to cause diminution of free energy.

It was Helmholtz who gave us the concept of “free energy.” He and others realized that ∆H_rxn cannot be 100% transformed into external work (W_ext). Only the “free energy” (∆G_rxn) can be so transformed, while the remaining “bound” energy (T∆S_rxn) cannot.⁴

In the nineteen pages of his 3rd paper devoted to the thermodynamic theory of electrochemical cells, Gibbs highlighted the importance of the heating/cooling requirements to maintain isothermal conditions by stating such requirements are “frequently neglected”⁵ in the analysis of these cells. He argued that such effects should be captured as the value of T∆S, here making very effective use of Rudolf Clausius’s entropy (dS = dQ/T for a reversible process), and that the resulting equation could be used to quantify equilibrium conditions of a “perfect electro-chemical apparatus” for which the voltage difference between the two electrodes is perfectly countered by an external voltage such that the current is negligible and easily reversed.

Ultimately, Gibbs’s work with electrochemistry highlighted the need to account for entropy effects when calculating the maximum work potential of a chemical reaction. As an historical aside, in 1887 he shared this understanding⁶ in two famed letters to Sir Oliver Lodge, Secretary of the Electrolysis Committee of the British Association for the Advancement of Science. This theoretical contribution “profoundly affected the development of physical chemistry [and was] a potent factor in raising the industrial processes of [electrochemistry] from the realm of empiricism to that of an art governed by law, and thus [helped enable] the expansion of the electrochemical industry to its present vast proportions.”⁷

My interpretation of Gibbs’s maximum work equation

Table 1 is my attempt to seek a physical understanding of the terms in Gibbs’s maximum work Eq. (1). In the first column, I propose the physical/chemical changes that can cause thermal effects during a chemical reaction at constant T,P, and then compare these again Gibbs’s terms.

Table 1 My hypotheses connecting physical mechanism to the terms in Gibbs’s maximum work equation [1]

The entropy values involved in ∆S_rxn are based on the absolute entropies of the reactants and of the products. These values take into account both heat capacity and volume. Thus, to me, these values align with (2), (3), and (4) in the first column above. These values do not align with (1).

If this so, then ∆G_rxn must align with (1), as this is the only effect remaining. Hence my thought that ∆G_rxn quantifies the net change in orbital electron energies (and the associated voltage in an electrochemical cell) and it is this quantification that determines whether or not a reaction is spontaneous.

In sum, the value of ∆H_rxn as measured in a constant temperature reaction calorimeter is comprised of two energy effects, ∆Grxn and T∆Srxn. The electrochemical cell inadvertently and fortuitously (for our understanding) separates these two thermal effects as made clear here:

$$\Delta {\text{H}}_{{{\text{rxn}}}} = \Delta {\text{G}}_{{{\text{rxn}}}} + {\text{T}}\Delta {\text{S}}_{{{\text{rxn}}}}$$

My further interpretation: T∆S_rxn quantifies the change in “structural energy” of the system

The entropy of a given system quantifies the sum of the thermal energy differentials divided by the temperature of each differential from absolute zero to a given temperature, S = ∫ δQ/T, and inherently assumes that S = 0 at T = 0. δQ encompasses not only the thermal energy required to put the particles in motion but also the energy required to drive them apart from each other. T∆S_rxn thus quantifies the difference in energies required to establish each reactant and product system, the system being here defined by the atomic location and momentum of each atom, which are the two sources of entropy in Boltzmann’s statistical mechanics.

Regarding signs,

T∆S < 0

This means that thermal energy is generated in the electrochemical cell in going from reactants to products and so must be reversibly removed by the constant temperature bath, thereby representing a decrease in system entropy.

T∆S > 0

This means that a cooling effect happens in going from reactants to products. Thermal energy must be reversibly added, thereby representing an increase in system entropy.

Thus, in effect, the TS term, in a way, quantifies the energy contained in the structure of the system itself. It’s “bound” in the system, as Helmholtz would say but perhaps not for the same physics-based reasoning I just went through here. The change in thermal energy associated with the change in “structural energy” as quantified by T∆S_rxn is, per Gibbs, an actual heat effect as manifested by the heating/cooling requirement to maintain the reaction system at constant temperature and pressure. As such, it is a component of ∆H_rxn that cannot be used to do useful work.

Testing the validity of Eq. (1)

Testing the preceding interpretation of Eq. (1) requires the following: (1) the heating/cooling effect in an electrochemical cell needs to be quantified, and (2) absolute entropy values for both reactants and products need to be separately determined. Only in this way can (2) be compared against (1).

The historical challenge of (1) was that not many researchers actually quantified this value. The challenge of (2) and the reason why Gibbs himself didn’t perform this calculation is that the low-temperature technology wasn’t yet available to experimentally quantify absolute entropy values. Additionally, Walter Nernst’s 3rd law of thermodynamics, as modified by Max Planck (Nernst 1969), wouldn’t be stated until 1911: the entropy of pure crystalline molecules equals zero at absolute zero. The required data for (1) and (2) became available in the early 1900s.

A good data set I found was provided by Dodge in his 1944 thermodynamics book (Dodge 1944).The data, given without reference, are as follows:

$${\text{Hg }}\left( {\text{l}} \right) + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ Cl}}_{{2}} \left( {\text{g}} \right) = {\text{HgCl }}\left( {\text{s}} \right)$$

• ∆H_rxn =  − 31,300 cal per mole of HgCl formed (as measured in a constant T, P calorimeter)

• T = 25 °C (constant)

• W_E = 25,140 g.-cal per g.-mole (electrical work quantified by converting the electromotive force generated by the cell)

Unfortunately, the thermal energy exchange with the constant temperature bath was not directly measured but was instead calculated by assuming conservation of energy. Plugging these numbers into Eq. (1)

$${25},{14}0 = {31},{3}00 + {\text{T}}\Delta {\text{S}}_{{{\text{rxn}}}}$$

Thus,

$$\Delta {\text{S}}_{{{\text{rxn}}}} = - {6},{16}0/\left( {{25} + {273}} \right) \, = - {2}0.{67} {\text{cal}}/{\text{K}}$$

NIST tabulates absolute entropy values exist for the reactants and products in this reaction:

• Hg (l) = 75.9 J/mol*K⁸

• Cl₂ (g) = 223 J/mol*K⁹

• Hg₂Cl₂ (s) = 192.5 J/mol*K¹⁰ (I assume here that Dodge’s formula HgCl was later changed to Hg₂Cl₂ although I don’t have a reference for this. The value of ∆H_rxn for formation of Hg₂Cl₂ is listed in NIST as − 265 kJ/mol which translates into − 31,668 cal per mole of HgCl, comparable to Dodge’s value of − 31,300. Thus, I assume Dodge and NIST are referring to the same molecule.)

Calculating the value of ∆S_rxn based on NIST’s absolute values:

$$\Delta {\text{S}}_{{{\text{rxn}}}} = \, \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \, \left( {{192}.{5}} \right) - {75}.{9} - \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \, \left( {{223}} \right) = - {91}.{\text{15 J}}/{\text{mol}}*{\text{K}} = - {21}.{\text{78 calories per mole of HgCl }}\left( {\text{s}} \right){\text{ formed}}$$

Dodge’s value calculated from electrochemical experimental data of − 20.67 compares reasonably well against the value calculated from NIST’s absolute values of − 21.78.

Lewis and Gibson performed similar calculations (Lewis and Gibson 1917) to validate Eq. (1) by determining the atomic entropy of chlorine gas. They stated that the entropy based on the electrochemical cell data is reasonably close to the entropy based on direct measurement.

Given my interpretations, I don’t understand the Gibbs–Helmholtz equation

Table 1 is a hypothesis. It felt right when I made it and the above data help validate it. And yet I have since been challenged by a consequence of the hypothesis that I can’t explain. It has to do with the Gibbs–Helmholtz equation.

Differentiate Gibbs’s equation

$${\text{G}} = {\text{H}} - {\text{TS}}$$

$${\text{dG}} = {\text{dH }}{-}{\text{ TdS }}{-}{\text{ SdT }} = {\text{ dU }} + {\text{ PdV }} + {\text{ VdP }}{-}{\text{ TdS }}{-}{\text{ SdT}}$$

We know that for a system at equilibrium

$${\text{dU}} = {\text{TdS }}{-}{\text{ PdV}}$$

Thus,

$${\text{dG}} = {\text{VdP }}{-}{\text{ SdT}}$$

Assuming constant pressure and re-arranging

$${\text{dG}}/{\text{dT}} = - {\text{S}} \left( {\text{constant P}} \right)$$

Now if you write this equation once for the reactants and once for the products and then subtract the former from the latter, you get the famed Gibbs–Helmholtz equation, one of the most useful equations in chemical equilibrium

$${\text{d}}\Delta {\text{G}}_{{{\text{rxn}}}} /{\text{dT}} = - \Delta {\text{S}}_{{{\text{rxn}}}}$$

(2)

Equation (2) was experimentally verified in 1922 by Gerke (Gerke 1922) by varying the temperature of an electrochemical cell and calculating ∆S_rxn based on the response of ∆G_rxn and then finding reasonable agreement between the resulting ∆S_rxn values and those calculated separately from absolute entropy values determined directly. Barieau (Barieau 1950) further validated Eq. (2) by showing the equation to be valid for any reversible galvanic cell so long as the cell reaction is accurately written.

If my hypothesis in Table 1 is correct, the Gibbs–Helmholtz equations suggests that there must then be an exact relationship between the energy difference between orbital electrons in (1) and the entropic thermal changes in (2), (3), and (4). I don’t understand why this must be so, especially since orbital electrons are not directly involved in the determination of absolute entropy values. I also don’t understand how reaction spontaneity is determined by (1) and not by the change in entropy of the reaction involved with (2), (3), and (4), which is what I had been taught.

So I now come to the main objective of this paper. I need help. If you have a physical understanding of the Gibbs–Helmholtz Eq. (2) at the level of moving and interacting atoms, could you please share it with me?

Concluding thoughts

The disconnect between the physical world and classical thermodynamics was by design. Classical thermodynamics’ founders, unsure of what the atomic world looked like, adhered to sound scientific principles and kept the two separate. The result was an exact science acclaimed by Einstein as “the only physical theory of universal content which I am convinced will never be overthrown.” (Klein 1967) The downside is that it is just this disconnect that makes thermodynamics a challenge to learn.

To many, thermodynamics occurs as an indecipherable black box. The opportunity in front of us is to open the box, see what’s going on inside, and then use this learning as the first step in the process to connect the physical world with the foundations of thermodynamics. Such an atoms-first approach will result in better teaching and better learning. The better students learn and understand the tool called thermodynamics, the more apt they’ll be able to pro-actively, creatively, and confidently use it to come up with better solutions to the problems they’ll face as professionals.

The challenge in front of us is to develop this curriculum. Most of the material is already out there in the pages of books and journals and in the minds of many. It needs to be assimilated into one single place. And some of the material, such as the discussion in this article regarding Gibbs’s maximum work equation and the Gibbs–Helmholtz equation, remain to be developed and validated. If students are to reach their full capabilities, we need to gather and, where needed, create this content. This is the task in front of us. This is a goal worth working toward.