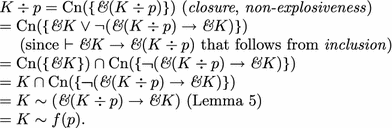Abstract
Specified meet contraction is the operation \(\div\) defined by the identity \(K \div p = K \,{\sim}\, f(p)\) where ∼ is full meet contraction and f is a sentential selector, a function from sentences to sentences. With suitable conditions on the sentential selector, specified meet contraction coincides with the partial meet contractions that yield a finite-based contraction outcome if the original belief set is finite-based. In terms of cognitive realism, specified meet contraction has an advantage over partial meet contraction in that the selection mechanism operates on sentences rather than on temporary infinite structures (remainders) that are cognitively inaccessible. Specified meet contraction provides a versatile framework in which other types of contraction, such as severe withdrawal and base-generated contraction, can be expressed with suitably chosen properties of the sentential selector.
Similar content being viewed by others
Notes
It can easily be shown that if K is not finite-based, then neither is any of its contraction outcomes by partial meet contraction. To see this, let \(\div\) be a partial meet contraction for a belief set K that is not finite-based, and let p ∈ K. Suppose for contradiction that \(K \div p\) is finite-based. Due to the recovery postulate that holds for partial meet contraction (Alchourrón et al. 1985), \(K = \hbox{Cn} ((K \div p) \cup \{p\}),\) so that K is finite-based, contrary to the assumption.
Omitting trivial cases, let \(p \in K \setminus \hbox{Cn} (\varnothing).\) Then success is equivalent with \(\nvdash\,\,(K\,{\sim}\,f(p)) \to p.\) Since K is finite-based, it follows from Lemma 5 that \(\nvdash\,\,(K\,{\sim}\,f(p)) \to p\) is equivalent with \(\nvdash\) (
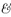 \(K\,\,\vee \neg f(p)\)) → p, where
\(K\,\,\vee \neg f(p)\)) → p, where 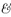 K is the conjunction of all elements of K. Since \(K \vdash p,\,\,\nvdash\) (
K is the conjunction of all elements of K. Since \(K \vdash p,\,\,\nvdash\) (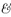 \(K\,\,\vee \neg f(p)\)) → p is equivalent with \(\nvdash\,\,p\,\,\vee f(p).\)
\(K\,\,\vee \neg f(p)\)) → p is equivalent with \(\nvdash\,\,p\,\,\vee f(p).\)
To see this, note that if \(K \div p \subseteq K \div q\) and \(q \notin \hbox{Cn} (\varnothing),\) then success yields \(q \notin K \div p.\)
References
Alchourrón, C., & Makinson, D. (1981). Hierarchies of regulation and their logic. In R. Hilpinen (Ed.), New Studies in Deontic Logic (pp. 125–148). D. Reider Publishing Company.
Alchourrón, C., & Makinson, D. (1982). On the logic of theory change: Contraction functions and their associated revision functions. Theoria, 48, 14–37.
Alchourrón, C., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. Journal of Symbolic Logic, 50, 510–530.
Fermé, E., & Rodriguez, R. (1998). A brief note about the Rott Contraction. Logic Journal of the IGPL, 8, 645–652.
Fuhrmann, A., & Hansson, S. O. (1994). A survey of multiple contraction. Journal of Logic, Language and Information, 3, 39–76.
Hansson, S. O. (1991). Belief contraction without recovery. Studia Logica, 50, 251–260.
Hansson, S. O. (1993). Theory contraction and base contraction unified. Journal of Symbolic Logic, 58, 602–625.
Hansson, S. O. (1994). Kernel contraction. Journal of Symbolic Logic, 59, 845–859.
Hansson, S. O. (1999). A textbook of belief dynamics. Theory change and database updating. Kluwer.
Makinson, D. (1987). On the status of the postulate of recovery in the logic of theory change. Journal of Philosophical Logic, 16, 383–394.
Rott, H. (1991). Two methods of construction contractions and revisions of knowledge systems. Journal of Philosophical Logic, 20, 149–173.
Rott, H. (1993). Belief contraction in the context of the general theory of rational choice. Journal of Symbolic Logic, 58, 1426–1450.
Rott, H., & Pagnucco, M. (1999). Severe withdrawal (and Recovery). Journal of Philosophical Logic, 28, 501–547.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proofs
Appendix: Proofs
Definition 5
Let X be finite-based. Then  X is a sentence such that \(\hbox{Cn} (X) = \hbox{Cn}\)({
X is a sentence such that \(\hbox{Cn} (X) = \hbox{Cn}\)({ X}).
X}).
Definition 6 (Fuhrmann and Hansson1994)
Lemma 1
If compactness and Zorn’s lemma hold, then: If\(X \subseteq A\)and\(X\,\,\nvdash\,\,p,\)then there is someX′ such that\(X \subseteq X^{\prime} \in A \perp p.\)
Proof of Lemma 1
See Alchourrón and Makinson 1981, p 129.
Lemma 2
If K is logically closed and\(X \in K \perp p,\)then X is logically closed.
Proof of Lemma 2
See Hansson 1999, p. 46.
Lemma 3
Let K be a logically closed set. If \(X \in K \perp p,\) then \(X \in K \perp q\) for all \(q \in K \setminus X.\)
Proof of Lemma 3
See Alchourrón et al. 1985, pp. 513–514 or Hansson 1999, pp. 48–49.
Lemma 4
Let K be a logically closed set and letp ∈ Kandq ∈ K. Then:
-
(1)
\(K \perp p \subseteq K \perp q\) if and only if \(\vdash q \to p.\)
-
(2)
\(K \perp (p \& q) = (K \perp p) \cup (K \perp q).\)
-
(3)
\(K \perp (p\,\,\vee q) = (K \perp p) \cap (K \perp q).\)
Proof of Lemma 4
Part 1: See Hansson 1999, p. 49. Part 2: See Alchourrón et al. 1985, p. 518 or Hansson 1999, p. 49. Part 3: See Rott 1993, p. 1434 or Hansson 1999 pp. 49–50.
Lemma 5
Let K be a logically closed set and ∼ the operator of full meet contraction for K. Then for all sentences\(p \in K:\)
Proof of Lemma 5
See Alchourrón and Makinson 1982, pp. 18–19 or Hansson 1999, pp. 125–126.
Lemma 6
-
(1)
If \(A \perp p \subseteq A \perp q,\) then \(A\,{\sim}\,q \subseteq A\,{\sim}\,p.\)
-
(2)
If K is finite-based and logically closed, \(p \in K,\)and\(K\,{\sim}\,q \subseteq K\,{\sim}\,p,\)then\(K \perp p \subseteq K \perp q.\)
Proof of Lemma 6
-
Part 1: Let \(A \perp p \subseteq A \perp q.\)
-
Case i, \(A \perp p = \varnothing:\) Then \(A\,{\sim}\,p = A,\) thus \(A\,{\sim}\,q \subseteq A\,{\sim}\,p.\)
-
Case ii, \(A \perp p \neq \varnothing:\) Then \(A \perp q \neq \varnothing,\) and we have \(A\,{\sim}\,p = \cap(A \perp p)\) and \(A\,{\sim}\,q = \cap (A \perp q).\) Let \(x \in A\,{\sim}\,q.\) Then \(x \in \cap (A \perp q),\) thus \(x \in \cap(A \perp p) = A\,{\sim}\,p.\)
-
-
Part 2: Let K be finite-based and let \(p \in K = \hbox{Cn} (K)\) and \(K\,{\sim}\,q \subseteq K\,{\sim}\,p.\)
-
Case i, \(p \in \hbox{Cn} (\varnothing):\) Then \(K \perp p = \varnothing,\) hence \(K \perp p \subseteq K \perp q.\)
-
Case ii, \(p \in K \setminus \hbox{Cn} (\varnothing):\) Then \(K\,{\sim}\,p \subset K,\) and it follows from \(K\,{\sim}\,q \subseteq K\,{\sim}\,p\) that \(q \in K \setminus \hbox{Cn} (\varnothing).\) We then have:
-
\(K\,{\sim}\,q \subseteq K\,{\sim}\,p\)
-
\(K \cap \hbox{Cn} (\{\neg q\}) \subseteq K \cap \hbox{Cn} (\{\neg p \})\) (Lemma 5)
-
\(\vdash\) (p →
 K) → (q →
K) → (q → K)
K) -
\(\vdash q \to p\) (since \(\vdash\)
 K → p)
K → p) -
\(K \perp p \subseteq K \perp q\) (Lemma 4:1)
-
Proof of Observation 1
-
Part 1: Let D be the set of atoms in the language that are not in p. (More precisely, d ∈ D iff there is some p′ such that \(\vdash p^{\prime} \leftrightarrow p\) and d is not a subformula in p′.) For each subset Z of D we can form the set \(Z^{+} = \{z\,\,\vee p \mid z \in Z\} \cup \{\neg z\,\,\vee p \mid z \in D \setminus Z\}.\) It follows from Lemma 1 (that uses Zorn’s lemma) that there is at least one W such that \(Z^+ \subseteq W \in K \perp p.\) This construction provides us with an infinite number of distinct elements of K ⊥ p.
-
Part 2: Let \(X \in K \perp p.\) Suppose for contradiction that X is finite-based. Then \(X = \hbox{Cn} (\{x\})\) for some sentence x. Let d be an atom not in x or p. (More precisely, let d be an atom such that there is some x′ with \(\vdash x \leftrightarrow x^{\prime}\) and some p′ with \(\vdash p \leftrightarrow p^{\prime}\) such that d is not a subformula either of x′ or of p′.)
We are first going to show that either \(\neg p \to d \in X\) or \(\neg p \to \neg d \in X.\) Let \(\neg p \to d \notin X.\) Then it follows from \(\neg p \to d \notin X \in K \perp p\) and \(\neg p \to d \in K\) (that follows from p ∈ K) that \(X \cup \{\neg p \to d\} \vdash p,\) thus \(X \vdash \neg p \to \neg d,\) thus due to Lemma 2, \(\neg p \to \neg d \in X.\) Contradiction.
Since p is a non-tautology, it follows from \(X \in K \perp p\) that \(X\,\,\nvdash\,\,p,\) thus \(X \cup \{\neg p\}\) is logically consistent. Since either \(\neg p \to d \in X\) or \(\neg p \to \neg d \in X,\) we have either \(X \cup \{\neg p\} \vdash d\) or \(X \cup \{\neg p\} \vdash \neg d,\) which is impossible due to the atomic structure assumed. This concludes the proof.
Proof of Observation 2
It follows from Lemma 5 that \(K \div p = K \sim f(p) = K \cap \hbox{Cn} (\{\neg f(p)\}) = \hbox{Cn} (\{f(p) \to \)
 K }).
K }).
Proof of Theorem 1
-
From Construction to Postulates:
-
Closure, inclusion: From the properties of full meet contraction.
-
Extensionality: Let \(\vdash p \leftrightarrow q.\) Due to C0, \(\vdash f(p) \leftrightarrow f(q).\) It follows from the properties of full meet contraction that \(K\,{\sim}\,f(p) = K\,{\sim}\,f(q).\)
-
Vacuity: Let If \(p \notin K.\) It follows from C1 that \(f(p) \notin K\) and from the properties of full meet contraction that \(K\,{\sim}\,f(p) = K.\)
-
Non-explosiveness: See Observation 2.
-
-
From Postulates to Construction:
-
Due to non-explosiveness,
 \((K \div p)\) is well-defined. We can therefore define f such that:
\((K \div p)\) is well-defined. We can therefore define f such that: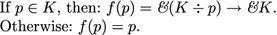 In order to verify the construction we need to show that the identity \(K \div p = K\,{\sim}\,f(p)\) holds and that C0 and C1 are satisfied.
In order to verify the construction we need to show that the identity \(K \div p = K\,{\sim}\,f(p)\) holds and that C0 and C1 are satisfied. -
The identity: In the case when \(p \notin K\) we have
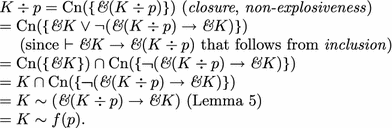
-
Property C0: If \(p \notin K,\) then this follows directly from the definition. For the case when p ∈ K, let \(\vdash p \leftrightarrow q.\) It follows from the extensionality of \(\div\) that \(K \div p = K \div q,\) and from this we obtain \(f(p) = f(q).\)
-
Property C1: For one direction, let p ∈ K. It follows from inclusion and the definition of f that f(p) ∈ K. For the other direction, let \(p \notin K.\) It follows from the definition of f that \(f(p) \notin K.\)
-
Proof of Theorem 2
-
From Construction to Postulates:
-
Part 1: Let \(p \in \hbox{Cn} (\varnothing).\) It follows from C2 that \(f(p) \in \hbox{Cn} (\varnothing),\) and from the properties of full meet contraction that \(K\,{\sim}\,f(p) = K.\)
-
Part 2: Let \(p \notin \hbox{Cn} (\varnothing).\)
-
Case i, p ∈ K. Then C3 yields:
-
\(\nvdash\,\,\neg p \to f(p)\)
-
\(p \notin \hbox{Cn} (\{\neg f(p)\})\)
-
\(p \notin K \cap \hbox{Cn} (\{\neg f(p)\})\)
-
\(p \notin K\,{\sim}\,f(p)\) (Lemma 5)
-
\(p \notin K \div p\)
-
-
Case ii, \(p \notin K:\) Then it follows from C1 that \(f(p) \notin K\) and from the properties of full meet contraction that \(K \div p = K\,{\sim}\,f(p) = K,\) thus \(p \notin K \div p.\)
-
-
Part 3:
-
Case i, p ∈ K. Then:
-
\(\vdash p \to f(p)\) (C4)
-
\(\vdash p \to f(p)\,\,\vee\)
 K
K
-
\(\vdash \neg f(p) \to (p \to\)
 K)
K) -
(p →
 K) \( \in \hbox{Cn} (\{\neg f(p)\})\)
K) \( \in \hbox{Cn} (\{\neg f(p)\})\)
-
(p →
 K) \(\in K \cap \hbox{Cn} (\{\neg f(p)\})\)
K) \(\in K \cap \hbox{Cn} (\{\neg f(p)\})\)
-
(p →
 K) ∈ K ∼ f(p) (Lemma 5, since f(p) ∈ K due to C1)
K) ∈ K ∼ f(p) (Lemma 5, since f(p) ∈ K due to C1) -
\(K \subseteq \hbox{Cn} ((K\,{\sim}\,f(p)) \cup \{p\})\)
-
\(K \subseteq \hbox{Cn} ((K \div p) \cup \{p\})\)
-
-
Case ii, \(p \notin K:\) Due to C1, \(f(p) \notin K,\) hence due to the properties of full meet contraction, \(K \div p = K,\) from which recovery follows.
-
-
-
From Postulates to Construction:
-
Part 1: Suppose that C2 does not hold. Then there is some p such that \(\vdash p\) and \(\nvdash\,\,f(p),\) hence \(\nvdash\)
 \((K \div p) \to\)
\((K \div p) \to\)
 K. But due to failure,
K. But due to failure, \((K \div p) =\)
\((K \div p) =\)  K. Contradiction.
K. Contradiction. -
Part 2: Let \(p \in K \setminus \hbox{Cn} (\varnothing).\) Then:
-
\(\nvdash\)
 \((K \div p) \to p\) (success)
\((K \div p) \to p\) (success) -
\(\nvdash\)
 \((K \div p) \to p\,\,\vee\)
\((K \div p) \to p\,\,\vee\) K (since p ∈ K)
K (since p ∈ K) -
\(\nvdash\,\,\neg p \to\) (
 \((K \div p) \to\)
\((K \div p) \to\)  K)
K) -
\(\nvdash\,\,\neg p \to f(p)\)
-
-
Part 3: Let p ∈ K. Then:
-
\(K \subseteq \hbox{Cn} ((K \div p) \cup {p})\) (recovery)
-
\(\vdash\) (
 \((K \div p) \& p\)) →
\((K \div p) \& p\)) →  K
K -
\(\vdash p \to\) (
 \((K \div p) \to\)
\((K \div p) \to\) K)
K) -
\(\vdash p \to f(p)\)
-
-
Proof of Observation 3
-
Part 1: Directly from the definition.
-
Part 2: It follows from \(\vdash p \to f(p)\) that \(\nvdash\,\,\neg p \to f(p)\) is equivalent with \(\nvdash\,\,f(p).\)
-
Part 3:
-
From C3 to C3r: Let C3 hold. For one direction of C3r, let \(\vdash p.\) It follows from C4 that \(\vdash f(p).\) For the other direction, let \(\vdash f(p).\) It follows from C3 that \(p \notin K \setminus \hbox{Cn} (\varnothing)\) and from C1 that p ∈ K, hence \(p \in \hbox{Cn} (\varnothing).\)
-
From C3r to C3: Let C3r hold and let \(p \in K \setminus \hbox{Cn} (\varnothing).\) It follows from C3r that \(f(p) \notin \hbox{Cn} (\varnothing)\) and then from C4 that \(\nvdash\,\,\neg p \to f(p).\)
-
Proof of Theorem 3
That (1) and (2) are equivalent follows directly from Theorems 1 and 2 and the standard axiomatic characterization of partial meet contraction with the six postulates closure, inclusion, vacuity, success, extensionality, and recovery. (Alchourrón et al. 1985). That (2) and (3) are equivalent follows directly from Observation 3, part 3.
Proof of Theorem 4
-
From Construction to Postulates:
-
Part 1:
-
Case i, p, q ∈ K: For symmetry reasons we can assume that \(\vdash f(p) \to f(q).\) We then have:
-
\(\vdash f(p) \to f(q)\)
-
\(K \perp f(q) \subseteq K \perp f(p)\) (Lemma 4:1 since \(f(p), f(q) \in K\) due to (C1))
-
\(K\,{\sim}\,f(p) \subseteq K\,{\sim}\,f(q)\) (Lemma 6).
-
\(K \div p \subseteq K \div q\)
-
-
Case ii, \(p \notin K\) or \(q \notin K:\) Then due to (C1) either \(K \div p = K\) or \(K \div q = K.\) The rest is trivial.
-
-
Part 2: Failure follows from C2 and Theorem 2. For weak hierarchy, let \(q \notin K \div p.\)
-
Case i, \(p \notin K \setminus \hbox{Cn} (\varnothing):\) Then it follows from C1, C2, and the properties of full meet contraction that \(K \div p = K.\) It then follows from \(q \notin K \div p = K,\) according to C1, that \(f(q) \notin K,\) hence \(K \div q = K,\) so that \(K \div q \not \subset K \div p.\)
-
Case ii, \(q \notin K \setminus \hbox{Cn} (\varnothing):\) Then it follows from C1, C2, and the properties of full meet contraction that \(K \div q = K.\) Since \(K \div p \subseteq K\) due to the properties of full meet contraction we have \(K \div q \not \subset K \div p.\)
-
Case iii, \(p, q \in K \setminus \hbox{Cn} (\varnothing):\) We then have:
-
\(q \notin K \div p\)
-
\(q \notin K\,{\sim}\,f(p)\)
-
\(q \notin K \cap \hbox{Cn} (\{\neg f(p)\})\) (Lemma 5)
-
\(q \notin \hbox{Cn} (\{\neg f(p)\})\) (since q ∈ K)
-
\(\nvdash\,\,\neg q \to f(p)\)
-
Either \(\nvdash\,\,f(q) \to f(p)\) or \(\vdash f(p) \to f(q)\) (C6)
-
Either \(K \perp f(p) \not \subseteq K \perp f(q)\) or \(K \perp f(q) \subseteq K \perp f(p)\) (Lemma 4:1)
-
Either \(K\,{\sim}\,f(q) \not \subseteq K\,{\sim}\,f(p)\) or \(K\,{\sim}\,f(p) \subseteq K\,{\sim}\,f(q)\) (Lemma 6)
-
\(K\,{\sim}\,f(q) \not \subset K\,{\sim}\,f(p)\)
-
\(K \div q \not \subset K \div p\)
-
-
-
Part 3: Failure follows from C2 and Theorem 2. For hierarchy, let \(q \notin K \div p.\)
-
Case i, \(p \notin K \setminus \hbox{Cn} (\varnothing):\) It follows from C1, C2, and the properties of full meet contraction that \(K \div p = K.\) Then \(q \notin K \div p\) yields \(q \notin K,\) and it follows from C1 that \(K \div q = K.\)
-
Case ii, \(q \notin K \setminus \hbox{Cn} (\varnothing):\) It follows from C1, C2, and the properties of full meet contraction that \(K \div q = K.\) Furthermore, \(K \div p \subseteq K\) follows from the properties of full meet contraction.
-
Case iii, \(p, q \in K \setminus \hbox{Cn} (\varnothing):\)
-
\(q \notin K \div p\)
-
\(K \cap \hbox{Cn} (\{\neg f(p)\})\,\,\nvdash\,\,q\) (Lemma 5)
-
\(\nvdash\)
 \(K\,\,\vee \neg f(p) \to q\)
\(K\,\,\vee \neg f(p) \to q\)
-
\(\nvdash\,\,\neg q \to f(p)\) (since
 \(K \vdash q\))
\(K \vdash q\)) -
\(\vdash f(p) \to f(q)\) (C7)
-
\(K \perp f(q) \subseteq K \perp f(p)\) (Lemma 4:1 since \(f(p), f(q) \in K\) due to C1)
-
\(K\,{\sim}\,f(p) \subseteq K\,{\sim}\,f(q)\) (Lemma 6)
-
\(K \div p \subseteq K \div q\)
-
-
-
-
From Postulates to Construction:
-
Part 1: Let p, q ∈ K. For symmetry reasons we may assume that \(K \div p \subseteq K \div q.\) Then we have \(\vdash \)
 \((K \div q) \to\)
\((K \div q) \to\)
 \((K \div p).\) It follows from inclusion (Theorem 1) that \(\vdash\)
\((K \div p).\) It follows from inclusion (Theorem 1) that \(\vdash\)
 K →
K → \((K \div p).\) From this it follows truthfunctionally that \(\vdash\) (
\((K \div p).\) From this it follows truthfunctionally that \(\vdash\) ( \((K \div p) \to\)
\((K \div p) \to\)
 K) → (
K) → ( \((K \div q) \to\)
\((K \div q) \to\)
 K), thus \(\vdash f(p) \to f(q),\) as desired.
K), thus \(\vdash f(p) \to f(q),\) as desired. -
Part 2: It follows from failure and Theorem 2 that C2 is satisfied. We are going to prove C6 in the following equivalent form:
-
(C6’) For all \(p, q \in K:\)
-
If \(\nvdash\,\,\neg p \to f(q)\) and \(\vdash f(p) \to f(q),\) then \(\vdash f(q) \to f(p).\)
Let \(\nvdash\,\,\neg p \to f(q)\) and \(\vdash f(p) \to f(q).\) It follows from \(\nvdash\,\,\neg p \to f(q),\) i.e. \(\nvdash\,\,\neg p \to ((K \div q) \to\)
 K) that \(\nvdash\)
K) that \(\nvdash\)
 \((K \div q) \to p,\) hence \(p \notin K \div q.\)
Weak hierarchy yields \(K \div p \not \subset K \div q.\) From \(\vdash f(p) \to f(q),\) i.e. \(\vdash\) (
\((K \div q) \to p,\) hence \(p \notin K \div q.\)
Weak hierarchy yields \(K \div p \not \subset K \div q.\) From \(\vdash f(p) \to f(q),\) i.e. \(\vdash\) ( \((K \div p) \to\)
\((K \div p) \to\)
 K) → (
K) → ( \((K \div q) \to\)
\((K \div q) \to\)
 K) and \(\vdash\)
K) and \(\vdash\)
 K →
K → \((K \div p)\) that follows from inclusion, we obtain \(\vdash\)
\((K \div p)\) that follows from inclusion, we obtain \(\vdash\)
 \((K \div q) \to\)
\((K \div q) \to\)
 \((K \div p),\) hence \(K \div p \subseteq K \div q.\) From this and \(K \div p \not \subset K \div q\) follows \(\vdash\)
\((K \div p),\) hence \(K \div p \subseteq K \div q.\) From this and \(K \div p \not \subset K \div q\) follows \(\vdash\)
 \((K \div p) \leftrightarrow\)
\((K \div p) \leftrightarrow\)
 \((K \div q).\) From this follows \(\vdash\) (
\((K \div q).\) From this follows \(\vdash\) ( \((K \div q) \to\)
\((K \div q) \to\)
 K) → (
K) → ( \((K \div p) \to\)
\((K \div p) \to\)
 K), i.e. \(\vdash f(q) \to f(p).\)
K), i.e. \(\vdash f(q) \to f(p).\)
-
-
Part 3: C2 follows from failure and Theorem 2. For C7, let \(p, q \in K\) and let \(\nvdash\,\,\neg q \to f(p),\) i.e. \(\nvdash\,\,\neg q \to\) (
 \((K \div p) \to\)
\((K \div p) \to\)
 K). It follows that \(\nvdash\)
K). It follows that \(\nvdash\)
 \((K \div p) \to q,\) hence \(q \notin K \div p,\) and hierarchy yields \(K \div p \subseteq K \div q.\) Then we have \(\vdash\)
\((K \div p) \to q,\) hence \(q \notin K \div p,\) and hierarchy yields \(K \div p \subseteq K \div q.\) Then we have \(\vdash\)
 \((K \div q) \to\)
\((K \div q) \to\)
 \((K \div p).\) It follows from inclusion that \(\vdash\)
\((K \div p).\) It follows from inclusion that \(\vdash\)
 K →
K →  \((K \div p).\) From this it follows truth-functionally that \(\vdash\)(
\((K \div p).\) From this it follows truth-functionally that \(\vdash\)( \((K \div p) \to\)
\((K \div p) \to\)
 K) → (
K) → ( \((K \div q) \to\)
\((K \div q) \to\)
 K), thus \(\vdash f(p) \to f(q),\) as desired.
K), thus \(\vdash f(p) \to f(q),\) as desired.
-
Proof of Observation 4
-
Part 1: Directly from the definition.
-
Part 2: From C5 and C6 to C7: Let p, q ∈ K and \(\nvdash\,\,\neg q \to f(p).\) It follows from C6 that either \(\vdash f(p) \to f(q)\) or \(\nvdash\,\,f(q) \to f(p),\) and then from C5 that \(\vdash f(p) \to f(q).\)
-
From C7 to C5: Let p, q ∈ K. If \(p \in \hbox{Cn} (\varnothing)\) then C2 yields \(\vdash f(p)\) and \(\vdash f(q) \to f(p)\) follows directly. The case when \(q \in \hbox{Cn} (\varnothing)\) is treated analogously.
In the principal case when \(p, q \in K \setminus \hbox{Cn} (\varnothing)\) we have \(p \&q \in K \setminus \hbox{Cn} (\varnothing)\) and C3 yields \(\nvdash\,\,\neg (p \& q) \to f(p \& q).\) Thus, either \(\nvdash\,\,\neg p \to f(p \& q)\) or \(\nvdash\,\,\neg q \to f(p \&q).\) In the former case, C7 yields \(\vdash f(p \& q) \to f(p).\) Since C3 also provides us with \(\nvdash\,\,\neg q \to f(q)\) we have \(\nvdash\,\,\neg (p \& q) \to f(q)\) and we can conclude from C7 that \(\vdash f(q) \to f(p \& q).\) This can be combined with \(\vdash f(p \& q) \to f(p)\) to obtain \(\vdash f(q) \to f(p).\) In the other case, \(\vdash f(p) \to f(q)\) can be proved in the same way.
-
From C7 to C6: Let \(p, q \in K,\,\, \vdash f(p) \to f(q)\) and \(\nvdash\,\,f(q) \to f(p).\) It follows by C7 from \(\nvdash\,\,f(q) \to f(p)\) that \(\vdash \neg p \to f(q).\)
-
Proof of Observation 5
Suppose to the contrary that f satisfies C3w, C4, and C5. Let the two non-tautologies in K be p and q. Since K is logically closed, \(p \leftrightarrow q \in K.\) Using C5, we can assume without loss of generality that \(\vdash f(p) \to f(q).\) There are two cases:
-
Case i, \(\vdash f(q) \to f(p \leftrightarrow q):\) It follows from this, \(\vdash f(p) \to f(q),\,\, \vdash p \to f(p),\) and \(\vdash q \to f(q)\) that \(\vdash p \to f(p \leftrightarrow q)\) and \(\vdash q \to f(p \leftrightarrow q).\) From this and \(\vdash (p \leftrightarrow q) \to f(p \leftrightarrow q)\) follows \(\vdash f(p \leftrightarrow q).\) Since p and q are non-equivalent, this contradicts C3w.
-
Case ii, \(\nvdash\,\,f(q) \to f(p \leftrightarrow q):\) Then due to C5, \(\vdash f(p \leftrightarrow q) \to f(q).\) From this, \(\vdash f(p) \to f(q),\,\, \vdash p \to f(p),\) and \(\vdash (p \leftrightarrow q) \to f(p \leftrightarrow q)\) it follows that \(\vdash p \to f(q)\) and \(\vdash (p \leftrightarrow q) \to f(q).\) From this and \(\vdash q \to f(q)\) it follows that \(\vdash f(q).\) Since q is not a tautology, this contradicts C3w.
Proof of Observation 6
Let q and r be the two non-equivalent non-tautologies in K. Since K is logically closed, \(q \leftrightarrow r \in K.\) Using alternative inclusion we can assume without loss of generality that \(K \div q \subseteq K \div r.\)
-
Case i, \(K \div r \subseteq K \div (q \leftrightarrow r):\) Then we also have \(K \div q \subseteq K \div (q \leftrightarrow r).\) Due to the weakened success postulate, there is some sentence s ∈ K such that \(s \notin K \div (q \leftrightarrow r).\) Due to recovery, \(K \div q \vdash q \to s, K \div r \vdash r \to s,\) and \(K \div (q \leftrightarrow r) \vdash (q \leftrightarrow r) \to s.\) It follows from this, \(K \div r \subseteq K \div (q \leftrightarrow r),\) and \(K \div q\subseteq K \div (q \leftrightarrow r)\) that \(K \div (q \leftrightarrow r) \vdash s,\) thus due to closure\(s \in K \div (q \leftrightarrow r),\) contrary to the assumption.
-
Case ii, \(K \div r \not \subseteq K \div (q \leftrightarrow r)\) : Then due to alternative inclusion, \(K \div (q \leftrightarrow r) \subseteq K \div r.\) Due to the weakened success postulate, there is some sentence s ∈ K such that \(s \notin K \div r.\) Due to recovery, \(K \div q \vdash q \to s,\,\, K \div r \vdash r \to s,\) and \(K \div (q \leftrightarrow r) \vdash (q \leftrightarrow r) \to s.\) It follows from this and \(K \div (q \leftrightarrow r) \subseteq K \div r\) and \(K \div q \subseteq K \div r\) that \(K \div r \vdash s,\) thus due to closure\(s \in K \div r,\) contrary to the assumption.
Proof of Theorem 5
-
From Construction to Postulates:
-
Part 1: Let \(K \div r \vdash p\) iff \(K \div r \vdash q\) for all r.
-
Case i, \(p \notin K\) : Then clearly \(q \notin K,\) and \(K \div p = K \div q\) follows from C1 and the properties of full meet contraction.
-
Case ii, p ∈ K:
-
For all \(r,\,\, K\,{\sim}\,f(r) \vdash p\) iff \(K\,{\sim}\,f(r) \vdash q\)
-
For all \(r,\,\, K \cap \hbox{Cn} (\{\neg f(r)\}) \vdash p\) iff \(K \cap \hbox{Cn} (\{\neg f(r)\}) \vdash q\) (Lemma 5)
-
For all r,
 \(K\,\,\vee \neg f(r) \vdash p\) iff
\(K\,\,\vee \neg f(r) \vdash p\) iff  \(K\,\,\vee \neg f(r) \vdash q\)
\(K\,\,\vee \neg f(r) \vdash q\)
-
For all \(r,\,\, \vdash \neg p \to f(r)\) iff \(\vdash \neg q \to f(r)\) (since
 \(K \vdash p\) and
\(K \vdash p\) and  \(K \vdash q\))
\(K \vdash q\)) -
\(\vdash f(p) \leftrightarrow f(q)\) (C8)
-
\(K\,{\sim}\,f(p) = K\,{\sim}\,f(q)\)
-
\(K \div p = K \div q\)
-
-
-
Part 2: Failure and success follow from C2, C3 and Theorem 2. Weak conservativity:
-
Case i, \(p \notin K \setminus \hbox{Cn} (\varnothing)\): It follows from C1, C2, and the properties of full meet contraction that \(K \div p = K\) and \(K \div q \subseteq K,\) thus \(K \div q \subseteq K \div p.\)
-
Case ii, \(p \in K \setminus \hbox{Cn} (\varnothing)\) and \(q \notin K \setminus \hbox{Cn} (\varnothing):\) If follows from C1, C2, and the properties of full meet contraction that \(K \div q = K.\) Let r = p. Then \(f(r) = f(p).\) Since \(p \in K \setminus \hbox{Cn} (\varnothing)\) it follows from C3 and Theorem 2 that \(K \div r\,\,\nvdash\,\,p.\) It follows from p ∈ K and \(K \div q = K\) that \(K \div r \cup K \div q \vdash p.\)
-
Case iii, \(p, q \in K \setminus \hbox{Cn} (\varnothing):\) Let \(K \div q \not \subseteq K \div p,\) Then:
-
\(K\,{\sim}\,f(q) \not \subseteq K\,{\sim}\,f(p)\)
-
\(K \perp f(p) \not \subseteq K \perp f(q)\) (Lemma 6)
-
\(\nvdash\,\,f(q) \to f(p)\) (Lemma 4:1 and C1)
-
There is some r such that \(\nvdash\,\,\neg p \to f(r)\) and \(\vdash \neg p \to f(q)\,\,\vee f(r)\) (C9)
-
From \(\nvdash\,\,\neg p \to f(r)\) we obtain:
-
\(p \notin \hbox{Cn} (\{\neg f(r)\})\)
-
\(p \notin K \cap \hbox{Cn} (\{\neg f(r)\})\)
-
\(p \notin K\,{\sim}\,f(r) \) (Lemma 5)
-
\(K \div r\,\,\nvdash\,\,p.\)
-
From \(\vdash \neg p \to f(q)\,\,\vee f(r)\) we obtain:
-
\(\neg f(q) \& \neg f(r) \vdash p\)
-
 \(K\,\,\vee (\neg f(q) \& \neg f(r)) \vdash p\) (since C1 yields p ∈ K)
\(K\,\,\vee (\neg f(q) \& \neg f(r)) \vdash p\) (since C1 yields p ∈ K) -
(
 \(K\,\,\vee \neg f(q))\) & (
\(K\,\,\vee \neg f(q))\) & ( \(K\,\,\vee \neg f(r)) \vdash p\)
\(K\,\,\vee \neg f(r)) \vdash p\)
-
\((K \cap \hbox{Cn} (\{\neg f(q)\})) \cup (K \cap \hbox{Cn} (\{\neg f(r)\})) \vdash p\)
-
\((K\,{\sim}\,f(q)) \cup (K\,{\sim}\,f(r)) \vdash p\) (Lemma 5)
-
\((K \div q) \cup (K \div r) \vdash p\)
-
-
-
Part 3: This proof is based on the proof of part 2. Case i is similar. In cases ii and iii we only have to add a proof that \(K \div p \subseteq K \div r.\) In case ii this is trivial. In case iii we have:
-
\(\vdash f(p) \to f(r)\) (C10)
-
\(K \perp f(r) \subseteq K \perp f(p)\) (Lemma 4:1 and C1)
-
\(K\,{\sim}\,f(p) \subseteq K\,{\sim}\,f(r)\) (Lemma 6)
-
\(K \div p \subseteq K \div r\)
-
-
-
From Postulates to Construction:
-
Part 1: Let p, q ∈ K and assume that for all \(r,\,\, \vdash \neg p \to f(r)\) iff \(\vdash \neg q \to f(r).\) Then equivalently:
-
For all \(r:\,\, \vdash \neg p \to\) (
 \((K \div r) \to\)
\((K \div r) \to\)
 K) iff \(\vdash \neg q \to\) (
K) iff \(\vdash \neg q \to\) ( \((K \div r) \to\)
\((K \div r) \to\)
 K)
K) -
For all r:
 \((K \div r) \vdash p\,\,\vee\)
\((K \div r) \vdash p\,\,\vee\)
 K iff
K iff  \((K \div r) \vdash q\,\,\vee\)
\((K \div r) \vdash q\,\,\vee\)
 K
K
-
For all \(r:\,\, p \in K \div r\) iff \(q \in K \div r\) (since \(p, q \in K\))
-
\(K \div p = K \div q\) (symmetry)
-
\(\vdash\) (
 \((K \div p) \to\)
\((K \div p) \to\) K) \(\leftrightarrow\) (
K) \(\leftrightarrow\) ( \((K \div q) \to\)
\((K \div q) \to\) K)
K) -
\(\vdash f(p) \leftrightarrow f(q)\)
-
-
Part 2: C2 and C3 follow from failure, success, and Theorem 2. It remains to show that C9 holds. Let \(p, q \in K\) and let \(\nvdash\,\,f(q) \to f(p),\) i.e. \(\nvdash\) (
 \((K \div q) \to\)
\((K \div q) \to\)
 K) → (
K) → ( \((K \div p) \to\)
\((K \div p) \to\)
 K). Since \(\vdash\)
K). Since \(\vdash\)
 K →
K →  \((K \div q)\) (due to inclusion) this is equivalent with \(\nvdash\)
\((K \div q)\) (due to inclusion) this is equivalent with \(\nvdash\)
 \((K \div p) \to\)
\((K \div p) \to\)
 \((K \div q),\) hence \(K \div q \not \subseteq K \div p.\) It follows from weak conservativity that there is some r such that \(K \div r\,\,\nvdash\,\,p\) and \(K \div r \cup K \div q \vdash p.\)
\((K \div q),\) hence \(K \div q \not \subseteq K \div p.\) It follows from weak conservativity that there is some r such that \(K \div r\,\,\nvdash\,\,p\) and \(K \div r \cup K \div q \vdash p.\)
-
From \(K \div r\,\,\nvdash\,\,p\) it follows that
-
\(\nvdash\)
 \((K \div r) \to p\)
\((K \div r) \to p\)
-
\(\nvdash\)
 \((K \div r) \to p\,\,\vee\)
\((K \div r) \to p\,\,\vee\) K (since p ∈ K)
K (since p ∈ K) -
\(\nvdash\,\,\neg p \to\) (
 \((K \div r) \to\)
\((K \div r) \to\) K)
K) -
\(\nvdash\,\,\neg p \to f(r)\)
-
-
From \(K \div r \cup K \div q \vdash p\) it follows that
-
 \((K \div r)\) &
\((K \div r)\) & \((K \div q) \vdash p\)
\((K \div q) \vdash p\) -
\(\vdash \neg p \to\)(
 \((K \div q) \to\)
\((K \div q) \to\) K) ∨ (
K) ∨ ( \((K \div r) \to\)
\((K \div r) \to\) K)
K) -
\(\vdash \neg p \to f(q)\,\,\vee f(r)\)
-
-
-
Part 3: This proof is based on the proof of part 2. It remains to strengthen C9 to C10 by showing that \(\vdash f(p) \to f(r).\) This is done as follows:
-
\(K \div p \subseteq K \div r\) (conservativity)
-
\(K\,{\sim}\,f(p) \subseteq K\,{\sim}\,f(r)\)
-
\(K \perp f(r) \subseteq K \perp f(p)\)(Lemma 6. It follows from p ∈ K and \(K\,{\sim}\,f(r)\,\,\nvdash\,\,p\) that f(r) ∈ K.)
-
\(\vdash f(p) \to f(r)\) (Lemma 4:1, f(p) ∈ K follows from C1)
-
-
Proof of Observation 7
-
Part 1: Directly from the definition.
-
Part 2: Let p, q ∈ K.
-
Case i, \(p \in \hbox{Cn} (\varnothing):\) Then it follows from C2 that \(\vdash f(p).\) We will prove the converse form of C8. Let \(\nvdash\,\,f(p) \leftrightarrow f(q).\) Then \(\nvdash\,\,f(q)\) and C2 yields \(\nvdash\,\,q.\) It follows from C3 that \(\nvdash\,\,\neg q \to f(q).\) It follows from \(p \in \hbox{Cn} (\varnothing)\) that \(\vdash \neg p \to f(q).\) Thus there is some r, namely r = q, such that \(\vdash \neg p \to f(r)\) and \(\nvdash\,\,\neg q \to f(r).\)
-
Case ii, \(q \in \hbox{Cn} (\varnothing):\) Symmetrical with the previous case.
-
Case iii, \(p, q \in K \setminus \hbox{Cn} (\varnothing):\) We will prove the converse form of C8. Let \(\nvdash\,\,f(p) \leftrightarrow f(q).\) Due to C5 we can assume without loss of generality that \(\vdash f(p) \to f(q)\) and \(\nvdash\,\,f(q) \to f(p).\) It follows directly from C6 that \(\vdash \neg p \to f(q).\) It follows from C3 that \(\nvdash\,\,\neg q \to f(q).\) Hence it is not the case that \(\vdash \neg p \to f(q)\) iff \(\vdash \neg q \to f(q).\)
-
-
Part 3: Let p, q ∈ K and \(\nvdash\,\,f(q) \to f(p).\) Then \(f(p) \notin \hbox{Cn} (\varnothing).\) It follows from C5 that \(\vdash f(p) \to f(q)\) and then from C6 that \(\vdash \neg p \to f(q).\) Due to C3, \(\nvdash\,\,\neg p \to f(p).\) Let r = p. We then have \(\vdash f(p) \to f(r),\,\, \nvdash\,\,\neg p \to f(r),\) and \(\vdash \neg p \to f(q)\,\,\vee f(r),\) as desired.
Proof of Theorem 6
-
From Construction to Postulates:
-
Part 1:
-
Case i, \(p \notin K\) or \(q \notin K:\) Then \(p \& q \notin K.\)Conjunctive overlap follows from C1 and the properties of full meet contraction.
-
Case ii, p, q ∈ K: Let \(\vdash f(p) \& f(q) \to f(p \& q).\) Then:
-
\(K \perp f(p \& q) \subseteq K \perp (f(p) \& f(q))\) (Lemma 4:1 and C1)
-
\(K\,{\sim}\,(f(p) \& f(q)) \subseteq K\,{\sim}\,f(p \& q)\) (Lemma 6)
-
\(K \cap \hbox{Cn} (\{\neg (f(p) \& f(q))\}) \subseteq K \cap \hbox{Cn} (\{\neg f(p \& q)\})\) (Lemma 5)
-
\((K \cap \hbox{Cn} (\{\neg (f(p)\})) \cap (K \cap \hbox{Cn} (\{\neg (f(q)\})) \subseteq K \cap \hbox{Cn} (\{\neg f(p \& q)\})\)
-
\((K\,{\sim}\,f(p)) \cap (K\,{\sim}\,f(q)) \subseteq K\,{\sim}\,f(p \& q)\) (Lemma 5)
-
\((K \div p) \cap (K \div q) \subseteq K \div (p \& q)\)
-
-
-
Part 2:
-
Case i: \(p \notin K\) : Then \(K \div p = K,\) and the postulate follows directly.
-
Case ii: \(q \notin K:\) Then \(p \& q \notin K,\) thus \(K \div (p \& q) = K\) and it follows from \(p \notin K \div (p \& q)\) that \(p \notin K\) so that we are back in case i.
-
Case iii, \(p, q \in K:\) Let \(p \notin K \div (p \& q).\) Then
-
\(p \notin K \cap \hbox{Cn} (\{\neg f(p \& q)\})\) (Lemma 5)
-
\(p \notin \hbox{Cn} (\{\neg f(p \& q)\})\) (since p ∈ K)
-
\(\nvdash\,\,\neg p \to f(p \& q)\)
-
\(\vdash f(p \& q) \to f(p)\) (C12)
-
\(K \perp f(p) \subseteq K \perp f(p \& q)\) (Lemma 4:1)
-
\(K\,{\sim}\,f(p \& q) \subseteq K\,{\sim}\,f(p)\) (Lemma 6)
-
\(K \div (p \& q) \subseteq K \div p\)
-
-
-
Part 3:
-
Case i: \(p \notin K\) or \(q \notin K:\) It follows from C1 that either \(f(p) \notin K\) or \(f(q) \notin K.\) Then either \(K \div p = K\) or \(K \div q = K,\) and the postulate follows directly.
-
Case ii: \(p, q \in K:\)
-
\(\vdash f(p \& q) \to f(p)\,\,\vee f(q)\) (C13)
-
\(\vdash (f(p)\,\,\vee f(q) \to\)
 K) → (f(p&q) →
K) → (f(p&q) → K)
K)(Since \(\vdash\)
 \(K \to f(p)\,\,\vee f(q),\) due to C1)
\(K \to f(p)\,\,\vee f(q),\) due to C1) -
\(\hbox{Cn} (\{f(p{\&}q) \to\)
 \(K\}) \subseteq \hbox{Cn} (\{f(p) \vee f(q) \to\)
\(K\}) \subseteq \hbox{Cn} (\{f(p) \vee f(q) \to\) K })
K }) -
\(\hbox{Cn} (\{f(p \& q) \to\)
 \(K\}) \subseteq \hbox{Cn} (\{f(p) \to\)
\(K\}) \subseteq \hbox{Cn} (\{f(p) \to\) K, f(q) →
K, f(q) → K })
K }) -
\(\hbox{Cn} (\{f(p \& q) \to\)
 \(K\}) \subseteq \hbox{Cn} (\hbox{Cn} (\{f(p) \to\)
\(K\}) \subseteq \hbox{Cn} (\hbox{Cn} (\{f(p) \to\) \(K\}) \cup \hbox{Cn} (\{f(q) \to\)
\(K\}) \cup \hbox{Cn} (\{f(q) \to\) K }))
K })) -
\(K \cap \hbox{Cn} (\{\neg f(p \& q)\}) \subseteq \hbox{Cn} ((K \cap \hbox{Cn} (\{\neg f(p)\})) \cup (K \cap \hbox{Cn} (\{\neg f(q)\})))\)
-
\(K\,{\sim}\,f(p \& q) \subseteq \hbox{Cn} ((K\,{\sim}\,f(p)) \cup (K\,{\sim}\,f(q)))\) (Lemma 5)
-
\(K \div (p \& q) \subseteq \hbox{Cn} ((K \div p) \cup (K \div q))\)
-
-
-
-
Part 4: Let p ∈ K and \(K \div p = K\,{\sim}\,q.\)
-
Case i, \(q \notin K\): It follows from C1 that \(f(q) \notin K,\) thus \(K \div q = K\,{\sim}\,q = K.\)
-
Case ii, q ∈ K:
-
\(K\,{\sim}\,f(p) = K\,{\sim}\,q\)
-
\(K \cap \hbox{Cn} (\{\neg f(p)\}) = K \cap \hbox{Cn} (\{\neg q\})\) (Lemma 5)
-
\(\vdash (f(p) \to\)
 K) \(\leftrightarrow\) (q →
K) \(\leftrightarrow\) (q → K)
K) -
\(\vdash f(p) \leftrightarrow q\) (Since \(\vdash\)
 K → f(p), due to C1, and \(\vdash\)
K → f(p), due to C1, and \(\vdash\) K → q.)
K → q.)
Using C14 we obtain \(K \div q = K\,{\sim}\,f(q) = K\,{\sim}\,f(f(p)) = K\,{\sim}\,f(p) = K \div p.\)
-
-
-
From Postulates to Construction:
-
Part 1:
-
\((K \div p) \cap (K \div q) \subseteq K \div (p \& q)\) (conjunctive overlap)
-
\(\vdash\)
 \((K \div (p \& q)) \to\)
\((K \div (p \& q)) \to\)
 \((K \div p)\,\,\vee\)
\((K \div p)\,\,\vee\)
 \((K \div q)\)
\((K \div q)\)
-
\(\vdash\) ((
 \((K \div p)\,\,\vee\)
\((K \div p)\,\,\vee\) \((K \div q)) \to\)
\((K \div q)) \to\) K) → (
K) → ( \((K \div (p \& q)) \to \)
\((K \div (p \& q)) \to \) K)
K)(since \(\vdash\)
 K → (
K → ( \((K \div p)\,\,\vee\)
\((K \div p)\,\,\vee\)
 \((K \div q)\))
\((K \div q)\)) -
\(\vdash\) (
 \((K \div p) \to\)
\((K \div p) \to\) K) & (
K) & ( \((K \div q) \to\)
\((K \div q) \to\) K) → (
K) → ( \((K \div (p \& q)) \to\)
\((K \div (p \& q)) \to\) K)
K) -
\(f(p) \& f(q) \to f(p \& q).\)
-
-
Part 2: Let p,q ∈ K and let \(\nvdash\,\,\neg p \to f(p \& q),\) i.e. \(\nvdash\,\,\neg p \to\) (
 \((K \div (p \& q)) \to\)
\((K \div (p \& q)) \to\)
 K). Since \(\vdash\)
K). Since \(\vdash\)
 K → p this is equivalent with \(\nvdash\)
K → p this is equivalent with \(\nvdash\)
 \((K \div (p \& q)) \to p.\) Hence \(p \notin K \div (p \& q),\) and conjunctive inclusion yields \(K \div (p \& q) \subseteq K \div p,\) thus \(\vdash\)
\((K \div (p \& q)) \to p.\) Hence \(p \notin K \div (p \& q),\) and conjunctive inclusion yields \(K \div (p \& q) \subseteq K \div p,\) thus \(\vdash\)
 \((K \div p) \to\)
\((K \div p) \to\)
 \((K \div (p \& q)).\) If follows from this and \(\vdash\)
\((K \div (p \& q)).\) If follows from this and \(\vdash\)
 K →
K → \((K \div (p \& q))\) that \(\vdash\) (
\((K \div (p \& q))\) that \(\vdash\) ( \((K \div (p \& q)) \to\)
\((K \div (p \& q)) \to\)
 K) → (
K) → ( \((K \div p) \to\)
\((K \div p) \to\)
 K). Hence, \(\vdash f(p \& q) \to f(p).\)
K). Hence, \(\vdash f(p \& q) \to f(p).\)
-
Part 3: \(K \div (p \& q) \subseteq \hbox{Cn} ((K \div p) \cup (K \div q))\) (weak conjunctive inclusion)
-
\(\vdash\)
 \((K \div p)\) &
\((K \div p)\) & \((K \div q) \to\)
\((K \div q) \to\) \((K \div (p \& q))\)
\((K \div (p \& q))\) -
\(\vdash\) (
 \((K \div (p \& q)) \to\)
\((K \div (p \& q)) \to\) K) → ((
K) → (( \((K \div p)\)) & (
\((K \div p)\)) & ( \((K \div q)) \to\)
\((K \div q)) \to\) K)
K)(since \(\vdash\)
 K →
K → \(K \div (p \& q)\))
\(K \div (p \& q)\)) -
\(\vdash\) (
 \((K \div (p \& q)) \to\)
\((K \div (p \& q)) \to\) K) → (
K) → ( \((K \div p) \to\)
\((K \div p) \to\) K) ∨ (
K) ∨ ( \((K \div q) \to\)
\((K \div q) \to\) K)
K) -
\(\vdash f(p \& q) \to f(p)\,\,\vee f(q)\)
-
-
Part 4: Let p ∈ K. From \(K \div p = K\,{\sim}\,f(p)\) and full meet identity follows \(K \div p = K \div f(p),\) i.e. \(K \div p = K \div\) (
 \((K \div p) \to\)
\((K \div p) \to\)
 K). It follows that \(\vdash\) (
K). It follows that \(\vdash\) ( \((K \div p) \to\)
\((K \div p) \to\)
 K) \(\leftrightarrow\) (
K) \(\leftrightarrow\) ( (\(K \div\) (
(\(K \div\) ( \((K \div p) \to\)
\((K \div p) \to\)
 K)) →
K)) →  K) i.e. \(\vdash f(p) \leftrightarrow f(f(p))\) as desired.
K) i.e. \(\vdash f(p) \leftrightarrow f(f(p))\) as desired.
-
Proof of Observation 8
-
Part 1: Let p, q ∈ K. If \(\vdash p\) then C2 yields \(\vdash f(p),\) from which C13 follows directly. If \(\nvdash\,\,p,\) then \(\nvdash\,\,p \& q,\) and C3 yields \(\nvdash\,\,\neg (p \& q) \to f(p \& q).\) It follows that either \(\nvdash\,\,\neg p \to f(p \& q)\) or \(\nvdash\,\,\neg q \to f(p \& q),\) and we can conclude from C12 that either \(\vdash f(p \& q) \to f(p)\) or \(\vdash f(p \& q) \to f(q).\) From this C13 follows directly.
-
Part 2: It follows from C4 that \(\vdash f(p) \& (f(p) \to p) \leftrightarrow p,\) hence C11 and C0 yield \(\vdash f(f(p)) \& f(f(p) \to p) \to f(p).\) From this and \(\vdash (f(p) \to p) \to f(f(p) \to p),\) that is obtained from C4, it follows truth-functionally that \(\vdash f(f(p)) \to f(p).\) Since the other direction follows directly from C4, this is sufficient to show that C14 holds.
Proof of Theorem 7
Directly from Theorems 3 and 6 and the standard axiomatic characterization of transitively relational partial meet contraction in terms of the eight postulates closure, inclusion, vacuity, success, extensionality, recovery, conjunctive overlap, and conjunctive inclusion (Alchourrón et al. 1985, p. 520).
Proof of Theorem 8
It follows from Theorem 6, parts 1 and 3, that (a) and (b) are equivalent. To see that (c) implies (a) whenever C3 and C4 hold (cf. Observation 3, part 3), note that it was shown by Alchourrón et al. (1985, p. 518–519) that relational partial meet contraction satisfies conjunctive overlap and by Rott (1993, pp. 1440–1441) that completedly relational partial meet contraction satisfies weak conjunctive inclusion.
It remains to be shown that (b) implies (c) whenever C3 and C4 hold. Let f satisfy the given properties. We define γ as follows:
We need to show (1) that \(\gamma (K \perp p) \subseteq K \perp p\) if \(K \perp p \neq \varnothing,\) (2) that \(\gamma (K \perp p) \neq \varnothing \) if \(K \perp p \neq \varnothing \) (thus 1 and 2 establish that γ is a selection function), (3) that γ completed, and (4) that γ is relational.
-
Part 1: If \(p \notin K,\) then it follows from C1 that \(f(p) \notin K,\) hence \(K \perp f(p) = K \perp p = \{K\}.\) If p ∈ K, then we use C4 to obtain \(\vdash p \to f(p).\) Lemma 4:1 yields \(K \perp f(p) \subseteq K \perp p.\)
-
Part 2: If \(K \perp p \neq \varnothing \) then \(p \notin \hbox{Cn} (\varnothing).\) There are two cases. First, if \(p \in K \setminus \hbox{Cn} (\varnothing),\) then C3 yields \(f(p) \notin \hbox{Cn} (\varnothing),\) thus \(K \perp f(p) \neq \varnothing.\) Secondly, if \(p \notin K,\) then C1 yields \(f(p) \notin K,\) thus \(K \perp f(p) \neq \varnothing.\)
-
Part 3: To show that γ is completed, let \(p \in K \setminus \hbox{Cn} (\varnothing)\) and let \(\cap \gamma (K \perp p) \subseteq X \in K \perp p.\) We need to show that \(X \in \gamma (K \perp p).\)
Since \(\gamma (K \perp p) = K \perp f(p)\) it follows from \(\cap \gamma (K \perp p) \subseteq X\) that \(\cap (K \perp f(p)) \subseteq X\) and then from Lemma 5 that f(p) →
 K ∈ X. Since \(X\,\,\nvdash\)
K ∈ X. Since \(X\,\,\nvdash\)
 \(K,\,\, X\,\,\nvdash\,\,f(p).\) Due to C1, Lemma 3 yields \(X \in K \perp f(p) = \gamma (K \perp p),\) as desired.
\(K,\,\, X\,\,\nvdash\,\,f(p).\) Due to C1, Lemma 3 yields \(X \in K \perp f(p) = \gamma (K \perp p),\) as desired. -
Part 4: (Cf. Rott 1993) We need to show that there is some relation \(\sqsubseteq \) such that the following identity holds for all p:
$$ \gamma (K \perp p) = \{X \in K \perp p \mid Y\,\sqsubseteq\,X \hbox{ for all } Y \in K \perp p\} $$
We will show this for \(\sqsubseteq \) defined as follows:
-
\(Y\,\sqsubseteq\,X\) iff there is some s such that \( Y \in K \perp s\) and \(X \in \gamma (K \perp s)\)
For one direction of the identity, let \(X \in \gamma (K \perp p).\) Then it holds for all \(Y \in K \perp p\) that \(Y\,\sqsubseteq\,X,\) thus:
For the other direction let \(X \in K \perp p\) and \(Y\,\sqsubseteq\,X\) for all \(Y \in K \perp p.\) Then for each \(Y\in K \perp p\) there is a sentence s(Y) ∈ K such that \(Y \in K \perp s(Y)\) and \(X \in \gamma (K \perp s(Y)),\) i.e. \(X \in K \perp f(s(Y)).\) Let \(S = \{s(Y) \mid Y \in K \perp p\}.\) Then using Definition 6, \(K \perp p \subseteq K \bigtriangleup S = \cup \{K \perp s(Y) \mid s(Y) \in S\}.\)
We first need to show that \(S \vdash p.\) Suppose to the contrary that \(S\,\,\nvdash\,\,p.\) Since \(S \subseteq K\) it then follows from Lemma 1 (that uses Zorn’s lemma) that there is some Z such that \(S \subseteq Z \in K \perp p.\) For all s(Y) ∈ S we have \(Z \notin K \perp s(Y),\) hence \(Z \notin K \bigtriangleup S\) so that \(K \perp p \not \subseteq K \bigtriangleup S.\) We can conclude from this contradiction that \(S \vdash p.\)
Due to compactness there is a finite subset S′ of S such that \(S^{\prime} \vdash p.\) Let \(W \in K \perp p.\) Then since \(S^{\prime} \vdash p,\,\, S^{\prime} \not \subseteq W.\) It follows that there is some \(s(Y) \in S^{\prime}\) such that \(s(Y) \notin W.\) It follows from Lemma 3 that \(W \in K \perp s(Y).\) Since this holds for all \(W \in K \perp p,\) we can conclude that \(K \perp p \subseteq K \bigtriangleup S^{\prime}.\) By repeated application of Lemma 4:2 we obtain \(K \perp p \subseteq K \perp\)
 S′.
S′.
Since \(X \in K \perp f(s(Y))\) for all \(s(Y) \in S^{\prime},\) we can use Lemma 4:3 to obtain \(X \in K \perp \bigvee \{f(s(Y)) \mid s(Y) \in S^{\prime}\}\) (where \(\bigvee\) denotes the disjunction of all elements of a set). It follows from C13 and Lemma 4:1 that \(X \in K \perp f\)( S′).
S′).
It follows from \(S^{\prime} \vdash p\) and C11 that:
-
\(\vdash f(p) \& f\)(p →
 S′) → f (
S′) → f ( S′), hence
S′), hence -
\(K \perp f\)(
 S′) \(\subseteq K \perp\) (f(p)
S′) \(\subseteq K \perp\) (f(p) f (p →
f (p → S′)) (Lemma 4:1)
S′)) (Lemma 4:1) -
\(K \perp f\)(
 S′) \(\subseteq K \perp f(p) \cup K \perp f\)(p →
S′) \(\subseteq K \perp f(p) \cup K \perp f\)(p → S′) (Lemma 4:2)
S′) (Lemma 4:2) -
\((K \perp p) \cap\) (K ⊥ f (
 S′)) \(\subseteq (K \perp p) \cap ((K \perp f(p)) \cup\) (K ⊥ f (p →
S′)) \(\subseteq (K \perp p) \cap ((K \perp f(p)) \cup\) (K ⊥ f (p → S′)))
S′)))
It follows from C4 that (p →  S′) → f(p →
S′) → f(p →  S′) and then from Lemma 4:1 that \(K \perp\)(f(p →
S′) and then from Lemma 4:1 that \(K \perp\)(f(p → S′)) \(\subseteq \, K \perp\) (p →
S′)) \(\subseteq \, K \perp\) (p → S′). It follows from Lemma 4:3 that \((K \perp p) \,\cap\) (K ⊥ (p →
S′). It follows from Lemma 4:3 that \((K \perp p) \,\cap\) (K ⊥ (p → S′)) = \(\varnothing.\) Hence, \((K \perp p) \,\cap\) (K ⊥ f(p →
S′)) = \(\varnothing.\) Hence, \((K \perp p) \,\cap\) (K ⊥ f(p → S′)) = \(\varnothing.\) We can therefore simplify the above to:
S′)) = \(\varnothing.\) We can therefore simplify the above to:
We know from C4 and Lemma 4:1 that \(K \perp f(p) \subseteq K \perp p\) and thus obtain:
Since by assumption X ∈ K ⊥ p and since we have shown that \(X \in K \perp f\) ( S′) it follows that \(X \in K \perp f(p) = \gamma (K \perp p),\) as desired.
S′) it follows that \(X \in K \perp f(p) = \gamma (K \perp p),\) as desired.
Rights and permissions
About this article
Cite this article
Hansson, S.O. Specified Meet Contraction. Erkenn 69, 31–54 (2008). https://doi.org/10.1007/s10670-007-9088-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-007-9088-4





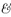
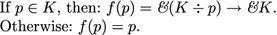 In order to verify the construction we need to show that the identity
In order to verify the construction we need to show that the identity