Skip to main content
SpringerLink
Log in

Unifying statistically autonomous and mathematical explanations

  • Published:
Biology & Philosophy Aims and scope Submit manuscript

Abstract

A subarea of the debate over the nature of evolutionary theory addresses what the nature of the explanations yielded by evolutionary theory are. The statisticalist line is that the general principles of evolutionary theory are not only amenable to a mathematical interpretation but that they need not invoke causes to furnish explanations. Causalists object that construction of these general principles involves crucial causal assumptions. A recent view claims that some biological explanations are statistically autonomous explanations (SAEs) whereby phenomena are accounted for statistically and which prescind from micro-causal details. I raise three major problems for this account and then advance a view which unifies SAEs as mathematical explanations: the MSAE view. The MSAE view not only resolves the issues bedeviling the original SAE account but serves to importantly broaden the class of non-causal explanations in population biology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

(Adapted from Stigler 2010)

Fig. 2

Adapted from Galton 1889)

Fig. 3

Similar content being viewed by others

Notes

  1. What Hacking has in mind here is what might also be termed “epistemic irreducibility”: the macro-level theory or explanation cannot be derived from nor reduced to the micro-level theory in principle (Fletcher et al. 2019).

  2. Alternative accounts of statistical explanation include Marc Lange’s really statistical (RS) view (Lange 2013, 2017) and Batterman and Rice’s minimal models account (Batterman and Rice 2014). For Lange, regression cases are not statistically autonomous since the explanandum in these cases can be accounted for causally (Lange 2013). The fact that these explananda admit of pluralism undercuts their status as SAEs.

  3. The emphasis on approximation is apropos of the fact that a normal distribution involves infinite trials. Therefore, real-world populations can only at best approximate a normal distribution.

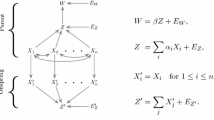
  4. Ariew et al.’s (2017) treatment of Galton’s methodology is contested by Witteveen (2019). Witteveen’s objections are mostly historical and concern the Galton case particularly. Since my ambit is to unpack the SAE as a general explanatory framework, these objections will not be addressed here.

  5. A further step in demonstrating that biological populations which involve heredity could be represented as stochastic ensembles are Galton’s experiments with sweet peas. These details are left out here since focus is trained mostly at the primary explanatory moves in the case. For these details, see Ariew et al. (2017), pp. 67–68.

  6. One may object that this list (D1-D3) is not exhaustive since it excludes possibilities such as D4: “The gas is not an SAE and it could be either causal/non-causal” or D5: “The gas is an SAE and it could be either causal/non-causal.” The point of O2 is to show that whichever way the causal/non-causal status of SAEs is filled out in a determinate fashion, the SAE account as presently constructed is problematic. Falling back on agnosticism fails to settle the issue since each of the determinate causal/non-causal possibilities imply difficulties for the SAE account.

  7. This inquiry parallels the debate in the philosophy of physics over the nature of continuum and infinite idealizations whereby the macro-level theory fails to reduce to the micro-level theory. This gives rise to a similar question about the status of these idealizations: are they explanatorily indispensable in principle or rather explanatorily dipsensable (Shech 2013; Fletcher et al. 2019).

  8. As may be apparent from these two criteria, the REDC condition is clearly influenced by Lewis’ “Best Systems Analysis” of lawhood (Lewis 1994).

  9. Further examples of topological mathematical explanations are Pincock’s “Bridges of Königsberg case (2007) and Lange’s double pendulum case (Lange 2013). Huneman (2010) includes a further catalogue of such cases.

  10. For a clearer exposition, I have avoided constructing these arguments as valid ones here.

References

  • Andersen H (2016) Complements, not competitors: causal and mathematical explanations. Br J Philos Sci 69(2):485–508

    Article  Google Scholar 

  • Ariew A, Rice C, Rowher Y (2015) Autonomous statistical explanations and natural selection. Br J Philos Sci 66:635–658

    Article  Google Scholar 

  • Ariew A, Rowher Y, Rice C (2017) Galton, reversion and the quincunx: the rise of statistical explanation. Stud Hist Philos Sci Part C Stud Hist Philos Biol Biomed Sci 66:63–72

    Article  Google Scholar 

  • Baker A (2005) Are there genuine mathematical explanations of physical phenomena? Mind 454(114):223–238

    Article  Google Scholar 

  • Baker A, Colvyan M (2011) Indexing and mathematical explanation. Philosophia Mathematica 19:323–334

    Article  Google Scholar 

  • Baron S (2016) Explaining mathematical explanation. Philos Quart 66:458–480

    Article  Google Scholar 

  • Baron S (2019) Mathematical explanation by law. Br J Philos Sci 70:683–717

    Article  Google Scholar 

  • Batterman RW (2018) Autonomy of theories: an explanatory problem. Noûs 52(4):858–873

    Article  Google Scholar 

  • Batterman RW, Rice C (2014) Minimal model explanations. Philos Sci 81:349–376

    Article  Google Scholar 

  • Cartwright N (1979) Causal laws and effective strategies. Noûs 13(4):419–437

    Article  Google Scholar 

  • Craver CF, Kaplan D (2020) Are more details better? On the norms of completeness for mechanistic explanations. Br J Phi Sci 71:287–319

    Article  Google Scholar 

  • Crow JF, Kimura M (2009) An introduction to population genetics theory. Blackburn Press, Caldwell

    Google Scholar 

  • Fletcher SC et al (2019) Infinite idealizations in science: an introduction. Synthese 196:1657–1669

    Article  Google Scholar 

  • Galton F (1877) Typical laws of heredity. Proc R Inst 8:282–301

    Google Scholar 

  • Galton F (1889) Natural inheritance. Macmillan and Co., London

    Book  Google Scholar 

  • Hacking I (1990) The taming of chance. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Hacking I (1992) Statistical language, statistical truth and statistical reason: the self-authentication of a style of scientific reason. In: McMullin E (ed) The social dimension of science. University of Notre Dame Press, Notre Dame, pp 130–157

    Google Scholar 

  • Hempel C (1965) Aspects of scientific explanation and other essays in the philosophy of science. Free Press, New York

    Google Scholar 

  • Hempel C, Oppenheim P (1948) Studies in the logic of explanation. Philos Sci 15:135–175

    Article  Google Scholar 

  • Huneman P (2010) Topological explanations and robustness in biological sciences. Synthese 177:213–245

    Article  Google Scholar 

  • Ishida Y, Rosales A (2020) The origins of the stochastic theory of population genetics: the Wright–Fisher model. Stud Hist Philos Sci Part C Stud Hist Philos Biol Biomed Sci 79:1–8

    Google Scholar 

  • Jackson F, Petit P (1991) Program explanation: a general perspective. Analysis 50(2):107–117

    Article  Google Scholar 

  • Kaplan DM, Craver CF (2011) The explanatory force of dynamical and mathematical models in neuroscience: a mechanistic perspective. Philos Sci 78:601–627

    Article  Google Scholar 

  • Lange M (2013) Really statistical explanations and genetic drift. Philos Sci 80(2):169–188

    Article  Google Scholar 

  • Lange M (2017) Because without cause. Oxford University Press, Oxford

    Google Scholar 

  • Levins R (1966) The strategy of model building in population biology. Ameri Sci 54:421–431

    Google Scholar 

  • Lewis D (1994) Humean supervenience debugged. Mind 103:473–490

    Article  Google Scholar 

  • Lyon A (2012) Mathematical explanations of empirical facts, and mathematical realism. Aust J Philos 90(3):559–578

    Article  Google Scholar 

  • Matthen M, Ariew A (2002) Two ways of thinking about fitness and natural selection. J Phil 99(2):55–83

    Article  Google Scholar 

  • Matthen M, Ariew A (2009) Selection and causation. Philos Sci 76:201–224

    Article  Google Scholar 

  • Millstein R (2006) Natural selection as a population-level causal process. Br J Philos Sci 57(4):627–653

    Article  Google Scholar 

  • Millstein R, Skipper RAJ, Dietrich MR (2009) (Mis)interpreting mathematical models: drift as a physical process. Philos Theory Biol 1:e002

    Google Scholar 

  • Morrison M (2004) Population genetics and population thinking: mathematics and the role of the individual. Philos Sci 71:1189–1200

    Article  Google Scholar 

  • Otsuka J (2015) Using causal models to integrate proximate and ultimate causation. Biol Philos 30(1):19–37

    Article  Google Scholar 

  • Otsuka J (2016) A critical review of the statisticalist debate. Biol Philos 31:459–482

    Article  Google Scholar 

  • Pincock C (2007) A role for mathematics in the physical sciences. Noûs 41(2):253–275

    Article  Google Scholar 

  • Pincock C (2015) Abstract explanations in science. Br J Philos Sci 66:857–882

    Article  Google Scholar 

  • Putnam H (1975) Philosophy and our mental life. Mind, Language and reality: philosophical papers, vol 2. Cambridge University Press, Cambridge, pp 291–303

    Chapter  Google Scholar 

  • Reisman K, Forber P (2005) Manipulation and the causes of evolution. Philos Sci 72:1113–1123

    Article  Google Scholar 

  • Reutlinger A (2018) Extending the counterfactual theory of explanation. In: Reutlinger A, Saatsi J (eds) Explanation beyond causation. Oxford University Press, Oxford, pp 74–95

    Chapter  Google Scholar 

  • Rice C, Rowher Y, Ariew A (2019) Explanatory schema and the process of model building. Synthese 196:4735–4757

    Article  Google Scholar 

  • Salmon W (1971) Statistical explanation. In: Salmon W (ed) Statistical explanation and statistical relevance. University of Pittsburgh Press, Pittsburgh, pp 29–87

    Chapter  Google Scholar 

  • Salmon W (1989) Four decades of scientific explanation. University of Pittsburgh Press, Pittsburgh

    Google Scholar 

  • Shech E (2013) What is the ‘paradox of phase transitions?’ Philos Sci 80:1170–1181

    Article  Google Scholar 

  • Sober E (1984) The nature of selection: evolutionary theory in philosophical focus. University of Chicago Press, Chicago

    Google Scholar 

  • Steiner M (1978) Mathematics, explanation and scientific knowledge. Noûs 12:17–28

    Article  Google Scholar 

  • Stephens C (2004) Selection, drift, and the “forces” of evolution. Philos Sci 71(4):550–570

    Article  Google Scholar 

  • Stigler SM (2010) Darwin, Galton and the statistical enlightenment. JR Stat Soc Ser A Stat Soc 173(3):469–482

    Article  Google Scholar 

  • Strevens M (2008) Depth. Harvard University Press, Cambridge

    Google Scholar 

  • Strevens M (2018) The mathematical route to causal understanding. In: Reutlinger A, Saatsi J (eds) Explanation beyond causation. Oxford University Press, Oxford, pp 96–116

    Google Scholar 

  • Walsh DM (2007) The pomp of superfluous causes: the interpretation of evolutionary theory. Philos Sci 74:281–303

    Article  Google Scholar 

  • Walsh DM, Ariew A, Matthen M (2017) Four pillars of statisticalism. Philos Theory Biol 9(1):1–18

    Google Scholar 

  • Weisberg M (2007) Who is a modeler? Br J Philos Sci 58(2):207–233

    Article  Google Scholar 

  • Weisberg M (2013) Simulation and similarity. Oxford University Press, Oxford

    Book  Google Scholar 

  • Witteveen J (2019) Regression explanation and statistical autonomy. Biol Philos: 34–51

  • Woodward JB (2003) Making things happen: a theory of causal explanation. Oxford University Press, New York

    Google Scholar 

Download references

Acknowledgements

The author would like to thank Andre Ariew for helpful conversations pertaining to the draft.

Funding

No funding was received to assist in the preparation of this manuscript.

Author information

Authors and Affiliations

  1. University of Missouri-Columbia, 438 Strickland Hall, Columbia, MO, 65201, USA

    Travis L. Holmes

Authors
  1. Travis L. Holmes
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Travis L. Holmes.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Holmes, T.L. Unifying statistically autonomous and mathematical explanations. Biol Philos 36, 33 (2021). https://doi.org/10.1007/s10539-021-09808-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10539-021-09808-z

Keywords

Search

Navigation