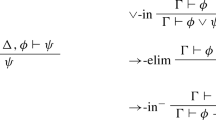Abstract
Cook regards Sorenson’s so-called ‘the no-no paradox’ as only a kind of ‘meta-paradox’ or ‘quasi-paradox’ because the symmetry principle that Sorenson imposes on the paradox is meta-theoretic. He rebuilds this paradox at the object-language level by replacing the symmetry principle with some ‘background principles governing the truth predicate’. He thus argues that the no-no paradox is a ‘new type of paradox’ in that its paradoxicality depends on these principles. This paper shows that any theory (not necessarily meeting Cook’s background principles) is inconsistent with the T-schema instances for the no-no sentences, plus the T-schema instance for a Curry sentence associated with the symmetry of the no-no sentences. It turns out that the no-no paradox still depends on the problematic instances of the T-schema in a way that the liar paradox does. What distinguishes the no-no paradox is the T-schema instance for the above Curry sentence, which encodes Sorensen’s symmetry principle at the object-language level.
Similar content being viewed by others
Notes
Cook’s main lemma for the paradoxicality of the no-no pair is that if the truth predicate ‘T(...)’ obeys \(\mathbf{N} \), \(\mathbf{K} \), and \(\mathbf{4} \), then the two no-no sentences are provably equivalent. In his proof, Cook cites Löb’s theorem as follows: “If ‘T(...)’ is a provability predicate, then ‘T(...)’ satisfies Löb’s theorem.” Cook points out in a footnote that his proof ‘emphasizes the connections between the no-no pair and the Curry Paradox.’ Also, he takes Löb’s theorem as “a ‘consistent’ version of the Curry construction.” See Cook (2011, 472).
Halbach et al. ’s result [Example 42 in their paper] assumes the Barcan schema and the \(\omega \)-rule instead of schema \(\mathbf{4} \). To prove the inconsistency of the theory in question, they appeal to a much more sophisticated paradox (McGee’s paradox). See the reference as mentioned above for details.
We benefited from one referee’s suggestions, adding this new section. We would like to express our sincere thanks to him/her.
See (Hsiung 2017, p. 888) for more details about the Boolean system.
We refer the reader to Hungerford (1974) for more information from group theory.
For a Boolean formula \(f(p_1, \ldots , p_{n})\), we still use f to denote the correponding Boolean function. In this way, the condition associated with Eq. (2) can be expressed as the functional Eq. \(f_{\pi (i)}\left( p_{1}, \ldots , p_{n}\right) =f_i\left( p_{\pi (1)}, \ldots , p_{\pi (n)}\right) \).
This paradox is also called Jourdain’s paradox, named after a British logician in the late nineteenth and early twentieth centuries. However, it is believed that John Buridan, a Medieval logician, first proposed this paradox. See for instance Sorensen (2001, 180).
In other words, this list takes the symmetric group on I as its symmetry group. As a contrast, for any \(n >1\), the symmetry group for the n-element enlarged no-no paradox is a proper subgroup of the symmetric group on I. For instance, for \(n=4\), it can be verified that the symmetry group of the 4-element enlarged no-no paradox contains only four permutations, say (1234), (1432), (13)(24), and the identity mapping. In this sense, we can say that the set of above sentences bears more symmetry than the 4-element enlarged no-no paradox.
Generally, for any \(n>1\), and for any non-trivial sub-group \(\mathcal {G}\) of the symmetric group on \(\{1, \ldots , n\}\), we can construct a no-no-like paradox such that its symmetry group is just \(\mathcal {G}\). The investigation of this issue is left for further studies.
Here, a tacit agreement is that by ‘classical logic’, we mean any theory without the restriction of any principle regarding truth. And, the theory, of course, must be ‘sufficiently strong’ so that we can construct a variety of self-referential sentences by diagonalization.
It should be noted that corresponding to Theorem 3(ii) or Theorem 6(ii), another possible definition is to appeal to the condition ‘the set \(\Gamma \cup \{T\ulcorner {\kappa }\urcorner \leftrightarrow \kappa \}\cup \{T\ulcorner {S_i}\urcorner \leftrightarrow S_i{\ \mid \ }1\le i\le n\}\) is inconsistent, where \(\kappa \) is a Curry sentence for some of the sentences \(S_1\leftrightarrow S_{\pi (1)}\), ..., and \(S_n\leftrightarrow S_{\pi (n)}\).’ The following discussions also apply mutatis mutandis to this definition.
This technique is from (McGee 1992, 238). We are grateful to an anonymous referee for pointing out the replacement of \(\kappa \) by \(\phi \) might weaken the role of \(\kappa \) in the previous definition.
Cook also discusses the truthmaker gap, a topic that we do not touch in this paper.
See (Sorensen 2001, 170). When Sorensen proposes this paradox, he also discusses Yablo’s paradox (Sorensen calls it ‘the descending liar’). Among all well-known paradoxes, Yablo’s paradox is one of the most controversial paradoxes. There are lots of discussions around whether Yablo’s paradox belongs to the liar type. Many discussions, as Leitgeb (2002) pointed out, are (unfortunately) due to different definitions of what we call the liar type or liar-like paradoxes. Only a clear-cut definition can settle the disputes. As far as the definition given in the previous section is concerned, Yablo’s paradox is not liar-type. See Ketland (2005) for proof. See also Cook (2014) for an encyclopedic investigation on Yablo’s paradox.
References
Armour-Garb, B., & Woodbridge, J. A. (2006). Dialetheism, semantic pathology, and the open pair. Australasian Journal of Philosophy, 84(3), 395–416.
Boolos, G. (1993). Logic of Provability. Cambridge University Press.
Cook, R. T. (2011). The no-no paradox is a paradox. Australasian Journal of Philosophy, 89(3), 467–482.
Cook, R. T. (2014). The Yablo Paradox: An Essay on Circularity. Oxford University Press.
Goldstein, L. (1992). ‘This statement is not true’ is not true. Analysis, 52(1), 1–5.
Halbach, V., Leitgeb, H., & Welch, P. (2003). Possible-worlds semantics for modal notions conceived as predicates. Journal of Philosophical Logic, 32(2), 179–223.
Herzberger, H. G. (1982). Notes on naive semantics. Journal of Philosophical Logic, 11(1), 61–102.
Hsiung, M. (2017). Boolean paradoxes and revision periods. Studia Logica, 105(5), 881–914.
Hungerford, T. W. (1974). Algebra. Graduate Texts in Mathematics. Springer.
Ketland, J. (2005). Yablo’s paradox and \(\omega \)-inconsistency. Synthese, 145(3), 295–302.
Leitgeb, H. (2002). What is a self-referential sentence? Critical remarks on the alleged (non-)circularity of Yablo’s paradox. Logique et Analyse, 45(177–178), 3–14.
Löb, M. H. (1955). Solution of a problem of Leon Henkin. The Journal of Symbolic Logic, 20(2), 115–118.
McGee, V. (1992). Maximal consistent sets of instances of Tarski’s schema (T). Journal of Philosophical Logic, 21(3), 235–241.
Sorensen, R. (2001). Vagueness and Contradiction. Oxford University Press.
Wen, L. (2001). Semantic paradoxes as equations. Mathematical Intelligencer, 23(1), 43–48.
Yablo, S. (1985). Truth and reflection. Journal of Philosophical Logic, 14(3), 297–349.
Acknowledgements
Thanks to two anonymous referees for their thoughtful and constructive comments, which have led to significant improvements.
Funding
This research has been supported by National Social Science Foundation of China (grant number 19BZX136).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Hsiung, M. In what sense is the no-no paradox a paradox?. Philos Stud 179, 1915–1937 (2022). https://doi.org/10.1007/s11098-021-01738-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-021-01738-6