Abstract
We show that \( VTC ^0\), the basic theory of bounded arithmetic corresponding to the complexity class \(\mathrm {TC}^0\), proves the \( IMUL \) axiom expressing the totality of iterated multiplication satisfying its recursive definition, by formalizing a suitable version of the \(\mathrm {TC}^0\) iterated multiplication algorithm by Hesse, Allender, and Barrington. As a consequence, \( VTC ^0\) can also prove the integer division axiom, and (by our previous results) the \( RSUV \)-translation of induction and minimization for sharply bounded formulas. Similar consequences hold for the related theories \(\Delta ^b_1\text{- } CR \) and \(C^0_2\). As a side result, we also prove that there is a well-behaved \(\Delta _0\) definition of modular powering in \(I\Delta _0+ WPHP (\Delta _0)\).
Similar content being viewed by others
Availability of data and material
Not applicable.
Notes
Originally, \(\mathrm {TC}^0\) was introduced as a nonuniform circuit class by Hajnal et al. [12], but in this paper we always mean the \(\mathrm {DLOGTIME}\)-uniform version of the class, which gives a robust notion of “fully uniform” \(\mathrm {TC}^0\) with several equivalent definitions across various computation models (cf. [4]). Likewise for \(\mathrm {AC}^0\).
Conventionally, our \(Y\mathrm {rem}~X\) is written as just \(Y\bmod X\). Since we will frequently mix this notation with the \(Y\equiv Y'\pmod X\) congruence notation, we want to distinguish the two more clearly than by relying on the typographical difference between \(Z=Y\bmod X\) and \(Z\equiv Y\pmod X\), considering also that many authors write the latter as \(Z\equiv Y\mod X\), or even \(Z=Y\mod X\).
We could make \({{\,\mathrm{lh}\,}}(X)\) and \(X_i\) \(\Sigma ^B_0\)-definable using a more elaborate definition of R: e.g., indicate the start of \(X_i\) in R not just by a single 1-bit, but by \(1+v_2(i)\) 1-bits (followed by at least one 0-bit). We leave it to the reader’s amusement to verify that this encoding is \(\Sigma ^B_0\)-decodable, and that it can encode \(\langle X_i:i<n\rangle \) using \(O\bigl (n+\sum _i|X_i|\bigr )\) bits. But crucially, proving the latter still requires \( VTC ^0\), or at least some form of approximate counting that allows close enough estimation of \(\sum _{j<i}|X_j|\). Thus, we do not really accomplish much with this more complicated scheme.
More precisely: for fixed \(\vec {a}=\langle a_i:i<l\rangle \), we prove by induction on \(l'\le l\) that (18) holds for \(\langle a_i:i<l'\rangle \), which is a \(\Sigma ^B_0(\mathrm {imul})\) property. Most proofs by induction in this section should be interpreted similarly.
A subtle point here is that we rely on
 : otherwise, if \(c_t=0\) and \(\vec {z}_t=\vec {2}\), then Definition 5.20 makes \(b_t=-1\) rather than \(b_t=2\), in which case \(b_t\xi _n(\vec {1})\) is off by 1 from \(\xi _n(b_t\vec {1})-c_t\) in the argument above. That is, the given proof only works unless \(k=1\) and \(m_0=3\). However, in the latter case, all the numbers involved are standard, and one can check that in actual reality, always \(b_t\in \{0,1\}\), hence the bad case does not arise.
: otherwise, if \(c_t=0\) and \(\vec {z}_t=\vec {2}\), then Definition 5.20 makes \(b_t=-1\) rather than \(b_t=2\), in which case \(b_t\xi _n(\vec {1})\) is off by 1 from \(\xi _n(b_t\vec {1})-c_t\) in the argument above. That is, the given proof only works unless \(k=1\) and \(m_0=3\). However, in the latter case, all the numbers involved are standard, and one can check that in actual reality, always \(b_t\in \{0,1\}\), hence the bad case does not arise.
References
Apostol, T.M.: Introduction to Analytic Number Theory. Undergraduate Texts in Mathematics, Springer, New York (1976)
Atserias, A.: Improved bounds on the Weak Pigeonhole Principle and infinitely many primes from weaker axioms. In: Sgall, J., Pultr, A., Kolman, P. (eds.) Mathematical Foundations of Computer Science 2001. Lecture Notes in Computer Science, vol. 2136, pp. 148–158. Springer, New York (2001)
Atserias, A.: Improved bounds on the Weak Pigeonhole Principle and infinitely many primes from weaker axioms. Theor. Comput. Sci. 295, 27–39 (2003)
Barrington, D.A.M., Immerman, N., Straubing, H.: On uniformity within \(\mathit{NC}^1\). J. Comput. Syst. Sci. 41(3), 274–306 (1990)
Beame, P.W., Cook, S.A., Hoover, H.J.: Log depth circuits for division and related problems. SIAM J. Comput. 15(4), 994–1003 (1986)
Berarducci, A., D’Aquino, P.: \(\Delta _0\)-complexity of the relation \(y=\prod _{i\le n}F(i)\). Ann. Pure Appl. Logic 75(1–2), 49–56 (1995)
Buss, S.R.: Bounded Arithmetic. Bibliopolis, Naples (1986). Revision of 1985 Princeton University Ph.D. thesis
Chiu, A.Y., Davida, G.I., Litow, B.E.: Division in logspace-uniform \(\mathit{NC}^1\). RAIRO Theor. Inform. Appl. 35(3), 259–275 (2001)
Cook, S.A., Nguyen, P.: Logical Foundations of Proof Complexity. Perspectives in Logic. Cambridge University Press, New York (2010)
D’Aquino, P.: Local behaviour of the Chebyshev theorem in models of \(I\Delta _0\). J. Symb. Log. 57(1), 12–27 (1992)
Hájek, P., Pudlák, P.: Metamathematics of First-Order Arithmetic. Perspectives in Mathematical Logic, 2nd edn. Springer, New York (1993)
Hajnal, A., Maass, W., Pudlák, P., Szegedy, M., Turán, G.: Threshold circuits of bounded depth. J. Comput. Syst. Sci. 46(2), 129–154 (1993)
Hesse, W., Allender, E., Barrington, D.A.M.: Uniform constant-depth threshold circuits for division and iterated multiplication. J. Comput. Syst. Sci. 65(4), 695–716 (2002)
Jeřábek, E.: Abelian groups and quadratic residues in weak arithmetic. Math. Log. Q. 56(3), 262–278 (2010)
Jeřábek, E.: Open induction in a bounded arithmetic for \({\rm TC}^0\). Arch. Math. Logic 54(3–4), 359–394 (2015)
Johannsen, J.: Weak bounded arithmetic, the Diffie-Hellman problem, and Constable’s class \(K\). In: Proceedings of the 14th Annual IEEE Symposium on Logic in Computer Science, pp. 268–274 (1999)
Johannsen, J., Pollett, C.: On proofs about threshold circuits and counting hierarchies (extended abstract). In: Proceedings of the 13th Annual IEEE Symposium on Logic in Computer Science, pp. 444–452 (1998)
Johannsen, J., Pollett, C.: On the \(\Delta ^b_1\)-bit-comprehension rule. In: Buss, S.R., Hájek, P., Pudlák, P. (eds.) Logic Colloquium ’98: Proceedings of the 1998 ASL European Summer Meeting Held in Prague, Czech Republic, pp. 262–280. ASL (2000)
Müller, S.: Polylogarithmic cuts in models of \({ V}^0\). Logic. Methods Comput. Sci. 9(1), 16 (2013)
Nelson, E.: Predicative Arithmetic. Mathematical Notes, vol. 32. Princeton University Press, Princeton (1986)
Nepomnjaščij, V.A.: Rudimentary predicates and Turing calculations. Doklady Akademii Nauk SSSR 195(2), 282–284 (1970). [English translation in: Soviet Mathematics – Doklady 11 (1970), no. 6, pp. 1462–1465]
Nguyen, P.: Bounded reverse mathematics. PhD thesis, University of Toronto (2008)
Nguyen, P., Cook, S.A.: Theories for \(TC^0\) and other small complexity classes. Logic. Methods Comput. Sci. 2(1), 39 (2006)
Parberry, I., Schnitger, G.: Parallel computation with threshold functions. J. Comput. Syst. Sci. 36(3), 278–302 (1988)
Paris, J.B., Wilkie, A.J.: Counting \(\Delta _0\) sets. Fundam. Math. 127(1), 67–76 (1987)
Paris, J.B., Wilkie, A.J., Woods, A.R.: Provability of the pigeonhole principle and the existence of infinitely many primes. J. Symb. Log. 53(4), 1235–1244 (1988)
Woods, A.R.: Some problems in logic and number theory, and their connections. PhD thesis, University of Manchester (1981)
Zambella, D.: Notes on polynomially bounded arithmetic. J. Symb. Log. 61(3), 942–966 (1996)
Zambella, D.: End extensions of models of linearly bounded arithmetic. Ann. Pure Appl. Logic 88(2–3), 263–277 (1997)
Funding
The research was supported by grant 19-05497S of GA ČR. The Institute of Mathematics of the Czech Academy of Sciences is supported by RVO: 67985840.
Author information
Authors and Affiliations
Contributions
There is only one author.
Corresponding author
Ethics declarations
Conflict of interest
The author has no conflicts of interest to declare.
Code availability
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jeřábek, E. Iterated multiplication in \( VTC ^0\). Arch. Math. Logic 61, 705–767 (2022). https://doi.org/10.1007/s00153-021-00810-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-021-00810-6


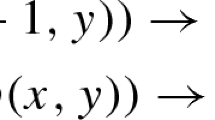

 : otherwise, if
: otherwise, if  such that there are exactly i smaller primes with this property.
such that there are exactly i smaller primes with this property.