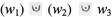Abstract
While the analytical philosophy of science regards inconsistent theories as disastrous, Chomsky allows for the temporary tolerance of inconsistency between the hypotheses and the data. However, in linguistics there seem to be several types of inconsistency. The present paper aims at the development of a novel metatheoretical framework which provides tools for the representation and evaluation of inconsistencies in linguistic theories. The metatheoretical model relies on a system of paraconsistent logic and distinguishes between strong and weak inconsistency. Strong inconsistency is destructive in that it leads to logical chaos. In contrast, weak inconsistency may be constructive, because it is capable of accounting for the simultaneous presence of seemingly incompatible structures. However, paraconsistent logic cannot grasp the dynamism of the emergence and resolution of weak inconsistencies. Therefore, the metatheoretical approach is extended to plausible argumentation. The workability of this metatheoretical model is tested with the help of a detailed case study on an analysis of discontinuous constituents in Government-Binding Theory.










Similar content being viewed by others
Notes
That is, without the degree word, sentential clauses cannot appear in the sentence. Moreover, the finiteness of the complement clause depends on the choice of the degree word \((so + that {\ldots }; too + to {\ldots }; enough + that/to {\ldots })\).
For evidence for this claim, cf. the examples (1)–(2) and (3)–(10), respectively, in Baltin (1987: 11f.).
In the case of enough, the adjective precedes the degree word.
This formulation is vague because it does not specify in what kind of position the sentential complement appears at the end of the clause. For example, it leaves open the question of whether we have to deal with a position adjoined to S’ from outside of S or with a position within S, that is, within the internal structure of the clause.
Cf.: “[...] it seems that degree words combine with sentential complements to form linguistic units in English (and in other languages) in exactly the same fashion as do verbs, adjectives, nouns, and prepositions.” (Baltin 1987: 12)
Node \(A\) c-commands node \(B\) if the first branching node dominating \(A\) also dominates \(B\) and neither \(A\) nor \(B\) dominate each other.
That is, only one degree word complement clause is possible in a sentence, independently of the number of the degree words included by the clause.
“\([{\ldots }]\) the view that a consequence relation should be paraconsistent does not entail the view that there are true contradictions. Paraconsistency is a property of an inference relation whereas dialetheism is a view about some sentences (or propositions, statements, utterances or whatever, that can be thought of as truth-bearers). The fact that one can define a non-explosive consequence relation does not mean that some sentences are true. That is, the fact that one can construct a model where a contradiction holds but not every sentence of the language holds (or, if the model theory is given intensionally, where this is the case at some world) does not mean that the contradiction is true per se. Hence paraconsistency must be distinguished from dialetheism.” (Priest and Tanaka 2009)
The choice of Rescher and Brandom’s model has been motivated by several considerations. First, our p-model of linguistic theorising—which we will introduce in Sect. 4—is partially rooted in Rescher’s approach to plausible argumentation. Therefore, the application of Rescher and Brandom’s paraconsistent logic is quite natural. Second, this logic is especially useful because it also challenges the principle of the excluded middle (which we do not discuss in this paper but which is important for other applications of the p-model). Thus it provides us with a unified treatment of deviances from two basic principles of classical logic. Third, there are several systems of paraconsistent logic, which are built on different background assumptions depending on the particular considerations motivating them. For example, according to Priest and Tanaka (2009), Tanaka et al. (2013), discussive logic (Jaśkowski 1948) intends to model discourses with differences of opinion; preservatorism (Schotch and Jennings 1980) aims at modelling information flow between mutually inconsistent but inherently consistent fragments of a theory; the basic idea of adaptive logics (Batens 2001, 2007) is that inconsistency is a relatively rare phenomenon, thus rules of inference have to be extended with a few supplementary strategies which make it possible to apply the inference rules to the “abnormalities”; logics of formal inconsistency (da Costa 1974; Carnielli et al. 2007) are a valuable endeavour to avoid isolation of inconsistency from the consistent parts of the given theory with the help of introducing metatheoretical notions of (in)consistency in the object language. Thus, it may be a reasonable option to examine in what way and to what extent different paraconsistent logics are compatible with the p-model. Nevertheless, the p-model is not compatible with every paraconsistent system. For example, Carnielli et al. 1991 semantics of translations, which aims at modelling reasoning by default, is based on assumptions that are at certain points at variance with the p-model’s interpretation of plausibility values. While Carnielli et al. stipulate that statements may be deemed definitely false on the basis of some piece of evidence but “positive evidence of trueness is not possible” (Carnielli et al. 1991: 534), the p-model enables both extremes and a continuum of intermediate values ranging from neutral plausibility to truth with certainty as well as from falsity with certainty to neutral plausibility (see Sect. 4.1 and Kertész and Rákosi 2012: 63ff.). Thus, if one decides for a paraconsistent logic which is incompatible with the p-model at the outset, then another metatheoretical model of linguistic theorising must be chosen.
See also Kertész (2004); Kertész (2012) for further applications of Rescher and Brandom’s paraconsistent logic to linguistics.
Another operation Rescher and Brandom introduce is schematisation which is intended to capture situations in which the law of the excluded middle is not valid. With respect to the treatment of inconsistency, it is only superposition that is relevant; therefore, we will not deal with schematisation.
\([A]_{w} = +\; \text{ and} \, [A]_{w} = -\) are contradictory: \(A\) either obtains in a world or not.
In Rescher and Brandom’s system there is another kind of non-standard possible world, too, in which the law of excluded middle is not valid.
Rescher and Brandom introduce ‘\(A\) is false’ as ‘\({\sim } A\) is true’. Therefore, in superposed worlds it may happen that a statement is both true and false (and in schematic worlds that it is neither true nor false).
In connection with these reconstructions, it is important to remind the reader that ‘\(A\) is true in \(w\)’ means in Rescher and Brandom’s paraconsistent logic that \(A\) obtains in the possible world \(w\); cf. (11). ‘\(A\) is false in \(w\)’ means ‘\({\sim } A\) is true in \(w\)’, that is, \({\sim } A\) obtains in this possible world.
Or to be more precise: Let the possible world \(w_{1}\) be the set of the statements related to the deep structure and \(w_{2}\) be the set of the statements related to the surface structure.
This can, of course, also be represented as
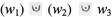
which is more intelligible in the light of (PDR).
That is, \({\sim } B\) is present in it.
Such—more or less reliable—sources are in linguistics, for example, corpora, theories, conjectures, the intuition of native speakers, experiments, fieldwork, historical documents, dictionaries, videotapes, or even inferences (cf. Rescher 1976: 6f.; Rescher 1973: 63ff., Kertész and Rákosi 2012: 63ff.).
This is usually characteristic of the first cycle(s).
Simple thick arrows indicate weak evidence for the central hypothesis of the given p-context version, while double thick arrows stand for weak evidence against it.
References
Baltin, M. R. (1987). Degree complements. In G. J. Huck & A. E. Ojeda (Eds.), Discontinuous constituency (pp. 11–26). Orlando: Academic Press.
Batens, D. (2001). A general characterization of adaptive logics. Logique et Analyse, 173–175, 45–68.
Batens, D. (2007). A universal logic approach to adaptive logics. Logica Universalis, 1, 221–242.
Carnielli, W. A., Farinas del Cerro, L., & Lima Marques, M. (1991). Contextual negations and reasoning with contradictions. (In 12th International Joint Conference on Artificial Intelligence) (pp. 532–537). Sydney: Morgan Kaufman.
Carnielli, W. A., Coniglio, M. E., & Marcos, J. (2007). Logics of formal inconsistency. In D. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (Vol. 14, pp. 15–107). Berlin: Springer.
Chomsky, N. (1980). On binding. Linguistic Inquiry, 11, 1–46.
Chomsky, N. (2002). On nature and language. Cambridge: Cambridge University Press.
da Costa, N. C. A. (1974). On the theory of inconsistent formal systems. Notre Dame Journal of Formal Logic, 15(4), 497–510.
Featherston, S. (2009). Relax, lean back, and be a linguist. Zeitschrift für Sprachwissenschaft, 28, 127–132.
Guéron, J., & May, R. (1984). Extraposition and logical form. Linguistic Inquiry, 15, 1–31.
Jaśkowski, S. (1969). [1948]). Propositional Calculus for contradictory deductive systems. Studia Logica, 24, 143–157.
Kertész, A. (2004). Philosophie der Linguistik. Studien zur naturalisierten Wissenschafts theorie. Tübingen: Narr.
Kertész, A. (2012). The ‘Galilean Style in Science’ and the inconsistency of linguistic theorising. Foundations of Science, 17, 91–108.
Kertész, A., & Rákosi, Cs. (2006). Inconsistency and plausible reasoning in an analysis of German affricates. A case study in the philosophy of linguistics. Language Sciences, 28, 386–423.
Kertész, A., & Rákosi, Cs. (2009). Cyclic vs. circular argumentation in the Conceptual Metaphor Theory. Cognitive Linguistics, 20, 703–732.
Kertész, A., & Rákosi, Cs. (2012). Data and evidence in linguistics. A plausible argumentation model. Cambridge: Cambridge University Press.
Larson, R. K. (1988). On the double object construction. Linguistic Inquiry, 19, 335–391.
Meheus, J. (Ed.). (2002a). Inconsistency in science. Dordrecht: Kluwer.
Meheus, J. (2002b). Preface. In Meheus, J. (Ed.) pp. vii–ix.
Moravcsik, E. (2006). An introduction to syntactic theory. London: Continuum.
Moravcsik, E. (2010). Conflict resolution in syntactic theory. Studies in Language, 34, 636–669.
Nickles, T. (2002). From Copernicus to Ptolemy. Inconsistency and method. In Meheus, J. (Ed.) (pp. 1–33).
Polya, G. (1948). How to solve it. Princeton: Princeton University Press.
Polya, G. (1954). Patterns of plausible inference. London: Oxford University Press.
Priest, G. (2001). Paraconsistent belief revision. Theoria, 67(3), 214–228.
Priest, G. (2002a). Inconsistency and the empirical sciences. In Meheus J. (Ed.), (pp. 119–128).
Priest, G. (2002b). Paraconsistent logic. In D. Gabbay & F. Guenthner (Eds.), Handbook of paraconsistent logic (pp. 287–393). Dordrecht: Kluwer.
Priest, G., Beall, J. C., & Armour-Garb, B. (Eds.). (2004). The law of non-contradiction. Oxford: Clarendon Press.
Priest, G. & Tanaka, K. (2009). Paraconsistent logic. In The Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/logic-paraconsistent/ (accessed 04. 09. 2012)
Rescher, N. (1964). Hypothetical reasoning. Amsterdam: North-Holland.
Rescher, N. (1973). The coherence theory of truth. Oxford: Clarendon Press.
Rescher, N. (1976). Plausible reasoning. Assen & Amsterdam: Van Gorcum.
Rescher, N. (1987). How serious a fallacy is inconsistency? Argumentation, 1, 303–316.
Rescher, N., & Brandom, R. (1980). The logic of inconsistency. Oxford: Blackwell.
Ross, J. R. (1967). Constraints on variables in syntax. Bloomington: Indiana University Linguistics Club.
Schütze, C. T. (1996). The empirical base of linguistics. Grammaticality judgments and linguistic methodology. Chicago: The University of Chicago Press.
Schotch, P. K., & Jennings, R. E. (1980). Inference and necessity. Journal of Philosophical Logic, 9, 327–340.
Tanaka, K., Berto, F., Mares, E., & Paoli, F. (2013). Paraconsistency: Introduction. In K. Tanaka, F. Berto, E. Mares, & F. Paoli (Eds.), Paraconsistency: Logic and applications (pp. 1–12). Dordrecht: Springer.
White, J. R. (1997). Result clauses and the structure of degree phrases. UCL Working Papers in Linguistics, 9, 1–20.
Acknowledgments
Work on the present paper was supported by the MTA-DE Research Group for Theoretical Linguistics and the project OTKA K 77823. Csilla Rákosi’s work was also supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kertész, A., Rákosi, C. Paraconsistency and Plausible Argumentation in Generative Grammar: A Case Study. J of Log Lang and Inf 22, 195–230 (2013). https://doi.org/10.1007/s10849-013-9171-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-013-9171-y