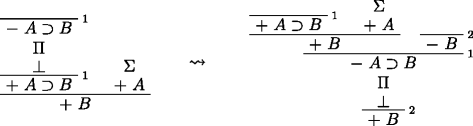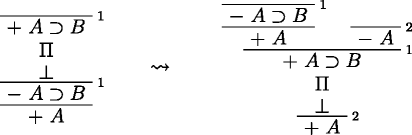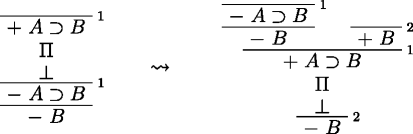Some Comments on Ian Rumfitt’s Bilateralism

Abstract

Ian Rumfitt has proposed systems of bilateral logic for primitive speech acts of assertion and denial, with the purpose of ‘exploring the possibility of specifying the classically intended senses for the connectives in terms of their deductive use’ (Rumfitt Mind 109, 781–823 (4): 810f). Rumfitt formalises two systems of bilateral logic and gives two arguments for their classical nature. I assess both arguments and conclude that only one system satisfies the meaning-theoretical requirements Rumfitt imposes in his arguments. I then formalise an intuitionist system of bilateral logic which also meets those requirements. Thus Rumfitt cannot claim that only classical bilateral rules of inference succeed in imparting a coherent sense onto the connectives. My system can be extended to classical logic by adding the intuitionistically unacceptable half of a structural rule Rumfitt uses to codify the relation between assertion and denial. Thus there is a clear sense in which, in the bilateral framework, the difference between classicism and intuitionism is not one of the rules of inference governing negation, but rather one of the relation between assertion and denial.

Appendix: Formal Results

1.1 Smiley can be restricted to Atomic Premises in $\mathfrak {AD}+\text {Smiley}$

The proof uses only +¬E, −¬E, +& E, −& E, +∨E, −∨E, +⊃E, −⊃E.Case 1. Negation. The deduction on the right can be transformed into the deduction on the left:

Case 2. Conjunction. Where C is an arbitrary atomic formula, the deduction on top can be transformed into the deduction below:

Case 3. Disjunction. The deduction on top can be transformed into the deduction below, where C is an arbitrary atomic formula:

Case 4. Implication. The deduction on the left can be transformed into the deduction on the right:

1.2 Normalisation in $\mathfrak {I}$

Let a maximal formula of a deduction in $\mathfrak {I}$ be one that is the major premise of an elimination rule for its main connective and either the conclusion of an introduction rule for its main connective or the conclusion of Reductio. In the following, I will specify procedures for removing maximal formulas from deductions. In each case, it suffices to consider deductions which end with an application of a rule creating a maximal formula. A suitable induction over the complexity of deductions shows that any maximal formula can be removed from deductions in $\mathfrak {I}$. For instance, call the degree of a formula the number of connectives occurring in it, and call the degree of a deduction the sum the degrees of its maximal formulas. Applying the reduction procedures to the left most and upper most maximal formula of a deduction will reduce its degree. Continuing in the same way will eventually produce a deduction in normal form, in which there are no maximal formulas.

Case 1. Conjunction. We need to consider only two cases. The obvious reduction procedure takes care of the case where +& I is followed immediately by +& E. The case where +& E is preceded by Reductio is dealt with by replacing the deduction on the left with the deduction on the right:

If the conclusion + A is subject to an elimination rule, the reduction procedure may introduce a new maximal formula, but one that is of lower degree than the one removed. The case for the other elimination rule of +& is similar.

Case 2. Disjunction. We need to consider only two cases. The obvious reduction procedure takes care of the case where −∨I is followed immediately by −∨E. The case where −∨E is preceded by Reductio is dealt with by replacing the deduction on the left with the deduction on the right:

If the conclusion − A is subject to an elimination rule, the reduction procedure may introduce a new maximal formula, but one that is of lower degree than the one removed. The case for the other elimination rule of −∨ is similar.

Case 3. Negation. We need to consider only one case, which is dealt with by replacing the deduction on the left with the deduction on the right:

If the conclusion − A is subject to an elimination rule, the reduction procedure may introduce a new maximal formula, but one that is of lower degree than the one removed.

Case 4. Implication. We need to consider three cases, corresponding to the three elimination rules for ⊃:

• i)

  

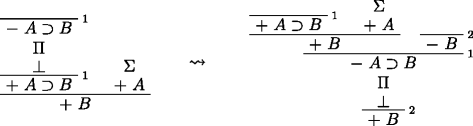
• ii)

  

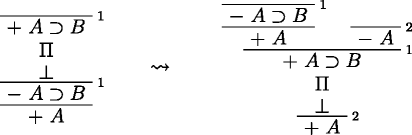
• iii)

  

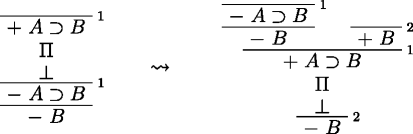
If the conclusions + A, + B and −B are subject to an elimination rule, the reduction procedure may introduce a new maximal formula, but one that is of lower degree than the one removed.

Applying the reduction procedures for ⊃ may introduce maximal formulas of the same degree as the one removed at the top of the deduction π, if + A⊃B was the premise of an elimination rule. For each possibility, however, the formula can be removed trivially, so that any maximal formula that might arise is then of lower complexity than the one removed.

In case i), if − A⊃B is major premise of an elimination rule, the conclusion is either + A or − B. In the former case, move Σ on top of + A and delete the rest. In the other case, delete everything above that conclusion and discharge it when applying Smiley to the conclusion ⊥ of π.

If + A⊃B is major premise of an elimination rule, its conclusion is + B and there is a deduction Σ of the minor premise + A. In case ii), as the minor premise of the rule is identical to the conclusion of the whole deduction, move Σ on top of it and delete everything else. In case iii), delete everything on top of the conclusion + B of the rule and discharge it with the final application of Reductio.

1.3 Properties of $\mathfrak {Int}$-$\mathfrak {B}$

1.3.1 Restrictions to Atomic Premises

• 1. Intuitionist Smiley can be reduced to atomic premises α. The proof appeals in the induction step to ex contradictione quodlibet, −¬E and the first −⊃E restricted to atomic conclusions.

• 2. Ex contradictione quodlibet can be restricted to atomic premises. The proof is obvious. It only needs the induction hypothesis in the steps for conjunctive and disjunctive premises. The step for + A⊃B,− A⊃B⊩β appeals to Intuitionist Smiley, with premises + B, − B and conclusion − A, discharging + A.

• 3. It follows immediately that α can be restricted to atomics in −⊃I and −¬I.

1.3.2 Restrictions to Atomic Conclusions

• 1. Ex falso quodlibet can be restricted to atomic conclusions. The proof is obvious.

• 2. The same constructions show that the first −⊃I rule and −¬E can be restricted to atomic conclusions.

• 3. Intuitionist Smiley can be restricted to atomic conclusions. The proof appeals to ex contradictione quodlibet in the step for ⊃, to derive the premise + A⊃B.

1.3.3 The Rules are Harmonious in Tennant’s Sense

I’ll only show this for the rejective implication and conjunction rules and leave negation to the reader.

1.a):

Given −⊃I, − A⊃B is the weakest speech act that can be eliminated by −⊃E. Suppose some speech act ϕ satisfies the conditions specified for the major premise in the rules for −⊃E, i.e. for arbitrary C, ϕ,− A⊩− C, ϕ,− A⊩+ C and ϕ⊩− B. Then by −⊃I, ϕ⊩− A⊃B.

1.b):

Given −⊃E, − A⊃B is the strongest speech act that can be introduced by −⊃I. Suppose some speech act ϕ satisfies the condition specified for the conclusion of the introduction rule for −⊃, i.e. if Γ,− A⊩− C, Γ,− A⊩+ C and Γ⊩− B, then Γ⊩ϕ. By −⊃E, − A⊃B,− A⊩− C, − A⊃B,− A⊩+ C and − A⊃B⊩− B. Hence by assumption − A⊃B⊩ϕ.

2.a):

Given −& I, − A&B is the weakest speech act that can be eliminated by −& E. Suppose some speech act ϕ satisfies the conditions specified for the major premise in −& E, i.e. ϕ,+ A⊩− B. Then by −& I, ϕ⊩− A&B.

2.b):

Given −& E, − A&B is the strongest speech act that can be introduced by −& I. Suppose some speech act ϕ satisfies the condition specified for the conclusion of the introduction rule of −&, i.e. if Γ,+ A⊩− B, then Γ⊩− A&B. By −& E, − A&B,+ A⊩− B. Hence by assumption − A&B⊩ϕ.

1.3.4 Adding the Classical Half of Smiley

The premises of the classical half of Smiley can be restricted to atomics when added to $\mathfrak {Int}$-$\mathfrak {B}$. We only need to consider the cases of &, ⊃ and ¬, the rules for ∨ being as in $\mathfrak {B}$. Case 1. Conjunction. The deduction on the left can be transformed into the deduction on the right:

Case 2. Implication. Where D is an arbitrary atomic formula, the deduction on top can be transformed into the deduction below:

Case 3. Negation. Where D is an atomic formula, the deduction on the left can be transformed into the deduction on the right: