Fluids, Molecules and Paradoxes of Infinity

Abstract

Several paradoxes of infinity have recently featured in this journal involving gases distributed in a denumerable infinite series of compartments. I shall demonstrate in this paper that:

a) None of these new paradoxes applies where the gases comply with both Boyle’s law and Avogadro’s law. As several of these new paradoxes expressly require compliance with Boyle’s law, it is unclear, in principle, as to whether there is a plausible model of gas that is able to uphold them all.

b) Notwithstanding a), any of the above paradoxes (and their variations) can be reinstated by acknowledging (contrary to what is widely assumed in the literature) that there are two distinct, non-equivalent concepts of ideal gas. Indeed, the various infinity puzzles actually enable a distinction to be made between the two concepts (which is a particularly elegant way of doing so).

1 Introduction: Static Paradoxes and Paradoxes of Equilibrium

Two different kinds of new paradoxes of infinity have recently been proposed (Laraudogoitia 2020a, 2020b). What they have in common is their formulation in terms of gases enclosed in a denumerable infinity of compartments connected to one another. However, the nature of both kinds of paradoxes is different. In this first section, I will simply present them succinctly in order to pave the way for further discussion. Having demonstrated their incompatibility with the conjunction of Boyle’s law and Avogadro’s law in Sect. 2 (and presented some simple variations in Sect. 3), in Sect. 4 I will argue that there is no plausible kinetic model of gas under which all the paradoxes mentioned can be formulated. Meaning that, even though they can be formally derived, we have no clear idea of what the nature of a gas may be for such a thing to be possible. From the viewpoint of some philosophers (those who consider only “minimally” realistic models to be of value), this may seem to be an argument against its philosophical interest given, in principle, the purely formal character of its derivation. Section 5 then shows that philosophical interest does not suffer because, after all, there is a simple way of presenting all the paradoxes as paradoxes involving the concept of ideal gas as a strictly continuous medium.

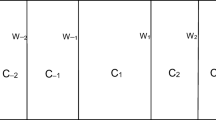
On the basis of Laraudogoitia’s terminology, I will distinguish between static paradoxes and equilibrium paradoxes. In static paradoxes, what we have in essence is a finite, rigid, hollow cylinder, C, divided into a denumerable infinite series of compartments C_i (C₁, C₂, C₃, …, C_n, … ) of volumes V(C_i) and filled with gas at the respective pressures p(C_i). Adjacent compartments are separated by D_i pistons which remain fixed inside C due to the frictional force exerted on their inner side surface. It is assumed that this frictional force is bounded by a given maximum finite k* value. In all cases, series Σ V(C_i ) is clearly convergent and cylinder C is at rest. Paradoxes arise for certain pressure distribution values p(C_i), which are as follows: the net force that the gases and pistons inside C exert on C is not null, contradicting the fact that C is (and must be) at rest. Not all pressure distributions are paradoxical. In order to illustrate this, Laraudogoitia 2020a distinguishes between a non problematic reference case (the net force on C of gases and pistons situated in its interior is null, as it should be) and five representative paradoxes. The pressures in each circumstance are as follows:

Reference case 0: p(C_i ) = 1/i (i > 0).

Paradox 1: p(C_i) = 1 + (1/i) = (i+1)/i (i > 0).

Paradox 2: p(C_i) = 1 (i > 0).

Paradox 3: p(C_i) = 1/1 − 1/2 + 1/3 − 1/4 + … + (− 1)ⁱ⁺¹/i (i > 0).

Paradox 4: p(C_i) = i/(i + 1) = 1 − (1/(i +1)) (i > 0).

Paradox 5: p(C_2i−1) = 1 but p(C_2i) = 0 (i > 0).

Moving on to the second type of paradoxes, for the purposes of this paper, the essence of equilibrium paradoxes can be described in the following terms. There are two cases. In the first, as before, cylinder C contains a denumerable infinity of compartments C_i. But with the following differences: the ordinal type of C_i is ω* + ω (specifically …, C_−n, …, C₋₃, C₋₂, C₋₁, C₁, C₂, C₃, …, C_n, … ) and pistons D_i can move frictionlessly inside C. The second case is altogether the same as the first except for the fact that C is a hollow toroid divided into the denumerable infinity of compartments C_i with the usual ordinal type ω (namely, C₁, C₂, C₃, …, C_n, … ). Paradoxes now arise for certain values of the initial pressures and volumes (Pº(C_i) y Vº(C_i) respectively), which are as follows: in the state of final equilibrium (where pressures in all compartments are equal) the volume occupied by each gas is null, indicating that it is at infinite pressure (i.e., in final equilibrium the gases are squeezed inside C occupying null volume and subjected to infinite pressure). Not all initial conditions (initial pressures and volumes) lead to such a paradoxical final equilibrium. In order to illustrate this, Laraudogoitia 2020b distinguishes two non problematic reference cases (in final equilibrium all gases experience the same common finite pressure, so their final volumes are also finite, filling the inside of C) and two representative paradoxes. The initial conditions (pressures and volumes) in each circumstance are as follows:

Reference case 1: Pº(C_i) = ⎜1/i⎜ and Vº(C_i) = 1/i² (i ≠ 0) (Hollow cylinder).

Reference case 2: Pº(C_i) = ⎜i⎜ and Vº(C_i) = ⎜1/i³⎜(i ≠ 0) (Hollow cylinder).

Paradox I: Pº(C_i) = ⎜i⎜ and Vº(C_i) = 1/i² (i ≠ 0) (Hollow cylinder).

Paradox II: Pº(C_i) = i and Vº(C_i) = 1/i² (i > 0) (Hollow toroid).

In the following sections we will look into the conditions under which static paradoxes and equilibrium paradoxes are possible.

2 Under the Avogadro-Boyle Tandem, neither Static Paradoxes nor Equilibrium Paradoxes are Possible

If we are looking for a theoretical model of gas where static paradoxes and equilibrium paradoxes are both formulable, such a model must undoubtedly presuppose Boyle’s law (at constant temperature, the product of pressure by the volume of a given mass of gas is constant). The reason for this is that this law is used to address both reference cases 1 and 2 and, above all, paradoxes I and II mentioned in the previous section (equilibrium paradoxes). Is there anything additional interesting to say about the theoretical model of gas being sought? We will now see a significant negative result: gas cannot fulfill Avogadro’s law. In its most appropriate standard formulation, this law states as follows: at a given temperature and pressure, equal volumes of gas contain equal numbers of molecules.¹ We shall present our negative result in the form of a theorem:

Theorem 1

According to Boyle’s law and Avogadro’s law, neither reference cases, nor static paradoxes, nor equilibrium paradoxes are possible.

Proof

We should first remember that in the reference cases, static paradoxes and equilibrium paradoxes, temperature does not play an essential role: it is supposed to remain constant at all times (typically, due to the contact of gases with a thermal reservoir at that temperature through diathermal walls). In reference case 0 and static paradoxes, it must be lim_{i → ∞}V(C_i) = 0 (due to the convergence of Σ V(C_i )) and since p(C_i) has an upper bound, lim_{i → ∞}p(C_i)V(C_i) = 0 is fulfilled. In reference cases 1 and 2 and equilibrium paradoxes, it also follows that lim_{i → ∞}Vº(C_i) = 0 and lim_{i → ∞}Pº(C_i)Vº(C_i) = 0. For the sake of economy, my reasoning below only uses initial values Pº(C_i) and Vº(C_i) in the context of equilibrium paradoxes, but identical arguments will apply to permanent values p(C_i) and V(C_i) in the context of static paradoxes. Let us suppose that the gas in compartment C₁ (at initial pressure Pº(C₁)) was subjected, with no change in temperature, to the new pressure Pº(C_k) (identical to the initial pressure in compartment C_k). Its volume would then take a given value V*(C_k). The number of molecules in the gas would not vary in the process, but (according to Boyle’s law) Pº(C₁)Vº(C₁) = 1/H (constant) = Pº(C_k)V*(C_k), V*(C_k) = 1/[HPº(C_k)] = [Vº(C_k)/(HPº(C_k) Vº(C_k))] and, finally, Vº(C_k)/ V*(C_k) = HPº(C_k)Vº(C_k) would be obtained. As lim_{i → ∞}Pº(C_i)Vº(C_i) = 0, Vº(C_k) is (at pressure Pº(C_k)) a progressively smaller fraction (tending to zero with growing k) of V*(C_k). According to Avogadro’s law, in Vº(C_k) there is (at pressure Pº(C_k)) a progressively smaller fraction (tending to zero with growing k) of the quantity of molecules in V*(C_k). But in V*(C_k) there is (at pressure Pº(C_k)) the same quantity of molecules as in Vº(C₁) (at pressure Pº(C₁)). Therefore, in Vº(C_k) there is (at pressure Pº(C_k)) a progressively smaller fraction (tending to zero with growing k) of the quantity of molecules in Vº(C₁) at pressure Pº(C₁). As the number of molecules initially in compartment C₁ of volume Vº(C₁) is (reasonably) finite, it follows that, for sufficiently large k, the number of molecules in Vº(C_k) (at pressure Pº(C_k)) is lower than the unit. This absurdity indicates that the assumed initial state in reference cases 1 and 2, as well as in equilibrium paradoxes (and the same can obviously be said for reference case 0 and static paradoxes), is not physically possible (in the sense that it is incompatible with the assumed conjunction of Boyle’s law and Avogadro’s law). In other words, under the assumed conditions only a finite number of compartments can contain gas molecules at constant defined pressure. The rest may be, for example, empty compartments. It is not the case that there is a defined positive integer k from which compartments C_i (i > k) must be empty ², so that those with an index lower than or equal to k are filled. Rather, what occurs is that when the C_i are sufficiently small, there will be (if indeed there are any) so few molecules inside that we cannot speak of pressure (at least not of constant pressure), and the content of Boyle’s law (no longer strictly applicable) is blurred. This is the path along which all paradoxes disappear (and even reference cases are no longer possible, even though they do not lead to paradox as such).

The impossibilities revealed in theorem 1 can now be seen succinctly and elegantly as a consequence of the following theorem:

Theorem 2

Assuming Avogadro’s law, the constant in Boyle’s law for a given mass of gas is proportional to the number of molecules in the mass of gas, the proportionality constant being independent of its nature.

Proof

Whether it be a given mass of gas under pressure P and occupying volume V, we know that PV = K (constant). As this constant depends in some way on gas mass, it is clear that K is a function of number of molecules N, K = f(N). We know that fraction α of the number of molecules N will be found in fraction α of V. Since PαV = αK = f(αN), it follows that f(αN) = αf(N). So, it is clear that function f(N) is linear. Therefore, the constant in Boyle’s law for a given mass of gas is proportional to the number of gas molecules in that mass: K = δN. Avogadro’s law therefore ensures that the constant δ is the same for all gases. So, in general, PV = δN.

Indeed, we know that in reference case 0 and static paradoxes, lim_{i → ∞}p(C_i)V(C_i) = 0, and that in reference cases 1 and 2 and equilibrium paradoxes, lim_{i → ∞}Pº(C_i)Vº(C_i) = 0. By using N_i to denote the number of molecules in compartment C_i, lim_{i → ∞} δN_i = 0 = δ lim_{i → ∞} N_i is obtained in each of these situations. Thus lim_{i → ∞} N_i = 0, which is absurd (as it would oblige an infinity of compartments to have a number of molecules lower than 1) unless it is concluded that an infinite number of compartments must actually be empty; counter to the assumption made when formulating the infinity puzzles.

Also, Laraudogoitia (2020b) very briefly mentions a possible criticism of his paradoxes based on the atomic nature of matter. However, he sets this aside by stating that “Such criticism is misguided. Paradoxes of infinity are essentially theoretical-conceptual, not empirical, problems”. This approach is clearly insufficient in light of the results obtained in this section. Indeed, even if the paradoxes of infinity are theoretical-conceptual, the above theorems show that they can be avoided by simply resorting to Boyle’s and Avogadro’s laws, without engaging in any considerations whatsoever concerning the effective reproducibility in the real world of such paradoxical configurations (i.e., without resorting to the obvious empirical limitations to realizing infinitude). In other words, if a gas fulfills Boyle’s and Avogadro’s laws, it cannot therefore fill all the compartments it is supposed to occupy in Laraudogoitia’s paradoxes (2020a, b). Indeed, as has been seen, under the conditions of such paradoxes all the compartments, save a finite number of them, should be empty: there are no infinity puzzles as such.

3 Under the Avogadro-Boyle Tandem, There are New Equilibrium Paradoxes

Based on theorem 2 in the previous section and its demonstration, it follows that (assuming only Boyle’s law and Avogadro’s law) the paradoxes of infinity that interest us in this paper are only possible when there are masses of gas (under pressure p_k and occupying volumes v_k) whose constants in Boyle’s law (p_k⋅ v_k) do not tend to zero when k → ∞. By following this idea, we will first see that, despite everything, a multitude of trivial variants of equilibrium paradoxes are finally possible (meaning compatible with both Boyle’s law and Avogadro’s law). I use the nomenclature introduced for them in Sect. 1, and distinguish the hollow cylinder case from the hollow toroid case in the same clear way. This last distinction is of no importance at this time, but will help the overall nature of the variation proposed to be clearly seen by comparing it with the original version:

Paradox I*: Pº(C_i) = ⎜i⎜^1+β and Vº(C_i) = 1/⎜i⎜^1+α (i ≠ 0, β ≥ α > 0) (Hollow cylinder).

Paradox II*: Pº(C_i) = i^1+β and Vº(C_i) = 1/i^1+α (i > 0, β ≥ α > 0) (Hollow toroid).

Consider I* (analogously applies to II*). For the details that follow, familiarity with the detailed argument leading to the original equilibrium paradoxes (introduced briefly at the end of Sect. 1) is advisable. With Vº(C_i) = 1/⎜i⎜^1+α (α > 0), we are assuming that the finite interior volume of C is V = ∑(1/⎜i⎜^1+α), that is, finite. As always, the temperature of the total system remains constant while pistons D_i are released in order to go to the state of equilibrium (in which all the pressures of the compartments are identical). These final pressures being P(C_i) = P, and V(C_i) the final volumes. So, Boyle’s law requires that, for each i, Pº(C_i)Vº(C_i) = P(C_i)V(C_i), that is, ⎜i⎜^β−α = PV(C_i). Hence, V(C_i) = (1/P)⎜i⎜^β−α. However, this result is paradoxical. In effect, the final volume of the gases is ∑V(C_i) = (1/P)∑⎜i⎜^β−α and series ∑⎜i⎜^β−α diverges to infinity because β ≥ α. As the gases in final equilibrium cannot occupy a volume larger than V (the volume of rigid cylinder C’s internal hollow), the only possibility is that 1 / P = 0, that is to say, the final pressure shared by all the gases in equilibrium is infinite. From V(C_i) = (1/P)⎜i⎜^β−α, it therefore follows that the final volume of each gas is zero. The consequence being that in no way can ∑Vº(C_i) = ∑V(C_i) be fulfilled because the total final volume of the gases must also be zero. The gases “squeeze together” inside C at infinite pressure and occupy no volume.

Unfortunately, the conditions making equilibrium paradoxes effectively possible prevent the possibility of static paradoxes. Indeed, if (as previously seen) lim_k→∞(p_k⋅ v_k) ≠ 0 is necessary, given that static paradoxes require lim_{i → ∞}V(C_i) = 0, lim_{i → ∞}p(C_i) = ∞ must therefore also be fulfilled. However, since V(C_i) must decrease more rapidly than α/i, no matter what constant α is (in order for Σ V(C_i ) to be finite), p(C_i) must also grow faster than (1/α)i. Meaning that the pressure difference between two contiguous cylinder C compartments cannot be bounded ³ The outcome is that the net force that the gases in C_i+1 and C_i exert on the D_i piston separating them grows limitlessly. Since static paradox conditions require the D_i to remain fixed within C, the frictional force between each of them and the cylinder’s inner side surface must also grow limitlessly (nonetheless, in order to compensate for the force originating in the pressure difference, it has to point in the opposite direction). But this is impossible because (as mentioned in Sect. 1) it is always assumed that this frictional force is bounded by a given finite value k*.

4 An Opaque Model of Gas

The considerations in the previous sections show that, while a gas must comply with Boyle’s law in order to formulate equilibrium paradoxes (and may also fulfill Avogadro’s law in some equilibrium paradoxes, such as I* and II*), it must violate Avogadro’s law in order to allow for static paradoxes. Is there a kinetic molecular model of gas where both types of paradoxes are possible at the same time? It must be taken into account, for instance, that an ideal gas complies with Boyle’s law but also fulfills Avogadro’s law. At the other extreme, more realistic models of gas do not strictly fulfill either of the laws. What this seems to imply is that, even though all the above paradoxes may be derived jointly in a purely formal manner, we have no clear idea of what the nature may be of a gas for such a thing to be possible. This situation evokes an episode in the history of “mechanical philosophy” that may be worth remembering. As several authors have convincingly argued (e.g. Clericuzio 2000), the explicit ontological reduction program in Boyle’s philosophy failed to achieve any significant success throughout the seventeenth century. The elasticity of gases was taken as an “intermediate cause” to account for their behavior both in expansion (different to solid bodies in this regard) and contraction. Analysis of Boyle’s law remained at this level. Chalmers (2017, p. 185) puts it clearly: “Boyle explicitly made the point that he was to characterize and appeal to spring while not explaining it at the corpuscular level. Boyle made the point that experimental science could and should proceed by appeal to unexplained causes as weight and elasticity in …” In our case, all that can be said at this time is that static and equilibrium paradoxes manifest themselves together in gases considered elastic fluids under Boyle’s law. Our ignorance of a fluid’s “ultimate structure” with such characteristics is assumed. I shall therefore use the term “opaque model” of gas.

5 Infinity Puzzles and Two Concepts of Ideal Gas

Consider the general equation of state for ideal gases PV = nRT, where R is the universal ideal gas constant. This has are two readings, the reductionist reading and phenomenological reading. The difference lies in the way of considering the number of moles, n. In the usual reductionist way (usual among physicists and philosophers of physics), n is taken as the quotient between the number N of gas molecules present and the Avogadro number of molecules (N_A = 6.0225⋅10²³). Thus, n = N/N_A. So, the equation of state can be set as PV = NkT,⁴ where k = R/ N_A is Boltzmann’s universal constant.

Alternatively, the reading I call phenomenological is found largely in engineering-oriented publications (e.g., Moran & Shapiro 2000). Here n = a/M is taken, where a is the mass of gas and M its molecular weight. By introducing the non-universal constant R* = R/M, whose value already depends on the gas considered, the equation of state is PV = aR*T. Now the atomic structure of matter does not appear explicitly in any way. Taking R* as a primitive constant characteristic of each gas, the equation PV = aR*T adapts perfectly to the opaque model of gas mentioned above. By taking this additional step, with this interpretation of R* as a primitive constant, the atomic structure of the gas does not even appear implicitly, and even Avogadro’s law no longer makes sense. Our ignorance of a gas’s “ultimate structure” means that it is now modelized as a strictly continuous medium (a field of matter defined at each point it occupies in space by its density, pressure and temperature) characterized by a parameter R* which, unlike k, is not a universal constant. It is precisely this non-universality of R* that warrants mention of our ignorance of the “ultimate structure” and of the “opaque model” of ideal gas. In the strict context of such an opaque model, each value of R* would be an ontologically brute fact⁵. It follows from the above that, under given pressure and temperature conditions, it is possible to occupy an arbitrarily small volume of space with a sufficiently small mass of gas. For any ε > 0, however small, it is possible to have a finite mass of gas such that PV/T < ε. As we know, this is all that is needed for the static and equilibrium paradoxes in Sect. 1 to be possible, in accordance with the gas model’s opaque character.

In contrast, the explicit reductionism of PV = NkT prevents something similar. Under given pressure and temperature conditions, it is not possible to occupy an arbitrarily small volume with gas made up of molecules (N cannot be lower than the unit). It is not possible to have an aggregate of particles in P, V and T conditions in such a way that PV/T < k (Boltzmann’s constant). This certainly avoids the static and equilibrium paradoxes in Sect. 1. It should nonetheless be noted that the kinetic molecular model of ideal gas is not problem-free. It is not free, for instance, from the equilibrium paradoxes seen in Sect. 3.

6 Conclusion and Perspectives

We have seen how static paradoxes 1 to 5 and equilibrium paradoxes I and II disappear when an ideal gas considered to be a continuous medium (what I term an “opaque model” of ideal gas) is replaced by an ideal gas made up of mechanical particles, that is, of molecules (kinetic model of ideal gas). In this sense, the aforementioned paradoxes seem to be an interesting theoretical resource in order to distinguish both models of ideal gas in a highly non-trivial way. Two models whose vastly different character did not seem to arouse the interest of philosophers until today. The new infinity puzzles may perhaps help to remedy this state of affairs. To date, no philosophical study of the ideal gas law has been conducted. A wealth of scientific-technical and historical literature can be found about it but scarcely any philosophical literature (beyond that relating it very loosely to the Gibbs paradox). This contrasts with the multiplicity of details with which philosophers have approached other basic constructs in classical physics, such as mechanical particles and Newtonian laws describing their behavior. By means of the paradoxes considered in detail in this paper (which involve infinite ideal gas systems), this situation can also be expected to change in the future. Ultimately, the equilibrium paradoxes introduced in Laraudogoiria (2020b) can be considered, from a fairly natural point of view, thermodynamic analogues⁶ (particularly simple, as only mechanical equilibrium is non-trivially involved, and not thermal equilibrium or chemical equilibrium) of the dynamical supertasks already extensively studied in the classical mechanics of infinite particle systems (see Manchak & Roberts 2016 for relevant references). The true scope of this analogy must be decided by an investigation that has yet to be carried out.