On the Epistemic Foundation for Iterated Weak Dominance: An Analysis in a Logic of Individual and Collective attitudes

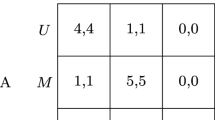
Abstract

This paper proposes a logical framework for representing static and dynamic properties of different kinds of individual and collective attitudes. A complete axiomatization as well as a decidability result for the logic are given. The logic is applied to game theory by providing a formal analysis of the epistemic conditions of iterated deletion of weakly dominated strategies (IDWDS), or iterated weak dominance for short. The main difference between the analysis of the epistemic conditions of iterated weak dominance given in this paper and other analysis is that we use a semi-qualitative approach to uncertainty based on the notion of plausibility first introduced by Spohn, whereas other analysis are based on a quantitative representation of uncertainty in terms of probabilities.

Appendix: Some Proofs

1.1 A.1 Proof of Theorem 1

Satisfiability in PDL-A is decidable.

Proof

First of all note that the logic PDL-A ⁻⁻ is nothing but the variant of PDL where each atomic knowledge program i is interpreted by an equivalence relation ℰ _i . This logic can be embedded into PDL extended with converse, by simulating every atomic knowledge programs i with a composite program $(a \cup a^{-1})^{\ast }$, where a is an arbitrary atomic program interpreted by a binary relation $\mathcal {R}_{a}$ (not necessarily an equivalence relation!) and $a^{-1}$ is the converse of a. PDL with converse is decidable [33]. It follows that PDL-A ⁻⁻ is decidable too.

Moreover, note that the problem of satisfiability in PDL-A ⁻ is reducible to the problem of global logical consequence in PDL-A ⁻⁻, where the special atoms $\mathsf {exc}_{i,\mathsf {h}}$ are just elements of the set of propositional variables Prop and the set of global axioms Γ is the set of all formulas of Proposition 13. That is, we have $\models _{\textsf {PDL-A}^{-}}\varphi$ if and only if $\Gamma \models _{\textsf {PDL-A}^{--}}\varphi$. Observe that Γ is finite (because Num is finite). It is a routine task to verify that the problem of global logical consequence in PDL-A ⁻⁻ with a finite number of global axioms is reducible to the problem of satisfiability in PDL-A ⁻⁻. In particular, if $\Gamma = \{\chi _{1}, \ldots , \chi _{n} \}$, we have $\Gamma \models _{\textsf {PDL-A}^{--}}\varphi$ if and only if $\models _{\textsf {PDL-A}^{--}} \mathsf {CK}_{Agt} (\chi _{1} \wedge \ldots \wedge \chi _n) \rightarrow \varphi$, where $\mathsf {CK}_{Agt}$ is the common knowledge operator defined in Section 4.2. As the problem of satisfiability checking in PDL-A ⁻⁻ is decidable, it follows that the problem of satisfiability checking in the logic PDL-A ⁻ is decidable too.

Proposition 15 ensures that red provides an effective procedure for reducing a PDL-A formula φ into an equivalent PDL-A ⁻ formula $red(\varphi )$. As PDL-A ⁻ is decidable, PDL-A is decidable too. □

1.2 A.2 Proof of Theorem 4

Let $s\not \in S^{DWDS^{1}-IDSDS}$. Then:

$$\models \mathsf{CBel}_{Agt} \mathsf{AllPRat}_{Agt}\rightarrow \neg pl(s) $$

Proof

The proof is by induction.

Base case  For all $s\not \in S_{1}^{DWDS^{1}-IDSDS}$ we prove that:

(A1) $\models \mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}\rightarrow \neg pl(s)$

To prove (A1), it is sufficient to prove the following validity (B1), as $\mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}\rightarrow \mathsf {AllPRat}_{Agt}$ is valid by the item (10f) in Proposition 17.¹⁹ For all $s\not \in S_{1}^{DWDS^{1}-IDSDS}$ we have that:

(B1) $\models \mathsf {AllPRat}_{Agt}\rightarrow \neg pl(s)$

And to prove (B1), it is sufficient to prove that if $s[i]\not \in S_{i, 1}^{DWDS^{1}-IDSDS}$ then:

(C1) $\models \mathsf {PRat}_{i}\rightarrow \neg pl_{i}(s[i])$

Let us prove (C1) by reductio ad absurdum. We assume that $s[i] \not \in S_{i, 1}^{DWDS^{1}-IDSDS}$ and $M,w \models \mathsf {PRat}_{i}$ and $M,w \models pl_{i} (s[i])$for some arbitrary model M and world w in M. We are going to show that these three facts are inconsistent. $s[i]\not \in S_{i,1}^{DWDS^{1}-IDSDS}$ implies that:

(D1) there is $b_{i}\in S_{i}$ such that: (1) for all $s_{-i}^{\prime }\in S_{-i}$ we have $\langle s[i],s_{-i}^{\prime }\rangle \leq _{i} \langle b_{i}, s_{-i}^{\prime }\rangle$ and (2) there is $s_{-i}^{\prime \prime }\in S_{-i}$ such that $\langle s[i],s_{-i}^{\prime \prime }\rangle <_{i} \langle b_{i},s_{-i}^{\prime \prime } \rangle$.

$M,w \models \mathsf {PRat}_{i}$ and $M,w \models pl_{i}(s[i])$ together imply:

(E1) $M,w \models \mathsf {PRat}_{i}(s[i])$.

By the Constraint (Constr3), (D1) implies that:

(F1) there is $b_{i} \in S_{i}$ such that: (1) for all $s_{-i}^{\prime } \in S_{-i}$ we have $\langle s[i],s_{-i}^{\prime }\rangle \leq _{i}\langle b_{i}, s_{-i}^{\prime }\rangle$ and (2) there are $s_{-i}^{\prime \prime }\in \mathit {S}_{-i}$ and $u \in W$ and $\mathsf {h} \in Num$ such that $(w,u) \in \mathcal {E}_{i}$ and $\boldsymbol {\mathit {A}}_{-i}(u)=s_{-i}^{\prime \prime }$ and $\kappa (u,i) = \mathsf {h}$ and $\langle s[i],s_{-i}^{\prime }\rangle <_{i}\langle b_{i},s_{-i}^{\prime \prime }\rangle$.

(F1) implies that:

(G1) $M,w \not \models \mathsf {PRat}_{i}(s[i])$.

But (G1) and (E1) are in contradiction.

Inductive case  For m > 1, we assume that if $s\not \in S_{m}^{DWDS^{1}-IDSDS}$ then:

• (Inductive Hypothesis) $\models \mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}\rightarrow \neg pl(s)$

We are going to prove that if $s\not \in S_{m+1}^{DWDS^{1}-IDSDS}$ then:

(A2) $\models \mathsf {CBel}_{Agt} \mathsf {AllPRat}_{Agt}\rightarrow \neg pl(s)$

Let us take an arbitrary model M and world w and assume that $M,w \models \mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}$ and $M,w \models pl(s)$. We are going to show that $\mathit {s}_{} \in \mathit {S}_{m+1}^{\mathit {DWDS}^1-\mathit {IDSDS}}$.

From $M,w \models \mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}$, by the validity (10f) in Proposition 17, it follows that:

(B2) $M,w \models \mathsf {AllPRat}_{Agt}$

By the validity (9b) in Proposition 16, (B2) implies that:

(C2) $M,w \models \mathsf {AllSRat}_{Agt}$

Moreover we have the following validity by the property $\models \mathsf {CBel}_{Agt} \varphi \rightarrow \mathsf {Bel}_{i} \mathsf {CBel}_{Agt} \varphi$ for every i ∈ Agt:

(D2) $\models \mathsf {CBel}_{Agt} \mathsf {AllPRat}_{Agt}\rightarrow \bigwedge _{i \in Agt} \mathsf {Bel}_{i}\mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}$

Therefore, from $M,w \models \mathsf {CBel}_{Agt} \mathsf {AllPRat}_{Agt}$ we infer that:

(E2) $M,w \models \bigwedge _{i \in Agt} \mathsf {Bel}_{i}\mathsf {CBel}_{Agt}\mathsf {AllPRat}_{Agt}$

By the inductive hypothesis, Axiom K and the rule of necessitation for the belief operator Bel _i , from (E2) it follows that if $s^{\prime }\not \in S_{m}^{DWDS^{1}-IDSDS}$ then:

(F2) $M,w \models \bigwedge _{i\in Agt}\mathsf {Bel}_{i}\neg pl(s^{\prime })$

From (F2), (C2) and $M,w \models pl(s)$ it follows that for every i ∈ Agt and for all $b_{i}\in S_{i}$ either there is $s^{\prime }\in S_{m}^{DWDS^{1}-IDSDS}$ such that $\langle b_{i},s_{-i}^{\prime }\rangle <_{i}\langle s[i], s_{-i}^{\prime }\rangle$ or for all $\mathit {s}^{\prime }\in S_{m}^{DWDS^{1}-IDSDS}$ we have $\langle b_{i},s_{-i}^{\prime }\rangle \leq _{i}\langle s[i], s_{-i}^{\prime } \rangle$. The latter implies that for every i ∈ Agt we have $s[i] \in S_{i, m+1}^{DWDS^{1}-IDSDS}$ which is equivalent to $s\in S_{m+1}^{DWDS^{1}-IDSDS}$. □

1.3 A.3 Proof of Theorem 5

Let $s\not \in S^{DWDS^{2}-IDSDS}$. Then:

$$\models \mathsf{CBel}_{Agt}(\mathsf{AllPRat}_{Agt}\wedge \mathsf{AllRBelPRat}_{Agt}) \rightarrow \neg pl(s) $$

Proof

The proof is by induction. The proof of the inductive case goes exactly as the proof of the inductive case in the proof of Theorem 4.

Here we only prove the base case.

Base case  For all $s\not \in S_{2}^{DWDS^{2}-IDSDS}$ we prove that:

(A) $\models \mathsf {CBel}_{Agt}(\mathsf {AllPRat}_{Agt}\wedge \mathsf {AllRBelPRat}_{Agt})\rightarrow \neg pl(s)$

To prove (A), it is sufficient to prove the following validity (B), as $\mathsf {CBel}_{Agt}(\mathsf {AllPRat}_{Agt}\wedge \mathsf {AllRBelPRat}_{Agt}) \rightarrow (\mathsf {AllPRat}_{Agt}\wedge \mathsf {AllRBelPRat}_{Agt})$is valid.²⁰

For all $s\not \in S_{2}^{DWDS^{2}-IDSDS}$ we have that:

(B) $\models (\mathsf {AllPRat}_{Agt}\wedge \mathsf {AllRBelPRat}_{Agt})\rightarrow \neg pl(s)$

And to prove (B), it is sufficient to prove that if $s[i] \not \in S_{i,2}^{DWDS^{2}-IDSDS}$ then:

(C) $\models (\mathsf {PRat}_{i}\wedge \bigwedge _{\chi _{-i}\in Beh_{-i}:Comp(\chi _{-i},\mathsf {AllPRat}_{-i})}\mathsf {RBel}_{i}({\chi _{-i}},{\mathsf {AllPRat}_{-i}}))\rightarrow \neg pl_{i}(s[i])$

Let us prove (C) by reductio ad absurdum. We assume that $s[i] \not \in S_{i,2}^{DWDS^{2}-IDSDS}$ and $M,w \models \mathsf {PRat}_{i}$ and $M,w \models \bigwedge _{\chi _{-i}\in Beh_{-i}:Comp(\chi _{-i},{\mathsf {AllPRat}_{-i}})}\mathsf {RBel}_{i}({\chi _{-i}},{\mathsf {AllPRat}_{-i}})$ and $M,w \models pl_{i}(s[i])$ for some arbitrary PDL-A ⁺ model $M = \langle W, \{\mathcal {E}_{i}: i \in Agt\} , \kappa , \{\mathit {A}_{i} : i \in Agt\} , \mathit {V} \rangle$ and world w in M. We are going to show that these three facts are inconsistent.

The rest of the proof makes use of the following Lemma 1.

Lemma 1

Let $M = \langle W, \{\mathcal {E}_{i}: i \in Agt\}, \kappa , \{\mathcal {A}_{i}: i \in Agt\}, {\mathit {V}} \rangle$ be a PDL-A ⁺ model. If $M,w \models \bigwedge _{\chi _{-i} \in Beh_{-i}: Comp(\chi _{-i},\mathsf {AllPRat}_{-i})} \mathsf {RBel}_{i}({\chi _{-i}},{\mathsf {AllPRat}_{-i}})$ and $s_{-i}\in S_{-i, 1}^{DWDS^{2}-IDSDS}$ and $s_{-i}^{\prime }\not \in S_{-i,1}^{DWDS^{2}-IDSDS}$ then $\kappa _{w,i} (pl_{-i}(s_{-i}))< \kappa _{w,i} (pl_{-i}(s_{-i}^{\prime }))$. □

Proof

In order to prove Lemma 1, we first prove the following Lemma 2.

Lemma 2

Let $\chi _{-i} = \bigvee _{s_{-i}\in \mathbf {s}_{-i}}pl_{-i}(s_{-i})$ for some $\mathbf {s}_{-i}\subseteq S_{-i}$. Then, $Comp(\chi _{-i},\mathsf {AllPRat}_{-i})$ if and only if there exists $s_{-i}\in \mathbf {s}_{-i}$ such that $s_{-i} \in S_{-i, 1}^{DWDS^{2}-IDSDS}$. □

Proof

($\Leftarrow$) We first prove the right-to-left direction of the equivalence, after assuming that the set of strategy profiles is $S= \{s_{1},\ldots , s_{n}\}$ for some $n \in \mathbb {N}$. Suppose that $s_{-i}\in S_{-i,1}^{DWDS^{2}-IDSDS}$ with $s_{-i}\in \mathbf {s}_{-i}$. We can exhibit the following PDL-A ⁺ model $M^{\ast } = \langle W^{\ast },\{\mathcal {E}_{i}^{\ast } : i \in Agt\}, \kappa ^{\ast }, \{\mathit {A}_{i}^{\ast }: i\in Agt\}, {\mathit {V}}^{\ast } \rangle$ where:

• $W^{\ast } = \{w_{1}, \ldots , w_{n} \}$;

• for all i ∈ Agt, $\mathcal {E}_{i}^{\ast } = \{(w_{h}, w_{h^{\prime }}) : w_{h}, w_{h^{\prime }}\in W^{\ast }\;\text {and}\; s_{h} [i] =s_{h^{\prime }}[i]\}$;

• for all $w_{h} \in W^{\ast }$ and for all i ∈ Agt, $\mathcal {A}_{i}^{\ast } (w_h) = s_{h}[i]$;

• for all i ∈ Agt and for all $w_{h} \in W^{\ast }$, $\kappa ^{\ast }(w_{h},i)=0$;

• for all $w_{h} \in W^{\ast }$, ${\mathit {V}}^{\ast }(w_h) = Prop$.

It is straightforward to verify that $M^{\ast }, w^{\ast } \models pl_{-i} (s_{-i})\wedge \mathsf {AllPRat}_{-i}\wedge$ where $w^{\ast }$ is a world in $W^{\ast }$ such that $\mathcal {A}_{-i}^{\ast }(w^{\ast }) = s_{-i}$. Therefore, model $M^{\ast }$ satisfies $pl_{-i}(s_{-i}) \wedge \mathsf {AllPRat}_{-i}$. It follows that $M^{\ast }$ satisfies $\chi _{-i} \wedge \mathsf {AllPRat}_{-i}$ too.

(⇒) The left-to-right direction of the equivalence can be proved by reductio ad absurdum. We assume that: (1) $s_{-i}\not \in S_{-i, 1}^{DWDS^{2}-IDSDS}$ for all $s_{-i}\in \mathbf {s}_{-i}$ and (2) there exists $s_{-i}^{\prime } \in \mathbf {s}_{-i}$ such that $M,w \models pl_{-i}(s_{-i}^{\prime })\wedge \mathsf {AllPRat}_{-i}$ for some PDL-A ⁺ model M and world w in M. From the assumption (1), it follows that there is $j \in Agt\setminus \{i\}$ such that $s_{-i}^{\prime }[j] \not \in S_{j, 1}^{DWDS^{2}-IDSDS}$. From the definition of $\mathsf {PRat}_{j}$, by the Constraint (Constr3) over PDL-A ⁺ models, we can prove that if $s_{-i}^{\prime }[j] \not \in S_{j, 1}^{DWDS^{2}-IDSDS}$ and $M,w \models pl_{j}(s_{-i}^{\prime }[j])$then $M,w \models \neg \mathsf {PRat}_{j}$. Hence, from the initial assumptions it follows that $M,w \models \neg \mathsf {PRat}_{j}$. The latter is in contradiction with the assumption (2). □

Now assume that $s_{-i}\in S_{-i, 1}^{DWDS^{2}-IDSDS}$ and $s_{-i}^{\prime } \not \in S_{-i, 1}^{DWDS^{2}-IDSDS}$. By Lemma 2, it follows that $Comp(pl_{-i}(s_{-i})\vee pl_{-i}(s_{-i}^{\prime }),\mathsf {AllPRat}_{-i})$. Moreover, assume that $M,w \models \bigwedge _{\chi _{-i}\in Beh_{-i}:Comp(\chi _{-i},\mathsf {AllPRat}_{-i})} \mathsf {RBel}_{i}({\chi _{-i}},{\mathsf {AllPRat}_{-i}})$. From the latter assumption it follows that $M,w \models \mathsf {RBel}_{i}({pl_{-i}(s_{-i})\vee pl_{-i}(s_{-i}^{\prime })}{\mathsf {AllPRat}_{-i}})$. Hence $M, w \models [*_{i}^{\alpha } pl_{-i} (s_{-i})\vee pl_{-i}(s_{-i}^{\prime })]\mathit {Bel}_{i}\mathit {AIIPRat}_{-i}$ for any $\alpha \in Num \setminus \{ 0 \}$. By Lemma 2, from the assumption $s_{-i}^{\prime }\not \in S_{-i, 1}^{DWDS^{2}-IDSDS}$ it follows that $pl_{-i}(s_{-i}^{\prime })\wedge \neg \mathsf {AllPRat}_{-i}$ is valid. By the Constraint (Constr3) over PDL-A ⁺ models and the truth condition of the belief revision operator $[*_{i}^{\alpha } \varphi ]$, it follows that $M,w \models [*_{i}^{\alpha } pl_{-i}(s_{-i})\vee pl_{-i}(s_{-i}^{\prime })]\mathit {Bel}{i} (pl_{-i}(s_{-i})\wedge \neg pl_{-i}(s_{-i}^{\prime }))$. The latter implies $\kappa _{w,i} (pl_{-i}(s_{-i})) < \kappa _{w,i } (pl_{-i} (s_{-i}^{\prime }))$. This completes the proof of Lemma 1.

From $M,w \models \bigwedge _{\chi _{-i} \in Beh_{-i}:Comp(\chi _{-i}, \mathsf {AllPRat}_{-i})} \mathsf {RBel}_{i}({\chi _{-i}},{\mathsf {AllPRat}_{-i}})$, by Lemma 1, it follows that:

(D) if $\mathit {s}_{-i}^{\prime }\in S_{-i, 1}^{DWDS^{2}-IDSDS}$ and $s_{-i}^{\prime \prime }\not \in S_{-i, 1}^{DWDS^{2}-IDSDS}$ then $\kappa _{w,i} (pl_{-i} (s_{-i}^{\prime }))<\kappa _{w,i } (pl_{-i}(s_{-i}^{\prime \prime }))$.

$s[i]\not \in S_{i,2}^{DWDS^{2}-IDSDS}$ implies that:

(E1) $s[i] \not \in S_{i,1}^{DWDS^{2}-IDSDS}$ or

(E2) $s[i]\in S_{i,1}^{DWDS^{2}-IDSDS}$ and $s[i] \not \in S_{i,2}^{DWDS^{2}-IDSDS}$

We split the proof in the two subcases: (E1) and (E2).

Proof for the Case (E1)

$s[i] \not \in S_{i,1}^{DWDS^{2}-IDSDS}$ implies that:

(F1) there is $b_{i} \in S_{i}^{DWDS^{2}-IDSDS}$ such that: (1) $b_{i} \neq s[i]$ and (2) $\langle s[i],s_{-i}^{\prime }\rangle <_{i}\langle b_{i}, s_{-i}^{\prime }\rangle$ for some $s_{-i}^{\prime } \in S_{-i}^{DWDS^{2}-IDSDS}$ and (3) $\langle s[i],s_{-i}^{\prime \prime }\rangle \leq _{i}\langle b_{i},s_{-i}^{\prime \prime }\rangle$ for all $s_{-i}^{\prime \prime }\in S_{-i}^{DWDS^{2}-IDSDS}$.

From (F1) by the Constraint (Constr3) it follows that:

(G1) there are $b_{i} \in S_{i}^{DWDS^{2}-IDSDS}$ and $s_{-i}^{\prime }\in S_{-i}^{DWDS^{2}-IDSDS}$ and $v \in W$ such that: (1) $\mathit {b}_{i}\neq s[i]$ and (2) $(w,v) \in \mathcal {E}_{i}$ and (3) $M,v \models pl_{-i}(s_{-i}^{\prime })$ and (4) $\langle s[i],s_{-i}^{\prime }\rangle <_{i}\langle b_{i},s_{-i}^{\prime }\rangle$ and (5) for all $u \in W$ such that $(w,u) \in \mathcal {E}_{i}$ and for all $s_{-i}^{\prime \prime }\in S_{-i}^{DWDS^{2}-IDSDS}$: if $M, u \models pl_{-i} (s_{-i}^{\prime \prime })$ then $\langle s[i],s_{-i}^{\prime \prime }\rangle \leq _{i} \langle b_{i},s_{-i}^{\prime \prime }\rangle$.

But (G1) is in contradiction with $M, w \models \mathsf {PRat}_{i}$ and $M,w \models pl_{i} (s[i])$.

Proof for the case (E2)

(E2) implies that:

(F2) there is $b_{i} \in S_{i,1}^{DWDS^{2}-IDSDS}$ such that: (1) $b_{i} \neq s[i]$ and (2) $\langle s[i],s_{-i}^{\prime }\rangle <_{i}\langle b_{i},s_{-i}^{\prime }\rangle$ for some $s_{-i}^{\prime }\in S_{-i,1}^{DWDS^{2}-IDSDS}$ and (3) $\langle s[i],s_{-i}^{\prime }\rangle \leq _{i} \langle b_{i},s_{-i}^{\prime \prime }\rangle$ for all $s_{-i}^{\prime \prime }\in S_{-i,1}^{DWDS^{2}-IDSDS}$.

By the Constraint (Constr3), (F2) together with $M, w \models \mathsf {PRat}_{i}$ and $M,w \models pl_{i}(s[i])$ imply that:

(G2) there are $s_{-i}^{\prime }\in S_{-i,1}^{DWDS^{2}-IDSDS}$ and $s_{-i}^{\prime \prime }\not \in S_{-i,1}^{DWDS^{2}-IDSDS}$ such that $\kappa _{w,i} (pl_{-i} (s_{-i}^{\prime })) \leq \kappa _{w,i } (pl_{-i}(s_{-i}^{\prime \prime }))$.

But (G2) is in contradiction with (D).

1.4 A.4 Proof of Theorem 6

Let $\mathit {s}_{} \not \in \mathit {S}_{}^{\mathit {DWDS}^{k+1}-\mathit {IDSDS}}$ and k > 0. Then:

$$\models \mathsf{CBel}_{Agt} \mathsf{AllPRatRBelPRat}_{\mathit{Agt}, k} \rightarrow \neg \mathit{pl}_{} (\mathit{s}_{} ) $$

Proof

The proof is by induction. The proof of the inductive case goes exactly as the proof of the inductive case in the proof of Theorem 4.

Here we only prove the base case.

Base case  For all $\mathit {s}_{} \not \in \mathit {S}_{k+1}^{\mathit {DWDS}^{k+1}-\mathit {IDSDS}}$ we prove that:

(A1) $\models \mathsf {CBel}_{Agt} \mathsf { AllPRatRBelPRat}_{\mathit {Agt}, k} \rightarrow \neg \mathit {pl}_{} (\mathit {s}_{} )$

To prove (A1), it is sufficient to prove the following validity (B1), as $\mathsf {CBel}_{Agt} \mathsf { AllPRatRBelPRat}_{\mathit {Agt}, k} \rightarrow \mathsf { AllPRatRBelPRat}_{\mathit {Agt}, k}$ is valid (the proof of this validity is similar to the one given in the proof of Theorem 5 for the validity $\mathsf {CBel}_{Agt} \mathsf {AllPRat}_{ \mathit {Agt} } \rightarrow \mathsf {AllPRat}_{ \mathit {Agt} }$).

For all $\mathit {s}_{} \not \in \mathit {S}_{k+1}^{\mathit {DWDS}^{k+1}-\mathit {IDSDS}}$ we have that:

(B1) $\models \mathsf {AllPRatRBelPRat}_{\mathit {Agt}, k} \rightarrow \neg \mathit {pl}_{}(\mathit {s}_{} )$

We prove something more general than (B1), namely we prove that for all $J \in 2^{\mathit {Agt}*}$ and for all $\mathit {s}_{J } \not \in \mathit {S}_{J, k+1}^{\mathit {DWDS}^{k+1}-\mathit {IDSDS}}$:

(C1) $\models \mathsf { AllPRatRBelPRat}_{J, k} \rightarrow \neg \mathit {pl}_{J } (\mathit {s}_{J} )$

The proof of (C1) is again by induction.

Base case  For all $\mathit {s}_{J } \not \in \mathit {S}_{J, 2}^{\mathit {DWDS}^{2}-\mathit {IDSDS}}$ we have to prove that:

(A2) $\models ( \mathsf {AllPRat}_{ J } \wedge \mathsf { AllRBelPRat}_{J } ) \rightarrow \neg \mathit {pl}_{J } (\mathit {s}_{J } )$

In the proof of Theorem 5 we have proved something stronger than (A2), namely we have proved that if $\mathit {s}_{} [i] \not \in \mathit {S}_{i,2}^{\mathit {DWDS}^2-\mathit {IDSDS}}$ then $\models (\mathsf {PRat}_{i}\wedge \bigwedge _{\chi _{-i}\in \mathit {Beh}_{-i}:\mathit {Comp} (\chi _{-i }{,} \mathsf {AllPRat}_{-i})}\mathsf {RBel}_{i}({\chi _{-i}},{\mathsf {AllPRat}_{-i}}))\rightarrow \neg \mathit {pl}_{i}(\mathit {s}_{} [i])$.

Inductive case  Let m be an integer such that m > 1. Let us assume that for all $J \in 2^{\mathit {Agt}*}$, if $\mathit {s}_{J } \not \in \mathit {S}_{J, m}^{\mathit {DWDS}^{m}-\mathit {IDSDS}}$ then:

• (Inductive Hypothesis)  $\models \mathsf { AllPRatRBelPRat}_{J, m-1} \rightarrow \neg \mathit {pl}_{J } (\mathit {s}_{J } )$

We are going to prove that if $\mathit {s}_{J } \not \in \mathit {S}_{J, m+1}^{\mathit {DWDS}^{m+1}-\mathit {IDSDS}}$ then:

• (A3) $\models \mathsf { AllPRatRBelPRat}_{J, m} \rightarrow \neg \mathit {pl}_{J } (\mathit {s}_{J } )$

  The proof is by reduction ad absurdum. We take an arbitrary PDL-A ⁺ model M and a world w in M. We assume that $M,w \models \mathsf {AllPRatRBelPRat}_{J, m}$ and $M,w \models \mathit {pl}_{J } (\mathit {s}_{J})$ and $\mathit {s}_{J} \not \in \mathit {S}_{J, m+1}^{\mathit {DWDS}^{m+1}-\mathit {IDSDS}}$. We are going to show that these three facts are inconsistent.

  The rest of the proof is based on the following Lemma 3. □

Lemma 3

Let m be an integer such that m > 1 and let $\chi _{-i}=\bigvee _{\mathit {s}_{-i} \in \mathbf {s}_{-i}}\mathit {pl}_{-i}(\mathit {s}_{-i})$ for some $\mathbf {s}_{-i}\subseteq \mathit {S}_{-i}$. Then, $\mathit {Comp} (\chi _{-i}{,}\mathsf {AllPRatRBelPRat}_{-i,m-1})$ if and only if there exists $\mathit {s}_{-i}\in \mathbf {s}_{-i}$ such that $\mathit {s}_{-i } \in \mathit {S}_{-i, m}^{\mathit {DWDS}^{m}-\mathit {IDSDS}}$.

Proof of Sketch

The proof of Lemma 3 is again by induction. We only prove the base case (i.e., when $m =2$).

($\Leftarrow$) We first prove the right-to-left direction of the equivalence, after assuming that the set of strategy profiles is $\mathit {S}_{} = \{\mathit {s}_{1}, \ldots , \mathit {s}_{n}\}$ for some $n \in \mathbb {N}$. Suppose that $\mathit {s}_{-i } \in \mathit {S}_{-i, 2}^{\mathit {DWDS}^2-\mathit {IDSDS}}$ with $\mathit {s}_{-i } \in \mathbf {s}_{-i}$. We can exhibit the following PDL-A ⁺ model $M^{\ast } = \langle W^{\ast }, \{\mathcal {E}_{i }^{\ast }: i \in \mathit {Agt}\} , \kappa ^{\ast }, \{\boldsymbol {\mathit {A}}_{i}^{\ast } : i \in \mathit {Agt} \}, {\mathit {V}}^{\ast }\rangle$ where:

• $W^{*} = \{w_{1}, \ldots , w_{n} \}$;

• for all i ∈ Agt, $\mathcal {E}_{i }^{*} = \{(w_{h}, w_{h{\prime }}) : w_{h}, w_{h{\prime }}\in W^{*} \;\text {and}\; \mathit {s}_{h} [i] = \mathit {s}_{h{\prime }}[i]\}$;

• for all $w_{h} \in W^{*}$ and for all i ∈ Agt, $\mathcal {A}_{i }^{*} (w_h) = \mathit {s}_{h } [i]$;

• for all i ∈ Agt and for all $w_{h} \in W^{*}$:

  • 1. $\kappa ^{*}(w_{h}, i)=0$ if and only if, for all j ∈ Agt∖{i}, $\mathit {s}_{h}[j] \in \mathit {S}_{j, 1 }^{\mathit {DWDS}^{2}-\mathit {IDSDS}}$,

  • 2. $\kappa ^{*}(w_{h},i)= \mathsf {max}$ if and only if there is $j \in \mathit {Agt} \setminus \{i\}$ such that $\mathit {s}_{h} [j] \not \in \mathit {S}_{j,1 }^{\mathit {DWDS}^{2}-\mathit {IDSDS}}$;

• for all $w_{h} \in W^{*}$, ${\mathit {V}}^{*}(w_h) = \mathit {Prop}$.

With the help of Lemma 2 in Section A.3, it is straightforward to verify that $M^{*}, w^{*} \models \mathit {pl}_{-i}(\mathit {s}_{-i})\wedge \mathsf {AllPRat}_{-i}$ $\bigwedge _{j \in \mathit {Agt} \setminus \{i\}}\left (\bigwedge _{\substack {\chi _{-j}\in Beh_{-j}:\\ \mathit {Comp} (\chi _{-j}{,} \mathsf {AllPRat}_{-j})}}\right .$ $\left .\mathsf {RBel}_{j}({\chi _{-j}},{ \mathsf {AllPRat}_{-j}})\right )$ where $w^{*}$ is a world in $W^{*}$ such that $\mathcal {A}_{-i}^{*} (w^{*} ) = \mathit {s}_{-i }$. Therefore, model $M^{*}$ satisfies $\mathit {pl}_{-i} (\mathit {s}_{-i }) \wedge \mathsf {AllPRatRBelPRat}_{-i, 1}$. It follows that $M^{*}$ satisfies $\chi _{-i} \wedge \mathsf {AllPRatRBelPRat}_{-i, 1}$ too.

(⇒) The left-to-right direction of the equivalence can be proved by reductio ad absurdum. We assume that: (1) $\mathit {s}_{-i } \not \in \mathit {S}_{-i, 2}^{\mathit {DWDS}^2-\mathit {IDSDS}}$ for all $\mathit {s}_{-i } \in \mathbf {s}_{-i}$ and (2) there exists $\mathit {s}_{-i}^{\prime } \in \mathbf {s}_{-i}$ such that $M, w \models \mathit {pl}_{-i}(\mathit {s}_{-i}^{\prime })\wedge \mathsf {AllPRat}_{-i}\wedge$ $\bigwedge _{j \in \mathit {Agt}\setminus \{i\}}(\bigwedge _{\substack {\chi _{-j} \in Beh_{-j}: \\ \mathit {Comp}(\chi _{-j}{,}\mathsf {AllPRat}_{-j})}} \mathsf {RBel}_{j}({\chi _{-j}},{\mathsf {AllPRat}_{-j}}))$ for some PDL-A ⁺ model M and world w in M. From the assumption (1), it follows that there is $j \in \mathit {Agt} \setminus \{ i \}$ such that $\mathit {s}_{- i } '[j] \not \in \mathit {S}_{j, 2}^{\mathit {DWDS}^2-\mathit {IDSDS}}$. From the definition of $\mathsf {PRat}_{j} ( \mathit {s}_{- i } '[j] )$, by the Constraint (Constr3) over PDL-A ⁺ models and with the help of Lemma 1 in Section A.3, we can prove that if $\mathit {s}_{-i} '[j] \not \in \mathit {S}_{j, 2}^{\mathit {DWDS}^2-\mathit {IDSDS}}$ and $M,w \models \bigwedge _{\substack {\chi _{-j}\in Beh_{-j}: \\ {\mathit {Comp}(\chi _{-j }{,} \mathsf {AllPRat}_{-j})}}} \mathsf {RBel}_{j}({\chi _{-j}},{\mathsf {AllPRat}_{-j}})$then $M,w \models \neg \mathsf {PRat}_{j} ( \mathit {s}_{- i } '[j] )$. Therefore, from the initial assumption that $M,w \models \mathit {pl}_{-i } ( \mathit {s}_{-i } ' )$ it follows that $M,w \models \neg \mathsf {PRat}_{ j }$. The latter is in contradiction with the assumption (2), namely with $M,w \models \mathsf {AllPRat}_{-i }$.

$M,w \models \mathsf { AllPRatRBelPRat}_{J, m}$ is equivalent to:

(B3) $M,w \models \mathsf {AllPRat}_{J}\wedge \bigwedge _{i \in J}\bigwedge _{\chi _{-i}\in \mathit {Beh}_{-i}:\mathit {Comp}}$

$\times (\chi _{-i} {,} \mathsf { AllPRatRBelPRat}_{-i, m-1}) \mathsf {RBel}_{i}({\chi _{-i}},{\mathsf { AllPRatRBelPRat}_{-i, m-1}})$

By inductive hypothesis, (B3) implies that for all $\mathit {s}_{-i } '' \not \in \mathit {S}_{-i, m}^{\mathit {DWDS}^{m}-\mathit {IDSDS}}$:

(C3) $M,w \models \bigwedge _{i\in J} \bigwedge _{\chi _{-i} \in \mathit {Beh}_{-i}:\mathit {Comp}}$

$\times (\chi _{-i} {,} \mathsf {AllPRatRBelPRat}_{-i, m-1}) \mathsf {RBel}_{i}({\chi _{-i}}{\neg \mathit {pl}_{-i} (\mathit {s}_{-i}'')})$

From (C3) and Lemma 3 it follows that for all i ∈ J:

(D3) if $\mathit {s}_{-i}{\prime }\in \mathit {S}_{-i, m}^{\mathit {DWDS}^m-\mathit {IDSDS}}$ and $\mathit {s}_{-i}{\prime }{\prime }\not \in \mathit {S}_{-i, m}^{\mathit {DWDS}^m-\mathit {IDSDS}}$ then $\kappa _{w, i} (\mathit {pl}_{-i}(\mathit {s}_{-i}{\prime })) < \kappa _{w, i }(\mathit {pl}_{-i }(\mathit {s}_{-i}{\prime }{\prime }))$.

(The proof of the preceding item (D3) is similar to the proof of the item (D) in the proof of Theorem 5 in Section A.3).

The rest of the proof proceeds as the proof of Theorem 5 in Section A.3 (starting from item (D)). For this reason, we do not repeat it here. □