Reduction of Nonautonomous Population Dynamics Models with Two Time Scales

Abstract

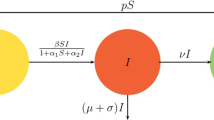
The purpose of this work is reviewing some reduction results to deal with systems of nonautonomous ordinary differential equations with two time scales. They could be included among the so-called approximate aggregation methods. The existence of different time scales in a system, together with some long-term features, are used to build up a simpler system governed by a lesser number of state variables. The asymptotic behavior of the latter system is then used to describe the asymptotic behaviour of the former one. The reduction results are stated in two particular but important cases: periodic systems and asymptotically autonomous systems. The reduction results are illustrated with the help of simple spatial SIS epidemic models including either periodic or asymptotically autonomous terms.

Appendix

We summarize in the next theorem the results on singular perturbations methods for slow-fast dynamics on the infinite interval as presented for the first time in the work of Hoppensteadt (1966), that the author subsequently included in a more readable way in reviews of differential equations with small parameters and quasi-static state analysis of differential equations (Hoppensteadt 1971, 1993, 2010). In Verhulst (2007) it is found a review of singular perturbation methods for slow-fast systems where they are mentioned some other works, notably by Tikhonov et al. (1985), that preceded those of Hoppensteadt though for bounded intervals of time. It is also found in Verhulst (2007) the peculiarities of this theory applied to autonomous equations following the works by Fenichel (1971).

Theorem 6

Let us consider the initial-value problem

$$\begin{aligned} \left\{ \begin{array}{rl} \varepsilon \dfrac{dx}{dt}=f(t,x,y,\varepsilon ), &{} x(t_0)=x_0, \\ \dfrac{dy}{dt}=g(t,x,y,\varepsilon ), &{} y(t_0)=y_0, \end{array}\right. \end{aligned}$$

(24)

where $x\in \mathbb {R}^n$, $y\in \mathbb {R}^m$ and $\varepsilon$ is a small positive parameter. We call $\hat{\Omega }=\Omega \times [0,\varepsilon _0]$ where $\Omega =I\times B_R\times B_{R'}$, $I=[t_0, \infty \}$, $B_R=\{x\in \mathbb {R}^n:|x|\le R\}$, $B_{R'}=\{y\in \mathbb {R}^m:|y|\le R'\}$ and $\varepsilon _0$ is a positive constant. Balls $B_{R}$ and $B_{R'}$ could be replaced by any sets that are diffeomorphic to them.

• Hypothesis H1. $f,\,g\in \mathcal {C}^2(\hat{\Omega })$ and the solutions of the system (24) beginning in $B_R\times B_{R'}$ remains there for $t\in I$.

• Hypothesis H2. There is a function $x=\varPhi (t,y)\in \mathcal {C}^2$ such that $f(t,\varPhi (t,y),y,0)=0$ for $(t,y)\in I\times B_{R'}$.

• Hypothesis H3. $x=\varPhi (t,y)$ is an asymptotically stable equilibrium of the system $\dfrac{dx}{d\tau }=f(t,x,y,0)$ uniformly in $(t,y)\in I\times B_{R'}$ and $x_0$ is in the domain of attraction of $\varPhi (t_0,y_0)$.

• Hypothesis H4. The system of equations $d\bar{y}/dt=g(t,\varPhi (t,\bar{y}),\bar{y},0)$ has an uniformly asymptotically stable solution $y^*(t)$ for $t_0\le t< \infty$ and $y_0$ is in its domain of attraction.

Then if $\bar{y}(t)$ is the solution of

$$\begin{aligned} \begin{array}{rl} d\bar{y}/dt=g(t,\varPhi (t,\bar{y}),\bar{y},0),&\bar{y}(t_0)=y_0, \end{array} \end{aligned}$$

for sufficiently small values of $\varepsilon$ the solution $(x(t),y(t))$ of the system (24) satisfies

$$\begin{aligned} x(t)=\varPhi (t,\bar{y}(t))+o(1), \qquad y(t)=\bar{y}(t)+o(1), \end{aligned}$$

as $\varepsilon \rightarrow 0^+$ uniformly on any interval of the form $t_0<t_1\le t < \infty$.