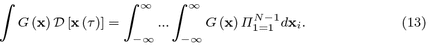Skip to main content
SpringerLink
Log in

The Principle of Minimal Resistance in Non-equilibrium Thermodynamics

  • Published:
Foundations of Physics Aims and scope Submit manuscript

Abstract

Analytical models describing the motion of colloidal particles in given force fields are presented. In addition to local approaches, leading to well known master equations such as the Langevin and the Fokker–Planck equations, a global description based on path integration is reviewed. A new result is presented, showing that under very broad conditions, during its evolution a dissipative system tends to minimize its energy dissipation in such a way to keep constant the Hamiltonian time rate, equal to the difference between the flux-based and the force-based Rayleigh dissipation functions. In fact, the Fokker–Planck equation can be interpreted as the Hamilton–Jacobi equation resulting from such minumum principle. At steady state, the Hamiltonian time rate is maximized, leading to a minimum resistance principle. In the unsteady case, we consider the relaxation to equilibrium of harmonic oscillators and the motion of a Brownian particle in shear flow, obtaining results that coincide with the solution of the Fokker–Planck and the Langevin equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Clearly, this is true only when the system is close to its equilibrium configuration, since, in general, phenomenological coefficients are far from being constant; for example, in the case of heat conduction, thermal conductivity, relating heat current and temperature gradient, should vary with temperature as \(T^{-2}\), which is very unlikely, and so the principle of minimum entropy production should be taken with great caution.

  2. Denoting \( \epsilon = t / N \), \( t_i = i \epsilon \) and \( \mathbf x _i = \mathbf x (t_i) \), the path integral is defined as the following functional integral:

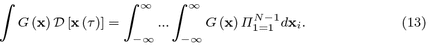
    A rigorous and complete treatment on functional integration applied on diffusion processes can be found in Graham [26].

  3. This can also be proved explicitly, multiplying Eq. (23) by \(\dot{\mathbf{y}}\) and considering that \( \frac{d}{dt} = \frac{\partial }{\partial t} + \dot{\mathbf{y}} \cdot \mathbf{\nabla }\), obtaining \( d\mathcal H /dt = 0 \), i.e. \(\mathcal H \) is constant, along the minimum path.

References

  1. Kirchhoff, G.D.: Ueber die Anwendbarkeit der Formeln for die Intensitfiten der galvanischen Strome in einem Systeme linearer leiter auf Systemen, die zum Theil aus nicht linearem Leitern bestehen. Ann. Phys. 75, 189–205 (1848)

    Article  Google Scholar 

  2. Prigogine, I.: Introduction to Thermodynamics of Irreversible Processes, 2nd edn. Interscience, New York (1961)

    MATH  Google Scholar 

  3. De Groot, S.R., Mazur, P.: Non-Equilibrium Thermodynamics. North Holland, Amsterdam (1962)

    Google Scholar 

  4. Jaynes, E.T.: The minimum entropy production principle. Ann. Rev. Phys. Chem. 31, 579–601 (1980)

    Article  ADS  Google Scholar 

  5. Müller, I., Weiss, W.: Thermodynamics of irreversible processes - past and present. Eur. Phys. J. H 37, 139–236 (2012)

    Article  Google Scholar 

  6. Ziegler, H.: An Introduction to Thermomechanics. North-Holland, Amsterdam (1983)

    MATH  Google Scholar 

  7. Hill, R.: The Mathematical Theory of Plasticity. Oxford University Press, Oxford (1950)

    MATH  Google Scholar 

  8. Onsager, L.: Reciprocal relations in irreversible processes II. Phys. Rev. 38, 2265–2279 (1931)

    Article  ADS  MATH  Google Scholar 

  9. Onsager, L., Machlup, S.: Fluctuations and irreversible processes. Phys. Rev. 91, 1505–1512 (1953)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Gyarmati, I.: Non-Equilibrium Thermodynamics. Springer, Heidelberg (1970)

    Book  Google Scholar 

  11. Zupanović, P., Yuretić, D., Botrić, S.: Kirchhoff’s loop law and the maximum entropy production principle. Phys. Rev. E 70, 056108 (2004)

    Article  ADS  Google Scholar 

  12. Martyushev, L.M., Seleznev, V.D.: Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 426, 1–45 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  13. Dewar, R.C.: Maximum entropy production and the fluctuation theorem. J. Phys. A 38, L371–L381 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Favretti, M.: The maximum entropy rate description of a thermodynamic system in a stationary non-equilibrium state. Entropy 11, 675–687 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Polettini, M.: Fact-checking Ziegler’s maximum entropy production principle beyond the linear regime and towards steady state. Entropy 15, 2570–2584 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  16. Martyushev, L.M.: Entropy and entropy production: old misconceptions and new breakthroughs. Entropy 15, 1152–1170 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Verhàs, J.: Gyarmati’s variational principle of dissipative processes. Entropy 16, 2362–2383 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  18. Salamon, P., Hoffmann, K.H., Schubert, S., Berry, R.S., Andresen, B.: What conditions make minimum entropy production equivalent to maximum power production? J. Non Equilib. Thermodyn. 26, 73–83 (2001)

    Article  ADS  MATH  Google Scholar 

  19. Polettini, M.: Macroscopic constraints for the minimum entropy production principle. Phys. Rev. E 84(051117), 1–9 (2011)

    Google Scholar 

  20. Beretta, G.P.: Modeling non-equilibrium dynamics of a discrete probability distribution: general rate equation for maximal entropy generation in a maximum-entropy landscape with time-dependent constraints. Entropy 10, 160–182 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Beretta, G.P.: Steepest entropy ascent model for far-nonequilibrium thermodynamics: unified implementation of the maximum entropy production principle. Phys. Rev. E 90, 1–14 (2014)

    Article  Google Scholar 

  22. Uhlenbeck, G.E., Ornstein, L.S.: On the theory of the Brownian motion. Phys. Rev. 36, 823–841 (1930)

    Article  ADS  MATH  Google Scholar 

  23. Mauri, R.: Non-Equilibrium Thermodynamics in Multiphase Flows. Springer, Heidelberg (2013)

    Book  MATH  Google Scholar 

  24. Mauri, R., Leporini, D.: Violation of the fluctuation-dissipation theorem in confined driven colloids. Europhys. Lett. 76, 1022–1028 (2006)

    Article  ADS  Google Scholar 

  25. Feynman, R.P., Hibbs, A.R.: Quantum Mechanics and Path Integrals. McGraw Hill, New York (1965)

    MATH  Google Scholar 

  26. Graham, R.: Path integral formulation of general diffusion processes. Z. Physik B 26, 281–290 (1977)

    Article  ADS  Google Scholar 

  27. Wang, Q.A., El Kaabouchiu, A.: From random motion of Hamiltonian systems to Boltzmann’s H theorem and second law of thermodynamics: a pathway by path probability. Entropy 16, 885–894 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  28. Gelfand, I.M., Yaglom, A.M.: Integration in function spaces and its application in quantum physics. J. Math. Phys. 1, 48–69 (1960)

    Article  ADS  Google Scholar 

  29. Schulman, L.S.: Techniques and Applications of Path Integration, Chapter 9. Interscience, New York (1981)

    Google Scholar 

  30. Wiener, N.: The average of an analytic functional. Proc Nat. Acad. Sci. USA 7, 253–260; 294–298 (1921)

  31. Wieger, F.W.: Introduction to Path Integral Methods in Physics and Polymer Science. World Scientific, Singapore (1986)

    Google Scholar 

  32. Martiouchev, L.M., Seleznev, V.D.: Maximum-entropy production principle as a criterion for the morphological-phase selection in the crystallization process. Dokl Phys 45, 129–131 (2000)

    Article  ADS  Google Scholar 

  33. Molin, D., Mauri, R.: Spinodal decomposition of binary mixtures with composition-dependent heat conductivities. Chem. Eng. Sci. 63, 2402–2407 (2008)

    Article  Google Scholar 

  34. Mauri, R., Haber, S.: Applications of the Wiener path integral for the diffusion of Brownian particles in shear flows. SIAM J. Appl. Math. 46, 49–55 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  35. Foister, R.T., Van De Ven, T.G.M.: Diffusion of Brownian particles in shear flows. J. Fluid Mech. 96, 105–132 (1980)

    Article  ADS  MATH  Google Scholar 

  36. Katayama, Y., Terauti, R.: Brownian motion of a single particle under shear flow. Eur. J. Phys. 17, 136–140 (1996)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Industrial Engineering, Laboratory of Reactive Multiphase Flows, Università di Pisa, 56126, Pisa, Italy

    Roberto Mauri

Authors
  1. Roberto Mauri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Roberto Mauri.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mauri, R. The Principle of Minimal Resistance in Non-equilibrium Thermodynamics. Found Phys 46, 393–408 (2016). https://doi.org/10.1007/s10701-015-9969-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10701-015-9969-3

Keywords

Search

Navigation