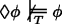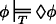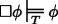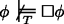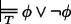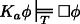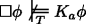Abstract
Epistemic contradictions are now a well-known and often discussed phenomenon among those who study epistemic modals. These contradictions are expressed by sentences like ‘It is raining and it might not be raining’ whose oddness to the common ear demands an explanation. However, it has turned out to be a rather controversial enterprise to provide such an explanation in a sufficiently precise and general manner. According to pragmatic explanations, epistemic contradictions are semantically consistent but pragmatically defective. According to semantic explanations, one should regard epistemic contradictions as plain semantic inconsistencies. Endorsing such a semantic solution is, however, tantamount to rejecting classical logic, which predicts the consistency of epistemic contradictions. After arguing that all existing solutions to this problem face as yet unmet challenges, I will present a new solution that adequately overcomes these challenges. I will propose to view epistemic contradictions as semantically consistent but epistemically defective sentences. The main thesis emerging will be that we need neither abandon the inference rules of classical logic nor the classical truth-conditional approach to semantics to deal adequately with epistemic contradictions.
Similar content being viewed by others
1 Introduction
Suppose someone utters one of these sentences to you:
-
1.#
It is raining and I don’t know that it is raining.
-
2.#
It is raining and it might not be raining.
You will be puzzled. Both of them sound blatantly weird. Why? A lively discussion over the last years shows that providing an adequate answer to that question is not a simple task. According to classical modal semantics developed in the last century, both sentences are perfectly consistent. For example, can’t it be raining without your knowing it? It does seem so. And isn’t 2 essentially communicating the same thing as 1? So what is going on here? We may—following Yalcin (2007)—refer to this problem as the problem of epistemic contradiction.
The literature offers two types of answers to this problem: (i) 2 is semantically inconsistent, (ii) 2 is pragmatically infelicitous but semantically consistent. Both solutions agree that 1 is only pragmatically infelicitous. The problem with i is that it threatens to validate the implausible inference from ‘It might not be raining’ to ‘It is not raining’. It is unclear which principles of classical logic we need to weaken in order to avoid this result. The problem with ii is that it cannot explain the different behaviour of 1 and 2 in certain contexts. While we may embed 1 felicitously (as in ‘If it is raining and I don’t know that it is raining, then I will not be prepared’), we cannot do so with 2 (as in ‘If it is raining and it might not be raining, then I will not be prepared’).
I shall offer a third kind of solution which is nonetheless pragmatic in spirit: sentences like 2 are epistemically defective but semantically consistent (and 1 is pragmatically infelicitous). The special kind of epistemic defectiveness of 2 can be traced back to the fact that 2 cannot even be assumed coherently. I shall argue that we may use this feature to construct an orthodox formal theory which delivers the desired results. If my solution succeeds, then it follows that epistemic contradictions are less troublesome than widely thought: there would be no need to develop a non-classical semantics in order to explain what is wrong with epistemic contradictions. In the next section, I will reconstruct the problem precisely. Then I shall briefly survey the existing solutions before turning to my theory in Section 4. After an informal exposition of the key ideas, I will make my solution formally precise. I end by discussing some potential worries about my solution.
2 Making the Problem Precise
As usual, I use ‘♢’ for the epistemic possibility operator (‘might’, ‘possibly’,...) and ‘\(\Box \)’ for the epistemic necessity operator (‘must’, ‘necessarily’,...). Throughout the paper, ‘p’ will denote an atomic sentence (like ‘It is raining’ or ‘It is sunny’) and the Greek letter ‘ϕ’ (and sometimes ‘ψ’) will denote sentences of arbitrary complexity. ‘⊥’ always denotes the absurd sentence. ‘K.’ will be the operator for knowledge, which has an argument place for the knower. Given this terminology, we can formalize the structure of the two variants of epistemic contradiction mentioned above:
-
(ECK)
p ∧¬Kap
-
(ECM)
p ∧♢¬p
In order to construct the problem precisely, we need another bit of terminology. First, let ‘Γ’ and ‘Δ’ denote arbitrary and possibly empty sets of sentences. Then let ‘\(\vDash \)’ denote the (correct) relation of logical consequence. I cannot say more about this consequence relation for now because what the meaning of ‘\(\vDash \)’ is will be part of the problem. ‘\({\varGamma } , \phi \vDash \psi \)’ is meant to be an abbreviation for ‘\({\varGamma } \cup \{\phi \} \vDash \psi \)’ and refers to the claim that ψ logically follows from all the sentences in Γ ∪{ϕ}. Finally, we need some logical ingredients:
-
(CON)
\(\phi ,\psi \vDash \phi \wedge \psi \)
Given these classical principles, our problem appears if we consider the following desideratum:
-
(DES)
\(p \wedge \Diamond \neg p \vDash \bot \)
According to (DES), (ECM) logically entails absurdity. This is the obvious way of saying that the modal variant of our epistemic contradictions is semantically inconsistent. However, a serious problem appears if we combine all these principles. We may derive an unacceptable result:

The result is that possibility sentences like ‘It might not be raining’ do logically entail their prejacent (‘It is not raining’). But this is wrong, as all authors writing on the topic like e.g DeRose (1991) or Yalcin (2007) point out. Our task now is to decide what is wrong here. The semantic solution accepts (DES) but needs to reject at least one of our additional logical principles. The orthodox pragmatic solution rejects (DES) and tries to explain the weirdness of (ECM) by appealing to pragmatic principles instead. In agreement with orthodoxy, I shall claim that we should reject (DES). But before we turn to my solution, let us consider the existing pragmatic and the semantic solutions.
3 Surveying the Options
3.1 The Pragmatic Solution
The traditional option is to keep the logic classical—i.e. to reject (DES)—and argue for a pragmatic explanation of the oddness of (ECM)—and (ECK). Representatives of this pragmatism like DeRose (1991), who bases his solution on Unger (1975), argue that the contradictory status of (ECM)—and (ECK)—comes to light if and only if an instance of it is asserted. The reasoning runs like this: Asserting a conjunction means asserting each conjunct. Thus, asserting (ECM) means asserting p and asserting ♢¬p. Asserting a sentence also conveys that the speaker knows that it is true. Thus, asserting p conveys that the speaker knows that p is true (Ksp). However, ♢¬p and Ksp are semantically inconsistent.Footnote 1 Thus, whenever a speaker asserts (ECM) there is an inconsistency between something the speaker says (♢¬p) and something the speaker pragmatically conveys (Ksp). The explanation for (ECK) is analogous. If we presuppose that the constant in the index refers to the speaker as in ‘It is raining and I don’t know it’ asserting it will also yield the result that the speaker says something (¬Ksp) which contradicts something she conveys (Ksp).
Everyone admits that the pragmatic solution perfectly works if we want to explain the oddness of (ECK). This oddness appears only if the referent of a is the speaker of the utterance. While it is odd to say 1, it is perfectly fine to utter ‘It is raining and she doesn’t know that it is raining’. Since the pragmatic solution for (ECK) only works if the referent is the speaker, it perfectly explains the case. However, some recent theorists, in particular Yalcin (2007) and Mandelkern (2019), noticed that this pragmatic solution cannot fully explain the oddness of (ECM). Consider these forms, which I call Yalcin’s conditional and Mandelkern’s disjunction:
-
(YC)
\((p \wedge \Diamond \neg p) \rightarrow \psi \)
-
(MD)
(p ∧♢¬p) ∨ (q ∧♢¬q)
We should agree that sentences like ‘If it is raining and it might not be raining, then it will be sunny tomorrow’ and ‘Either it is raining and it might not be raining, or it is sunny and it might not be sunny’ sound blatantly weird too. But there is an important disanalogy between (ECK) and (ECM), for the former does felicitously embed:
-
(YC)*
\((p \wedge \neg K_{a}p) \rightarrow \psi \)
-
(MD)*
(p ∧¬Kap) ∨ (q ∧¬Kaq)
There is nothing wrong with asserting (say) ‘If it is raining and I don’t know it, then there is something I don’t know’. Disjunctions like ‘Either it is raining and I don’t know it or it sunny and I don’t know it’ are fine too. Pragmatic solutions cannot capture this difference. Even though this pragmatism may explain why asserting the antecedent of (YC)* is weird, it cannot explain why asserting the whole conditional is weird because there is no pragmatic rule which forces us to assert the antecedent whenever we assert a conditional. Thus, the pragmatic solution predicts that (YC) and (YC)* are both fine, which is wrong because the former is not. For similar reasons, the pragmatic solution does not predict the weirdness of (MD). Even if we assert a disjunction, no pragmatic rule forces us to assert at least one disjunct.
3.2 The Semantic Solution
This objection has led recent theorists to argue for a semantic solution. These solutions accept (DES) but reject the classical
consequence that ♢¬p logically entails ¬p. From the proof above it follows that there are only three options for this revisionism: (i) invalidate (CON), (ii) invalidate (CUT), (iii) invalidate (RED).
As far as I know, Mandelkern (2019) is the only one who rejects (CON). However, this move is highly questionable. According to Mandelkern, it is possible to find one context in which ‘It is raining’ is true and ‘It might not be raining’ is true as well although ‘It is raining and it might not be raining’ is false in the very same context. Mandelkern cannot explain this by pointing to a possible context shift happening before the second sentence is uttered. It is just the word ‘and’ that makes the difference. But I urge the reader to check for herself if this is plausible by uttering ‘It is raining. It might not be raining’. No matter how many times I do it, I always get the impression that the second part of my utterance takes back what the first proclaimed. The word ‘and’ does not seem to be the culprit in our case. If this is right, then Mandelkern is mistaken and (CON) is out of bounds.
Rejecting (CUT) in our case is implausible for similar reasons. I do not mean to say that rejecting (CUT) is implausible in general. For instance, Ripley (2013) rejects (CUT) in order to provide a solution to semantic paradoxes like the liar paradox. But in our case the motivation of (CUT)-rejection is hard to see. If there is no relevant difference between the conjunction ‘It is raining and it might not be raining’ and the sentence pair ‘It is raining. It might not be raining’, then we should view the sequence p,♢¬p as problematic if and only if p ∧♢¬p is problematic. Thus, (DES) should be equivalent to the desideratum \(p, \Diamond \neg p \vDash \bot \). But if we insist on the latter desideratum, then just invalidating (CUT) does not profit us anything, for we may derive the absurd conclusion from our new desideratum by invoking (RED) only.
The only remaining solution is to abandon (RED) and it is indeed the most popular route to take in the recent literature. But by taking this path one does face several other important choices and problems. A first challenge for such a solution is to give a semantics which predicts the inconsistency of (MD). It seems fairly clear that a semantic solution to epistemic contradictions should not only be able render (ECM) inconsistent but also the weird disjunction (MD) whose disjuncts are epistemic contradictions. However, some theories on the market—one example is Bledin (2014)—fail to accomplish this task although they successfully manage to render (ECM) semantically inconsistent by invalidating (RED).Footnote 2
Second, only invalidating (RED) threatens (counterintuitively) to validate the inference from p to \(\Box p\). This is odd. Intuitively, there is something wrong with arguments like ‘It is raining. Therefore, it must be raining.’ or ‘She is in New York. Therefore, she necessarily is in New York.’ It seems desirable to have a semantics which invalidates such inferences. But \(p \vDash \Box p\) is conceded in nearly all those theories which provide an anti-(RED)-based semantic solution to epistemic contradictions.Footnote 3 All such theories, however well motivated, leave something important unexplained.
Why is it so popular to just concede the result that p logically entails \(\Box p\)? Because it seems to be the lesser evil. All theories in the anti-(RED) camp have to deal with a dilemma. The reason why this dilemma arises is that the inference from p to \(\Box p\) can be derived from (DES) without invoking (RED) at all. Some stronger non-classical manoeuvre is needed to block this and almost no one is prepared to explain why we should invalidate even more basic principles of classical logic for independent reasons. To see our options, let us start by deriving \(p \vDash \Box p\) from (DES). We need only a few uncontroversial principles to derive \(p, \Diamond \neg p \vDash \neg \Diamond \neg p\) from (DES): (CON), (CUT) and ex absurdo quodlibet (\(\bot \vDash \phi \), for an arbitrary ϕ). But then we can derive \(p \vDash \Box p\) using the law of the excluded middle (LEM), the reflexivity of the consequence relation (REF), the equivalence of ¬♢¬ϕ and \(\Box \phi \) (EQ), and a simple and fairly uncontentious application of reasoning by cases (RC):

Call this result \(\mathcal {D}\). We proceed:

We have not directly relied on (RED) itself. As a consequence, p will be at least as strong as \(\Box p\), which is odd. Given where we are in the dialectic, there seems to be only one possible move to block this reasoning. We have already conceded (DES), (CON), and (CUT) at this point. One cannot reasonably doubt (EAQ), (REF), and (EQ). And while there are information sensitive theories—e.g. the one advocated by Bledin (2014)—which invalidate (RC) if we have modal background assumptions, the only assumption additional to the disjuncts we need in this case is the non-modal atomic assumption p. I’m not aware of any explanation why reasoning by cases should be inadmissible in this case.Footnote 4 If all these principles are unproblematic at this point, then (LEM) is the only possible culprit. In particular, claims of the form ♢¬p ∨¬♢¬p will fail to be logically valid.
To summarize, it seems impossible for anti-(RED) solutions to invalidate the inference from p to \(\Box p\) while keeping every instance of the law of the excluded middle. To give this dilemma a bit more bite, let us briefly turn to both ways of escaping it. First, one might agree with the vast majority and grant \(p \vDash \Box p\). In order to look for an explanation of this seemingly odd inference, one has to consider the specific theories that validate this move. Let us consider but one recent example of such a theory: the assertibility semantics advocated by Hawke and Steinert-Threlkeld (2021). Like many others, they favour a semantics that gives us assertibility conditions relative to a state of information instead of truth conditions relative to a possible world. What is their explanation for the result \(p\vDash \Box p\)? This is not perfectly clear, but they might point out that p seems assertible only if p is settled or known. Since \(\Box p\) just says that p is settled, asserting p yields \(\Box p\) in some sense. But there is still a problem for this strategy. Let us grant that p is assertible (if and) only if the content of p is settled or known. Surely, \(\Box p\) should then be assertible (if and) only if the content of \(\Box p\) is settled or known, i.e. only if \(\Box \Box p\) holds. So, asking whether \(p\vDash \Box p\) holds in an assertibility framework is similar to asking whether \(\Box p\vDash \Box \Box p\) (call this the \(\Box \Box \)-principle of epistemic modality) holds in a truth preservation framework. However, the last claim is not entirely obvious. One might suggest (as, for example, DeRose (1991)) that epistemic modality is at least partly to be analysed in terms of knowledge. If this is right, then the \(\Box \Box \)-principle could turn out as some variant of the KK-principle for knowledge according to which one knows something only if one knows that one knows it (which we can write as \(K_{a}\phi \vDash K_{a}K_{a} \phi \)). But KK is controversial and this controversy might carry over to our debate about epistemic modals.Footnote 5
Additionally, there might be other problems for the specific theory under consideration. According the theory of Hawke and Steinert-Threlkeld, some additional compelling principles of classical logic come out invalid in the modal realm, including disjunction introduction and the DeMorgan laws. Especially the last result is counterintuitive. Hawke and Steinert-Threlkeld (pp. 505-506) explicitly accept and defend the following result:
-
(D)
\(\neg \Diamond p \vee \neg \Diamond \neg p \not \vDash \neg (\Diamond p \wedge \Diamond \neg p)\)
They clarify that (D) arises because ¬♢p ∨¬♢¬p is a logical truth in their system. So, by duality of ‘\(\Box \)’ and ‘♢’ (which they accept - they indeed treat ‘\(\Box \)’ as a mere abbreviation for ‘¬♢¬’), \(\Box \neg p \vee \Box p\) is also a logical truth. But this is naturally taken to be assertible if and only if the information whether p is true is definitely settled, a feature Hawke and Steinert-Threlkeld attribute only to the DeMorganian equivalent ¬(♢p ∧♢¬p). Their so-called explanation for why \(\Box \neg p \vee \Box p\), that is ¬♢p ∨¬♢¬p, is a logical truth—although I am unsure whether they intend to offer an explanation at all—seems to consist only in a quick reference to an alleged intuition to read it as \(\neg p \vee \Box p\) and to a perhaps even more questionable intuition to read the last claim as equivalent to obvious logical truth ¬p ∨ p. This strikes me as a fairly weak kind of reasoning. Similar problems might arise for other theories choosing the first way out of our dilemma.
Take update semantics (US) as another example for a group of theories in this camp. Advocates of (US) theories also endorse \(p\vDash \Box p\). But these theories face other challenges. For instance, Goldstein (2019) provides a recent theory in this tradition which accounts for epistemic contradictions if we augment his basic theory with some additional principles as he suggests. His resulting theory then predicts that p ∧♢¬p is inconsistent. However, it does not predict the inconsistency of ♢p ∧♢¬♢p, which is an instance of ϕ ∧♢¬ϕ. How can it be that some kinds of higher-order epistemic contradictions are fine while the standard (ECM) is not? Goldstein’s specific theory faces a generality problem. Furthermore, all usual (US)-theories—other examples include the theories of Gillies (2004) and Willer (2013)—yield the following results:
-
(a)
\(p \wedge \Diamond \neg p \vDash \bot \)
-
(b)
\(\Diamond \neg p \wedge p \not \vDash \bot \)
They do not, however, validate the inference from ♢¬p to ¬p. But (b) is in doubt. For instance, Mandelkern (2019) emphasizes that the following sentences both sound odd:
-
(a)*#
It is raining and it might not be raining.
-
(b)*#
It might not be raining and it is raining.
The inability to predict the weirdness of (b)* is a not so small shortcoming of (US).Footnote 6
The second route out of our dilemma is to invalidate \(p \vDash \Box p\) while rejecting the law of the excluded middle in its full generality. To my knowledge, Gauker (2021) is the only one who has developed a semantics for this purpose. His semantics is also an assertibility framework, but, unlike Hawke’s and Steinert-Threlkeld’s theory, it validates all the DeMorgan laws and disjunction introduction. Unlike (US)-theories, the order of the conjuncts does not matter: (ECM) and its variant ♢¬p ∧ p are both inconsistent in Gauker’s framework. But it is not without problems. First, his theory validates every instance of (LEM) in a modal-free language but suddenly invalidates some instances in a language containing modals including the relevant instance \(\vDash \Diamond \neg p \vee \neg \Diamond \neg p\) necessary to block the derivation of \(p \vDash \Box p\). But this is odd. Consider these sentences:
-
(i)
Either there is extraterrestrial life or there is no extraterrestrial life.
-
(ii)
Either there might be extraterrestrial life or there cannot be extraterrestrial life.
-
(iii)
Either there possibly is extraterrestrial life or it there necessarily is no extraterrestrial life.
Why is it that (i) is a logical truth while (ii) and (iii) are contingent? Gaukers theory predicts that but I see no intuitive rationale. Second, Gauker only avoids the inference from p to \(\Box p\) but not the inference from \(\Box p\) to \(\Box \Box p\). Perhaps there is still a problem of iteration. In any case, we see that all these revisionary semantic solutions to the problem of epistemic contradictions face challenges that have not been met sufficiently at this point.
4 A Classical Alternative
While they constitute no ultimate knock-down argument, these problems for non-classical treatments suggest that saving classical logic is at least still worth considering. Our problem was that the only classical treatment on the table is the pragmatic solution, which suffers from severe shortcomings. My aim is now to outline a second classical option. I will start by arguing that no solution up to this point has provided a full explanation of the data because even the revisionary semantic solutions need at least one other principle P to account for this. Then I will suggest using principles analogous to P to generalize the story semantics may tell us about (ECM). Provided that we can defend the application of these principles, they will provide the resources to explain all the data. In Sections 4.4–4.7 I will show how these principles can dissolve our problem without sacrificing classical logic.
4.1 The Need for an Additional Principle
The first step to do is to compare instances of (YC) to conditionals with contradictory antecedents:
-
(CA)#
If it is raining and it might not be raining, then it will be sunny tomorrow.
-
(CB)#
If it is raining and it is not raining, then it will be sunny tomorrow.
Both are puzzling, regardless of what their semantic value is. But even for (CB) the cause of this cannot be a contradictory status of the sentence itself. According to most theories of conditionals—and that includes classical logic –, a conditional with a contradictory antecedent is not a logical falsity but a logical truth. However, logical truths are usually not weird in the same sense, albeit uninformative. Even if we were to classify the antecedents of the Yalcin-conditional (CA) and (CB) as inconsistent, we would still need one additional step to explain the oddness of the conditionals.
Surely, the obvious principle to use is If the antecedent of a conditional is inconsistent, then the whole conditional is weird. We can bolster this principle by referring to the classic idea of Ramsey (1931) that conditionals are evaluated by assuming the antecedent. And contradictions cannot be assumed, so our evaluation fails at some point. But I want to suggest that this explanation might also works for more cases than contradictions. Maybe (ECM) cannot be assumed either. We can use a more general and perhaps weaker principle to account for this case: If the antecedent of a conditional is weird, then the whole conditional is weird. This is our principle P and it is all we need. The weirdness need not be a contradictory status. It is an epistemic weirdness that reflects our inability to grasp (i.e. our inability to assume) the content of the sentence. If our imaginativeness fails us, so to speak, when we consider the antecedent, we cannot properly evaluate the whole conditional.
True, P is only for the conditional, but if we need to invoke it for conditionals, then we have some reason to believe that we should invoke similar principles for disjunction, conjunction, and all other sentential operators. Maybe we even epistemically evaluate disjunctions by assuming each disjunct, and we cannot grasp the content of a disjunction if we can assume neither disjunct. If this is right, then the relevant principles for weirdness projection will see to it that the defective epistemic status adequately generalizes to (YC) and (MD). The task is yet to argue that (ECM) really has this feature of basic epistemic defectiveness, although (ECK) does not. Then we need to make the theory of epistemic weirdness sufficiently precise and general.
4.2 (ECM) Cannot Be Imagined
A difference in epistemic status between (ECK) and (ECM) is not difficult to find. Comparing (ECM) and (ECK), we can see that these sentences differ on the epistemic level of assuming their contents. To check this, try to imagine for a moment that it is raining but you don’t know this. No problem? Then try now to imagine that it is raining but it might not be raining. You cannot do it? Yes, (ECM) is just like a contradiction in the sense that we cannot imagine how a situation looks like in which it is true.Footnote 7 But there is more to our ability to imagine certain things than the semantic status. We are talking about an epistemic status. Our notion of knowledge plays some role here. Whenever we imagine ϕ being true, it should be at least possible—in a very loose sense of ‘possible’—to know that ϕ is true. I suggest using logical possibility for our purpose here, which yields the following imaginability contraint:
-
(IC)
ϕ is imaginable only if it is logically possible that there is an agent A such that A knows that ϕ is true.
We may also say that we must in principle be able to switch to a perspective from which the sentence under discussion is true. Imagining/assuming/ supposing/entertaining involves knowledge from a perspective. It is certainly logically possible that an agent knows the content of (ECK)—p ∧ Kap. Save for the referent of a we may pick any agent we like to serve as the perspective we need.
However, things are different when we consider (ECM). I believe that no logically possible agent can know that p ∧♢¬p is true. The reason is that the epistemic possibility operator in some sense includes the viewpoint of the assessor. Because the most salient assessor in a context is usually the speaker, one might endorse what Egan et al. (2005) call the speaker-inclusion constraint for epistemic modals: the relevant community for a semantic evaluation of epistemic modal-claims includes the speaker. Not everyone accepts this constraint, though. Relativists like MacFarlane (2011) conclude that assessing statements of epistemic modality is not necessarily tied to the speaker. But my theory can remain neutral about this particular constraint. All we need is that epistemic modals include the evaluating perspective. After setting up my theory in Sections 4.4–4.6 I will come back to this point.
4.3 Hypothetical Agents
Before I develop my theory, there is one objection we must consider immediately for it threatens the very foundations of the theory. This objection concerns the (IC)-idea that imagining ϕ is possible only if some logically possible agent knows that ϕ is true. Consider this sentence:
-
(YC)+ If it is raining and no one knows that it is raining, then no one will be prepared.
Can the antecedent of (YC)+ be imagined? Yes, no problem. This conditional is not odd at all. But my theory doesn’t seem to predict that. I have said that you can imagine ϕ being true only if there is a logically possible agent who knows that ϕ is true. But there is no logically possible agent who knows that ‘It is raining and no one knows that it is raining’ is true. The sentence itself states that no agent knows that it is raining, but any agent who knows that it is raining and no one knows that it is raining also knows that it is raining. Thus, no agent can know the antecedent of (YC)+ and by my theory we arrive at the false result that we cannot imagine it.
However, there is a way out. What this objection shows is that we need to be careful how to talk about perspectives. The claim that imagining is related to the knowledge of an agent is misleading to quite some extent. We usually take agents to be things we can refer to and quantify over. If something is an agent, then it should be in the domain of ‘no one’ or ‘no agent’ (at least in some context). But the agents used to explain the notion of imagining or assuming are different. These are hypothetical or ideal perspectives we cannot refer to. ‘It is raining and no one knows that it is raining’ cannot be known by A if A is a member of the domain of ‘no one’. But the relevant A here is meant to be a purely hypothetical perspective. ‘No one’ ranges over the set of all (contextually relevant) actual agents and does not include the viewpoint of a hypothetical perspective.
Thus, my theory can still predict that the antecedent of (YC)+ is imaginable. It is still knowable from a hypothetical perspective. Next, I will show how we can achieve this result within a precise and classical semantic framework.
4.4 Models
Apart from the usual operators, we will add K. to our formal language and introduce individual constants a (and variables) as arguments for this operator and a universal quantifier for them. But although we use individual constants and quantifiers for this purpose, I only consider the propositional fragments of the language otherwise. Following Kaplan (1989), I provide a two-dimensional semantics comprising a context c and an index which will just be a world of evaluation w. The other parameters are standard in multi-agent epistemic logic. A model \({\mathscr{M}}\) for the language will be a quadruple 〈W,A,C,I〉 such that:
-
(1)
W is a (non-empty) set of possible worlds w,
-
(2)
A is a (non-empty) set of possible agents α,
-
(3)
C is a (non-empty) set of contexts c, and
-
(4)
I is the following evaluation function for atomic sentences: AT × C × W↦{0,1} (where AT is the set of atomic sentences 1 and 0 are our truth values).
When we speak of contexts, the question arises what this entity is supposed to be. What sort of things does a c ∈ C provide? The quick answer is: a lot. For present purposes, I take it to include these things:
-
Ac is a (non-empty) subset of A and represents the set of all relevant actual agents in c.
-
\({A_{c}^{i}}\) is a (possibly empty) subset of A and represents the set of all relevant hypothetical agents or perspectives in c.
-
Dc is the context’s denotation function that assigns to each individual constant a a member of Ac.
-
Rc is the agent-relative accessibility relation of c. Formally: \(R_{c} \subseteq A_{c}\cup {A_{c}^{i}} \times W\times W\). Instead of writing 〈α,w,v〉∈ Rc we may also use the abbreviation wRc,αv meaning that v is accessible from w for the agent α in context c .
-
As a constraint we postulate that for all c ∈ C: Rc is reflexive in the following sense: \(\forall \alpha \in A_{c}\cup {A_{c}^{i}}\) ∀w ∈ W : wRc,αw.
-
-
wc ∈ W is the world of c.
The agent-relativity and reflexivity of the accessibility relation are standard in multi-agent epistemic logic. Here we just restrict it to the contextually relevant agents. The other ingredients of the contexts will hopefully become clearer if we turn to the truth conditions.
4.5 Truth conditions
First, we need to focus on the basic truth conditions. The clauses for the truth valuation function V for the connectives are standard:
-
(I)
\(V_{{\mathscr{M}}, c, w}(p) = 1\) iff I(p,c,w) = 1
-
(II)
\(V_{{\mathscr{M}}, c, w}(\bot ) = 1\) iff 1 ≠ 1
-
(III)
\(V_{{\mathscr{M}}, c, w}(\neg \phi ) = 1\) iff \(V_{{\mathscr{M}}, c, w}(\phi ) = 0\)
-
(IV)
\(V_{{\mathscr{M}}, c, w}(\phi \wedge \psi ) = 1\) iff \(V_{{\mathscr{M}}, c, w}(\phi ) = 1\) and \(V_{{\mathscr{M}}, c, w}(\psi ) = 1\)
-
(V)
\(V_{{\mathscr{M}}, c, w}(\phi \vee \psi ) = 1\) iff \(V_{{\mathscr{M}}, c, w}(\phi ) = 1\) or \(V_{{\mathscr{M}}, c, w}(\psi ) = 1\)
-
(VI)
\(V_{{\mathscr{M}}, c, w}(\forall x\phi ) = 1\) iff \(V_{{\mathscr{M}}, c, w}(\phi _{[a/x]}) = 1\) for an arbitrary individual constant a, where ϕ[a/x] is the formula resulting from ϕ by replacing all the free occurrences of x in ϕ by a.Footnote 8
Before we introduce the conditions for the knowledge operator, we define the notion of an information state S of some agent α ∈ A relative to some context c and some world w:
(DEF1): \(S_{{\mathscr{M}}, c , w}(\alpha )\) = {v ∈ W | wRc,αv}
Thus, the accessibility relation provides the information state for each agent. It is the set of all worlds the agent may access. Using this definition, we may now state the clause for the knowledge operator:
-
(VII)
\(V_{{\mathscr{M}}, c, w}(K_{a} \phi ) = 1\) iff for all \(w^{\prime } \in S_{{\mathscr{M}}, c, w}(D_{c}(a))\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi ) = 1\)
Now our task is to state the truth conditions for epistemic modals. But the domain for these modals is controversial. One possibility, mentioned by philosophers like Teller (1972), is to take the domain of epistemic modals to be the combined knowledge of the agents in the context of utterance. In other words, the modal domain will be the intersection of all the information states of all the agents. One advantage of this view, as many authors have noticed, is that we can explain how people can disagree by uttering sentences of the form ‘X is possible’ and ‘X is not possible’, whereas a theory according to which statements of epistemic possibility are only relative to the knowledge of the speaker cannot account for this. Footnote 9 However, I do not claim that there cannot be other ways to implement the key thoughts. In particular, I do not mean to take a stance on what the relevant actual agents are in ordinary conversations. For instance, it is irrelevant for the present solution whether the speaker is always relevant is the right sense. I will leave the notion of relevant agents unexplained. Here is the definition of the modal domain as the combined information state of all the relevant agents relative to some context and world of evaluation:
(DEF2): \({\varDelta }_{{\mathscr{M}}, c, w} = \{ v \in W\) | \(\forall \alpha \in A_{c} \cup {A_{c}^{i}}: wR_{c, \alpha } v\}\)
This yields the following truth conditions:
-
(VIII)
\(V_{{\mathscr{M}}, c, w}(\Box \phi ) = 1\) iff for all \(w^{\prime } \in {\varDelta }_{{\mathscr{M}}, c, w}\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi ) = 1\)
-
(IX)
\(V_{{\mathscr{M}}, c, w}(\Diamond \phi ) = 1\) iff there is at least one \(w^{\prime } \in {\varDelta }_{{\mathscr{M}}, c, w}\) such that \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi ) = 1\)
It is tempting to simplify this proposal like this: ‘must(A)’ really means the same as ‘A is entailed by the set of propositions known by somebody in the group’. This is indeed almost right. If I know A, then A is entailed by the set of propositions known by somebody in the group that includes me. My knowledge always gets transferred to the combined knowledge if I am relevant. So, I can never truly say something like ‘I know it’s raining but it might not be raining’. This will always be false if the speaker is relevant (which one might think is always the case).
However, this simplifying proposal is not entirely right. True, what someone (who is relevant) knows is also combined knowledge. But that does not mean that the combined knowledge consists only of those propositions known by someone. Consider a case where Andrew knows A, Barbara knows B, and Charlie knows C. Assume that D logically follows from A, B, and C taken together but D does only follow if you have all of A, B, and C as premises. In this case, it might very well be that neither Andrew nor Barbara nor Charlie knows D. But relative to the whole group of them D will still be combined knowledge. Thus, someone’s knowing A is sufficient but not necessary for A becoming combined knowledge.Footnote 10
4.6 Validity and Results
The next step is to define the validity relation. Following Kaplan (1989), we may first define truth in a context:
-
(TC)
ϕ is true relative to a model \({\mathscr{M}}\) and a context c ∈ C iff \(V_{{\mathscr{M}}, c, w_{c}}(\phi ) = 1\).
Now we may define logical validity for this theory T:
-
(VAL)
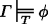 iff there is no model \({\mathscr{M}}\) and no context c ∈ C such that for all γ ∈Γ: γ is true relative to \({\mathscr{M}}\) and c and ϕ is not true relative to \({\mathscr{M}}\) and c.
iff there is no model \({\mathscr{M}}\) and no context c ∈ C such that for all γ ∈Γ: γ is true relative to \({\mathscr{M}}\) and c and ϕ is not true relative to \({\mathscr{M}}\) and c.
Before I continue with the part of the theory that explains epistemic contradictions, let me briefly summarize the most important results.
-
(R1)
\(\neg \Box \phi \) is semantically equivalent to ♢¬ϕFootnote 11
-
(R2)
\(\Box \neg \phi \) is semantically equivalent to ¬♢ϕ
(R3)]
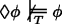
(R4)]
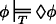
(R5)]
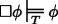
(R6)]
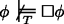
(R7)]
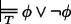
(R8)]
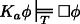
(R9)]
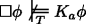
(R1)–(R6) secure the fundamental principles of epistemic modal logic and (R7) saves the law of the excluded middle. (R1) and (R2) yield the duality of ‘\(\Box \)’ and ‘♢’. (R3)–(R6) are general principles clarifying the strength of the necessity and the possibility operator. In particular (R6) and (R7) make sure that the present theory doesn’t face the problems recent non-classical solutions which invalidate (RED) have to deal with. (R8) and (R9) are of particular interest, for they illuminate the relation between knowledge and epistemic necessity. Although knowledge implies necessity according to (R8), it is perfectly consistent to maintain that something is (epistemically) necessary although one does not know it. Epistemic necessity does not even entail, as mentioned above, that someone knows. The theory even predicts the behaviour of higher-order modality and explains some complex interactions between knowledge and epistemic modality. For instance, we can prove that \(\Box \phi \) does not entail \(\Box \Box \phi \) and that \(\Diamond \Box \phi \) does not entail \(\Box \phi \). We may also show that ♢Kaϕ and Ka♢ϕ do not entail each other. Everything is classical.
4.7 Epistemic Weirdness
Since the semantics is clear by now, we can proceed with the explanatory task. I am now going to define what it means for a sentence to have a defective epistemic status. Above, I talked about our inability to imagine or assume the truth of certain sentences. Now I will call an epistemically defective sentence epistemically weird (short: e-weird) to have a more artificial term. But the intuitive story remains: being e-weird means that it is not imaginable what content the sentence has. Not being imaginable means either i) that the content of the sentence is unknowable (captured by the (IC)-principle above) or ii) that the sentence is built up in a certain way from other sentences whose content is unknowable.
Before I state the theory precisely, it is worth pointing out that this disjunctive nature of imaginability will lead to the result that e-weirdness is not closed under logical consequence. Consider the following result of the semantics:
-
(R10)
(p ∧♢¬p) ∨ (¬p ∧♢p) is semantically equivalent to ♢p ∧♢¬p.
Since (p ∧♢¬p) ∨ (¬p ∧♢p) is a Mandelkern disjunction, it should be e-weird. But ♢p ∧♢¬p should not. We can perfectly imagine what it means to say ‘It might be raining and it might not be raining’. Neither weirdness nor non-weirdness is preserved by logical consequence because certain sentences do indeed have a different weirdness status and yet they are semantically equivalent.Footnote 12
A related point is that a claim like Kaϕ can be true, although ϕ is an e-weird sentence. (p ∧♢¬p) ∨ (¬p ∧♢p) should be e-weird. But the reason for this need not be that we cannot know its content. Indeed, we can know it because we can know the content of ♢p ∧♢¬p which is by (R10) exactly the same. We can also know that their contents are the same by using some logical deduction. If we do some logic and thereby come to know that (p ∧♢¬p) ∨ (¬p ∧♢p) and ♢p ∧♢¬p are equivalent, then our knowledge of the content of ♢p ∧♢¬p will secure that we know the content of (p ∧♢¬p) ∨ (¬p ∧♢p).
Now let us move to the precise theory. We will start with the clause that unknowability yields e-weirdness:
-
(C1)
If there is no model \({\mathscr{M}}\), no c ∈ C, no w ∈ W and no \(\alpha \in A_{c} \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi ) = 1\), then ϕ is e-weird.
If there is absolutely no context in which any relevant agent—who might be a completely invented hypothetical agent—may know that ϕ, we cannot imagine ϕ being true.Footnote 13 In such a case, ϕ will be e-weird. This clause delivers the desired result that standard epistemic contradictions of the form ϕ ∧♢¬ϕ are e-weird. Footnote 14 But this is only a start. I said we have some reasons to believe that we need projection rules for the sentential operators including the conditional. The rules for conjunction, disjunction and conditionals (→) are these:
-
(C2)
If ϕ is e-weird or ψ is e-weird, then ϕ ∧ ψ is e-weird.
-
(C3)
If ϕ is e-weird and ψ is e-weird, then ϕ ∨ ψ is e-weird.
-
(C4)
If ϕ is e-weird, then \(\phi \rightarrow \psi \) is e-weird.
I have not provided the truth conditions for sentences of the form \(\phi \rightarrow \psi \), but there is no need to state them to achieve the desired results. The actual truth conditions or assertibility conditions for the indicative conditional are controversial and I do not intend to contribute to that discussion here. From an epistemic point of view, we evaluate conditionals by first considering (that is imagining or assuming) the antecedent. This is all we need. The concept of e-weirdness is not (directly) about truth or falsity, but about our evaluating or entertaining certain propositions. All we need is to maintain that we must be able to entertain the antecedent of a conditional to make sense of the whole thing. Those who wish to defend the truth-functional material conditional analysis as the correct approach to the semantics of indicative conditionals may assume that \(\phi \rightarrow \psi \) is semantically equivalent to ¬ϕ ∨ ψ.
The job of (C3) and (C4) is, of course, to deliver the e-weirdness of (YC) and (MD). (MD) is weird because if we want to entertain a disjunction epistemically, we consider each disjunct separately, asking ourselves what it may mean. If you consider a disjunction like ‘Either the first sentence in Cicero’s lost dialogue Hortensius is true, or it is not the case that the first sentence in Cicero’s lost dialogue Hortensius is true’ this is no problem because you can perfectly imagine the truth (and the falsity) of each disjunct. Since you know the truth conditions for disjunction, you have no problem knowing that the disjunction is true, although you don’t know whether the first or the second disjunct is true. Cicero’s Hortensius is lost, after all. However, when you encounter a disjunction neither disjunct of which you understand properly (because you can imagine neither of them being true) it leaves you puzzled. This simple fact is all we need to motivate (C3).
But one might ask at this point why we shouldn’t have even stricter clauses. For example, one might want to replace (C3) with the following alternative:
-
(AC3)
If ϕ is e-weird or ψ is e-weird, then ϕ ∨ ψ is e-weird.
(AC3) also delivers the e-weirdness of the following kind of disjunction:
-
(MD)*
Either it is raining and it might not be raining, or it is sunny.
It is, however, not clear to me whether it is desirable to render (MD)* e-weird. But I agree that (MD)* still seems strange. (AC3) might be the right way to go after all.Footnote 15 However, in what follows I will assume the weaker (C3) instead of (AC3).
Here are the next clauses for the theory of e-weirdness:
-
(C5)
If ϕ is e-weird, then Kaϕ is e-weird (for any individual constant a).
-
(C6)
If ϕ contains an individual constant a and ϕ is e-weird, then ∀vϕ[v/a] is e-weird (for any variable v where ϕ[v/a] is the sentence resulting from replacing all the occurrences of a in ϕ with v).
-
(C7)
If ϕ is e-weird, then \(\Box \phi \) is e-weird.
-
(C8)
If ϕ is e-weird, then ♢ϕ is e-weird.
A major problem left is to deal with negation. E-weirdness does not project through negation. Take any logical falsity and apply the negation operator and you will get a logical truth. But while we intend to claim that logical falsities are e-weird, we do not want to say the same about logical truths. A way to illuminate the situation is to think about sentences with (semantic) presupposition failure because they too cannot be imagined, provided that we restrict the discussion to contexts where the presupposition fails. It is apparent since Russell (1905) that applying the negation operator to sentences with presupposition failure need not result in an equally weird claim because there is a way to make sense of the negation. Russell’s famous example ‘The present king of France is not bald’ sounds fine if we take this to say that there is no present king of France.
Whatever the correct analysis is, negation shifts our ways of thinking about a weird sentence. Provided that there is no present king of France, ‘The present king of France is bald’ is not true while ‘The present king of France is not bald’ is not false (as far as natural language is concerned).Footnote 16 We can say the same about logical falsities and logical truths. E-weirdness only tells us half the story. This notion explains the epistemic status of contradictions, but it does not explain the status of logical truths. While we cannot imagine logical falsities being true, we cannot imagine logical truths being false. We may construct another notion that captures this last status and generalize it by applying perfectly symmetrical rules. But this other notion applies not only to logical truths. Here is another example:
-
(EX)
Either it is not raining or it must be raining.
For some native speakers (EX) presumably looks like a logical truth, but it isn’t, at least according to orthodoxy and the present theory. This appearance is inter alia caused by the impossibility to imagine it being false. For lack of a better term, we may call this other notion epistemic-contra-weirdness (short: e-c-weirdness). Here are the rules:
-
(C1)*
If there is no model \({\mathscr{M}}\), no c ∈ C, no w ∈ W and no \(\alpha \in A_{c} \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w}(\phi ) = 0\), then ϕ is e-c-weird.
-
(C2)*
If ϕ is e-c-weird and ψ is e-c-weird, then ϕ ∧ ψ is e-c-weird.
-
(C3)*
If ϕ is e-c-weird or ψ is e-c-weird, then ϕ ∨ ψ is e-c-weird.
-
(C4)*
If ψ is e-c-weird, then \(\phi \rightarrow \psi \) is e-c-weird.
-
(C5)*
If ϕ is e-c-weird, then Kaϕ is e-c-weird (for an arbitrary individual constant a).
-
(C6)*
If ϕ contains an individual constant a and ϕ is e-c-weird, then ∀vϕ[v/a] is e-c-weird (for any variable v where ϕ[v/a] is the sentence resulting from replacing all the occurrences of a in ϕ with v).
-
(C7)*
If ϕ is e-c-weird, then \(\Box \phi \) is e-c-weird.
-
(C8)*
If ϕ is e-c-weird, then ♢ϕ is e-c-weird.
Now we are ready to deal with negation. Negation just transforms an e-weird sentence into an e-c-weird sentence and vice versa:
-
(C9)
If ϕ is e-c-weird, then ¬ϕ is e-weird.
-
(C9)*
If ϕ is e-weird, then ¬ϕ is e-c-weird.
Finally, we provisionally finish up the definition of e-weirdness and e-c-weirdness by stating the end-clauses:
-
(END)
Nothing else other than specified by the clauses (C1)–(C9) is e-weird.
-
(END)*
Nothing else other than specified by the clauses (C1)*–(C9)* is e-c-weird.
This theory of epistemic weirdness yields the following results:
-
(R11)
If for every \({\mathscr{M}}\), every c ∈ C and every w ∈ W: \(V_{{\mathscr{M}}, c, w}(\phi ) = 0\), then ϕ is e-weird.
-
(R12)
If for every \({\mathscr{M}}\), every c ∈ C and every w ∈ W: \(V_{{\mathscr{M}}, c, w}(\phi ) = 1\), then ϕ is e-c-weird.
-
(R13)
ϕ ∧♢¬ϕ is e-weird.
-
(R14)
♢¬ϕ ∧ ϕ is e-weird.
-
(R15)
\((\phi \wedge \Diamond \neg \phi ) \rightarrow \psi \) is e-weird.
-
(R16)
(ϕ ∧♢¬ϕ) ∨ (ψ ∧♢¬ψ) is e-weird.
-
(R17)
p ∧¬Kap is not e-weird.
-
(R18)
p ∧∀x¬Kxp is not e-weird.
The results are as desired.Footnote 17 The first result shows that all contradictions are e-weird, while the second ensures that all logical
truths are e-c-weird. (R13) and (R14) explain the basic problem of epistemic contradiction while (R15) and (R16) generalize the explanation to Yalcin’s conditional and Mandelkern’s disjunction. (R18) shows that we escape the problem mentioned in Section 4.3. Importantly, (R17) and (R18) mark the difference between (ECM) and (ECK). The latter is not weird in our sense. To explain the weirdness of (ECK) where the relevant knowledge is the knowledge of the speaker, we may resort to the standard pragmatic explanation for (ECK). We may prove that there is no model \({\mathscr{M}}\), no c ∈ C, no w ∈ W and no \(\alpha \in A \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w}(\phi \wedge \neg K_{a}\phi ) = 1\) provided that we choose α such that Dc(a) = α. Dc(a), i.e. the relevant knowing person, cannot know the content of (ECK). This explains its partial weirdness.
5 On Some Worries
Let me finish by briefly addressing some worries one might have about this theory of epistemic weirdness. First, one might still worry that the solution provided by the theory is hopelessly ad hoc. Without the clauses for the conditional and disjunction, we could not prove the weirdness of (YC) or (MD). Since epistemic weirdness is about knowledge in some sense and since knowledge does not distribute over disjunction, it seems particularly ad hoc to introduce the disjunction clause just to explain (MD). What can I say?
First, to repeat what I have said above, we simply need an additional principle for conditionals to explain the weirdness of (YC), and the principle provided above is as worthy as the common principle that conditionals should not have a contradictory antecedent. Second, the notion of epistemic weirdness is per se not about the semantics. We do not ask what the truth conditions of a sentence ϕ are or what it means to say that ϕ follows logically from a set of sentences. We just ask whether we can imagine what ϕ means. The mistake is to assume that questions about epistemic entertaining and the semantics are equivalent. Most likely the semantics is involved to some extent in our epistemic sense-making, but there is no need to assume that questions about epistemic sense-making are always fully equivalent to some questions about the semantics. We bolster the clauses for disjunction, conjunction, the conditional, and for the modal operators not by invoking semantic principles. The questions ‘Can ϕ be true?’ and ‘Can we epistemically entertain ϕ being true’? are different.
Here is another way of thinking about it. In his recent book on conditionals, Williamson (2020) argues that the classical truth-functional semantics for the indicative conditional is actually correct. The claim ‘If you fall, you’ll hurt yourself’ is true if and only if either you do not fall or you’ll hurt yourself. According to Williamson, our intuition that there are insurmountable obstacles to the truth-functional analysis can be explained by referring to our heuristics for evaluating conditional sentences. Assuming the antecedent and thinking about the consequent under this assumption is the most important heuristic. These heuristics may be useful, but if Williamson is right, they do not work in every case and face certain insurmountable challenges of their own. Williamson’s distinction between heuristics and semantics can be applied to our problem. In this terminology, we may say that the various truth-conditional clauses reflect the semantics and the clauses for epistemic weirdness (partially) reflect our heuristics. We may say that epistemic weirdness arises if our evaluation heuristics do not lead to a proper verdict. We may call this heuristic failure. One reason for heuristic failure is that the semantic status of the sentence in question is itself defective. But in some cases of heuristic failure the semantic status might be just fine.
Another worry concerns the testability of the theory.Footnote 18 The theory introduces hypothetical agents which makes it not obvious how the theory can be tested. One might worry, for instance, that the presence of hypothetical agents can be used as a cheap move to account for empirical data. But I don’t think this is a huge problem. There is a straightforward way to test the theory in ordinary conversations. In such conversations we typically are in a context that can be called actual. A context is defined to be actual iff the set of hypothetical agents is empty. These hypothetical agents are auxiliary constructions to help us make sense of certain claims. But in ordinary conversations we should suppose that only actual agents are present.Footnote 19 The fact that we cannot quantify over hypothetical agents also has no obvious shortcomings.Footnote 20
Here is the final worry I want to address: Even if this generalization strategy for epistemic weirdness is correct, why can’t we use a different base clause? Many non-classical theories may provide an adequate base clause. Any theory validating \(p \wedge \Diamond \neg p \vDash \bot \), may provide the following base clause:
If \(\phi \vDash \bot \), then ϕ is e-weird.
We still need the corresponding clause for e-c weirdness, but the obvious candidate to use here is:
If \(\neg \phi \vDash \bot \), then ϕ is e-c-weird.
I have no objections to such a proposal. It might turn out that various semantic theories may provide an adequate alternative base clause to (C1) above and that is fine by me. The semantics I presented above is just one suggestion to solve the problem without sacrificing classical logic. The standard pragmatic solution to epistemic contradictions is inadequate because it does not capture the difference between (ECK) and (ECM) and solutions that invalidate (CON) or (CUT) are either implausible or useless. But I do not claim that either different classical conceptions or revisionary solutions that invalidate (RED) cannot provide a reasonable alternative by using the projection clauses of epistemic weirdness. My claim is that these revisionary solutions are not necessary to solve the puzzle of epistemic contradiction. But by using the projection clauses for epistemic weirdness they may very well be sufficient.
6 Conclusion
I have outlined the puzzle of epistemic contradiction, and I considered various solutions. There are those who see epistemic contradictions as ordinary semantic contradictions and those who do not want to admit this. Each group faces challenges of their own, and the debate remains in flux. In this paper, I have presented an alternative theory by which one may allay many of these worries. As neither semantic nor standard pragmatic explanations seem to be without shortcomings, we should rather locate the problem at the epistemic level. Epistemic contradictions have a defective epistemic status, but this is consistent with the claim that their semantic status is unproblematic.
Code Availability
Not applicable
Notes
Although this last step might be contested, I assume for the sake of the argument that it holds. See DeRose (1991, pp. 596–599) for a defence.
Punčochár and Gauker (2020, p. 674) attribute the observation that Bledin’s semantics does not yield the inconsistency of (MD) to Ivano Ciardelli.
Among those theories are those using a version of update semantics like those of Gillies (2004), Willer (2013), and Goldstein (2019), as well as the informational semantics of Bledin (2014), the inferential-expressivist framework of Incurvati and Schlöder (2019), the expressivistic assertibility semantics of Hawke and Steinert-Threlkeld (2021), and the attitude semantics of Ciardelli(2021).
It is true, however, that proof by cases is in general not admitted as a valid rule in information sensitive systems. They in general also validate (LEM) while invalidating the must excluded middle \(\Box \phi \vee \Box \neg \phi \). However, it does not really matter for this point since, as mentioned above, these systems also predict that ϕ really does entail \(\Box \phi \). Also, the must excluded middle does not strike me as a very plausible principle from the outset. Thanks to an anonymous reviewer for asking me to clarify this.
For an argument that KK is inconsistent with knowledge externalism see Bird and Pettigrew (2021). The most influential argument against KK is given in Williamson (2000, Ch. 5). It is true, however, that Williamson’s argument from margin for error principles does not directly carry over to the realm of epistemic modality because no one has yet identified analogous margin for error principles for epistemic modals with a comparable level of intuitive plausibility, as an anonymous reviewer pointed out to me. What is more, there are also recent defences of KK: see Dorst (2019), Das and Salow (2018), and Stalnaker (2015). Thus, the problem for the \(\Box \Box \)-principle, if there is any, is certainly not the most cogent one.
I say ‘inability’ although this is not that clear. Beddor and Goldstein (2018, p. 105) offer another solution for the infelicity of (b)*: Just like (a)* the sentence is never assertible or fully true, in the sense that there is no information state which entails (a)* or (b)*. However, this solution still predicts that the semantic status of (a)* and (b)* are different (one is consistent while the other is not) and it remains unclear whether ordinary speakers may track this difference. See Mandelkern (2019) for more discussion and criticism of (US)-approaches to this problem.
We assume for these substitutional semantics that for every context c and for every α ∈ Ac there is a constant a such that Dc(a) = α.
At this point I should also say that some alternative conceptions will not work for my purpose. For example, it will not do to define the modal domain as the union of all the propositions known by some agent. On that view ‘must(A)’ is true iff all members of the group know A. Consequently, ‘might(A)’ will be true iff some agent does not know A. But these truth conditions for ‘might(A)’ are too weak to adequately explain (ECM). On that proposal (ECM) can be known by some agents. Say Barbary knows that it is raining but Peter doesn’t. Then Barbara will be able to know that it is raining but it might not be raining. This strikes me as odd and it is certainly not compatible with the explanation I want to give. Thanks to an anonymous reviewer for pressing me to clarify this.
Again I owe the discussion of this proposal to an anonymous reviewer.
Two sentences ϕ and ψ are defined to be semantically equivalent if and only if: for every model \({\mathscr{M}}\), every c ∈ C and every w ∈ W: \(V_{{\mathscr{M}}, c, w}(\phi ) = 1\) if and only if \(V_{{\mathscr{M}}, c, w}(\psi ) = 1\).
This is, however, only due to the fact that e-weirdness does not coincide with unknowability. Unknowability itself, as specified by (C1) below, is closed under logical equivalence. Thus, if ϕ and ψ are equivalent but have a different weirdness status, this can only be because one but not the other is built from sentences with an unknowable content.
I should perhaps point out a potentially misleading usage of the term ‘unknowability’. I use the term ‘unknowability of ϕ’s content’ loosely for the antecedent of (C1). If ϕ has this feature, then the sentence Kaϕ will be false in every context for every agent picked out by ‘a’. But there is a sense of ‘knowable’ in which even the content of epistemic contradictions might be knowable. In my use of ‘unknowability’ I assume a certain kind of contextual stability for the relevant interpretation of ‘knowledge’. My framework does not relativize the knowledge operator to a particular context (only the whole sentence is relativized to a context). An anonymous reviewer asked me whether the content of a sentence of the form ϕ ∧♢¬ϕ couldn’t be known from another context. In a context c where A and B are the only agents and B utters ’It is raining but it might not be raining’, what B said cannot be known by either A or B. But, so goes the suggestion, we might engage in a meta-level talk in which we relativize knowledge to contexts too. If C is an agent of a new context c\(^{\prime }\), couldn’t C know in c\(^{\prime }\) that what B said in c is true in c (even if B uttered an e-weird sentence in c)? What if C does know in c\(^{\prime }\) that it is raining in c and that the combined knowledge of A and B in c does not entail that it is raining in c? I agree that C can know this in c\(^{\prime }\). If we allow for this cross-contextual knowledge talk, then the content of e-weird sentences becomes knowable from another context. But even if my label ‘unknowability’ is then misleading in the sense used, the result that we can know from a certain context what another agent said in another context by uttering an epistemic contradiction strikes me as correct from the contextualist’s point of view.
Proof
To facilitate the proof a little bit let us first prove a useful lemma:
-
(L)
For every model \({\mathscr{M}}\), every c ∈ C, every w ∈ W, and every \(\alpha \in A_{c} \cup {A_{c}^{i}}\): \({\varDelta }_{{\mathscr{M}}, c , w} \subseteq S_{{\mathscr{M}} , c , w}(\alpha )\)
Here is the proof for (L): Take an arbitrary model \({\mathscr{M}}\), a c ∈ C, a w ∈ W, and an arbitrary \(\alpha \in A_{c} \cup {A_{c}^{i}}\). Now take an arbitrary x ∈ W and assume (1) \(x \in {\varDelta }_{{\mathscr{M}}, c , w}\). We show that \(x \in S_{{\mathscr{M}} , c , w}(\alpha )\). First, it follows from 1 by definition that (2) ∀α*\( \in A_{c} \cup {A_{c}^{i}}: wR_{c, \alpha ^{*}} x\). 2 directly entails wRc,αx and we conclude per definition that \(x \in S_{{\mathscr{M}} , c , w}(\alpha )\).
Now we are ready to prove that ϕ ∧♢¬ϕ is e-weird. Assume for reductio that there is a model \({\mathscr{M}}\), a c ∈ C, a w ∈ W, and an \(\alpha \in A_{c} \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi \wedge \Diamond \neg \phi ) = 1\). This entails (i) for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi ) = 1\), and (ii) for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\Diamond \neg \phi ) = 1\). The reflexivity constraint for Rc ensures that wRc,αw. Thus, \(w \in S_{{\mathscr{M}}, c , w}(\alpha )\). By ii we may now conclude that \(V_{{\mathscr{M}}, c, w}(\Diamond \neg \phi ) = 1\). Thus, there is a \(w^{\prime \prime } \in {\varDelta }_{{\mathscr{M}}, c , w}\) such that \(V_{{\mathscr{M}}, c, w^{\prime \prime }}(\neg \phi ) = 1\). Call this \(w^{\prime \prime }\) w∗. So \(V_{{\mathscr{M}}, c, w^{*}}(\neg \phi ) = 1\) which means \(V_{{\mathscr{M}}, c, w^{*}}(\phi ) = 0\). By i and (L) we conclude that for all \(w^{\prime } \in {\varDelta }_{{\mathscr{M}}, c , w}\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi ) = 1\). But since \(w^{*} \in {\varDelta }_{{\mathscr{M}}, c , w}\), this entails \(V_{{\mathscr{M}}, c, w^{*}}(\phi ) = 1\). Contradiction. Therefore, there is no model \({\mathscr{M}}\), no c ∈ C, no w ∈ W, and no \(\alpha \in A_{c} \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(\phi \wedge \Diamond \neg \phi ) = 1\). By (C1) it follows that ϕ ∧♢¬ϕ is e-weird.□
-
(L)
I am indebted to an anonymous reviewer for suggesting this strengthening of the theory.
If the negation is a wide scope negation [¬(The present king of France is bald)], then it will be true but if the negation has narrow scope [(The present king of France is ¬ bald], then it will be a presupposition failure which results neither in truth nor in falsity.
(R11) and (R12) can be directly proven by (C1) and (C1)*. I have provided the proof for (R13) above. The proof for (R14) is analogous since the order of the conjuncts does not matter in the semantics. (R15) and (R16) follow directly from (R13) by invoking the relevant projection rules (C3) and (C4). Only the proofs for (R17) and (R18) are harder. Let me briefly sketch the proof for (R17). The strategy for proving (R18) is similar:
Proof
To prove (R17) one first proves the following additional lemmas I will presuppose here:
-
(L1)
No atomic sentence p is e-weird
-
(L2)
No atomic sentence p is e-c-weird
-
(L3)
Kap is not e-c-weird
-
(L4)
¬Kap is not e-weird
-
(L5)
There is a model \({\mathscr{M}}\), a c ∈ C, a w ∈ W and a \(\alpha \in A_{c} \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(p \wedge \neg K_{a} p) = 1\)
All these lemmas require the construction of countermodels. (L2) is needed to prove (L3), which in turn is needed to prove (L4). The proof of (R17) from (L1), (L4), and (L5) is then straightforward: Assume for reductio that p ∧¬Kap is e-weird. This is either due to (C1) or due to (C2). If it is due to (C2), then either p is e-weird or ¬Kap is e-c-weird. But p is not e-weird by (L1) and ¬Kap is not e-weird by (L4). Thus, it is due to (C1) which means that there is no model \({\mathscr{M}}\), no c ∈ C, no w ∈ W and no \(\alpha \in A_{c} \cup {A_{c}^{i}}\) such that for all \(w^{\prime } \in S_{{\mathscr{M}}, c , w}(\alpha )\): \(V_{{\mathscr{M}}, c, w^{\prime }}(p \wedge \neg K_{a} p) = 1\). But this contradicts (L5). Therefore, p ∧¬Kap is not e-weird.□
-
(L1)
Thanks again to an anonymous reviewer for raising this doubt.
Some counterexamples might arise. If someone says ‘Let us assume that Anne is in New York. Then she must be in the US although we don’t know it. That’s crazy. She would have told us if she were in the US.’ In this case it is plausible that the speaker introduces a hypothetical agent (thereby changing the context) when she suggests to assume that Anne is in New York. She introduces a hypothetical agent who knows that Anne is in New York. This is what makes her must-claim true. But without evidence that someone makes an assumption like this we should treat every context as actual by default.
For instance, to answer a question from a reviewer, a claim like ‘Everyone knows that it is raining’ cannot be true in a context while ‘It must be raining’ is false in the very same context. ‘Everyone’ will range over the set of actual agents which is non-empty. Thus, there will be an actual agent who knows that it is raining. But then the fact that it is raining will be part of the combined knowledge in the context and ‘It must be raining’ will thus be true.
References
Beddor, B., & Goldstein, S. (2018). Believing epistemic contradictions. The Review of Symbolic Logic, 11(1), 87–114.
Bird, A., & Pettigrew, R. (2021). Internalism, externalism, and the KK principle. Erkenntnis, 86(6), 1713–1732.
Bledin, J. (2014). Logic informed. Mind, 123(490), 277–316.
Ciardelli, I. (2021). Restriction without quantification: Embedding and probability for indicative conditionals. Ergo, 8, 598–636.
Das, N., & Salow, B. (2018). Transparency and the KK principle. Noûs, 52(1), 3–23.
DeRose, K. (1991). Epistemic possibilities. The Philosophical Review, 100(4), 581–605.
Dorst, K. (2019). Abominable KK failures. Mind, 128(512), 1227–1259.
Egan, A., Hawthorne, J., & Weatherson, B. (2005). Epistemic modals in context. In G. Preyer G. Peter (Eds.) Contextualism in philosophy: knowledge, meaning and truth (pp. 131–170). Oxford: Oxford University Press.
Gauker, C. (2021). A strictly stronger relative must. Thought, 10 (2), 82–89.
Gillies, A. S. (2004). Epistemic conditionals and conditional epistemics. Nôus, 38(4), 585–616.
Goldstein, S. (2019). Generalized update semantics. Mind, 128 (511), 795–835.
Hawke, P., & Steinert-Threlkeld, S. (2021). Semantic expressivism for epistemic modals. Linguistics and Philosophy, 44, 475–511.
Incurvati, L., & Schlöder, J. J. (2019). Weak assertion. Philosophical Quaterly, 69(277), 741–770.
Kaplan, D. (1989). Demonstratives. In J. Perry H. Wett stein (Eds.) Themes from kaplan (pp. 481–563). Oxford: Oxford University Press.
MacFarlane, J. (2011). Epistemic modals are assessment sensitive. Epistemic modality (pp. 144–178). Oxford: Oxford University Press.
Mandelkern, M. (2019). Bounded modality. Philosophical Review, 122, 45–92.
Ninan, D. (2018). Relational semantics and domain semantics for epistemic modals. Journal of Philosophical Logic, 47(1), 1–16.
Punčochár, V., & Gauker, C. (2020). Indicative conditionals in objective contexts. Theoria, 86, 651–687.
Ramsey, F. P. (1931). General propositions and causality. In R.B. Braithwaite (Ed.) The foundations of mathematics and other logical essays (pp. 237–255). London: Kegan Paul, Trench, Trubner, & Co.
Ripley, D. (2013). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91(1), 139–164.
Russell, B. (1905). On denoting. Mind, 14(56), 479–493.
Stalnaker, R. C. (2015). Luminosity and the KK thesis. In S.C. Goldberg (Ed.) Externalism, self-knowledge, and skepticism (pp. 19–40). Cambridge: Cambridge University Press.
Teller, P. (1972). Epistemic possibility. Philosophia, 2, 303–320.
Unger, P. (1975). Ignorance: a case for scepticism. Oxford: Oxford University Press.
Willer, M. (2013). Dynamics of epistemic modality. Philosophical Review, 122(1), 44–92.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Williamson, T. (2020). Suppose and tell: the semantics and heuristics of conditionals. Oxford: Oxford University Press.
Yalcin, S. (2007). Epistemic modals. Mind, 116, 983–1026.
Acknowledgements
My special thanks go to Chris Gauker for invaluable support and comments during the time this paper was written. Secondly, I would like to thank an anonymous reviewer for astute comments and detailed suggestions, which lead to considerable improvement of this paper. Thanks also to Jack Spencer for some helpful discussion.
Funding
Open Access funding provided by the MIT Libraries.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The author declares no competing interests.
Additional information
Availability of Data and Material
Not applicable
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mayr, P. Epistemic Contradictions Do Not Threaten Classical Logic. Acta Anal 37, 551–573 (2022). https://doi.org/10.1007/s12136-021-00506-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12136-021-00506-9





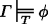 iff there is no model
iff there is no model