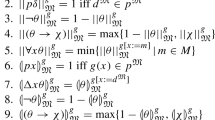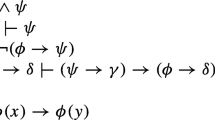Abstract
Interpretation is commonly used in mathematical logic to compare different theories and identify cases where two theories are for almost all intents and purposes the same. Similar techniques are used in the comparison between alternative logics although the links between these approaches are not transparent. This paper generalizes theoretical comparison techniques to the case of logical comparison using an extremely general approach to semantics that provides a very generous playing field upon which to make our comparisons. In particular, we aim to develop the useful idea that interpretations should determine inner models.
Similar content being viewed by others
Notes
For an excellent and thorough discussion of these techniques, see Visser (2004).
See French (2019) for a great overview of this.
That said formulae will always be represented by \(\varphi ,\psi\) and \(\chi\); never A, B, C. Given my goal is to bridge this work with that done in set theory and other areas of mathematical logic, more uniformity of notation seems desirable.
Note that on the left side of this identity we have an operator from the algebra, while on the right side we have the syntactic connective.
This makes our presentation simpler, however, we’ll show how to avoid this in Sect. 6.
Note that I am writing \(h``\Gamma\) to mean the pointwise image of \(\Gamma\) under h; i.e., \(h``\Gamma =\{h(\gamma )\ |\ \gamma \in \Gamma \}\).
This is called weak extensionality by Humberstone and is discussed on p. 455 of Humberstone (2011).
This is essentially Exercise 3.23.4 from Humberstone (2011). I should also note that we usually do not have a \(\top\) in strong Kleene. It makes no difference to the result above if we extend the language and its interpretation to accommodate \(\top\).
In some sense, providing a definition of logic could be construed as a challenge to find something that fails to satisfy it. Nonetheless, the definitions used in the paper provide a very broad umbrella.
Within the context of the proposed framework, I think it would be natural to regard Kripke’s semantics for S4 as being partially interpreted. By this we mean that there is structure in the Kripke semantics which is not determined by the consequence relation. For many applications, this structure is—of course—invaluable. Nonetheless, the underlying framework of this paper could be adapted to logics fitting the Kripke semantics provided there is a uniform means of defining the required semantics from the consequence relations of those logics.
We note that the converse does become available in stronger logics. For example, suppose that \({\mathcal {L}}\) contains a binary context (see Sect. 3.16 of Humberstone (2011) for a definition) \(\Sigma\) such that for all \(\Gamma \cup \{\varphi ,\psi \}\subseteq {\mathcal {L}}\), \(\Gamma \vdash \Sigma (\varphi ,\psi )\) iff \(\Gamma \cup \{\varphi \}\vdash \psi\) and \(\Gamma \cup \{\psi \}\vdash \varphi\). Then let \(\sim\) be an arbitrary consequence relation on \(\varvec{{\mathcal {L}}}\). We show there is some \(\Gamma\) such that \(\sim =\sim _{\Gamma }\). Let \(\Gamma =\{\Sigma (\varphi ,\psi )\ |\ \varphi \sim \psi \}\). Then we see that for all \(\varphi ,\psi \in \varvec{{\mathcal {L}}}\)
$$\begin{aligned} \varphi \sim \psi&\Leftrightarrow \Gamma \vdash \Sigma (\varphi ,\psi )\\&\Leftrightarrow \Gamma \cup \{\varphi \}\vdash \psi \ \& \ \Gamma \cup \{\psi \}\vdash \varphi \ \Leftrightarrow \ \varphi \sim _{\Gamma }\psi . \end{aligned}$$We remark more on this phenomenon in Sect. 6.1.
For a definition of context see Sect. 3.16 in Humberstone (2011). From the algebraic perspective, this is a term with a free variable.
The other operations are then defined by recursion.
This should be compared to condition (4) of Definition 17.
The intention here is that \(\#_{i}^{{\mathbb {A}}_{0}^{\dagger }}\) is the interpretation of the operator \(\#_{i}\) from \(\varvec{{\mathcal {L}}_{0}}\) in the model \({\mathbb {A}}_{0}^{\dagger }\).
Specifically, in the case of theories in classical first order logic, suppose we have a relative interpretation \(t:{\mathcal {L}}_{\in }\rightarrow {\mathcal {L}}_{\in }\) such that if \(S\vdash \varphi\), then \(T\vdash t(\varphi )\) for all \(\varphi \in {\mathcal {L}}_{\in }\). Then if \(t^{*}\) is the associated mod-functor, we know that for all models M satisfying T, we have
$$\begin{aligned} t^{*}(M)\models \varphi \ \Leftrightarrow \ M\models t(\varphi ). \end{aligned}$$See Remark 2.13.4 in Humberstone (2011) for references to a proof.
One might wonder if the algebraic semantics offered for algebraizable logics could be used to provide a further notion of interpretation. As far as I know, these semantics are less suitable for this purpose. This is because establishing that some logic is algebraizable in the sense of Blok and Pigozzi (1989) is often a non-trivial matter, while the semantics for a proto-algebraic logic just fall directly out of its consequence relation. I suspect this indicates that the algebraic semantics delivered for algebraizable logics is more informative that the semantics we have used above.
This approach is also adopted in Dewar (2018).
These are sometimes known as equivalential logics. See p. 267 of Pelletier and Urquhart (2003) for the axioms that must be satisfied. In particular, Kleene’s strong logic does not satisfy \(\vdash A\leftrightarrow A\).
This fits well with Woods’ goals since he is aiming to give a syntactic account. The account of this paper sits somewhere in between the syntactic and semantic realms.
This problem is easily surmountable. Moreover, Woods addresses it in an intriguing manner, which warrants further consideration. In particular, given logics \(\langle \varvec{{\mathcal {L}}},\vdash \rangle\) and \(\langle \varvec{{\mathcal {L}}}^{*},\vdash ^{*}\rangle\), Woods suggests that what we have called a relative interpretation should have two components \(t_{0},t_{1}:\varvec{{\mathcal {L}}}\rightarrow \varvec{{\mathcal {L}}}^{*}\) such that for all \(\Gamma \cup \{\varphi \}\in {\mathcal {L}}\), if \(\Gamma \vdash \varphi\), then \(t_{0}``\Gamma \vdash ^{*}t_{1}(\varphi ).\) Thus, we translate premises and conclusions of consequences differently. Woods argues that this extra dimension provides a better tool for respecting the intended meanings of the logics involved (Woods, 2018, p. 61).
I say surprising here to avoid obvious cases like the fact that intuitionistic logic is equivalent to classical logic if we include the law of excluded middle as an axiom schema.
References
Blok, W. J., & Pigozzi, D. (1986). Protoalgebraic logics. Studia Logica, 45(4), 337–369.
Blok, W. J., & Pigozzi, D. (1989). Algebraizable logics. American Mathematical Society.
Carnap, R. (1946). Modalities and quantification. Journal of Symbolic Logic, 11(2), 33–64.
Dewar, N. (2018). On translating between logics. Analysis, 78(4), 622–630.
French, R. (2019). Notational variance and its variants. Topoi, 40(38), 321–331.
French, R. (2011). Translational embeddings in modal logic. Ph.D. thesis, Monash University.
Humberstone, L. (2011). The connectives. MIT Press.
Jansana, R. (2016). Algebraic propositional logic. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
Kripke, S. (1963). Semantical considerations on modal logic. Acta Philosophica Fennica - Modal and Many-valued Logics, 16, 83–94.
McKinsey, J. C. C., & Tarski, Alfred. (1948). Some theorems about the sentential calculi of Lewis and Heyting. Journal of Symbolic Logic, 13(1), 1–15.
Meadows, T. (2015). Unpicking Priest’s bootstraps. Thought, 4(3), 181–188.
Meadows, T., & Weber, Z. (2016). Computation in non-classical foundations. Philosophers’ Imprint, 16(13), 1–17.
Pelletier, F. J., & Urquhart, A. (2003). Synonymous logics. Journal of Philosophical Logic, 32, 259–285.
Visser, A. (2004). Categories of theories and interpretations. Utrecht Logic Group Preprint Series, 26, 284–341.
Wigglesworth, J. (2017). Logical anti-exceptionalism and theoretical equivalence. Analysis, 77(4), 759–767.
Wigglesworth, J. (2019). Individuating logics: A category-theoretic approach. Thought: A Journal of Philosophy, 8(3), 200–208.
Woods, J. (2018). Intertranslatability, theoretical equivalence, and perversion. Thought: A Journal of Philosophy, 7(1), 58–68.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I would like to thank Rohan French, Tobi Koch and Kai Wehmeier for a number of stimulating conversations that inspired this paper and made it so much better. I would also like to thank the anonymous referees for their extremely helpful comments.
Rights and permissions
About this article
Cite this article
Meadows, T. Relative Interpretation Between Logics. Erkenn 88, 3203–3220 (2023). https://doi.org/10.1007/s10670-021-00498-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-021-00498-3