Skip to main content
SpringerLink
Log in

The Effect of Intrinsic and Acquired Resistances on Chemotherapy Effectiveness

  • Regular Article
  • Published:
Acta Biotheoretica Aims and scope Submit manuscript

Abstract

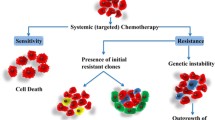
Although chemotherapy is one of the most common treatments for cancer, it can be only partially successful. Drug resistance is the main cause of the failure of chemotherapy. In this work, we present a mathematical model to study the impact of both intrinsic (preexisting) and acquired (induced by the drugs) resistances on chemotherapy effectiveness. Our simulations show that intrinsic resistance could be as dangerous as acquired resistance. In particular, our simulations suggest that tumors composed by even a small fraction of intrinsically resistant cells may lead to an unsuccessful therapy very quickly. Our results emphasize the importance of monitoring both intrinsic and acquired resistances during treatment in order to succeed and the importance of doing more experimental and genetic research in order to develop a pretreatment clinical test to avoid intrinsic resistance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Almendro V, Cheng YK, Randles A, Itzkovitz S, Marusyk A, Ametller E, Gonzalez-Farre X, Munoz M, Russnes HG, Helland A, Rye IH, Borresen-Dale AL, Maruyama R, van Oudenaarden A, Dowsett M, Jones RL, Reis-Filho J, Gascon P, Gonen M, Michor F, Polyak K (2014) Inference of tumor evolution during chemotherapy by computational modeling and in situ analysis of genetic and phenotypic cellular diversity. Cell Rep 6:514–527

    Article  Google Scholar 

  • Bertuzzi A, d’Onofrio A, Fasano A, Gandolfi A (2003) Regression and regrowth of tumour cords following single-dose anticancer treatment. Bull Math Biol 65:903–931

    Article  Google Scholar 

  • Casciari JJ, Sotirchos SV, Sutherland RM (1988) Glucose diffusivity in multicellular tumor spheroids. Cancer Res 48:3905–3909

    Google Scholar 

  • Chaplain M, Matzavinos A (2006) Mathematical modeling of spatio-temporal phenomena in tumor immunology. In: Friedman A (ed) Tutorials in mathematical biosciences III: cell cycle, proliferation, and cancer. Springer, New York, pp 131–183

  • Coldman AJ, Goldie JH (1985) Role of mathematical modeling in protocol formulation in cancer chemotherapy. Cancer Treat Rep 69:1041–1048

    Google Scholar 

  • de Pillis L, Fister KR, Gu W, Collins C, Daub M, Gross D, Moore J, Preskill B (2009) Mathematical model creation for cancer chemo-immunotherapy. Comput Math Methods Med 10:165–184

    Article  Google Scholar 

  • DeVita VT (1983) Progress in cancer management. Keynote address. Cancer 51:2401–2409

    Article  Google Scholar 

  • DeVita VT, Lawrence TS, Rosenberg SA, DePinho RA, Weinberg RA (2008) DeVita, Hellman, and Rosenberg’s cancer: principles and practice of oncology. Lippincott Williams & Wilkins, Philadelphia, USA

    Google Scholar 

  • d’Onofrio A, Gandolfi A (2010) Resistance to antitumor chemotherapy due to bounded-noise-induced transitions. Phys Rev E 82(061):901

    Google Scholar 

  • Drasdo D, Höhme S (2005) A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys Biol 2:133–147

    Article  Google Scholar 

  • Fang J, Sullivan M, McCutchan TF (2004) The effects of glucose concentration on the reciprocal regulation of rRNA promoters in plasmodium falciparum. J Biol Chem 279:720–725

    Article  Google Scholar 

  • Foo J, Michor F (2010) Evolution of resistance to anti-cancer therapy during general dosing schedules. J Theor Biol 263:179–188

    Article  Google Scholar 

  • Freyer JP, Sutherland RM (1985) A reduction in the in situ rates of oxygen and glucose consumption of cells in EMT6/Ro spheroids during growth. J Cell Physiol 124:516–524

    Article  Google Scholar 

  • Frieboes HB, Edgerton ME, Fruehauf JP, Rose FRAJ, Worrall LK, Gatenby RA, Ferrari M, Cristini V (2009) Prediction of drug response in breast cancer using integrative experimental/computational modeling. Cancer Res 69:4484–4492

    Article  Google Scholar 

  • Garner AL, Lau YY, Jackson TL, Uhler MD, Jordan DW, Gilgenbach RM (2005) Incorporating spatial dependence into a multicellular tumor spheroid growth model. J Appl Phys 98:1–8

    Article  Google Scholar 

  • Gerlinger M, Rowan AJ, Horswell S, Larkin J, Endesfelder D, Gronroos E, Martinez P, Matthews N, Stewart A, Tarpey P, Varela I, Phillimore B, Begum S, McDonald NQ, Butler A, Jones D, Raine K, Latimer C, Santos CR, Nohadani M, Eklund AC, Spencer-Dene B, Clark G, Pickering L, Stamp G, Gore M, Szallasi Z, Downward J, Futreal PA, Swanton C (2012) Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. New Engl J Med 366:883–892

    Article  Google Scholar 

  • Goldie JH, Coldman AJ (2009) Drug resistance in cancer: models and mechanisms. Cambridge University Press, Cambridge, UK

    Google Scholar 

  • Jackson TL (2003) Intracellular accumulation and mechanism of action of doxorubicin in a spatio-temporal tumor model. J Theor Biol 220:201–213

    Article  Google Scholar 

  • Jiang Y, Pjesivac-Grbovic J, Cantrell C, Freyer JP (2005) A multiscale model for avascular tumor growth. Biophys J 89:3884–3894

    Article  Google Scholar 

  • Johnstone RW, Ruefli AA, Lowe SW (2002) Apoptosis: a link between cancer genetics and chemotherapy. Cell 108:153–164

    Article  Google Scholar 

  • Kansal AR, Torquato S, Chiocca EA, Deisboeck TS (2000) Emergence of a subpopulation in a computational model of tumor growth. J Teor Biol 207:431–441

    Article  Google Scholar 

  • Kole AC, Plaat BEC, Hoekstra HJ, Vaalburg W, Molenaar WM (1999) FDG and L-[1-11C]-tyrosine imaging of soft-tissue tumors before and after therapy. J Nucl Med 40:381–386

    Google Scholar 

  • Lavi O, Gottesman MM, Levy D (2012) The dynamics of drug resistance: a mathematical perspective. Drug Resist Update 15:90–97

    Article  Google Scholar 

  • Lecca P, Morpurgo D (2012) Modelling non-homogeneous stochastic reaction–diffusion systems: the case study of gemcitabine-treated non-small cell lung cancer growth. BMC Bioinform. doi:10.1186/1471-2105-13-S14-S14

  • Lippert TH, Ruoff HJ, Volm M (2008) Resistance in malignant tumors: Can resistance assays optimize cytostatic chemotherapy? Pharmacology 81:196–203

    Article  Google Scholar 

  • Lippert TH, Ruoff H, Volm M (2011) Current status of methods to assess cancer drug resistance. Int J Med Sci 8:245–253

    Article  Google Scholar 

  • McKinnell RG, Parchment RE, Perantoni AO, Pierce GB, Damjanov I (2006) The biological basis of cancer. Cambridge University Press, New York, USA

    Book  Google Scholar 

  • Menchón SA, Condat CA (2008) Cancer growth: predictions of a realistic model. Phys Rev E 78:022901

    Article  Google Scholar 

  • Menchón SA, Condat CA (2009) Modeling tumor cell shedding. Eur Biophys J 38:479–485

    Article  Google Scholar 

  • Menchón SA, Condat CA (2011) Quiescent cells: a natural way to resist chemotherapy. Phys A 390:3354–3361

    Article  Google Scholar 

  • Murray JM, Coldman AJ (2003) The effect of heterogeneity on optimal regimens in cancer chemotherapy. Math Biosci 185:73–87

    Article  Google Scholar 

  • Norris ES, King JR, Byrne HM (2006) Modelling the response of spatially structured tumours to chemotherapy: drug kinetics. Math Comput Model 43:820–837

    Article  Google Scholar 

  • Panetta JC (1998) A mathematical model of drug resistance: heterogeneous tumors. Math Biosci 147:41–61

    Article  Google Scholar 

  • Priestman T (2008) Cancer chemotherapy in clinical practice. Springer-Verlag, London

    Google Scholar 

  • Raguz S, Yagüe E (2008) Resistance to chemotherapy: new treatments and novel insights into an old problem. Br J Cancer 99:387–391

    Article  Google Scholar 

  • Scalerandi M, Romano A, Pescarmona GP, Delsanto PP, Condat CA (1999) Nutrient competition as a determinant for cancer growth. Phys Rev E 59(2):2206–2217

    Article  Google Scholar 

  • Silva AS, Gatenby RA (2010) A theoretical quantitative model for evolution of cancer chemotherapy resistance. Biol Direct 5:25

    Article  Google Scholar 

  • Stein WD, Figg WD, Dahut W, Stein AD, Hoshen MB, Price D, Bates SE, Fojo T (2008) Tumor growth rates derived from data for patients in a clinical trial correlate strongly with patient survival: a novel strategy for evaluation of clinical trial data. Oncologist 13:1046–1054

    Article  Google Scholar 

  • Swan GW (1990) Role of optimal control theory in cancer chemotherapy. Math Biosci 101:237–284

    Article  Google Scholar 

  • Swanson KR, Bridge C, Murray JD, Alvord EC (2003) Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion. J Neurol Sci 216(1):1–10

    Article  Google Scholar 

  • Swierniak A, Kimmel M, Smieja J (2009) Mathematical modeling as a tool for planning anticancer therapy. Eur J Pharmacol 625:108–121

    Article  Google Scholar 

Download references

Acknowledgments

This work was partially supported by SeCyT-UNC (project 3072011-0100436) and CONICET (PIP 112-200801-00772) (Argentina). I would like to express my gratitude to Prof. Carlos Condat for his guidance, helpful advice and inspiring discussions.

Author information

Authors and Affiliations

  1. IFEG-CONICET and FaMAF, Universidad Nacional de Córdoba, Medina Allende s/n, Ciudad Universitaria, 5000, Córdoba, Argentina

    Silvia A. Menchón

Authors
  1. Silvia A. Menchón
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Silvia A. Menchón.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Menchón, S.A. The Effect of Intrinsic and Acquired Resistances on Chemotherapy Effectiveness. Acta Biotheor 63, 113–127 (2015). https://doi.org/10.1007/s10441-015-9248-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10441-015-9248-x

Keywords

Search

Navigation