Social Pressure from a Core Group can Cause Self-Sustained Oscillations in an Epidemic Model

Abstract

Let the individuals of a population be divided into two groups with different personal habits. The core group is associated with health risk behaviors; the non-core group avoids unhealthy activities. Assume that the infected individuals of the core group can spread a contagious disease to the whole population. Also, assume that cure does not confer immunity. Here, an epidemiological model written as a set of ordinary differential equations is proposed to investigate the infection propagation in this population. In the model, migrations between these two groups are allowed; however, the transitions from the non-core group into the core group prevail. These migrations can be either spontaneous or stimulated by social pressure. It is analytically shown that, in the scenario of spontaneous migration, the disease is either naturally eradicated or chronically persists at a constant level. In the scenario of stimulated migration, in addition to eradication and constant persistence, self-sustained oscillations in the number of sick individuals can also be found. These analytical results are illustrated by numerical simulations and discussed from a public health perspective.

Appendix

The type of Hopf bifurcation (supercritical, subcritical, or degenerate) can be determined by deriving the normal form of the underlying dynamical system, as summarized below (Guckenheimer and Holmes 2002).

Consider Eqs. (5)–(7) with $q=1$. First, shift the endemic equilibrium point to the origin of a new set of variables, by defining $X_1=S-S_{ende}^{1*}, X_2=S_c-S_{c,ende}^{1*}$, and $X_3=I_c-I_{c,ende}^{1*}$. In these new coordinates, Eqs. (5)-(7) are rewritten as $d\textbf{X}/{dt}=\textbf{f}(\textbf{X})$, with $\textbf{X}=(X_1,X_2,X_3)$ and $\textbf{f}=(f_1(\textbf{X}),f_2(\textbf{X}),f_3(\textbf{X}))$. Assume that the origin of this system experiences a Hopf bifurcation for a particular combination of parameter values. Thus, at this bifurcation point, the eigenvalues of the Jacobian matrix $\textbf{J}$ are $\lambda _{1,2}=\pm i \omega$ and $\lambda _3<0$. Let $\mathbf{v_1}=\textbf{a}+i\textbf{b}$ be an eigenvector associated with $\lambda _1=i\omega$ and $\mathbf{v_3}=\textbf{c}$ an eigenvector associated with $\lambda _3$. Let the columns of a matrix $\textbf{P}$ be formed by $\textbf{a}, -\textbf{b}$, and $\textbf{c}$. Then, rewrite $d\textbf{X}/{dt}=\textbf{f}(\textbf{X})$ in terms of $\textbf{Y}=(Y_1,Y_2,Y_3)$, so that $\textbf{Y}=\textbf{P}^{-1} \textbf{X}$. This new change of variables leads to:

$$\begin{aligned} \left[ \begin{array}{c} dY_1/dt \\ dY_2/dt \\ dY_3/dt \\ \end{array} \right] = \left[ \begin{array}{ccc} 0 &{} -\omega &{} 0 \\ \omega &{} 0 &{} 0 \\ 0 &{} 0 &{} \lambda _3 \\ \end{array} \right] \left[ \begin{array}{c} Y_1 \\ Y_2 \\ Y_3 \\ \end{array} \right] + \left[ \begin{array}{c} \psi (\textbf{Y}) \\ \varphi (\textbf{Y}) \\ \zeta (\textbf{Y}) \\ \end{array} \right] \end{aligned}$$

(A.1)

in which $\psi , \varphi$, and $\zeta$ are nonlinear functions of $\textbf{Y}$. Notice that the linear part of Eq. (A.1) is in the Jordan normal form (Guckenheimer and Holmes 2002). The matrix of this linear part is obtained from $\textbf{P}^{-1}{} \textbf{J}{} \textbf{P}$. The flow restricted to the center manifold near the origin can be described by $dY_1/dt$ and $dY_2/dt$, by taking (Guckenheimer and Holmes 2002):

$$\begin{aligned} Y_3=H(Y_1,Y_2)=k_1(Y_1)^2+k_2(Y_1Y_2)+k_3(Y_2)^2 \end{aligned}$$

(A.2)

Since $dY_3/dt = \lambda _3 Y_3 + \zeta$, then:

$$\begin{aligned} \frac{\partial H}{\partial Y_1} \frac{dY_1}{dt} + \frac{\partial H}{\partial Y_2} \frac{dY_2}{dt} - \lambda _3 H - \zeta = 0 \end{aligned}$$

(A.3)

or:

$$\begin{aligned} (2k_1 Y_1 + k_2 Y_2)(-\omega Y_2) + (k_2 Y_1 + 2k_3 Y_2) (\omega Y_1) - \lambda _3 H - \zeta \approx 0 \end{aligned}$$

(A.4)

The constants $k_1, k_2$, and $k_3$ in Eq. (A.2) are calculated by imposing that the coefficients of $(Y_1)^2, Y_1Y_2$, and $(Y_2)^2$ in Eq. (A.4) must be null (and neglecting the terms of higher orders). The first Lyapunov coefficient $L_1$, obtained from the functions $\psi (Y_1,Y_2,H(Y_1,Y_2))$ and $\varphi (Y_1,Y_2,H(Y_1,Y_2))$, is defined as Guckenheimer and Holmes (2002):

$$\begin{aligned} L_1= & {} \frac{1}{16}\left[ \psi _{Y_1 Y_1 Y_1} + \psi _{Y_1 Y_2 Y_2} + \varphi _{Y_1 Y_1 Y_2} + \varphi _{Y_2 Y_2 Y_2} \right] + \nonumber \\{} & {} \frac{1}{16\omega } \left[ \psi _{Y_1 Y_2} (\psi _{Y_1 Y_1} + \psi _{Y_2 Y_2})\right. \nonumber \\{} & {} \quad \left. - \varphi _{Y_1 Y_2} (\varphi _{Y_1 Y_1} + \varphi _{Y_2 Y_2}) - \psi _{Y_1 Y_1} \varphi _{Y_1 Y_1}+\psi _{Y_2 Y_2} \varphi _{Y_2 Y_2} \right] \end{aligned}$$

(A.5)

in which $\psi _{Y_1 Y_1 Y_1} = \partial ^3 \psi / \partial Y_1^3, \psi _{Y_1 Y_2 Y_2} = \partial ^3 \psi / \partial Y_1 \partial Y_2^2$ and so on. The coefficient $L_1$ must be computed at the bifurcation point. If $L_1<0$, the Hopf bifurcation is supercritical and the emerging limit cycle is asymptotically stable; if $L_1>0$, the Hopf bifurcation is subcritical and the emerging limit cycle is unstable (Guckenheimer and Holmes 2002).

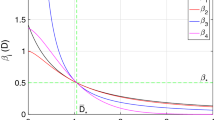
For the proposed model, Eqs. (5)–(7) can be rewritten as explained above from the following matrix $\textbf{P}$:

$$\begin{aligned} \textbf{P} \; = \; \left[ \begin{array}{ccc} 0 &{} \dfrac{-(w^2+EF)}{DF} &{} \dfrac{A^2-EF}{DF} \\ \dfrac{\omega }{F} &{} 0 &{} \dfrac{A}{F} \\ 0 &{} 1 &{} 1 \\ \end{array} \right] \end{aligned}$$

(A.6)

in which $A=-\delta _1^1=\lambda _3, D=\epsilon S_c^{1*}, E=-\alpha S_c^{1*}, F=\alpha I_c^{1*}$, and $\omega = \sqrt{\delta _2^1}$. The matrix inverse $\textbf{P}^{-1}$ is given by:

$$\begin{aligned} \textbf{P}^{-1} \; = \; \left[ \begin{array}{ccc} \dfrac{-ADF}{\omega (\omega ^2+A^2)} &{} \dfrac{F}{\omega } &{} \dfrac{-A(\omega ^2+EF)}{\omega (\omega ^2+A^2)} \\ \dfrac{-DF}{\omega ^2+A^2} &{} 0 &{} \dfrac{A^2-EF}{\omega ^2+A^2} \\ \dfrac{DF}{\omega ^2+A^2} &{} 0 &{} \dfrac{\omega ^2+EF}{\omega ^2+A^2} \\ \end{array} \right] \end{aligned}$$

(A.7)

Let $p_{ij}$ be the coefficient (i, j) of $\textbf{P}$ and $\eta _{ij}$ the coefficient (i, j) of $\textbf{P}^{-1}$. For the proposed model:

$$\begin{aligned} k_1= & {} \frac{\omega k_2}{A} \end{aligned}$$

(A.8)

$$\begin{aligned} k_2= & {} \frac{A p_{21}(\epsilon p_{12} \eta _{31} - \alpha \eta _{33}) + 2 a \omega p_{12} \eta _{31} }{4 \omega ^2+A^2} \end{aligned}$$

(A.9)

$$\begin{aligned} k_3= & {} \frac{a p_{12} \eta _{31} - \omega k_2 }{A} \end{aligned}$$

(A.10)

As a consequence:

$$\begin{aligned} \psi _{Y_1 Y_1}= & {} 0 \end{aligned}$$

(A.11)

$$\begin{aligned} \psi _{Y_1 Y_2}= & {} \epsilon p_{12} (1- p_{21} \eta _{11}) + \alpha (p_{21} \eta _{13}-1) \end{aligned}$$

(A.12)

$$\begin{aligned} \psi _{Y_2 Y_2}= & {} - 2a p_{12} \eta _{11} \end{aligned}$$

(A.13)

$$\begin{aligned} \psi _{Y_1 Y_1 Y_1}= & {} 6(- \epsilon p_{13} p_{21} k_1 \eta _{11} + (\epsilon p_{13} - \alpha )k_1 + \alpha k_1 p_{21} \eta _{13}) \end{aligned}$$

(A.14)

$$\begin{aligned} \psi _{Y_1 Y_2 Y_2}= & {} 2(-(\epsilon (p_{12} p_{23} k_2 + p_{13} p_{21}k_3) -a k_2 (p_{12}+p_{13}))\eta _{11} \nonumber \\{} & {} + (\epsilon (p_{12}p_{23}k_2+p_{21}k_3) - \alpha (p_{21}k_3+p_{23}k_2))\eta _{12} \nonumber \\{} & {} + \alpha (p_{21}k_3 + p_{23}k_2)\eta _{13}) \end{aligned}$$

(A.15)

$$\begin{aligned} \varphi _{Y_1 Y_1}= & {} 0 \end{aligned}$$

(A.16)

$$\begin{aligned} \varphi _{Y_1 Y_2}= & {} -\epsilon p_{12} p_{21} \eta _{21} + \alpha p_{21} \eta _{23} \end{aligned}$$

(A.17)

$$\begin{aligned} \varphi _{Y_2 Y_2}= & {} - 2a p_{12} \eta _{21} \end{aligned}$$

(A.18)

$$\begin{aligned} \varphi _{Y_2 Y_2 Y_ 2}= & {} 6(-(\epsilon p_{12}p_{23}+ap_{12}+ap_{13})k_3 \eta _{21} + \alpha p_{23} k_3 \eta _{23}) \end{aligned}$$

(A.19)

$$\begin{aligned} \varphi _{Y_1 Y_1 Y_2}= & {} 2(-(\epsilon (p_{12}p_{23}k_1+p_{13}p_{21}k_2)+a k_1(p_{12}+p_{13}))\eta _{21} \nonumber \\= & {} + \alpha (p_{21}k_2 + p_{23}k_1)\eta _{23}) \end{aligned}$$

(A.20)

The coefficient $L_1$ is computed from Eqs. (A.11)–(A.20).

Fig. 1

Time evolutions of S(t) (blue line), $S_c(t)$ (green line), I(t) (red line), and $I_c(t)$ (magenta line) for $q=0, b=0.05, c=0.02, \beta =0.04, \gamma =0.03, \epsilon =0.025, m=0.02$, and $N=1$ from the initial condition $(S(0),S_c(0),I(0),I_c(0))=(0.97,0.01,0.01,0.01)$. In (a), $a=1/20$ and $\alpha =1/10$. In this case, $(S(t),S_c(t),I(t),I_c(t)) \rightarrow (S^{0*}_{free}, S_{c,free}^{0*}, I_{free}^{0*}, I_{c,free}^{0*}) = (0.444, 0.556, 0, 0)$. In (b), $a=2/5$ and $\alpha =4/5$. In this case, $(S(t),S_c(t),I(t),I_c(t)) \rightarrow (S^{0*}_{ende}, S_{c,ende}^{0*}, I_{ende}^{0*}, I_{c,ende}^{0*}) = (0.442, 0.088, 0.337, 0.133)$

Fig. 2

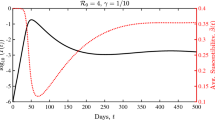
Time evolutions of S(t) (blue line), $S_c(t)$ (green line), I(t) (red line), and $I_c(t)$ (magenta line) for $q=1, b=0.05, c=0.02, \beta =0.04, \gamma =0.03, \epsilon =0.025$, and $N=1$ from the initial condition $(S(0),S_c(0),I(0),I_c(0))=(0.97,0.01,0.01,0.01)$. In (a), $a=1/6, \alpha =1/3$, and $m=0.03$. In this case, $(S(t),S_c(t),I(t),I_c(t)) \rightarrow (S^{1*}_{clean}, S_{c,clean}^{1*}, I_{clean}^{1*}, I_{c,clean}^{1*}) = (1, 0, 0, 0)$. In (b), $a=1/6, \alpha =1/3$, and $m=0.02$. In this case, $(S(t),S_c(t),I(t),I_c(t)) \rightarrow (S^{1*}_{free}, S_{c,free}^{1*}, I_{free}^{1*}, I_{c,free}^{1*}) = (0.8, 0.2, 0, 0)$. In (c), $a=2/5, \alpha =4/5$, and $m=0.02$. In this case, $(S(t),S_c(t),I(t),I_c(t)) \rightarrow (S^{1*}_{ende}, S_{c,ende}^{1*}, I_{ende}^{1*}, I_{c,ende}^{1*}) = (0.894, 0.088, 0.015, 0.003)$. In (d), $a=2, \alpha =4$, and $m=0.02$. In this case, $(S(t),S_c(t),I(t),I_c(t))$ converge to a self-sustained oscillation