Skip to main content
SpringerLink
Log in

Completeness and Doxastic Plurality for Topological Operators of Knowledge and Belief

  • Original Research
  • Published:
Erkenntnis Aims and scope Submit manuscript

Abstract

The first aim of this paper is to prove a topological completeness theorem for a weak version of Stalnaker’s logic KB of knowledge and belief. The weak version of KB is characterized by the assumption that the axioms and rules of KB have to be satisfied with the exception of the axiom (NI) of negative introspection. The proof of a topological completeness theorem for weak KB is based on the fact that nuclei (as defined in the framework of point-free topology) give rise to a profusion of topological belief operators that are compatible with the familiar topological knowledge operator Int. Thereby a canonical topological model for weak KB can be constructed. For this canonical model a truth lemma for the modal operators K and B holds such that a completeness theorem for weak KB can be proved in the familiar way. The second aim of this paper is to show that the topological interpretation of knowledge Int comes along with a complete Heyting algebra of belief operators N° that all fit the knowledge operator Int in the sense that the pairs (Int, N°) satisfy all axioms of weak KB. This amounts to a pluralistic relation between knowledge and belief: Knowledge does not fully determine belief, rather it designs a conceptual space for belief operators where different (competing) belief operators coexist that can be compared with each other.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. In topological terms Stalnaker’s operator NS is defined as the concatenation IntClInt, where, as usual, the interior kernel operator of a topological space (X, OX) is denoted by Int and the topological closure is denoted by Cl. In this paper this (more or less standard) topological terminology is used throughout. In more detail it is explained in Sect. 3.

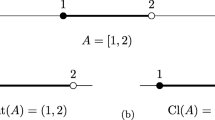
  2. For a more detailed presentation of LK, the reader may consult the recent papers of Baltag et al., (2017, 2019) and Aiello et al. (2003)).

  3. The topological terminology used in this paper is standard. Nevertheless, for the sake of definiteness, the topological concepts to be used will be explained in full detail in Sects. 3 and 4.

  4. The topological reason for the failure of (NI) in general spaces may be informally described as the fact that (NI) requires that many clopen (= open and closed) subsets exist. General topological spaces, however, may lack sufficiently many clopen sets. For instance, connected spaces such as the Euclidean line (ℝ, Oℝ) have only Ø and ℝ as clopen subsets.

  5. That is, the elegant equivalence of Stalnaker (2006) and Baltag et al. (2019) that B \(\neg\) K \(\neg\) K is no longer valid. In contrast, weak KB turns out to be a truly bimodal extension of CL, i.e., B cannot uniquely be defined in terms of K.

  6. For various equivalent definitions of a normal modal logic, see Chellas (1980, Theorem 4.3, p. 115).

  7. Elementary examples based on the Euclidean line (ℝ, Oℝ) show that there are models of weak KB logic the B-fragment of which are not KD45 models (cf. Proposition (4.11)).

  8. The necessity of introducing nuclei for defining the semantics of belief operators distinguishes weak KB logic from original KB logic. Since for KB systems the belief modality B can be defined in terms of K, in these systems the excursion into the theory of nuclei can be avoided, since the semantics of B can be defined in terms of the semantics of K. This is not the case for weak KB. Then, the modal operator B need not be definable in terms of K.

  9. The literature on nuclei in point-free topology has reached a high level of technical sophistication. This paper does not aim to give a full-fledged introduction into the theory of nuclei. Instead, we intend to provide the basic definitions and facts so that the reader can understand that this theory has interesting applications regarding the modal theory of belief and knowledge. For a fuller account, the reader may consult Johnstone (1982), Borceux (1994), or Picado and Pultr (2012, 2021) and the extensive bibliographies on point-free topology mentioned there.

  10. The reader should not be confused by this (established) terminology: every open subset A of X (as an element of OX) defines a closed nucleus and an open nucleus, namely, kA and jA, respectively.

  11. In this paper the regular nucleus IntCl is also called the Stalnaker nucleus and denoted by NS, since it has played such a prominent role in the topological interpretation of Stalnaker’s logic KB, cf. Baltag et al. (20172019)

  12. Clearly, a nucleus N and its corresponding belief operator N° determine each other uniquely: N = iN°Int and N° = IntNi. Here, i is, of course, the canonical inclusion i: OX→PX

  13. Sublocales are also called ⇒-ideals.

  14. Actually there is an order-reversing bijection between nuclei and sublocales: A nucleus N:OXOX is uniquely determined by its image i:N(OX)OX. Indeed, N(OX) OX is a sublocale. Thus, a nucleus uniquely determines a sublocale. On the other hand, the inclusion map of a sublocale i:SOX has an adjoint frame map j:OXS such that the concatenation ij:OXOX is a nucleus N [cf. Johnstone (2002, Proposition 1.1.3., p. 486), Picado and Pultr (2012, 5.3.2. Proposition. p. 32)]. We don’t need this result, however.

  15. According to Aiello et al., (2003, p. 896) the canonical topology of the canonical space is the intersection of the Kripke topology and the Stone topology. This entails that this space is compact and dense-in-itself.

  16. If the axiom (NI) of negative introspection is assumed to be valid, the bimodal logic KB boils down to a unimodal logic defined by K since then the belief modality B can be uniquely defined in terms of K, namely B = \(\neg\) K \(\neg\) K (cf. Footnote 4).

  17. This section is somewhat technical. Readers who believe that a knowledge operator Int is always accompanied by many belief operators may therefore skip this section on first reading.

  18. TD is a rather weak axiom satisfied by most topological spaces that “occur in nature”. For instance, Euclidean spaces and, more generally, all T2-spaces, and all T0-Alexandroff spaces are TD-spaces.

  19. Already in Macnab (1981) it is proved that for TD -spaces (X, OX) there is a Boolean isomorphism between PX and the Boolean algebra of regular elements of NUC(OX) [cf. Macnab (1981, Theorem (6.5)(5)]. In contrast, even for the Euclidean line (ℝ, Oℝ) the full structure of NUC(Oℝ) is not fully known up to now (as far as I know).

  20. Roughly, the relation between dense subspaces and dense nuclei of a topological space (X, OX) may be compared with the relation between the field of rational numbers ℚ and the field of complex numbers \(\mathbb{C}\) with respect to their algebraic qualities. A very simple aspect of this issue concerns the solvability of polynomial equations. While there are enough complex numbers to solve all polynomial equations in a neat and elegant way, this does not hold for the more restricted domain of rational numbers ℚ. It is quite difficult to say anything general about the solvability of polynomial equations in rational numbers.

  21. With some more effort it can be easily shown that there exist many spatial nuclei N1, N2 in NUC(Oℝ)d such that N1\(\vee\)N2 is non-spatial and different from NS = IntCl.

  22. Rumfitt’s polar spaces have been well known in topology. They may be characterized as submaximal Alexandroff spaces (cf. Bezhanishvili et al., 2014; Mormann, 2022).

  23. Zarycki (1930) erroneously claimed that PF is distributive with respect to \(\cup\) for all subsets A, D of X, not only for closed ones. This error was observed by Vaidyanathaswamy (1947) and Oxtoby (1976). Oxtoby proved a more complex formula for all subsets A, D that yields (6.12)(iv) for closed sets. For our purposes it is sufficient that distributivity ((6.14)(iv)) holds for closed subsets of X.

    Simmons (1978, 1982) stated (without explicit proof) that (6.14) (iv) holds, i.e., that the operation PF is distributive with respect to \(\cup\) for closed sets. He then went on to show that PF(AC)C is a nucleus. Actually, Oxtoby proved his more general results on PF only for T1-spaces. A closer inspection of his proof, however, reveals that for the distributivity of PF his proof works for all topological spaces.

  24. A Polish space is a separable topological space that is homeomorphic to a complete metric space [cf. Jech (2002, Definition (4.12), p. 44)].

  25. Already Stalnaker (2006) pointed out that on general topological spaces the operator ClInt does not define a (reasonable) belief operator, since it is not a normal operator, i.e., does not satisfy (2.6)(i) [cf. Stalnaker (2006, p. 195)]. An example for this fact is already provided by the Euclidean line (ℝ, Oℝ).

  26. DSO is an acronym for “Derived Sets are Open.”

References

  • Aiello, M., van Benthem, J. F. A. K., & Bezhanishvili, G. (2003). Reasoning about space: The modal way. Journal of Logic and Computation, 13(6), 889–920.

    Article  Google Scholar 

  • Aull, C. E., & Thron, W. J. (1963). Separation axioms between T0 and T1. Indagationes Mathematicae, 24, 26–37.

    Google Scholar 

  • Baltag, A., Bezhanishvili, N., Özgün, A., & Smets, S. (2017). The topology of full and weak Belief. In H. H. Hansen, S. E. Murray, M. Sadrzadeh, & H. Zeevat (Eds.), Logic, language, and computation (pp. 205–228). Springer.

    Chapter  Google Scholar 

  • Baltag, A., Bezhanishvili, N., Özgün, A., & Smets, S. (2019). A topological approach to full belief. Journal of Philosophical Logic, 48, 205–244.

    Article  Google Scholar 

  • Bezhanishvili, N., & van der Hoek, W. (2014). Structures for epistemic logic. In A. Baltag & S. Smets (Eds.), Johan van Benthem on logic and information dynamics (pp. 381–404). Springer.

    Google Scholar 

  • Blackburn, P., de Rijke, M., & Venema, Y. (2010). Modal logic, 4th printing. Cambridge University Press.

    Google Scholar 

  • Borceux, F. (1994). Handbook of categorical algebra 3. Cambridge University Press.

    Book  Google Scholar 

  • Chellas, B. F. (1980). Modal logic. Cambridge University Press.

    Book  Google Scholar 

  • Jech, T. (2002). Set theory, 3rd millenium edition, revised and expanded. Heidelberg.

    Google Scholar 

  • Johnstone, P. (1982). Stone spaces. Cambridge University Press.

    Google Scholar 

  • Johnstone, P. (1991). The art of pointless thinking: a student’s guide to the category of locales. In H. Herrlich & H. E. Porst (Eds.), Category Theory at Work Research and Exposition in Mathematics (pp. 85–107). Heldermann Verlag.

    Google Scholar 

  • Johnstone, P. (2002). Sketches of an elephant: a topos theory compendium. Clarendon Press.

    Google Scholar 

  • Kuratowski, K. (1966). Topology I. Academic Press, New York.

  • Macnab, D. S. (1981). modal operators on heyting algebras. Algebra Universalis, 12, 5–29.

    Article  Google Scholar 

  • Mormann, T. (2021). Prototypes, poles, and topological tessellations of conceptual spaces. Synthese, 199, 3675–3710.

    Article  Google Scholar 

  • Mormann, T. (2022). Topological models of columnar vagueness. Erkenntnis, 87(2), 693–716.

    Article  Google Scholar 

  • Oxtoby, J. F. (1976). The kernel Operation on subsets of a T1-space, Fundamenta Mathematicae 90(3), 275–284.

  • Parikh, R., Moss, S, Steinsvold, C. (2007). Topology and epistemic logic. In Handbook of Spatial Logic, 299–341.

  • Picado, J., Pultr, A. (2012). Frames and locales, topology without points, Basel, Birkhäuser.

  • Picado, J., & Pultr, A. (2021). Separation in point-free topology. Springer.

    Book  Google Scholar 

  • Rumfitt, I. (2015). The boundary stones of thought: an essay in the philosophy of logic. Oxford University Press.

    Book  Google Scholar 

  • Simmons, H. (1978). A framework for topology. In Logic Colloquium ’77, Studies in Logic foundations Math. Vol. 96, (pp. 239–251). Amsterdam, New York.

  • Simmons, H. (1980). Spaces with Boolean ASSEMBLIES. Colloquium Mathematicum, 43, 23–39.

    Article  Google Scholar 

  • Simmons, H. (1982). An algebraic version of Cantor-Bendixson analysis. In: Lecture notes in Mathematics. (pp. 310–323). Springer, Berlin.

  • Steinsvold, C. (2006). Topological models of belief, PhD Thesis, CUNY, Graduate Center.

  • Stalnaker, R. (2006). On logics of knowledge and belief. Philosophical Studies, 128, 169–199.

    Article  Google Scholar 

  • Steen, L. A., & Seebach, J. A., Jr. (1978). Counterexamples in topology. Springer.

    Book  Google Scholar 

  • Steen, L. A., Seebach Jr., & J. A. (1982). Counter examples in Topology. Second edition, New York, Heidelberg, Berlin, Springer.

  • Vaidyanathaswamy, R. (1947). Treatise on Set Topology I. Indian Mathematical Society, Madras

  • Van Benthem, J., & Bezhanishvili, G. (2007). Modal logics of space. Handbook of spatial logics (pp. 217–298). Springer.

    Chapter  Google Scholar 

  • Willard, St. (2004). General topology. Dover Publications.

    Google Scholar 

  • Zarycki, M. (1930). Über den Kern einer Menge, Jahresbericht der Deutschen Mathematiker-Vereinigung 39, 154–158.

Download references

Acknowledgments

I’d like to thank two anonymous referees for extremely useful critical comments that helped me to improve earlier versions of this paper considerably. Of course, I am solely responsible for all remaining shortcomings and deficits the article. Further, I should like to express my sincere gratitude to Nasim Mahoozi for general advice, conversations and support when writing this paper.

Author information

Authors and Affiliations

  1. Tsukuba, Japan

    Thomas Mormann

Authors
  1. Thomas Mormann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thomas Mormann.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mormann, T. Completeness and Doxastic Plurality for Topological Operators of Knowledge and Belief. Erkenn (2023). https://doi.org/10.1007/s10670-023-00666-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10670-023-00666-7

Search

Navigation