Truthlikeness: old and new debates

Abstract

The notion of truthlikeness or verisimilitude has been a topic of intensive discussion ever since the definition proposed by Karl Popper was refuted in 1974. This paper gives an analysis of old and new debates about this notion. There is a fairly large agreement about the truthlikeness ordering of conjunctive theories, but the main rival approaches differ especially about false disjunctive theories. Continuing the debate between Niiniluoto’s min-sum measure and Schurz’s relevant consequence measure, the paper also gives a critical assessment of Oddie’s new defense of the average measure and Kuipers’ refined definition of truth approximation.

1 Prologue: meeting with Gerhard Schurz

I met Gerhard Schurz for the first time in July 1983 in Salzburg, where he worked as a post doc with Professor Paul Weingartner. I had studied the notion of truthlikeness since 1975 (see Niiniluoto 1977), and presented an invited paper of truth approximation and idealized theories in the Seventh International Congress of Logic, Methodology and Philosophy of Science, locally chaired by Weingartner in Salzburg.

My next meeting with Gerhard was in August 1986 in Kirchberg at the Eleventh Wittgenstein Symposium. While I was talking about realism and scientific progress, he presented a paper “A New Definition of Verisimilitude and Applications”. Its basic idea was to rescue Karl Popper’s comparative definition of verisimilitude, which had been refuted by Miller (1974) and Tichý (1974), by restricting the truth and falsity contents of a theory to its relevant consequences. I immediately raised an objection to Theorem 5.3 of his hand-written handout: for false theories which have no true relevant consequences verisimilitude decreases with increasing logical strength. In a letter on September 30, 1986, I stated a counterexample:

Let p say that the number of moons in our solar system is 2, and q say that it is 2 or 2000. Then the stronger falsity p is closer to the truth than the weaker q.¹

I added that examples of this sort seem to prove that a satisfactory general definition of verisimilitude cannot be given merely by the concepts of truth value and deduction (whatever restrictions are given to the latter notion), but we need also a concept of distance or similarity.

Schurz sent his reply in a letter on October 3, 1986. He agreed with the judgment of my example, but pointed out that it presupposes that one can compare p and q for their verisimilitude, whereas his theorem 5.3 concerns qualitative cases without any “internal metric” for primitive predicates or propositions. For such situations the only plausible way of comparison is based on logical strength: the stronger falsity has less verisimilitude. Schurz assured further that he was looking for a natural embedding of a distance measure for “internally ordered” primitives into the relevant consequence approach. But this was not yet developed in the soon published joint paper of Schurz and Weingartner (1987).

One had to wait for the publication of Schurz and Weingartner (2010) to see how they propose to integrate a quantitative weight function into the relevant consequence approach. But, alas, the same theorem is still valid: among “completely false theories” (with empty restricted truth content) truthlikeness decreases with logical strength. Thus, the old debate, which started some 30 years ago, is still among us.

We shall return to the issue about false disjunctions in Sect. 5 after reviewing several other approaches and disputes about them. Section 2 summarizes some attempts to rescue Popper’s original definition. Section 3 outlines the similarity approach and the controversy between Oddie’s (1986) average measure and Niiniluoto’s (1987) min-sum-measure. Section 4 shows that there is in fact quite a lot of convergence between rival approaches, if one restricts attention to conjunctive theories. Finally, Sect. 5 illustrates different intuitions about verisimilitude by showing how the main rival accounts give different answers to the ordering of false disjunctions.

2 Reactions to Popper’s retreat

In 1960 Karl Popper gave a comparative definition for one scientific theory to be closer to the truth than another rival theory. His notion of verisimilitude or truthlikeness was intended to express the idea of “a degree of better (or worse) correspondence to truth” or of “approaching comprehensive truth” (see Popper 1963). For Popper, in his debate with Thomas Kuhn, it was also crucially important that this notion gives a definition of scientific progress as increasing verisimilitude.

Let T be the class of true statements and F the class of false statement in a given interpreted scientific language L. Let A and B be consistent theories, i.e. deductively closed classes of statements in L. Popper suggested that theory B is at least as truthlike as theory A if and only if

• (1) A ∩ T ⊆ B ∩ T and B ∩ F ⊆ A ∩ F.

Here A ∩ T is the truth content of A, and A ∩ F is the falsity content of A. B is more truthlike than A if at least one of the inclusions in (1) is strict. This is the case when the symmetric difference B Δ T = (B–T) ∪ (T–B) is a proper subset of A Δ T.

Popper’s definition has some nice properties:

• (TR1) T is more truthlike than any other theory A.

• (TR2) If A and B are true, and B entails A, but not vice versa, then B is more truthlike than A.

• (TR2a) If A and B are true, and B entails A, then B is at least as truthlike as A.

• (TR3) If A is false, then A ∩ T is more truthlike than A.

Here TR1 says that the whole truth T is maximally truthlike. According to TR2, among true theories, truthlikeness covaries with logical strength. TR2a is a weaker version of TR2. TR3 says that the truth content of a false theory is more truthlike than the theory itself.

Many theories are incomparable by (1). In particular, Popper’s definition does not allow that a false statement is so close to the truth that it is cognitively better than ignorance, where ignorance is represented by a tautology, i.e. the weakest true theory in L. Thus, the following principle is not satisfied:

• (TR4) Some false theories may be more truthlike than some true theories.

To illustrate TR4, for the cognitive problem about the number of planets (i.e. 8), the approximately true answer “9” is more truthlike than the tautological answer “any number greater than or equal to 0” or “I don’t know”. It is even better than its true negation “different from 9”.

Miller (1974) and Tichý (1974) proved that Popper’s definition does not work in the intended way, since it cannot be used for comparing false theories: if A is more truthlike than B in Popper’s sense, then A must be true. Thus, the following non-triviality principle is violated:

• (TR5) A false theory may be more truthlike than another false theory.

Both conditions TR4 and TR5 are important, if the notion of truthlikeness is to yield the hoped-for criterion of scientific progress, since for a fallibilist science typically develops by the replacement of a false theory by a better false theory, while the accumulation of truths in the sense of TR2 is only a rare special case.²

Popper’s first public reaction to Miller’s result was to restrict comparisons of theories to their truth content, but this leads to the fatal “child’s play objection” by Tichý (1974): any false theory can be improved by adding arbitrary falsities to it. In his Introduction to the volume of Postscript to the Logic of Scientific Discovery, Popper claimed that the admitted failure of his definition of verisimilitude has only negligible impact on his theory of science (see Popper 1982, pp. xxxv–xxxvii). A formal definition of verisimilitude is “not needed for talking sensibly about it”. A new definition is needed only if it strengthens a theory, and it is “completely baseless” to claim that this unfortunate mistaken definition weakens his theory. Popper added that no one has ever shown “why the idea of verisimilitude (which is not an essential part of my theory) should not be used further within my theory as an undefined concept”.

After this dramatic retreat by Popper, some of his followers suggested that critical rationalists need no precise notion of truthlikeness (John Watkins, Noretta Koertge, Hans Albert). Miller (1994) has continued to endorse Popperian falsificationism, even though he is skeptical of the possibility of finding a language-invariant definition of verisimilitude.³ Still, many philosophers advocating scientific realism made efforts to rescue Popper’s definition by logical means (cf. Niiniluoto 2017).

A model-theoretic version of Popper’s approach has been proposed by Miller (1978) and Kuipers (1982). Let Mod(A) be the class of models of A, i.e. the L-structures in which all the sentences of A are true. Then define A to be at least as truthlike as B if and only if

• (3) Mod(A) Δ Mod(T) ⊆ Mod(B) Δ Mod(T).

But if T is a complete theory, then this model-theoretic definition has an implausible consequence: among false theories, if theory B is logically stronger than A, then B is also more truthlike than A. Definition (3) is thus vulnerable to Tichý’s “child’s play objection”, and the following adequacy condition is not satisfied:

• (TR6) Among false theories, truthlikeness does not always increase with logical strength.

Miller’s later attempts to characterize truthlikeness by objective metrics have also led to violations of the principle TR6 (see Miller 1994, pp. 205, 215). To illustrate the problem with TR6, the stronger falsity “more than 100” is not better than the weaker falsity “9 or more than 100” for the question about the true number of planets. But for the same reason, we should disagree with Laymon’s (1987) conclusion that the weaker of two false theories is always more truthlike, i.e. we require

• (TR7) Among false theories, truthlikeness does not always decrease with logical strength.

For example, the weaker claim “9 or more than 100” is not better than “9” as an estimate of the number of planets (see Niiniluoto 1998).⁴

Several other logical treatments of verisimilitude violate the conditions TR4 or TR6. For example, the treatment by means of deductive power relations by Brink and Heidema (1987) disagrees with TR4. Mormann (2006) applies sophisticated mathematical tools of topology and metric spaces to the logical space of theories, which is “naturally ordered with respect to logical strength”, and derives from these considerations the definition (3) and, as its improvement, a metric which preserves the order (3) “as far as possible”.

Kuipers (1982) applies the definition (3) to what he calls “nomic truthlikeness”: a theory A asserts the physical possibility of the structures in Mod(A),⁵ claiming that Mod(A) is identical with the class Mod(T) of all physically possible structures or “nomic possibilities”. In this context T is usually not a complete theory.⁶ Kuipers (1987b) argues that Popper had “bad luck” when he formulated his intuition with statements [see (1)] instead possibilities, since (3) can be read so that all rightly admitted possibilities by B are admitted by A and all wrongly admitted possibilities of A are admitted by B. While this treatment avoids the Miller–Tichý trivialization and satisfies TR5, it violates TR4. Kuipers admits that the “naive definition” (3) is simplified in the sense that it treats all mistaken applications of a theory as equally bad. For this reason, and to avoid the threat of TR6, in his later work Kuipers has developed a “refined definition” which, by using a qualitative treatment of similarity, allows that some mistakes are better than other mistakes (see Kuipers 1987b, 2000, Ch. 10).

Cevolani (2016) has shown that Popper had “bad luck” in another sense: if truth and falsity contents are defined as classes of content elements, i.e. negations of state-descriptions, as Rudolf Carnap proposed in his treatment of semantic information, then Popper’s comparative definition is again saved from Miller’s refutation—even though not from the problems with TR4 and TR6.

Schurz and Weingartner (1987) diagnose the failure of Popper’s definition as the problem that a theory is assumed to be closed under all logical consequences. They show that the Miller–Tichý refutation is blocked if the truth content and the falsity contents of a theory A are restricted to its relevant consequences, so that irrelevant disjunctive weakenings and redundant conjunctions are eliminated. It is important that these restricted sets together are logically equivalent to the original theory A.⁷ This modified definition satisfies TR1, TR2, and TR5, but among “completely false theories” (with empty restricted truth content) truthlikeness decreases with logical strength (cf. TR7). Further, as the original version of Schurz and Weingartner’s relevant consequence approach does not satisfy TR4, in their recent work they have supplemented it with a quantitative measure for formulas (see Sect. 5).⁸

3 The similarity approach

A recurring difficulty of attempts to rescue Popper’s definition (1) is that the concepts of truth, falsity, and logical consequence are insufficient to avoid the undesirable consequences TR6 or TR7, and to make sense of the important fallibilist principle TR4. Against approaches relying merely with truth values and logical content or logical consequences, the advocates of the similarity approach employ the notion of similarity or resemblance between (statements describing) states of affairs. The similarity approach was discovered in 1974 independently by Pavel Tichý within propositional logic and Risto Hilpinen within possible worlds semantics (see Hilpinen 1976). Tichý (1974) hinted that a more general solution can be obtained by using Hintikka’s distributive normal forms in predicate logic, which he then was the first to implement in Tichý (1976) for the full polyadic case. In the meantime, the similarity approach was developed in 1975 for monadic predicate logic by Ilkka Niiniluoto (see Niiniluoto 1977) and Tuomela (1978).⁹ Later extensions and debates are summarized in the independently written monographs of Oddie (1986) and Niiniluoto (1987), and in the collection of essays edited by Kuipers (1987a).

Hilpinen (1976) assumed as a primitive notion the concept of similarity between possible worlds. His definition, which compares the minimum distances and the maximum distances of rival theories from the actual world, solves the Miller–Tichý problem with TR5 and satisfies TR6, but it leaves most theories incomparable, and does not satisfy TR4.¹⁰ It satisfies TR2a but not TR2. Niiniluoto (1977), instead, replaces possible worlds by constituents in monadic first-order logic. For a monadic language L with one-place predicates M₁, …, M_k, the Q-predicates Q₁, …, Q_K are defined by conjunctions of the form (±)M₁(x) &···& (±)M_k, where (±) is replaced by the negation sign ∼ or by nothing. Here K = 2^k. A constituent C_i in L expresses which Q-predicates are instantiated and which are not, so that its logical form is

• (4) (±)(Ex)Q₁(x) &···& (±)(Ex)Q_K(x).

If an empty universe is excluded, the number of constituents is 2^K − 1. Let CT_i be the class of Q-predicates which are non-empty by constituent C_i. All generalizations (i.e. quantificational statements without individual constants) can be expressed in a normal form as a disjunction of constituents.

The simplest distance between monadic constituents, due to W. K. Clifford already in 1877, is the number of their diverging claims about the Q-predicates. Thus, the Clifford measure between constituents C_i and C_j is the (normalized) cardinality of the symmetric difference |CT_i Δ CT_j|/K between the classes CT_i and CT_j. Tichý’s (1976) proposal for the polyadic language implied as a special case, against the Clifford measure, that the distance between monadic constituents should take into account the similarities between Q-predicates. This led Niiniluoto in the same year to propose his alternatives to the Clifford measure (see Niiniluoto 1987, pp. 314–321).

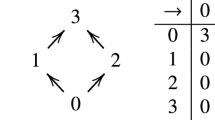
In propositional logic with atomic sentences p, q, and r, a constituent is a sentence of the form (±)p & (±)q & (±)r, where p and ¬p are called literals, and again each sentence has a disjunctive normal form as a disjunction of constituents. According to the Hamming distance, which corresponds to the Clifford measure, the distance between propositional constituents p&q&r and p&¬q&¬r is 2/3 (see Fig. 1 where negation ¬p is denoted by bar ͞p).

Fig. 1

Propositional constituents

As constituents of L are mutually exclusive and jointly exhaustive, there is one and only one constituent C* in L which is true, so that it can be taken to be the target of the definition of truthlikeness. Then the distance of a theory h, which is a disjunction of constituents, should be a function of the distances of its disjuncts from the target C*. Oddie (1986) follows Tichý (1974) in choosing this function to be the average distance Δ_av(C*, h). Inspired by Hilpinen (1976), Niiniluoto (1977) first proposed the weighted average Δ_mm(C*, h) of the minimum and maximum distances. Niiniluoto’s (1987) later min-sum measure Δ_ms(C*, h) differs from the min–max measure by replacing the maximum distance by the normalized sum Δ_sum(C*, h) of all distances of the disjuncts of h from C*:

• (5) $\Delta_{\text{ms}} \left( {{\text{C}}*,{\text{h}}} \right) = \upgamma \Delta_{ \hbox{min} } \left( {{\text{C}}*,{\text{h}}} \right) + \upgamma '\Delta_{\text{sum}} \left( {{\text{C}}*,{\text{h}}} \right),$

where γ > 0 and γ′ > 0 are real-valued parameters indicating our interest in being close to the truth and avoiding falsities. Then the degree of truthlikeness Tr(h, C*) of a theory h relative to the target C* can be defined as 1 − Δ_ms(C*,h). A comparative notion is achieved by defining h to be more truthlike than h′ (relative to target C*) if and only if Tr(h, C*) > Tr(h′, C*).

The examples about the number of planets can be formalized in a monadic language with Q-predicates Q_i(x) = “x has i planets”, for i = 0, …, 100. Then the distance between predicates Q_i and Q_j is |i − j|/100. As Q₈(a) is true for our solar system a, the distance of the claim Q₁₃(a) from the truth is 5/100, and disjunctive claims can be handled with Δ_av or Δ_ms.¹¹

The power of this quantitative similarity approach can be seen in the fact that it makes all generalizations in L comparable for their truthlikeness. Using Jaakko Hintikka’s distributive normal forms, it can be extended to generalizations in full first-order languages with relations, which serves to define a metric in the logical space of complete theories.¹² Another extension is to modal monadic languages with the operator ◊ of physical or nomic possibility, so that nomic constituents have the following form

• (6) (±)◊(Ex)Q₁(x) &···& (±)◊(Ex)Q_K(x).

Distance from the true nomic constituent, using the Clifford measure or its generalizations, gives a solution to the problem of legisimilitude or closeness to the true law of nature (see Niiniluoto 1987, Ch. 11).¹³

The idea of nomic constituents gives a natural reinterpretation of Kuipers’ (1982) original treatment of theoretical verisimilitude (see Niiniluoto 1987, pp. 381–382, 1998; Zwart 2001; cf. Kuipers 2000, p. 305). Instead of discussing models or possible worlds in the condition (3), a theory expresses the possibility of kinds of individuals or structures, so that (3) can be written as a condition on Q-predicates, and the quantitative distance |A Δ T| of a theory A from the truth T (see Kuipers 1987b, p. 88) is equal to the Clifford measure. Later Kuipers (2000) has spoken about “conceptual possibilities”, and in Kuipers (2014) he explicitly adopts the suggestion that these possibilities could be Q-predicates (e.g. black raven, black non-raven, non-black raven, non-black non-raven). This means that a theory for Kuipers is a nomic monadic constituent in the sense (6).¹⁴ In Kuipers (2014) he reformulates his approach so that a theory includes only an exclusion statement, i.e. the conjuncts of (6) with negations (e.g. the law “all ravens are black” excludes the possibility of non-black ravens). This analysis also shows that his later “revised” definition with a notion of “structurelikeness” can be compared to those variants of the Clifford measure which reflect distances between Q-predicates.

Let us still compare the average and min-sum measures as methods of balancing the goals of truth and information in the case of monadic languages. They define truthlikeness in different ways through a “game of excluding falsity and preserving truth” (see Niiniluoto 1987, p. 242, and Table I on p. 234). Both of them satisfy Popper’s condition TR1, i.e.

• (7) Tr(h, C*) = 1 if and only if h is equivalent to the whole truth C*.

If h is false, then Tr(h v C*, C*) > Tr(h, C*), so that they both satisfy TR3. Both avoid Miller’s refutation of Popper, so that TR5 is satisfied. Further, both are able to handle false theories so that TR6 and TR7 are satisfied: comparison of false theories depends on the distances of the false disjuncts from the truth.

Some of the properties of the min-sum measure depend on the choice of the parameters γ and γ′. Note that the average distance of a tautology t from the truth C* is 1/2, so that Δ_av satisfies TR4. For the min-sum measure, Tr(t, C*) = 1 − γ′ for a tautology t. It follows that a false constituent C_i is less truthlike than the weakest true theory (i.e. worse than ignorance) if its distance from the truth is larger than γ′/γ. Such answers can be called misleading, while those better than ignorance are truth-leading. If the weight γ for the truth factor is large, no constituent is better than t. If the weight γ′ for the information factor is large, all constituents are better than t.¹⁵ This gives a practical guide for choosing the weights γ and γ′ so that TR4 is satisfied. For example, the choice γ ≈ 2γ′ implies that in Fig. 1 the truth-leading answers are within a circle with radius 1/2 from the complete truth, and the misleading answers are outside this circle (see Niiniluoto 1987, p. 232).

Zwart (2001) notes that the followers of Popper’s explication give “content definitions” in the sense that the least truthlike of all theories is the negation ~ C* of complete truth C* (i.e. the disjunction of all false constituents), while the “likeness definitions” imply that the worst theory is the “complete falsity” (i.e. the constituent at the largest distance from the truth). For suitable choices of the weights, e.g. γ′/γ close to 1/2, the min-sum measure gives a likeness definition (see Niiniluoto 1987, p. 232; 2003). Zwart and Franssen (2007) use Arrow’s theorem to argue that content and similarity definitions cannot be merged to give a truthlikeness ordering. Oddie (2013, p. 1670), thinks that the principle TR2 expresses the core of “content measures”, suggesting that the min-sum measure is a “likeness—content compromise”. According to his constraints, “strong” likeness definitions should accept the average measure. But, in fact, the min-sum definition shows that a likeness or similarity account can satisfy both TR2 (called “the value of content for truths” by Oddie) and TR5 (thus avoiding “the value of content for falsehoods”).

Niiniluoto (1987, pp. 418–419), points out that for the trivial or “flat” distance function, which takes all false constituents to be equally distant from the truth, the min-sum measure reduces to Levi’s (1967) measure of epistemic utility. Levi’s measure turns out to be a typical case of a content-based measure of closeness to truth (weighted average of truth value and content measured relative to an even probability distribution), which violates TR4 and TR6. This shows the compatibility of the min-sum measure with the content approach, but only in the extreme case of flat distance or “likeness nihilism” (cf. Oddie 2013, p. 1675).

The debate about Popper’s principle TR2 is the main difference between the average approach of Oddie (1986) and the min-sum approach of Niiniluoto (1987). Namely, Δ_av violates TR2 and TR2a by allowing that a true theory can be improved by adding to it new false disjuncts, if the average distance is thereby decreased: for example, “8 or 13 or 20” is better that “8 or 20” as an answer to the question about the number of planets.¹⁶ In contrast, Δ_ms sees here the addition of “13” as superfluous, once we already have hit upon the truth “8”. In a game of finding truth and excluding falsity, a theory can be seen as a set of alternative guesses about the target. Even though the theory does not endorse the false guesses conjunctively but allows them (see Oddie 2013, p. 1671), still every falsity included in a theory is a mistake whose seriousness depends on its distance from the target. In this game, we try to hit the true constituent as soon as possible (cf. TR1). After several shots, our score depends on our best result (Δ_min) and the sum of all the mistakes (Δ_sum). Thus, this measure is based on a general principle of penalty: in calculating the distance from the truth, you have to pay for all of your mistakes. But this penalty is to some extent compensated, if we succeed in improving our best result so far.

The min-sum measure Δ_ms is an improvement of the min–max measure Δ_mm, which satisfies only the weaker TR2a, since it takes into account what happens in the theory between the best and worst guesses. In particular, a theory becomes worse when equally false new disjuncts are added to it:

• (TR8) If C_i and C_j are equally distant from the truth, i ≠ j, then Tr(C_i ∨ C_j, C*) < Tr(C_i, C*).

This is called “thin better than fat” by Niiniluoto (1987, p. 233). Another important principle is that adding a new disjunct improves a theory only if the minimum distance is at the same time decreased (see M8 in Niiniluoto 1987, p. 233). Adding a new disjunct leads to a loss of information-about-the-truth which can be compensated only by at the same time improving the minimum distance from the truth:

• (TR9) Tr(h v C_i, C*) > Tr(h, C*) if and only if C_i is closer to the truth than the minimum of h.

This principle is satisfied by the min-sum measure, when γ is sufficiently large in relation to γ′ (ibid., pp. 230–231).

Oddie returned to this debate in his 2014 revision of his 2001 survey of truthlikeness in Stanford Encyclopedia of Philosophy (see Oddie 2013, 2014). He has no hesitation in the continuing rejection of the principle TR2, which he attacks indirectly by an ingenious derivation of the average measure from three axioms. The first of them is the “uniform distance principle”:

• (AV1) If C_i and C_j are equally distant from the truth, i ≠ j, then Tr(C_i ∨ C_j, C*) = Tr(C_i, C*).

This seems to be tailor made for average, as it directly contradicts TR8. For example, AV1 implies that “4 or 12” and “12” are equally truthlike answers to the question about the number of planets.¹⁷ In the two-dimensional problem of locating a city on a map, with the Euclidean distance, the full circle around 〈0, 0〉 with radius 1 (or any of its parts) is equally truthlike as the point 〈0, 1〉. Similarly, in Fig. 1 p${\bar{\text{q}}}$r v ${\bar{\text{p}}}$qr and ${\bar{\text{p}}}$qr are equally truthlike by AV1. This could be valid for minimum distance, which excludes all content considerations and defines the notion of approximate truth in Hilpinen’s (1976) sense, but not for a notion of verisimilitude based on the penalty principle. One peculiarity of AV1 is that its conclusion fails, if a third closer constituent is added to the disjunction: if C_i and C_j are equally distant from the truth and farther from the the truth than C_k, then the average measure and the min-sum measure agree that Tr(C_i v C_j v C_k, C*) > Tr(C_i v C_k, C*).

Oddie’s second assumption is the “weak pareto principle”:

• (AV2) If C_j is at least as close to the truth as C_i, then Tr(h(j/i), C*) ≥ Tr(h, C*),

where h(j/i) is the result of substituting C_i in theory h by C_j. This is valid for the min-sum measure by the penalty principle: for its special case, “ovate better than obovate”, see M12 in Niiniluoto (1987, p. 233). The third axiom is the “difference principle”:

• (AV3) The difference in the degrees of truthlikeness of h and h(j/i) depends only on C_i and C_j and the number of constituents in the normal form of h.

But it can claimed that the location (not only the number) of constituents in the normal form of h is relevant: in the planet case, the shift from “14 or 15 or 20” to “13 or 15 or 20” is more dramatic than the shift from “10 or 14 or 15” to “10 or 13 or 15”, since the former improves the best guess of the theory. This objection is not based on the endorsement of Δ_min as an adequate measure of truthlikeness, as Oddie’s reply suggests (Oddie 2013, p. 1674), but rather on the principle TR9 satisfied by Δ_ms.

If your intuitions are in favor of TR2, TR8, and TR9, and you are not willing to accept the special principles AV1 and AV3, then Oddie’s argument for the average function is not compelling.

The definition of truthlikeness is not only an exercise of logical intuitions, but it can be assessed also from the viewpoint of the intended applications of this notion in the philosophy of science. For Popper (1963) the two main applications were the falsificationist methodology and scientific progress. First, it is natural to expect that the elimination of false hypotheses should increase truthlikeness. But this idea needs a qualification: if our current hypothesis is the disjunction of two false theories A and B, where A is closer to the truth than B, then the elimination of A does not increase truthlikeness. This result is delivered both by Δ_ms and Δ_av. If we falsify our only hypothesis A, and are left with a tautology or ¬A, then by TR4 we may have a loss in verisimilitude. In order to gain in truthlikeness, the falsified hypothesis should be replaced by a more truthlike alternative. But suppose that our hypothesis is A v B v C, where A is true. Then the falsification of B should increase truthlikeness. This requirement follows from Δ_ms by TR2, while it may fail in some cases for Δ_av.

Secondly, scientific progress in the objective realist sense be can explicated by increasing truthlikeness, and scientific regress by decreasing truthlikeness (Niiniluoto 1984). Adequacy conditions TR1–TR7 have a natural interpretation as principles of progress. For example, TR4 states that science has been progressive with false but truthlike theories: it is better to have Newton’s theory than to be ignorant about mechanics, and by TR5 it is still better to replace Newton’s theory with Einstein’s special theory of relativity. One relevant comparison is between principles TR8 and AV1: are we making regress, if a theory is weakened by adding a new disjunct without a gain in closeness to the truth? But the most dramatic examples concern the violation of TR2 by the average measure. According to the cumulative principle TR2, adding conjunctively a new truth to an old truth is an instance of scientific progress. This result is delivered by the min-sum measure. Advocates of the average measure, who disagree with this conclusion, should explain what they mean by progress—or alternatively deny that the notion of truthlikeness is applicable to the axiological problem of characterizing progress in science.

4 Convergence: conjunctive theories

In the similarity approach, theories are represented as disjunctions of constituents. Such normal forms are generalizations of the disjunctive normal form in propositional logic. Schurz and Weingartner (2010) use instead conjunctive normal forms, where theories are conjunctions of content elements. Schurz (2011) observes that the “basic feature approach” developed by Roberto Festa and Gustavo Cevolani also belongs to the conjunctive camp.¹⁸ It is restricted to c-theories or convex conjunctive theories, which are generalizations of constituents in propositional logic, i.e. statements about atomic sentences with some definite positive claims, some negative claims, and some left open. Then a c-theory h is more verisimilar than another c-theory h′ if h makes more true claims and less false claims than h′. This is again a variant Popper’s criterion (1) and defines a qualitative partial ordering. A quantitative verisimilitude measure V is c-monotonic if it agrees with this qualitative ordering. Inspired by Amos Tversky’s similarity metrics,¹⁹ Festa and Cevolani have developed a c-monotonic “basic feature approach”, where the verisimilitude of a c-theory depends on its matches and mismatches in relation to the true constituent (see Cevolani et al. 2013). They also note that this quantitative measure, when restricted to c-theories, agrees with many existing measures, like average, min–max, and refined relevant consequences.²⁰ But the claim that the min-sum measure is not c-monotonic (see Cevolani et al. 2011, p. 188) is mistaken, since the supposed counterexamples involve inadmissible choices of parameters.²¹

Propositional c-theories can be immediately generalized to monadic predicate logic (see Niiniluoto 2011). Such conjunctive theories include those statements which make definite existence claims about some Q-predicates, non-existence claim about some Q-predicates, but may leave some Q-predicates open. This class includes purely universal generalizations and purely existential statements. Monadic constituents are a special case, where the claims leave no question marks about the cells. Tuomela (1978) defined the distance of such generalizations from the true constituent directly by a function which compares their claims about the Q-predicates, so that his approach in fact initiated the basic feature approach. For constituents, this distance includes the Clifford measure as a special case (see Niiniluoto 1987, pp. 319–321). Following Oddie (1986, p. 86), Festa (2007) calls such monadic c-theories “quasi-constituents”, and extends their treatment to statistical hypotheses.

As monadic c-theories can be expressed as disjunction of constituents, their degree of truthlikeness can be calculated by the min-sum measure. In Fig. 2 we have a generalization g_i with positive claims in PC_i, negative claims in NC_i, and question marks in QM_i, whereas CT* includes the existence claims of the true constituent. Then the min-sum measure gives a general formula which shows that the distance of such a generalization from the truth increases with c−c′ (the number of wrong existence claims), b′ (the number of wrong non-existence claims), and m (its informational weakness):

$$ (\upgamma + 2\upgamma '/2^{\text{K-m}} )\frac{{\left( {c - c' + b'} \right)}}{K} -\upgamma '{\text{m/K2}}^{\text{K-m}} $$

(see Niiniluoto 1987, p. 337). Apart from some coefficients this is essentially the same as the result by the balanced contrast measure (with ϕ = 1):

$$ \left[ {2\left( {{\text{c}}{-}{\text{c}}^{\prime } + {\text{b}}^{\prime }} \right) + {\text{m}}} \right] / {\text{K}}. $$

So there is no deep difference between the disjunctive approach by normal forms and the conjunctive approach by basic features.

Fig. 2

Monadic c-theory

Recent work on conjunctive theories shows that there is perhaps surprising convergence in the rival approaches to truthlikeness. One of the remarkable results is that Popper’s TR2, which Tichý and Oddie have heavily criticized, holds for their average measure Δ_av when applied to c-theories:

• (8) When restricted to c-theories, the average measure satisfies TR2.

This means that the average and min-sum measures give the same truthlikeness ordering of pairs of true c-theories when one of them is logically stronger than the other.²²

Another important result concerns the relations of truthlikeness and belief revision. The basic observation is that a false belief system B may become less truthlike, when it is expanded or revised by a true input A. For example, let B state that the number of planets is 9 or 20 and A that this number is 8 or 20; then the expansion of B by A states that this number is 20. If the original theory B′ claims that this number is 19, then the revision of B′ by A is 20 (see Niiniluoto 2011). But it can be shown that convex c-theories avoid this problematic conclusion:

• (9) For a c-theory B and c-theory input A, if A is true, then the expansion and revision of B by A increase the truthlikeness of B.

(See Cevolani et al. 2011; Niiniluoto 2011.)

On the other hand, even though c-theories behave in a nice way, one should emphasize that all statements are not conjunctive in this sense. For example, in propositional logic disjunctions p v q and implications p → q are not convex, and in predicate logic the generalizations (x)(Fx → (Gx v Hx)), (Ex)(Rx & (Gx v Hx)) and (x)(Cx → (Fx ↔ Hx)) are not convex. The methodological superiority of the disjunctive approach can be seen in its ability to treat all statements with different logical forms in qualitative and quantitative first-order (and even higher-order) languages.

But as soon as we go beyond c-theories, the consensus breaks down. Cevolani and Festa (2018) propose an extension of their basic feature approach in terms of partial consequences, and it turns out that this leads to a measure which is ordinally equivalent to the average measure. So they are able to apply their extended measure to any statements in the propositional language, but the violation of TR2 forces them to reconsider their earlier work on scientific progress and belief revision. In particular, even what Niiniluoto (2011) regarded as the only “safe case” of increasing truthlikeness, viz. the expansion of a true belief system by a true input, is not generally valid any more. For example, if we correctly believe that the number of planets is 8 or 13 or 20, and we expand this belief by the true input that this number is not 13, then the conclusion “8 or 20” is less truthlike by the average measure (but not by the min-sum measure).

In the final section, we still have to assess the refined conjunctive treatment by Schurz and Weingartner (2010), which is not restricted to c-theories.

5 The problem of false disjunctions

After considering some disagreements about true disjunctions (cf. TR2), we are now ready to return to the old debate about false disjunctions, introduced in Sect. 1. Recall that Schurz and Weingartner (1987) use the relevant consequence relation to analyze theories into their conjunctive components. Let A_t be the true conjunctive parts of A and A_f its false components. Then, modifying Popper’s criterion (1), A is at least as verisimilar as B if and only if

• (10) A_t ⊢ B_t and B_f ⊢ A_f.

In their quantitative treatment for propositional languages with n atomic sentences, Schurz and Weingartner (2010) define a measure V which ordinally agrees with the partial ordering (10). For a theory A, the measure V(A) is the sum of the V-values of all conjunctive parts of A. For literals, where p is true, V(p) = 1 and V(¬p) = −1. The V-value of a tautology t is 0, and that of a contradiction –(n + 1). Further,

$$ \begin{aligned} {\text{V}}\left( {\text{a}} \right) & = \frac{va}{ka}.\frac{{\left( {n - ka + 1} \right)!}}{n!}\quad {\text{for a in A}}_{\text{t}} \\ {\text{V}}\left( {\text{a}} \right) & = - \frac{{\left( {n - ka + 1} \right)!}}{n!} \quad {\text{for a in A}}_{\text{f}} ,\\ \end{aligned} $$

where k_a is the number of a’s literals and v_a is the number of a’s true literals. It follows that for a true disjunction V(p₁ v p₂) = 1/n, and for a completely false theory (with an empty A_t)

$$ {\text{V}}(\neg {\text{p}}_{1} \;{\text{v}} \ldots {\text{v}}\;\neg {\text{p}}_{\text{k}} ) = - {\text{V}}\left( {{\text{p}}_{1} \;{\text{v}} \ldots {\text{v}}\;{\text{p}}_{\text{k}} } \right). $$

It immediately follows that the refined account of Schurz and Weingartner agrees with their old approach about false disjunctions: among completely false theories verisimilitude decreases with logical strength (see Schurz 2011, p. 208). This means that the V-function violates the adequacy condition TR7.

If the value function V is applied to the sentences in Fig. 1, we obtain

$$ \begin{aligned} & {\text{V}}(\neg {\text{p}}\& \neg {\text{q}}\& \neg {\text{r}}) = - 1 - 1 - 1 = - 3 \\ & {\text{V}}(\neg {\text{p}}\& \neg {\text{q}}) = - 1 - 1 = - 2 \\ & {\text{V}}(\neg {\text{p}}) - 1 \\ & {\text{V}}({\text{p}}\& \neg {\text{q}}\& \neg {\text{r}}) = 1 - 1 - 1 = - 1 \\ & {\text{V}}\left( {\text{t}} \right) = 0 \\ & {\text{V}}({\text{p}}\& {\text{q}}\& \neg {\text{r}}) = 1 + 1-1 = 1. \\ \end{aligned} $$

Here V agrees with the ordering of the constituents by the min-sum measure Tr relative to the target pqr, stronger falsities in this list are less truthlike, and (with admissible values of parameters) the division between truth-leading (positive V) and misleading (negative V) is the same. Since ¬p&¬q&¬r is the least truthlike of all consistent sentences, measure V defines a likeness ordering in Zwart’s (2001) sense. But differences between these measures appear in the case of false disjunctions:

$$ {\text{V}}(\neg {\text{p}}) = - 1 < - 1/3 = - {\text{V}}\left( {\text{p v q}} \right) = {\text{V}}(\neg {\text{p v}}\neg {\text{q}}),{\text{ but Tr}}(\neg {\text{p}}) > {\text{Tr}}(\neg {\text{p v}}\neg {\text{q}}). $$

The latter inequality for Tr follows from the condition that ¬p v ¬q has the same minimum distance 1/3 from p&q&r as ¬p but it has to pay penalties for the constituents (i.e. p͞qr and p͞q͞r) which it adds to the normal form of ¬p. Differences can be found also among partially true theories:

$$ \begin{aligned} & {\text{V}}({\text{p}}\& (\neg {\text{q v}}\neg {\text{r}})) = 1-1/3 = 2/3 > 0 = {\text{V}}({\text{p}}\& \neg {\text{q}}), \\ & {\text{but Tr}}({\text{p}}\& (\neg {\text{q v}}\neg {\text{r}}) < {\text{Tr}}({\text{p}}\& \neg {\text{q}}). \\ \end{aligned} $$

The argument for Tr(¬p) > Tr(¬p v ¬q) follows directly from the min-sum definition, so that it is not based on any assumption about the relative distances of the false disjuncts from the truth. Indeed, here Tr(¬p) = Tr(¬q) holds by symmetry. So this example is different from the case of false estimates of the number of planets, discussed in Sect. 1. As the new approach by Schurz assumes that all true literals have the same V-value, and similarly for false literals, it does not tell how problems of numerical approximation could be handled in the relevant consequence approach.

It is interesting to observe that Oddie’s average measure, in spite of its acceptance of the uniform distance principle AV1, agrees in this case with Schurz’s judgment. Even though ¬p and ¬q have the same average distance 2/3 from the truth pqr, the average distance for ¬p v ¬ q is 11/18, which is less than 2/3. This follows from the fact that the two additional constituents in the normal form of ¬p v ¬q in fact reduce the average distance. Cevolani and Festa (2018), whose “partial consequence approach” agrees with Oddie’s average measure, also support Schurz’s conclusion that the logically weaker of two false disjunctions is more truthlike.

In conversation, Schurz raised the following question: assuming that (x)Fx is true, is the weaker falsity (Ex)¬Fx closer to the truth than the stronger falsity ¬Fa? To formalize this problem, let language L include one monadic predicate F and two individual constants a and b. Then the truth in L is expressed by Fa & Fb. The statement ¬Fa is equivalent to the disjunction (¬Fa&Fb) v (¬Fa&¬Fb), while (Ex)¬Fx adds to this disjunction one more false disjunct Fa&¬Fb. Therefore, by the min sum measure with the target (x)Fx, we have Tr(¬Fa) > Tr((Ex)¬Fx). One might think otherwise, and follow Schurz’s principle that here verisimilitude should decrease with logical strength, but this intuition would probably reflect the idea that a definite mistake about a concrete given individual a is somehow more serious than an indefinite claim about some individual just existing out there. But that consideration would lead us back to the situation where the false disjuncts are at different distances from the truth. While most of us would agree that the stronger answer “2” is closer to the truth about the number of moons than the weaker answer “2 or 2000”, the comparison between “99 or 100 or 2000” and “99 or 2000” is more controversial – at least different answers would be given by Oddie and Niiniluoto (cf. TR9).

Let us finally see how Kuipers would solve the problem of false disjunctions. Note first that such false statements cannot be represented as constituents or c-theories, so that his new approach is not applicable. But if we go back to his early approach (3) and represent theories in propositional logic as sets of constituents,²³ then, interestingly enough, his early and later accounts give diverging answers. The “naïve” definition of Kuipers (1982) suffers from the child’s play objection, so that by the modified symmetric difference criterion (3) the stronger falsity ¬p is closer to the truth than the weaker ¬p v ¬q. Here Kuipers agrees with the min-sum judgement (but for a different reason) and disagrees with Schurz. According to the refined account, theory A is at least as truthlike as theory B if

• (11) For all x in B and all z in T there is y in A such that s(x, y, z)

• (12) For all y in A-(B ∪ T) there are x in B-T and z in T-B such that s(x, y, z),

where s(x, y, z) means that y is between x and z, i.e. y is at least similar to z as x (see Kuipers 2000, p. 250). As here the true theory T consists only of the true constituent C*, these conditions for false theories A and B can be simplified to

• (11′) For all x in B there is y in A such that s(x, y, C*)

• (12′) For all y in A there is x in B such that s(x, y, C*).

Taking now A as ¬p v ¬ q and B as ¬p, conditions (11′) and (12′) are satisfied, so that A is at least as close to the truth as B. But for the constituent p͞qr in A there is no element x in B such that s(p͞qr, x, C*). Hence, A is in fact more truthlike than B by the revised definition of Kuipers. This agrees with the judgment of Schurz, so that both of them reject TR9, and thus disagree with the min-sum approach.

For cases where x and y are real numbers or natural numbers, the relation of betweenness s(x, y, z) could be explicated by the geometrical distance, i.e. s(x, y, z) if and only if |y–z| ≤ |x–z|.²⁴ Then (11′) is satisfied if the minimum distance of A to C* is smaller than or equal to the minimum distance of B to C*. Likewise, (12′) is satisfied if the maximum distance of A to C* is smaller than or equal to the maximum distance of B to C*. In this interpretation, the refined account of Kuipers would agree with Hilpinen’s (1976) comparative notion of truthlikeness. Therefore it could violate the stronger form of TR2, and it would satisfy Oddie’s uniform distance principle AV1, which is not valid for the min-sum measure. But if s(x, y, z) means that y is between x and z, so that z ≤ y ≤ x or x ≤ y ≤ z (see Kuipers 2000, p. 249), then AV1 is not satisfied. For both interpretations, Kuipers would agree that “9” is better than “9 or 20” as the number of planets, but he would allow that “9 or 20” and “9 or 12 or 20” are equally good as “9 or 19 or 20”, in disagreement with both Δ_av and Δ_ms.²⁵

These examples thus give us good reasons to continue old and new debates about the definition of truthlikeness.