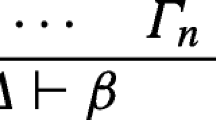Abstract
Although the case for the judgment-dependence of many other domains has been pored over, surprisingly little attention has been paid to mathematics and logic. This paper presents two dilemmas for a judgment-dependent account of these areas. First, the extensionality-substantiality dilemma: in each case, either the judgment-dependent account is extensionally inadequate or it cannot meet the substantiality condition (roughly: non-vacuous specification). Second, the extensionality-extremality dilemma: in each case, either the judgment-dependent account is extensionally inadequate or it cannot meet the extremality condition (roughly: absence of independent explanation). The paper concludes with a moral concerning the judgment-dependence of a posteriori areas of discourse that emerges from consideration of these two a priori cases.
Similar content being viewed by others
Notes
‘Equation’ is a misnomer, as the formula does not contain a leading identity symbol. The terminology of response-dependence versus response-independence (of which judgment-dependence versus judgment-independence is a special case) is in fact due to Mark Johnston (1989). Wright, who acknowledges Johnston as the source for many of these ideas (1993, p. 109), prefers the terminology ‘extension-determining versus extension-reflecting’. Pettit (1991) has also put forward an important version of the distinction. The differences between these three accounts are discussed in Wright (1992, pp. 135–139) and will not much matter here.
The account can be developed and refined in several ways. For example, one could include reference in the right-hand side not just to a single subject S but to a collection of subjects. A Rawlsian, say, might explicate what it is for a state to be just in terms of collective judgments. As is often noted, in some cases (but not those of mathematics and logic) the obtaining of the conditions C could causally affect the subject’s judgment that x is F.
Compare Mark Johnston’s ‘missing explanation’ argument (1993, p. 94 ff.).
If an F-detector is defined as anything that infallibly detects F-ness the substantiality condition would not be met.
The judgment-dependence/judgment-independence distinction, or more generally the response-dependence/response-independence distinction, has been seen by some as a reasonable way of spelling out the primary/secondary quality distinction, e.g. by McDowell (1985), Wright (1992, p. 81), Johnston (1993). The fit is admittedly not perfect; for example, judgment-dependence is not happily seen as explicating the error-theoretic strands of early modern discussions by Galileo and Locke of secondary qualities. Nevertheless, the two distinctions appear to have roughly the same demarcation as their target. It is also worth noting that a judgment-dependent account is not necessarily relativist. If a Martian, differently constituted from us, does not judge our best jokes to be funny, then according to the account the Martian is simply mistaken.
“I would also anticipate that arithmetic will fail order-of-determination [spelled out as judgment-dependence on p. 77]. But that is an expression of the conviction that Platonism is untenable. For the essential epistemology of Platonism is exactly the view that mathematical propositions pass the order-of-determination test” (1993, pp. 82–83).
Following Wright’s model of judgment-dependence they then declare (their italics): “Our central two-fold claim is that mathematical belief is reliable because mathematical truth is judgement-dependent, and that the judgement-dependence of mathematical truth brings no commitment to the mind-dependence of mathematical objects.” (1999, p. 280).
Not deviously coded, nor presented as the statement inscribed in some physically inaccessible location, etc.
Wright for instance presupposes decidability as a necessary condition for judgment-dependence: “A natural starting point [for how an instance of the Euthyphro debate might properly be conducted] would be the question whether the decidability of the statements in question was assured only as a matter of contingency or—closely relatedly—whether the coincidence of truth with superassertibility within the discourse was something that could be known only a posteriori” (1992, p. 81).
Despite the simple-mindedness of this dilemma, Divers and Miller (1999) surprisingly do not mention it, nor does Wright do so in his discussion of arithmetical judgment-dependence (1993, pp. 82–83). Johnston (1993, pp. 88–89) cites Gödel’s and Tarski’s theorems as showing that there is no single ideal theory, but at best an indefinitely extensible hierarchy of them. Though he does not directly apply these results to the question of mathematics’ judgment-dependence (nor does he consider logic), the tenor of Johnston’s remarks suggests that he would be sympathetic to the present article. For proofs of most of the metamathematical results invoked in this article, consult Boolos et al. (2007).
Hence this is not even dialetheism; it is analetheism.
This might be Divers and Miller’s (1999) view given that their discussion of mathematical truth focuses on elementary arithmetic.
Nor will the manoeuvre of taking a set-theoretic statement to be true if it is true in all models of ZFC2, since this no longer constitutes a judgment-dependent account.
For an exposition, see Shapiro (1991, ch. 5).
See Weston (1976).
There is an asymmetry with the basic equation for is a first-order logical truth since we do not assume that an ideal reasoned is conscious of all her incapacities as well as capacities. This is why the right-hand side is not ‘‘the ideal reasoner could not infer that x from no premisses’.
In the sense that {γ1,…,γ n } ⊨ δ and {γ1,…,γ n } ⊢ δ are decidable facts.
Indeed, so far as the traditional proponent of the ontological argument is concerned, to suggest so in the theological case would be tantamount to blasphemy.
Something like the analyticity condition has seemed natural to those sympathetic to judgment-dependent accounts. The longer passage from which Wright’s quote in Sect. 1 was extracted is: “the truth, if it is true, that the extensions of colour concepts are constrained by idealised human response—best opinion—ought to be accessible purely by analytic reflection on those concepts, and hence available as knowledge a priori” (Wright 1992, pp. 116–117); “It seems current orthodoxy that one who grasps a concept of a particular secondary quality, e.g. redness, can discover a priori by analysis that the conception is of a secondary rather than a primary quality.” (Edwards 1992, p. 263).
There is no need for a more precise definition.
Anyone who is tempted to deny that modus ponens is a rule that holds in virtue of meaning or that logical truth are not true in virtue of meaning is presumably a sceptic about analyticity in the first place.
Do not confuse ‘it is a deductive logical truth that p’ (or ‘Dp’) with ‘there is a proof in some specified axiom system of the formalisation of p’ (or ‘⊢p’ as we might write it). The latter is a statement about syntax and would not standardly be construed as a logical truth (e.g. it is an existential statement). Neither of these should be confused with the arithmetical codification of ‘⊢p’ using Gödel numbering, which is an arithmetical truth.
References
Boolos, G., Burgess, J. P., & Jeffrey, R. (2007). Computability and logic (5th ed.). New York: Cambridge University Press.
Divers, J., & Miller, A. (1999). Arithmetical Platonism: Reliability and judgment-dependence. Philosophical Studies, 95, 277–310.
Edwards, J. (1992). Secondary qualities and the a priori. Mind, 101, 263–272.
Gödel, K. (1946). Remarks before the Princeton bicentennial conference on problems in mathematics. In S. Feferman, et al. (Eds.), Collected works, Vol. 2 (pp. 150–153). Oxford: Oxford University Press.
Johnston, M. (1989). Dispositional theories of value. Proceedings of the Aristotelian Society Supplementary, 63, 139–174.
Johnston, M. (1993). Objectivity refigured: Pragmatism without verificationism. In J. Haldane & C. Wright (Eds.), Reality, representation and projection (pp. 85–130). Oxford: Oxford University Press.
Koellner, P. (2006). On the question of absolute undecidability. Philosophia Mathematica, 14, 153–188.
Levy, A., & Solovay, R. M. (1967). Measurable cardinals and the continuum hypothesis. Israel Journal of Mathematics, 36, 234–248.
McDowell, J. (1985). Values and secondary qualities. In T. Honderich (Ed.), Morality and objectivity (pp. 110–129). London: Routledge.
Pettit, P. (1991). Realism and response-dependence. Mind, 100, 587–626.
Shapiro, S. (1991). Foundations without foundationalism. Oxford: Clarendon Press.
Tarski, A. (1951). A decision method for elementary algebra and geometry (2nd ed.). Berkeley and Los Angeles: University of California Press.
Weston, T. (1976). Kreisel, the continuum hypothesis and second-order set theory. Journal of Philosophical Logic, 5, 281–298.
Wright, C. (1992). Truth and objectivity. Cambridge, MA: Harvard University Press.
Wright, C. (1993). Realism: the contemporary debate: W(h)ither now? In J. Haldane & C. Wright (Eds.), Reality, representation and projection (pp. 63–84). Oxford: Oxford University Press.
Acknowledgments
This paper was written in 2005 under the welcoming roof of the New York Public Library. I am grateful to audiences at the 2005 Bristol Logic Colloquium, the Oxford Philosophy of Mathematics Seminar and the Oxford Philosophical Society for subsequent discussion, and to Mark Sprevak and Ralph Wedgwood for comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Paseau, A. Against the Judgment-Dependence of Mathematics and Logic. Erkenn 76, 23–40 (2012). https://doi.org/10.1007/s10670-011-9320-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-011-9320-0