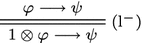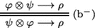Skip to main content
SpringerLink
Log in

Studies in the logic of K-onfirmation

  • Published:
Philosophical Studies Aims and scope Submit manuscript

Abstract

This research article revisits Hempel’s logic of confirmation in light of recent developments in categorical proof theory. While Hempel advocated several logical conditions in favor of a purely syntactical definition of a general non-quantitative concept of confirmation, we show how these criteria can be associated to specific logical properties of monoidal modal deductive systems. In addition, we show that many problems in confirmation logic, such as the tacked disjunction, the problem of weakening with background knowledge and the problem of irrelevant conjunction, are also associated with specific logical properties and, incidentally, with some of Hempel’s logical conditions of adequacy. We discuss the raven paradox together with further objections against Hempel’s approach, showing how our analysis enables a clear understanding of the relationships between Hempel’s conditions, the problems in confirmation logic, and the properties of deductive systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. This understanding of inconsistency is related to the principle that from the false, everything follows (in this case, ex contradictione quodlibet). Since, as we will see, this principle can be removed from a deductive system, we will rather say that two formulas are inconsistent when they logically imply the constant representing falsehood (i.e., 0).

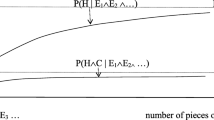
  2. And e is neutral with respect to h if it neither confirms nor disconfirms it.

  3. The notation for the rules (\(\otimes\)-out) and (\(\oplus\)-out) is an abbreviation that includes two separate rules in each case.

  4. Given the flexibility of monoidal logics, note that these definitions could be more general and simply require that \({\mathcal {D}}\) be a deductive system.

  5. \(\varphi \cong \psi\) stands for both \(\varphi \longrightarrow \psi\) and \(\psi \longrightarrow \varphi\). It represents logical equivalence.

  6. See Garson (2006) for how to build a counter-model. Write \(\vdash\) instead of \(\longrightarrow\) and use the usual connectives. Assume that h is a logical consequence of e (hence it holds in every scenario w). Then, there are x and v such that xRv (with R a reflexive and euclidian relation) and \(a_x(e) = \top\) but \(a_x (\Box h) =\bot\), while \(a_v (h) = \bot\), \(a_v(e\supset\)h\()=\top\) and \(a_v(e) =\bot\).

  7. It is also logically equivalent to \(\Box \varphi \longrightarrow \lnot \Box \lnot \varphi\).

  8. As a notational convention, we write, for example, (D, cut) within a derivation as a justification to shorten the notation. It means that there would be another branch in the derivation, with the proper instance of (D), and then (cut) would be used.

  9. The imprecise conception of confirmation has been objected to Hempel. See Huber (2008) for a summary.

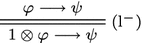
  10. figure k

    .

  11. \(\psi\) is contradictory if \(\lnot \psi\) is analytic, hence if \(1 \longrightarrow \lnot \psi\). From the definition of negation, (cl) and (l\(^-\)) we get that \(\psi\) is contradictory when \(\psi \longrightarrow 0\).

  12. Hypothetico-deductivists assume a converse entailment condition instead of Hempel’s entailment condition (see Sect. 5.1.3 below). Given that it is a distinct view on confirmation logic, we will not analyze this literature and we refer the reader to Gemes (1998) for an overview of hypothetico-deductivism.

  13. See also Moretti (2006) for a thorough discussion of tacked disjunction.

  14. See also Hawthorne and Fitelson (2004). This problem is often analyzed in light of a quantitative concept of confirmation (cf. Crupi and Tentori 2010).

  15. This strategy to solve the paradox was also suggested earlier by Swinburne (1971), although it is not the one he adopted.

  16. Note that Sylvan and Nola (1991, p. 8) argued that the source of the equivalence \((R x \oplus \lnot R x)\,\multimap \;(\lnot R x \oplus B x) \cong R x\,\multimap \;B x\) was that \(\varphi\,\multimap \;\psi\) and \(\lnot (\varphi \otimes \lnot \psi )\) are logically equivalent (this is actually one of their motivation if favor of a relevant implication). This however, is misleading. Indeed, \(\varphi\,\multimap \;\psi \cong \lnot (\varphi \otimes \lnot \psi )\) holds within a SCC co S while \((\varphi \oplus \lnot \varphi )\,\multimap \;(\varphi\,\multimap \;\psi ) \cong \varphi\,\multimap \;\psi\) does not.

  17. From a categorical perspective, this can be derived as soon as \(\multimap\) is an adjoint to \(\otimes\).

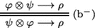
  18. figure ah

    .

References

  • Chellas, B. F. (1980). Modal logic: An introduction. Cambridge: Cambridge University Press.

    Book  Google Scholar 

  • Crupi, V. (2015). Confirmation. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy. Palo Alto: Stanford University.

    Google Scholar 

  • Crupi, V., & Tentori, K. (2010). Irrelevant conjunction: Statement and solution of a new paradox. Philosophy of Science, 77(1), 1–13.

    Article  Google Scholar 

  • Crupi, V., Tentori, K., & Gonzalez, M. (2007). On bayesian measures of evidential support: Theoretical and empirical issues. Philosophy of Science, 74(2), 229–252.

    Article  Google Scholar 

  • Fitelson, B. (2002). Putting the irrelevance back into the problem of irrelevant conjunction. Philosophy of Science, 69(4), 611–622.

    Article  Google Scholar 

  • Fitelson, B. (2006). The paradox of confirmation. Philosophy Compass, 1(1), 95–113.

    Article  Google Scholar 

  • Fitelson, B., & Hawthorne, J. (2010). How Bayesian confirmation theory handles the paradox of the ravens. In E. Eells, J. H. Fetzer (Eds.), The place of probability in science: In honor of Ellery Eells (1953–2006) (pp. 247–275). Springer: Dordrecht.

  • Garson, J. (2006). Modal logic for philosophers. Cambridge: Cambridge University Press.

    Book  Google Scholar 

  • Gemes, K. (1993). Hypothetico-deductivism: Content and the natural axiomatization of theories. Philosophy of Science, 60(3), 477–487.

    Article  Google Scholar 

  • Gemes, K. (1998). Hypothetico-deductivism: The current state of play; The criterion of empirical significance: Endgame. Erkenntnis, 49(1), 1–20.

    Article  Google Scholar 

  • Girard, J.-Y. (1987). Linear logic. Theoretical Computer Science, 50(1), 1–102.

    Article  Google Scholar 

  • Goodman, N. (1983). Facts, fiction and forecast (4th ed.). Cambridge: Harvard University Press.

    Google Scholar 

  • Grimes, T. R. (1990). Truth, content, and the hypothetico-deductive method. Philosophy of Science, 57(3), 514–522.

    Article  Google Scholar 

  • Hawthorne, J., & Fitelson, B. (2004). Discussion: Re-solving irrelevant conjunction with probabilistic independence. Philosophy of Science, 71(4), 505–514.

    Article  Google Scholar 

  • Hempel, C. G. (1943). A purely syntactical definition of confirmation. The Journal of Symbolic Logic, 8(4), 122–143.

    Article  Google Scholar 

  • Hempel, C. G. (1945a). Studies in the logic of confirmation I. Mind, 54(213), 1–26.

    Article  Google Scholar 

  • Hempel, C. G. (1945b). Studies in the logic of confirmation II. Mind, 54(214), 97–121.

    Article  Google Scholar 

  • Huber, F. (2008). Hempel’s logic of confirmation. Philosophical Studies, 139(2), 181–189.

    Article  Google Scholar 

  • Hughes, G. E., & Cresswell, M. J. (1996). A new introduction to modal logic. Abingdon: Routledge.

    Book  Google Scholar 

  • Hyland, M., & De Paiva, V. (1993). Full intuitionistic linear logic (extended abstract). Annals of Pure and Applied Logic, 64(3), 273–291.

    Article  Google Scholar 

  • Maher, P. (1999). Inductive logic and the ravens paradox. Philosophy of Science, 66(1), 50–70.

    Article  Google Scholar 

  • Maher, P. (2004). Probability captures the logic of scientific confirmation. In C. Hitchcock (Ed.), Contemporary Debates in Philosophy of Science (pp. 69–93). Blackwell Publishing Ltd.

  • Maher, P. (2005). Confirmation theory. In D. M. Borchert (Ed.), Encyclopedia of philosophy (2nd ed.). Basingstoke: Macmillan.

    Google Scholar 

  • Moretti, L. (2006). The tacking by disjunction paradox: Bayesianism versus hypothetico-deductivism. Erkenntnis, 64(1), 115–138.

    Article  Google Scholar 

  • Peterson, C. (2014a). Analyse de la structure logique des inférences légales et modélisation du discours juridique. Ph.D. thesis, Université de Montréal.

  • Peterson, C. (2014b). The categorical imperative: Category theory as a foundation for deontic logic. Journal of Applied Logic, 12(4), 417–461.

    Article  Google Scholar 

  • Peterson, C. (2014c). Monoidal logics: How to avoid paradoxes. In A. Lieto, D. P. Radicioni, M. Cruciani (Eds.), Proceedings of the international workshop on artificial intelligence and cognition (AIC 2014) (Vol. 1315, pp. 122–133). CEUR Workshop Proceedings.

  • Peterson, C. (2015). Contrary-to-duty reasoning: A categorical approach. Logica Universalis, 9(1), 47–92.

    Article  Google Scholar 

  • Peterson, C. (2016). A comparison between monoidal and substructural logics. Journal of Applied Non-Classical Logics, 26(2), 126–159.

    Article  Google Scholar 

  • Peterson, C., & Kulicki, P. (2016). Conditional normative reasoning with substructural logics: New paradoxes and De Morgan’s dualities. In O. Roy, A. Tamminga, & M. Willer (Eds.), Deontic logic and normative systems (pp. 220–236). London: College Publications.

    Google Scholar 

  • Schurz, G. (1991). Relevant deduction: From solving paradoxes towards a general theory. Erkenntnis, 35(1–3), 391–437.

    Google Scholar 

  • Sprenger, J. (2009). Hempel and the paradoxes of confirmation. In D. M. Gabbay, S. Hartmann, & J. Woods (Eds.), Handbook of the history of logic (Vol. 10, pp. 235–263). Amsterdam: Elsevier.

    Google Scholar 

  • Swinburne, R. G. (1971). The paradoxes of confirmation: A survey. American Philosophical Quarterly, 8(4), 318–330.

    Google Scholar 

  • Sylvan, R. & Nola, R. (1991). Confirmation without paradoxes. In G. Schurz & G. J. W. Dorn (Eds.), Advances in scientific philosophy: Essays in honour of Paul Weingartner on the occasion of the 60th anniversary of his birthday, Pozniań studies in the philosophy of the sciences and the humanities (Vol. 24, pp. 5–44). Amsterdam: Rodopi.

Download references

Acknowledgements

I am indebted to the comments and suggestions made by anonymous reviewers on previous drafts of this paper. I am also grateful to Stephan Hartmann as well as to the people of the Munich Center for Mathematical Philosophy, where I had the chance to work on that project. This work was financially supported by the Social Sciences and Humanities Research Council of Canada.

Author information

Authors and Affiliations

  1. Munich Center for Mathematical Philosophy, Ludwig-Maximilians-Universität München, Munich, Germany

    Clayton Peterson

Authors
  1. Clayton Peterson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Clayton Peterson.

Appendix

Appendix

Proposition 1

The equivalence between (RM) and (RE) + (M) requires the definition of aC.

Proof

First, (RE) trivially follows from (RM). Second, the derivation of (M) from (RM) requires the rules governing the introduction and the elimination of \(\otimes\).

figure x

Similarly, the derivation of (RM) from (RE) and (M) also requires these rules.

figure y

\(\square\)

Proposition 2

(RR) implies (C).

Proof

figure z

\(\square\)

Proposition 3

If \({\mathcal {D}}\) satisfies the definition of aC , then (RR) implies (RM).

Proof

First, note that a C satisfies (\(\Delta\)) and (F).

$$\begin{aligned} \varphi \longrightarrow \varphi \otimes \varphi \end{aligned}$$
(\Delta)
$$\begin{aligned} \varphi \otimes \varphi \longrightarrow \varphi \end{aligned}$$
(F)
figure aa

\(\square\)

Proposition 4

(RR) + (RE) + (M) implies (RM).

Proof

figure ab

\(\square\)

Proposition 5

(RM) + (C) implies (RR).

Proof

figure ac

\(\square\)

Lemma 1

Let \({\mathcal {D}}\)be a monotonic deductive system satisfying (D), then \(\Box 0 \longrightarrow 0\) is derivable.

Proof

figure ad

\(\square\)

Lemma 2

Given a SCC co S , \(0 \cong 0\otimes \lnot 0\).

Proof

figure ae

\(\square\)

Lemma 3

Given a SCC co S , \(\lnot 0\cong 1\).

Proof

figure af

\(\square\)

Lemma 4

Given a SCC co S , \(\varphi \longrightarrow \psi\)if and only if \(\lnot \psi \longrightarrow \lnot \varphi\).

Proof

Note that (b\(^-\)) is derivable (though the proof is left to the reader).Footnote 18

figure ag

\(\square\)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peterson, C. Studies in the logic of K-onfirmation. Philos Stud 176, 437–471 (2019). https://doi.org/10.1007/s11098-017-1023-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11098-017-1023-1

Keywords

Search

Navigation