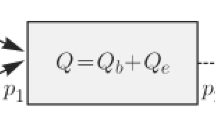Skip to main content
SpringerLink
Log in

On a mathematical theory of embolism

  • Published:
Acta Biotheoretica Aims and scope Submit manuscript

Abstract

A theory of embolism based on an optimization model of blood flow is proposed and used to explain the topographic distribution of emboli in arterial trees.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a:

initial segment of an artery prior to a bifurcation

b:

smaller of two branches at a bifurcation

p:

larger of two branches at a bifurcation

n:

an arbitrary bifurcation in a vascular hierarchy

r:

radius

Q:

flow rate

j:

exponent on Q, specific for type of steady flow

x:

optimal branch exponent (see text)

k:

optimal branch coefficient (see text)

S:

probability of an embolus flowing into an arterial segment

a,b,c,...:

constants; coefficients on variables

References

  • Altman, J.S. and D.S. Dittmer (1972). Respiration and Circulation. Federation of American Societies of Experimental Biology.

  • Griffith, T.M., D.H. Edwards, R.L. Davies and A.H. Henderson (1989). The role of EDRF in flow distribution: A microangiographic study of the rabbit isolated ear. Microvas. Res. 37: 162–177.

    Google Scholar 

  • McDonald, D.A. (1960). Blood Flow in Arteries. London, Arnold Ltd.

    Google Scholar 

  • Murray, C.D. (1926). The physiological principle of minimum work. I. The vascular system and the cost of blood volume. Proc Natl Acad. Sci. USA 12: 207–214.

    Google Scholar 

  • Pollanen, M.S. and J.H.N. Deck (1989). Directed embolization is an alternate cause of watershed infarction. Arch. Pathol. Lab. Med. 113: 1139–1141.

    Google Scholar 

  • Pollanen, M.S. and J.H.N. Deck(1990). The mechanism of embolic watershed infarction; Experimental studies. Can. J. Neurol. Sci. 17: 395–398.

    Google Scholar 

  • Pollanen, M.S. (1991a). Behaviour of suspended particles at bifurcation: Implications for embolism. Phys. Med. Biol. 36: 397–401.

    Google Scholar 

  • Pollanen, M.S. (1991b). A Hempelian explanatory shift in neuropathology: A study in the history and logic of medicine. Can. Bull. Med. Hist. 8: 65–67.

    Google Scholar 

  • Pollanen, M.S. (1992). Dimensional optimization at different levels of the arterial hierarchy. J. theor. Biol. 159: 267–270.

    Google Scholar 

  • Sherman, T.F. (1981). On connecting large to small: The meaning of Murray's law. J. Gen. Physiol. 78: 431–453.

    Google Scholar 

  • Stein, P.D. and H.N. Sabbah (1976). Turbulent blood flow in the ascending aorta of humans with normal and diseased aortic valves. Circ. Res. 39: 58–65.

    Google Scholar 

  • Torvik, A. and K. Skullerud (1982). Watershed infarcts in the brain caused by microemboli. Clin. Neuropathol. 1: 99–195.

    Google Scholar 

  • Uylings, H.B.M. (1977). Optimization of diameters and bifurcation angles in lung and vascular tree structures. Bull. Math. Biol. 39: 509–520.

    Google Scholar 

  • Zamir, M. (1988a). The branching structure of arterial trees. Comment Theor. Biol. 1: 15–37.

    Google Scholar 

  • Zamir, M. (1988b). Distributing and delivering vessels of the human heart. J. Gen. Physiol. 91: 725–735.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Pathology, Division of Neuropathology, University of Toronto, Ontario, Canada

    Michael S. Pollanen

Authors
  1. Michael S. Pollanen
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pollanen, M.S. On a mathematical theory of embolism. Acta Biotheor 41, 191–197 (1993). https://doi.org/10.1007/BF00712166

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00712166

Key words

Search

Navigation