Abstract
Modern belief revision theory is based to a large extent on partial meet contraction that was introduced in the seminal article by Carlos Alchourrón, Peter Gärdenfors, and David Makinson that appeared in 1985. In the same year, Alchourrón and Makinson published a significantly different approach to the same problem, called safe contraction. Since then, safe contraction has received much less attention than partial meet contraction. The present paper summarizes the current state of knowledge on safe contraction, provides some new results and offers a list of unsolved problems that are in need of investigation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The quote is taken from Carnota and Rodríguez (2011, p. 8). According to Google Scholar, in December 2012 the AGM paper on partial meet contraction had been quoted thirteen times more often than Alchourrón and Makinson’s paper on safe contraction.
- 2.
Thus \(X \in K \bot \phi \) if and only if (1) \(X \subseteq K\), (2) \(X \nvdash \phi \), and (3) \(X' \vdash \phi \) whenever \(X \subset X' \subseteq K\). It is easy to check that a \(\phi \)-remainder of \(K\) is logically closed if \(K\) is.
- 3.
Thus \(X \in K \perp \!\!\!\perp \phi \) if and only if (1) \(X \subseteq K\), (2) \(X \vdash \phi \), and (3) \(X' \nvdash \phi \) whenever \(X' \subset X\). Kernels, and in particular consistent kernels, have played an important role in a certain brand of argumentation theory, see the definition of an “argument” and of a “contour” in Besnard and Hunter (2008, pp. 39, 176) . Besnard and Hunter’s theory, however, does not use any orderings of certainty, reliability or priority over the sentences of the language.
- 4.
Thus the sentences not included in any \(\phi \)-kernel are safe with respect to \(\phi \). They correspond to the full meet contraction by \(\phi \).
- 5.
Here we tacitly assume that logically equivalent sentences are interchangeable. See Sect. 2 for a more precise definition. For sets of sentences \(H\) that are not logically closed, Alchourrón and Makinson define safe contraction as
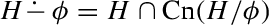 .
. - 6.
Compare the comments by Alchourrón and Makinson (1986), Sect. 2.1, on “Dominance and Maximality”, and by Sen (1997, Sect. 5) on “Maximization and Optimization”. For a short discussion of the advantages of using strict relations, cf. Rott (1992b, pp. 50–52). The non-strict AGM relations \(\sqsubseteq \) are, more correctly speaking, of the “less-than-or-equal-to-or-incomparable-with” type.
- 7.
- 8.
Acyclicity is also known as non-circularity.
- 9.
Cf. Rott (1993, p. 1438).
- 10.
Cf. Sen (1986, p. 1097).
- 11.
See Rott (2001, especially p. 104).
- 12.
Makinson (1989, p. 16) finitistic “loop condition” for non-monotonic reasoning is similar in spirit to (K
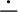 Trans) and (K
Trans) and (K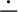 Acyc). Translated into the language of contractions, it reads thus: If for all \(i \in \{i_1,\dots i_{n-1}\}\),
Acyc). Translated into the language of contractions, it reads thus: If for all \(i \in \{i_1,\dots i_{n-1}\}\), 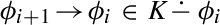 and furthermore
and furthermore 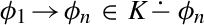 , then
, then 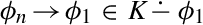 .
. - 13.
For a similar example, compare Rott (2003, p. 268, see Footnote 20).
- 14.
If \(\prec \) satisfies Intersubstitutivity and Choice, then (EII\(^-\)) is equivalent with the following property: If \(\phi \wedge \psi \prec \chi \) and \(\nvdash \chi \), then there are \(\xi \) and \(\rho \) such that \(\chi \dashv \vdash \xi \wedge \rho \) and \(\phi \wedge \rho \prec \xi \) and \(\psi \wedge \xi \prec \rho \). Notice that given (CH), this condition, as well as (EII\(^-\)) itself, is a transcription of the contraction postulate (K
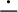 8r\('\)) into the language of entrenchments.
8r\('\)) into the language of entrenchments. - 15.
See Rott (2001), Lemma 52 (viii).
- 16.
For the formulation in terms of strict preference relations, compare Alchourrón and Makinson (1986, Sect. 2.1).
- 17.
The acyclicity of relations involved in relational partial meet contractions is guaranteed by the requirement that choice functions select a non-empty choice set whenever the menu is non-empty.
- 18.
For the formulation in terms of strict preference relations, please compare Rott (1993, p. 1430, and in particular Footnote 1).
- 19.
Compare Footnote 6 and the surrounding text.
- 20.
It can be shown that negative entrenchment is a refinement of positive entrenchment. Negative entrenchment introduces new distinctions within levels of positive entrenchment. While all beliefs are comparable in terms of the less discriminating positive entrenchment relation, negative entrenchment introduces incomparabilities. For this, see Rott (2000).
- 21.
Recall that Continuing up and Continuing down jointly imply Intersubstitutivity.
- 22.
Suppose that Virtual connectivity is given and (EII) is violated. Concerning the latter, suppose that \(\phi \wedge \psi < \chi \) and \(\phi \not < \chi \) and \(\psi \not < \chi \). Then by Virtual connectivity, \(\phi \wedge \psi < \phi \) and \(\phi \wedge \psi < \psi \). Then by the right-to-left direction of Choice, \(\psi < \phi \) and \(\phi < \psi \), contradicting Asymmetry.
- 23.
Another way to achieve a similar result is to apply partial meet contraction primarily to the inconsistent belief set, i.e., the whole language, and then define contraction on consistent sets as restrictions in the following way:
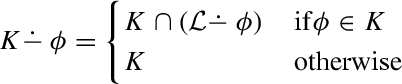
This idea was briefly discussed for entrenchment-based contractions in Rott (1992b, Sect. 7) and more thoroughly analyzed for all AGM contraction models by Areces and Becher (2001).
- 24.
This applies to belief sets. As was shown in Hansson (1993), for belief bases it is a non-empty condition. A global partial meet contraction on belief bases is unified if and only if it satisfies:
If \(\phi \notin \mathrm {Cn}(\varnothing )\) and each element of \(Z\) implies \(\phi \), then
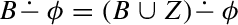 (Redundancy).
(Redundancy). - 25.
This also holds for belief bases.
- 26.
Thus \(X \in K \perp \!\!\!\perp A\) if and only if (1) \(X \subseteq K\), (2) \(X \vdash _\exists A\), and (3) \(X' \nvdash _\exists A\) for all \(X' \subset X\).
- 27.
Thus \(X \in K \veebar A\) if and only if (1) \(X \subseteq K\), (2) \(A \subseteq \mathrm {Cn}(X)\), and (3) \(A \nsubseteq \mathrm {Cn}(X')\) for all \(X' \subset X\).
- 28.
We would like to dedicate this paper to David Makinson, whom we admire as a researcher and who has been, in many and various ways, a long-term friend and mentor to both of us. Thank you so much, David! Our paper is the outcome of a truly joint undertaking. However, unless otherwise indicated, the results reported in Sects. 3 and 4 are Hans Rott’s and the results reported in Sects. 5, 6 and 7 are Sven Ove Hansson’s. We are grateful to Eduardo Fermé, David Makinson and in particular Richard Booth for very helpful comments on an earlier version of this paper.
- 29.
Those who are worried about the fact that the contraction function operates over the absurd belief set \(K_\bot \) may want to modify the example by introducing a third atom \(r\), replacing \(K_\bot \) by \(\mathrm {Cn}(r)\) and replacing
 by
by 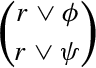 .
. - 30.
Compare Rott (2001, Observation 64).
References
Alchourrón, C., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. Journal of Symbolic Logic, 50, 510–530.
Alchourrón, C. E., & Makinson, D. (1985). On the logic of theory change: Safe contraction. Studia Logica, 44, 405–422.
Alchourrón, C. E., & Makinson, D. (1986). Maps between some different kinds of contraction function: The finite case. Studia Logica, 45, 187–198.
Areces, C., & Becher, V. (2001). Iterable AGM functions. In M.-A. Williams & H. Rott (Eds.), Frontiers in Belief Revision (pp. 261–277). Dordrecht: Kluwer.
Besnard, P., & Hunter, A. (2008). Elements of Argumentation. Cambridge, MA: MIT Press.
Carnota, R., & Rodríguez, R. (2011). AGM theory and artificial intelligence. In E. J. Olsson & S. Enqvist (Eds.), Belief Revision meets Philosophy of Science (pp. 1–42). Dordrecht: Springer.
Falappa, M., Fermé, E., & Kern-Isberner, G. (2006). On the Logic of Theory Change: Relations Between Incision and Selection Functions. In G. Brewka et al. (eds.), ECAI’2006, 17th European Conference on Artificial Intelligence (pp. 402–406). IOS Press.
Fermé, E., & Hansson, S. O. (2011). AGM 25 years of research in belief change. Journal of Philosophical Logic, 40, 295–331.
Fermé, E., & Reis, M. (2012). System of spheres-based multiple contractions. Journal of Philosophical Logic, 41, 29–52.
Fermé, E., Saez, K., & Sanz, P. (2003). Multiple kernel contraction. Studia Logica, 73, 183–195.
Fuhrmann, A., & Hansson, S. O. (1994). A survey of multiple contractions. Journal of Logic, Language, and Information, 3, 39–76.
Gärdenfors, P. (1982). Rules for rational changes of belief. In T. Pauli (Ed.), \(\langle \)320311\(\rangle \): Philosophical Essays Dedicated to Lennart Åqvist on His Fiftieth Birthday, Vol. 34 (pp. 88–101). Uppsala: University of Uppsala Philosophical Studies.
Gärdenfors, P. (1988). Knowledge in flux: Modeling the dynamics of epistemic states. Cambridge, MA: Bradford Books, MIT Press.
Gärdenfors, P., & Makinson, D. (1988). Revisions of knowledge systems using epistemic entrenchment. In M. Vardi (Ed.), TARK’88: Proceedings of the Second Conference on Theoretical Aspects of Reasoning About Knowledge (pp. 83–95). Los Altos, CA: Morgan Kaufmann.
Hansson, S. O. (1989). New operators for theory change. Theoria, 55, 114–132.
Hansson, S. O. (1992). A dyadic representation of belief. In P. Gärdenfors (Ed.), Belief Revision (pp. 89–121). Cambridge: Cambridge University Press.
Hansson, S. O. (1993). Reversing the Levi identity. Journal of Philosophical Logic, 22, 637–669.
Hansson, S. O. (1994). Kernel contraction. Journal of Symbolic Logic, 59, 845–859.
Hansson, S. O. (1999a). A Textbook of Belief Dynamics. Theory Change and Database Updating. Dordrecht : Kluwer.
Hansson, S. O. (1999b). A survey of non-prioritized belief revision. Erkenntnis, 50, 413–427.
Hansson, S. O. (2010). Multiple and iterated contraction reduced to single-step single-sentence contraction. Synthese, 173, 153–177.
Hansson, S. O. (2012). Global and iterated contraction and revision: An exploration of uniform and semi-uniform approaches. Journal of Philosophical Logic, 41, 143–172.
Hansson, S. O., Fermé, E., Cantwell, J., & Falappa, M. (2001). Credibility-limited revision. Journal of Symbolic Logic, 66, 1581–1596.
Li, J. (1998). A note on partial meet package contraction. Journal of Logic, Language and Information, 7, 139–142.
Makinson, D. (1987). On the status of the postulate of recovery in the logic of theory change. Journal of Philosophical Logic, 16, 383–394.
Makinson, D. (1989). General theory of cumulative inference. In M. Reinfrank, J. de Kleer, M. Ginsberg, & E. Sandewall (Eds.), Non-Monotonic Reasoning—Proceedings of the 2nd International Workshop Grassau, FRG, June 13–15, 1988 (pp. 1–18). Berlin: Springer.
Makinson, D. (1997). Screened revision. Theoria, 63, 14–23.
Reis, M., & Fermé, E. (2012). Possible worlds semantics for partial meet multiple contraction. Journal of Philosophical Logic, 41, 7–28.
Rott, H. (1992a). On the logic of theory change: More maps between different kinds of contraction functions. In P. Gärdenfors (Ed.), Belief Revision (pp. 122–141). Cambridge: Cambridge University Press.
Rott, H. (1992b). Preferential belief change using generalized epistemic entrenchment. Journal of Logic, Language and Information, 1, 45–78.
Rott, H. (1993). Belief contraction in the context of the general theory of rational choice. Journal of Symbolic Logic, 58, 1426–1450.
Rott, H. (1999). Coherence and conservatism in the dynamics of belief. Part I: Finding the right framework. Erkenntnis, 50, 387-412.
Rott, H. (2000). Just because: Taking belief bases seriously. In S. R. Buss, P. Hájek, & P. Pudlák (Eds.), Logic Colloquium ’98—Proceedings of the Annual European Summer Meeting of the Association for Symbolic Logic held in Prague, Urbana (pp. 387–408). Urbana, Ill: Association for Symbolic Logic.
Rott, H. (2001). Change, choice and inference: A study of belief revision and nonmonotonic reasoning. Oxford: Oxford University Press.
Rott, H. (2003). Basic entrenchment. Studia Logica, 73, 257–280.
Sen, A. (1986). Social choice theory. In K. J. Arrow & M. D. Intriligator (Eds.), Handbook of Mathematical Economics (Vol. III, pp. 1073–1181). Amsterdam: Elsevier/North-Holland.
Sen, A. (1997). Maximization and the act of choice. Econometrica, 65, 745–779.
Spohn, W. (2010) Multiple contraction revisited. In M. Suárez, M. Dorato & M. Rédei (Eds.), EPSA Epistemology and Methodology of Science. Launch of the European Philosophy of Science Association, (Vol. 1, pp. 279–288). Dordrecht: Springer.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Proofs
Appendix: Proofs
Proof of Theorem 1. It was shown by Alchourrón, Gärdenfors and Makinson (1985, Observation 3.3) that (K 7) and (K
7) and (K 7P) are equivalent, and by Rott (1992b, Lemma 2) that (K
7P) are equivalent, and by Rott (1992b, Lemma 2) that (K 7) and (K
7) and (K 7p) are equivalent. QED
7p) are equivalent. QED
Proof of Theorem 2. (i) (K 8r) implies (K
8r) implies (K 8r\('\)): By (K
8r\('\)): By (K 6) and (K
6) and (K 8r), we get that
8r), we get that  . Now let
. Now let  . Thus, by the compactness of \(\mathrm {Cn}\), we have finite sets
. Thus, by the compactness of \(\mathrm {Cn}\), we have finite sets  and
and  such that \(M\cup N \vdash \chi \). Now define \(\xi \) to be \((\bigwedge M)\vee \chi \) and \(\rho \) to be \((\bigwedge N)\vee \chi \). By (K
such that \(M\cup N \vdash \chi \). Now define \(\xi \) to be \((\bigwedge M)\vee \chi \) and \(\rho \) to be \((\bigwedge N)\vee \chi \). By (K 1), \(\xi \) is in
1), \(\xi \) is in  and \(\rho \) is in
and \(\rho \) is in  . Furthermore, we have \(\chi \dashv \vdash \xi \wedge \rho \), as required by (K
. Furthermore, we have \(\chi \dashv \vdash \xi \wedge \rho \), as required by (K 8r\('\)).
8r\('\)).
(K 8r\('\)) implies (K
8r\('\)) implies (K 8r): Let
8r): Let  . By (K
. By (K 2), \(\chi \in K\), so by (K
2), \(\chi \in K\), so by (K 5) and (K
5) and (K 1),
1),  and
and  . Thus
. Thus  contains \(\lnot (\phi \vee \psi )\vee \chi \). In order to show that it contains \(\chi \), it is thus sufficient to show that it also contains \(\phi \vee \psi \vee \chi \). By (K
contains \(\lnot (\phi \vee \psi )\vee \chi \). In order to show that it contains \(\chi \), it is thus sufficient to show that it also contains \(\phi \vee \psi \vee \chi \). By (K 1),
1),  , and by (K
, and by (K 6),
6),  . Now we are ready to apply (K
. Now we are ready to apply (K 8r\('\)) and get that there are \(\xi \) and \(\rho \) such that \((\phi \vee \psi \vee \chi ) \dashv \vdash \xi \wedge \rho \) and
8r\('\)) and get that there are \(\xi \) and \(\rho \) such that \((\phi \vee \psi \vee \chi ) \dashv \vdash \xi \wedge \rho \) and  and
and  . That is, by (K
. That is, by (K 1),
1),  and
and  . Hence,
. Hence,  and, finally,
and, finally,  , as desired.
, as desired.
(ii) (K 8wd) implies (K
8wd) implies (K 8p): Let
8p): Let  . Then by (K
. Then by (K 8wd),
8wd),  or
or  , which simplifies to
, which simplifies to  or
or  .
.
(K 8p) implies (K
8p) implies (K 8wd): Let
8wd): Let  . Then by (K
. Then by (K 1) and (K
1) and (K 6)
6)  . Thus by (K
. Thus by (K 8p)
8p)  or
or  . Which reduces by (K
. Which reduces by (K 6) to
6) to  or
or  . By (K
. By (K 2) and (K
2) and (K 5),
5),  and
and  . By (K
. By (K 1), it follows that
1), it follows that  or
or  .
.
(iii) For the non-obvious direction, suppose to the contrary that (K 8d) holds but not (K
8d) holds but not (K 8d\('\)). Since (K
8d\('\)). Since (K 8d\('\)) does not hold there are \(\alpha \), \(\beta \), \(\phi \), and \(\psi \) such that
8d\('\)) does not hold there are \(\alpha \), \(\beta \), \(\phi \), and \(\psi \) such that  ,
,  ,
,  , and
, and  . It follows from (K
. It follows from (K 1) that
1) that  ,
,  , and
, and  , contrary to (K
, contrary to (K 8d).
8d).
(iv) Suppose that  . We want to show that either
. We want to show that either  or
or  . By (K
. By (K 1),
1),  , and by (K
, and by (K 6),
6),  . So by (K
. So by (K 8p) which we already proved to be relatively equivalent with (K
8p) which we already proved to be relatively equivalent with (K 8wd), either
8wd), either  or
or  . By (K
. By (K 8c), this reduces to either
8c), this reduces to either  or
or  . Using (K
. Using (K 1), we get that either
1), we get that either  or
or  . But by (K
. But by (K 2) and (K
2) and (K 5), both
5), both  and
and  . So by (K
. So by (K 1) again, either
1) again, either  or
or  , as desired.
, as desired.
(v) Figure 3 depicts a contraction function over \(K=K_\bot \) that satisfies (K 1) – (K
1) – (K 7), (K
7), (K 8c) and (K
8c) and (K 8r), but not (K
8r), but not (K 8wd). This contraction function derives from the (vacuously transitive) partial ordering \(\leftarrow \) between the four possible worlds \(pq\), \(p\overline{q}\), \(\overline{p}q\) and \(\overline{p}\overline{q}\) that is fully specified by \(pq \leftarrow \overline{p}\overline{q}\) and \(p\overline{q} \leftarrow \overline{p}q\) (where the arrows point to the “more plausible” worlds). Having Grovean semantics for AGM in mind, it can be recognized as a partial meet contraction based on a transitive strict preference relation, and thus Theorem 14 (ii) applies (a similar example is given in Rott 2001, p. 164).Footnote 29 The violation of (K
8wd). This contraction function derives from the (vacuously transitive) partial ordering \(\leftarrow \) between the four possible worlds \(pq\), \(p\overline{q}\), \(\overline{p}q\) and \(\overline{p}\overline{q}\) that is fully specified by \(pq \leftarrow \overline{p}\overline{q}\) and \(p\overline{q} \leftarrow \overline{p}q\) (where the arrows point to the “more plausible” worlds). Having Grovean semantics for AGM in mind, it can be recognized as a partial meet contraction based on a transitive strict preference relation, and thus Theorem 14 (ii) applies (a similar example is given in Rott 2001, p. 164).Footnote 29 The violation of (K 8wd) is this: We have
8wd) is this: We have  but neither
but neither  nor
nor  . QED
. QED
Proof of Theorem 3. (i) To prove (K Acyc), suppose for reductio that
Acyc), suppose for reductio that  and \(\nvdash \phi _i\wedge \phi _{i+1}\) for all \(i=1\), ..., \(n-\)1, and that
and \(\nvdash \phi _i\wedge \phi _{i+1}\) for all \(i=1\), ..., \(n-\)1, and that  and \(\nvdash \phi _n\wedge \phi _1\). By (K
and \(\nvdash \phi _n\wedge \phi _1\). By (K 7p) which is equivalent with (K
7p) which is equivalent with (K 7), it follows that
7), it follows that  for all \(i=1,\dots ,n-1\), and
for all \(i=1,\dots ,n-1\), and  . Thus, by (K
. Thus, by (K 1),
1),  . But since clearly \(\nvdash \phi _1\wedge \dots \wedge \phi _n\), this contradicts (K
. But since clearly \(\nvdash \phi _1\wedge \dots \wedge \phi _n\), this contradicts (K 4).
4).
(ii) To prove (K Trans), we assume that
Trans), we assume that  , \(\nvdash \phi \wedge \psi \),
, \(\nvdash \phi \wedge \psi \),  , and \(\nvdash \psi \wedge \chi \). Applying (K
, and \(\nvdash \psi \wedge \chi \). Applying (K 7p) and (K
7p) and (K 6) to
6) to  we obtain
we obtain  , to which we apply (K
, to which we apply (K 8c) and (K
8c) and (K 6) to obtain
6) to obtain  . We also have
. We also have  which with (K
which with (K 7p) and (K
7p) and (K 6) yields
6) yields  . We can finally combine this with
. We can finally combine this with  and obtain
and obtain  as desired. It remains to be shown that \(\not \vdash \phi \wedge \chi \). Suppose for reductio that \(\vdash \phi \wedge \chi \). Then we can conclude from \(\vdash \phi \) and (K
as desired. It remains to be shown that \(\not \vdash \phi \wedge \chi \). Suppose for reductio that \(\vdash \phi \wedge \chi \). Then we can conclude from \(\vdash \phi \) and (K 6) that
6) that  . In combination with the assumption
. In combination with the assumption  this yields
this yields  . Then (K
. Then (K 4) yields \(\vdash \psi \). Thus \(\vdash \phi \wedge \psi \), contradicting one of our assumptions. QED
4) yields \(\vdash \psi \). Thus \(\vdash \phi \wedge \psi \), contradicting one of our assumptions. QED
Proof of Theorem 6. We give an example of a contraction function satisfying (K 1) – (K
1) – (K 6) that cannot be represented as a safe contraction. Consider the language \(\mathcal {L}\) that has only two propositional variables, \(p\) and \(q\). Let \(K= \mathrm {Cn}(\{p,q\})\). Consider now a basic AGM contraction function with the following values:
6) that cannot be represented as a safe contraction. Consider the language \(\mathcal {L}\) that has only two propositional variables, \(p\) and \(q\). Let \(K= \mathrm {Cn}(\{p,q\})\). Consider now a basic AGM contraction function with the following values:

There is nothing in (K 1) – (K
1) – (K 6) that prevents a contraction function from having these values. The values for other sentences are irrelevant. We now show that such a function cannot be generated through safe contraction.
6) that prevents a contraction function from having these values. The values for other sentences are irrelevant. We now show that such a function cannot be generated through safe contraction.
Consider first  . Besides the singleton \(p\)-kernels \(\{p\wedge q\}\) and \(\{p\}\), there are four \(p\)-kernels of \(K\) (modulo logical equivalence), viz.,
. Besides the singleton \(p\)-kernels \(\{p\wedge q\}\) and \(\{p\}\), there are four \(p\)-kernels of \(K\) (modulo logical equivalence), viz.,
Suppose that the contraction function is a safe contraction associated with a hierarchy \(\prec \). Notice that \(\lnot p\vee q\), being a consequence of \(\lnot p\), is \(\prec \)-safe with respect to \(p\) anyway. Notice also that since  , \(p\vee \lnot q\) and \(p\leftrightarrow q\) must not be \(\prec \)-safe with respect to \(p\). Since
, \(p\vee \lnot q\) and \(p\leftrightarrow q\) must not be \(\prec \)-safe with respect to \(p\). Since  , either \(p\vee q\) or \(q\) itself has to be \(\prec \)-safe with respect to \(p\). Inspecting the four kernels, we realize that this means that
, either \(p\vee q\) or \(q\) itself has to be \(\prec \)-safe with respect to \(p\). Inspecting the four kernels, we realize that this means that
Second, we consider  . By exactly the same argument that we have just applied, we get that
. By exactly the same argument that we have just applied, we get that
Third, we consider  . Applying the same argument a third time, we get that
. Applying the same argument a third time, we get that
Assume, for the first part, that (A1) is true. Then, by the asymmetry of \(\prec \), (B2) cannot be true. So (B1) is true. But then, again by the asymmetry of \(\prec \), (C2) cannot be true. So (C1) is true as well. But from (A1), (B1) and (C1), we get the cycle
So assume for the first part that (A2) is true. Then, by the asymmetry of \(\prec \), (C1) cannot be true. So (C2) is true. But then, again by the asymmetry of \(\prec \), (B1) cannot be true. So (B2) is true. But from (A2), (C2) and (B2), we get the cycle
So either way, we have found a cycle, which is forbidden by the assumption that \(\prec \) is a hierarchy. We have found a contradiction and proved that  cannot be a safe contraction associated with \(\prec \). QED
cannot be a safe contraction associated with \(\prec \). QED
Proof of Theorem 8. That  satisfies (K
satisfies (K 7) is proven in Observation 5.3 of Alchourrón and Makinson (1985). It remains to verify (K
7) is proven in Observation 5.3 of Alchourrón and Makinson (1985). It remains to verify (K 8r). Let \(\chi \) be in
8r). Let \(\chi \) be in  . That is, there is a set \(M\) of \(\phi \wedge \psi \)-safe elements such that \(M\vdash \chi \). In order to show that \(\chi \) is in
. That is, there is a set \(M\) of \(\phi \wedge \psi \)-safe elements such that \(M\vdash \chi \). In order to show that \(\chi \) is in  , it suffices to show that there are sets \(N_1\) of \(\phi \)-safe and \(N_2\) of \(\psi \)-safe elements such that \(N_1 \cup N_2 \vdash \chi \). But since \(\prec \) continues down \(\vdash \) over \(K\), each \(\phi \wedge \psi \)-safe element is either \(\phi \)-safe or \(\psi \)-safe, by Corollary 5.4 of Alchourrón and Makinson (1985). So \(M\) can easily be split up into sets \(N_1\) and \(N_2\) as desired. QED
, it suffices to show that there are sets \(N_1\) of \(\phi \)-safe and \(N_2\) of \(\psi \)-safe elements such that \(N_1 \cup N_2 \vdash \chi \). But since \(\prec \) continues down \(\vdash \) over \(K\), each \(\phi \wedge \psi \)-safe element is either \(\phi \)-safe or \(\psi \)-safe, by Corollary 5.4 of Alchourrón and Makinson (1985). So \(M\) can easily be split up into sets \(N_1\) and \(N_2\) as desired. QED
Proof of Theorem 9. That  satisfies (K
satisfies (K 7) is proven in Observation 4.3 of Alchourrón and Makinson (1985). It remains to verify (K
7) is proven in Observation 4.3 of Alchourrón and Makinson (1985). It remains to verify (K 8c). Let \(\psi \) and \(\chi \) be in
8c). Let \(\psi \) and \(\chi \) be in  . That is, there are sets \(M\) and \(N\) of \(\phi \wedge \psi \)-safe elements such that \(M\vdash \psi \) and \(N\vdash \chi \). Let \(M\) and \(N\) be chosen minimal, so that they are finite, by compactness. We want to show that \(\chi \) is in
. That is, there are sets \(M\) and \(N\) of \(\phi \wedge \psi \)-safe elements such that \(M\vdash \psi \) and \(N\vdash \chi \). Let \(M\) and \(N\) be chosen minimal, so that they are finite, by compactness. We want to show that \(\chi \) is in  as well, that is, that there is a set \(P\) of \(\phi \)-safe elements such that \(P\vdash \chi \). Put \(P=N\). Now suppose that there is a set \(R\) such that \(R \vdash _{min} \phi \). By compactness, \(R\) is finite. Let \(\xi \in N\) be in \(R\). We need to show that there is a \(\rho \) in \(R\) such that \(\rho \prec \xi \). Clearly, \(M\cup R \vdash \phi \wedge \psi \). Define \(M' = \{(\bigwedge R) \!\rightarrow \!\sigma : \sigma \in M\}\). Then clearly, \(M'\cup R \vdash \phi \wedge \psi \). Since the elements of \(M\) are \(\phi \wedge \psi \)-safe and \(\prec \) continues up \(\vdash \) over \(K\), the elements of \(M'\) are \(\phi \wedge \psi \)-safe as well, by Lemma 4.1 of Alchourrón and Makinson (1985). Take a subset \(S\) of \(M'\cup R\) that minimally implies \(\phi \wedge \psi \). Notice that \(R\subseteq S\), because if some \(\alpha \) from \(R\) were missing from \(S\), then \(S\) could not imply \(\psi \). For suppose that \((R-\{\alpha \})\cup M' \vdash \phi \wedge \psi \). Then, since \(\lnot \phi \) is logically stronger than \(\lnot \bigwedge R\) and thus than \(M'\), we get that \((R-\{\alpha \})\cup \{\lnot \phi \} \vdash \phi \wedge \psi \), and thus \(R-\{\alpha \} \vdash \phi \), contradicting the minimality of \(R\).
as well, that is, that there is a set \(P\) of \(\phi \)-safe elements such that \(P\vdash \chi \). Put \(P=N\). Now suppose that there is a set \(R\) such that \(R \vdash _{min} \phi \). By compactness, \(R\) is finite. Let \(\xi \in N\) be in \(R\). We need to show that there is a \(\rho \) in \(R\) such that \(\rho \prec \xi \). Clearly, \(M\cup R \vdash \phi \wedge \psi \). Define \(M' = \{(\bigwedge R) \!\rightarrow \!\sigma : \sigma \in M\}\). Then clearly, \(M'\cup R \vdash \phi \wedge \psi \). Since the elements of \(M\) are \(\phi \wedge \psi \)-safe and \(\prec \) continues up \(\vdash \) over \(K\), the elements of \(M'\) are \(\phi \wedge \psi \)-safe as well, by Lemma 4.1 of Alchourrón and Makinson (1985). Take a subset \(S\) of \(M'\cup R\) that minimally implies \(\phi \wedge \psi \). Notice that \(R\subseteq S\), because if some \(\alpha \) from \(R\) were missing from \(S\), then \(S\) could not imply \(\psi \). For suppose that \((R-\{\alpha \})\cup M' \vdash \phi \wedge \psi \). Then, since \(\lnot \phi \) is logically stronger than \(\lnot \bigwedge R\) and thus than \(M'\), we get that \((R-\{\alpha \})\cup \{\lnot \phi \} \vdash \phi \wedge \psi \), and thus \(R-\{\alpha \} \vdash \phi \), contradicting the minimality of \(R\).
Now since \(S \vdash _{min} \phi \wedge \psi \), we can apply the fact that \(\xi \in N\) is \(\phi \wedge \psi \)-safe and conclude that there is a \(\rho ^0\) in \(S\) such that \(\rho ^0 \prec \xi \). Now this \(\rho ^0\) is either in \(R\) or in \(M'\). But if it is in \(M'\), we can, by the fact that the elements of \(M'\) are \(\phi \wedge \psi \)-safe, find another sentence \(\rho ^1\) with \(\rho ^1\prec \rho ^0\) which again is either in \(R\) or in \(M'\). If \(\rho ^1\) is in \(M'\), we repeat the process again, and so on. Since \(M'\) is finite and \(\prec \) is acyclic and transitive, there must finally be a \(\rho ^n\) with \(\rho ^n\prec \xi \) which is not in \(M'\) but in \(R\). This is the \(\rho \) we have been looking for. QED
Proof of Lemma 10. In the presence of the basic AGM postulates including (K 4), Definition 4 above is equivalent to Definition 17 of Rott (2001, p. 229). Thus, the hierarchies obtained by (CH) are relations of epistemic entrenchment. With the exception of (v) and (vi), the claims of Lemma 10 are all listed in part (ii) of Observation 68 of Rott (2001, p. 263), although (viii) is a slightly strengthened form for the present context. (v) is trivial. We prove (vi). Suppose that \(\phi \wedge \psi \prec \chi \) and \(\nvdash \chi \). This means, by (CH), that
4), Definition 4 above is equivalent to Definition 17 of Rott (2001, p. 229). Thus, the hierarchies obtained by (CH) are relations of epistemic entrenchment. With the exception of (v) and (vi), the claims of Lemma 10 are all listed in part (ii) of Observation 68 of Rott (2001, p. 263), although (viii) is a slightly strengthened form for the present context. (v) is trivial. We prove (vi). Suppose that \(\phi \wedge \psi \prec \chi \) and \(\nvdash \chi \). This means, by (CH), that  and \(\nvdash \phi \wedge \psi \). By (K
and \(\nvdash \phi \wedge \psi \). By (K 8r), it follows that
8r), it follows that  . By the compactness of \(\mathrm {Cn}\), there are finite sets
. By the compactness of \(\mathrm {Cn}\), there are finite sets  and
and  such that \(M\cup N \vdash \chi \). By (K
such that \(M\cup N \vdash \chi \). By (K 1), we have
1), we have  ,
,  and \(\chi \dashv \vdash ((\bigwedge M) \vee \chi ) \wedge ((\bigwedge N) \vee \chi )\). Let \(\xi \) be \((\bigwedge M) \vee \chi \) and \(\rho \) be \((\bigwedge N) \vee \chi \). Since both \(\xi \) and \(\rho \) are in \(\mathrm {Cn}(\chi )\), we have, by (K
and \(\chi \dashv \vdash ((\bigwedge M) \vee \chi ) \wedge ((\bigwedge N) \vee \chi )\). Let \(\xi \) be \((\bigwedge M) \vee \chi \) and \(\rho \) be \((\bigwedge N) \vee \chi \). Since both \(\xi \) and \(\rho \) are in \(\mathrm {Cn}(\chi )\), we have, by (K 6),
6),  and
and  . Thus, since \(\nvdash \phi \wedge \chi \) and \(\nvdash \psi \wedge \chi \), \(\phi \wedge \chi \prec \xi \) and \(\psi \wedge \chi \prec \rho \), as desired. QED
. Thus, since \(\nvdash \phi \wedge \chi \) and \(\nvdash \psi \wedge \chi \), \(\phi \wedge \chi \prec \xi \) and \(\psi \wedge \chi \prec \rho \), as desired. QED
Proof of Theorem 11. The hierarchy \(\prec \) defined by (CH) can be used to reconstruct the given contraction function  as a safe contraction, provided that
as a safe contraction, provided that  has the properties mentioned. The properties of \(\prec \) are listed in Lemma 10.
has the properties mentioned. The properties of \(\prec \) are listed in Lemma 10.
The main claim is:
 iff
iff
there is a set \(M\) elements in \(K\) that are of \(\prec \)-safe with respect to \(\phi \) and jointly entail \(\psi \) iff
there is an \(M\subseteq K\) such that \(M \vdash \psi \) and for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \) and all \(\chi \in N\cap M\) there is a \(\xi \in N\) such that \(\xi \prec \chi \) iff
there is an \(M\subseteq K\) such that \(M \vdash \psi \) and for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \) and all \(\chi \in N\cap M\) there is a \(\xi \in N\) such that  and \(\nvdash \xi \)
and \(\nvdash \xi \)
This claim is trivially satisfied if \(\phi \notin K\), since then (K 3) and the fact that \(K\) is logically closed entail that both the left-hand side and the right-hand side are equivalent to \(\psi \in K\). So we suppose that \(\phi \in K\) in the following.
3) and the fact that \(K\) is logically closed entail that both the left-hand side and the right-hand side are equivalent to \(\psi \in K\). So we suppose that \(\phi \in K\) in the following.
(i) From left to right, the general case. Suppose that  . Take the set \(M = \{\phi \vee \psi , \lnot \phi \vee \psi \}\). By (K
. Take the set \(M = \{\phi \vee \psi , \lnot \phi \vee \psi \}\). By (K 1) and (K
1) and (K 2), \(M\subseteq K\). As a consequence of \(\lnot \phi \), \(\lnot \phi \vee \psi \) is not in any minimal set entailing \(\phi \), so it is \(\prec \)-safe with respect to \(\phi \). It remains to check \(\phi \vee \psi \). Suppose \(N \vdash _{min} \phi \) with \(\phi \vee \psi \) in \(N\subseteq K\). We want to show that there is a \(\xi \) in \(N\) such that
2), \(M\subseteq K\). As a consequence of \(\lnot \phi \), \(\lnot \phi \vee \psi \) is not in any minimal set entailing \(\phi \), so it is \(\prec \)-safe with respect to \(\phi \). It remains to check \(\phi \vee \psi \). Suppose \(N \vdash _{min} \phi \) with \(\phi \vee \psi \) in \(N\subseteq K\). We want to show that there is a \(\xi \) in \(N\) such that  and \(\nvdash \xi \). (Notice that the minimality condition will not be used again for this direction.)
and \(\nvdash \xi \). (Notice that the minimality condition will not be used again for this direction.)
By (K 1), we can infer from
1), we can infer from  that
that  . So by the Partial antitony condition (K
. So by the Partial antitony condition (K 7P) which is equivalent with (K
7P) which is equivalent with (K 7), we get
7), we get  , or, by (K
, or, by (K 6),
6),  . By (K
. By (K 8p) which is equivalent with (K
8p) which is equivalent with (K 8wd),
8wd),  for some \(\xi \) in \(N\). And by the minimality of \(N\), \(\nvdash \xi \), as desired.
for some \(\xi \) in \(N\). And by the minimality of \(N\), \(\nvdash \xi \), as desired.
From right to left. Suppose that there is an \(M\subseteq K\) such that \(M \vdash \psi \) and for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \) and all \(\chi \in N\cap M\) there is a \(\xi \in N\) such that  and \(\nvdash \xi \). Notice that \(\psi \) is in \(K\), by (K
and \(\nvdash \xi \). Notice that \(\psi \) is in \(K\), by (K 1).
1).
In the limiting case \(\vdash \phi \), we have \(N\vdash _{min}\phi \) if and only if \(N=\emptyset \). So the supposition reduces to \(K\vdash \psi \) or, by the fact that \(K\) is logically closed, \(\psi \in K\). But by (K 5),
5),  , so
, so  , as desired. So let us now turn to the principal case in which \(\nvdash \phi \).
, as desired. So let us now turn to the principal case in which \(\nvdash \phi \).
Let \(M'\) be a subset of \(M\) such that \(M' \vdash _{min} \phi \vee \psi \). From the supposition it follows that for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \) and all \(\chi \in N\cap M'\) there is a \(\xi \in N\) such that  and \(\nvdash \xi \). By Partial antitony (K
and \(\nvdash \xi \). By Partial antitony (K 7P), we get that for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \) and all \(\chi \in N\cap M'\),
7P), we get that for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \) and all \(\chi \in N\cap M'\),  . In short, by (K
. In short, by (K 1), for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \),
1), for all \(N\subseteq K\) such that \(N \vdash _{min} \phi \),  .
.
Suppose for reductio that \(M' \vdash \phi \). Then, since \(\nvdash \phi \), also \(\nvdash \bigwedge M'\). It follows from \(M' \vdash _{min} \phi \vee \psi \) that \(M' \vdash _{min} \phi \), and we get  , contradicting (K
, contradicting (K 4). So \(M' \nvdash \phi \).
4). So \(M' \nvdash \phi \).
Now consider the set \(N_0 = M' \cup \{\psi \!\rightarrow \!\phi \}\). Since \(K\) is logically closed and \(\phi \in K\), \(N_0 \subseteq K\). We show that \(N_0 \vdash _{min} \phi \). Since \(M'\vdash _{min}\phi \vee \psi \), clearly \(N_0\vdash \phi \). Since \(M' \nvdash \phi \), \(\psi \!\rightarrow \!\phi \) is not redundant. But neither is any element \(\rho \) of \(M'\) redundant. For suppose that \((M'-\{\rho \}) \cup \{\psi \!\rightarrow \!\phi \} \vdash \phi \). Then \(M'-\{\rho \} \vdash (\psi \!\rightarrow \!\phi )\!\rightarrow \!\phi \), i.e., \(M'-\{\rho \} \vdash \phi \vee \psi \), contradicting the minimality of \(M'\).
From the above, we get  . Now we have \(M' \subseteq N_0\), thus \(\bigwedge (N_0\cap M') = \bigwedge M'\) and
. Now we have \(M' \subseteq N_0\), thus \(\bigwedge (N_0\cap M') = \bigwedge M'\) and  . Equivalently, by (K
. Equivalently, by (K 6),
6),  . So by (K
. So by (K 4) and (K
4) and (K 8d), or alternatively by (K
8d), or alternatively by (K 8c),
8c),  , and by (K
, and by (K 1)
1)  . Finally, by (K
. Finally, by (K 5) and (K
5) and (K 1),
1),  , as desired.
, as desired.
(ii) The case of a logically finite belief set \(K\), from left to right. Suppose that  . Let \(\mathrm {Coatoms}_K(\phi \vee \psi )\) denote the set of co-atoms of \(K\), i.e., the logically weakest non-tautological elements of \(K\), that are implied by \(\phi \vee \psi \), and take the set \(M = \mathrm {Coatoms}_K(\phi \vee \psi ) \cup \{\lnot \phi \vee \psi \}\). As a consequence of \(\lnot \phi \), \(\lnot \phi \vee \psi \) is not in any minimal set entailing \(\phi \), so it is \(\prec \)-safe with respect to \(\phi \). It remains to check for every co-atom \(\alpha \) in \(\mathrm {Coatoms}_K(\phi \vee \psi )\) that it is \(\prec \)-safe with respect to \(\phi \). Suppose \(N \vdash _{min} \phi \) with \(\alpha \) in \(N\). We want to show that there is a \(\xi \) in \(N\) such that
. Let \(\mathrm {Coatoms}_K(\phi \vee \psi )\) denote the set of co-atoms of \(K\), i.e., the logically weakest non-tautological elements of \(K\), that are implied by \(\phi \vee \psi \), and take the set \(M = \mathrm {Coatoms}_K(\phi \vee \psi ) \cup \{\lnot \phi \vee \psi \}\). As a consequence of \(\lnot \phi \), \(\lnot \phi \vee \psi \) is not in any minimal set entailing \(\phi \), so it is \(\prec \)-safe with respect to \(\phi \). It remains to check for every co-atom \(\alpha \) in \(\mathrm {Coatoms}_K(\phi \vee \psi )\) that it is \(\prec \)-safe with respect to \(\phi \). Suppose \(N \vdash _{min} \phi \) with \(\alpha \) in \(N\). We want to show that there is a \(\xi \) in \(N\) such that  and \(\nvdash \xi \).
and \(\nvdash \xi \).
By (K 1), we can infer from
1), we can infer from  that
that  . So by \(\phi \vdash \alpha \) and Partial antitony (K
. So by \(\phi \vdash \alpha \) and Partial antitony (K 7P) which is equivalent with (K
7P) which is equivalent with (K 7), we get
7), we get  , or, by (K
, or, by (K 6),
6),  . By (K
. By (K 8r),
8r),  . Since \(\alpha \) is a co-atom of \(K\),
. Since \(\alpha \) is a co-atom of \(K\),  for some \(\xi \) in \(N\), by Boolean considerations.
for some \(\xi \) in \(N\), by Boolean considerations.
The right-to-left direction of the case of a logically finite belief set \(K\), is proven literally as in the general case. QED
Proof of Lemma 18. (i) Suppose that \(\phi <\psi \) and \(\psi <\phi \). Then, by Intersubstitutivity, \(\phi <(\psi \wedge \psi )\) and \(\psi <(\phi \wedge \phi )\), so by the left-to-right direction of Choice \((\phi \wedge \psi )<\psi \) and \((\psi \wedge \phi )<\phi \). By Intersubstitutivity again, \(((\phi \wedge \psi )\wedge \phi )<\psi \) and \(((\phi \wedge \psi )\wedge \psi )<\phi \). By the right-to-left direction of Choice, \((\phi \wedge \psi )<(\phi \wedge \psi )\). But this contradicts Irreflexivity. (ii)–(vi) are easy. (vii) For transitivity, let \(\phi <\psi \) and \(\psi <\chi \). Then, by Continuing down, \(\phi \wedge \chi <\psi \) and \(\phi \wedge \psi <\chi \). By the right-to-left direction of Choice, it follows that \(\phi <\psi \wedge \chi \). So by Continuing up, \(\phi <\chi \). Acyclicity follows from Transitivity and Irreflexivity. (viii) For the first part, assume that for all \(\beta _j\) there is an \(\alpha _i\) such that \(\alpha _i < \beta _j\). By Continuing down, for all \(\beta _j\), it holds that \(\bigwedge \alpha _i < \beta _j\). So by Conjunction up, which follows from Continuing down and the right-to-left direction of Choice (see part (iv) of this lemma), \(\bigwedge \alpha _i < \bigwedge \beta _j\), as desired. For the second part, assume that \(\bigwedge \alpha _i < \bigwedge \beta _j\). By Continuing up, \(\bigwedge \alpha _i < \beta _j\) for all \(\beta _j\). Take an arbitrary such \(\beta _j\). Now repeated application of (EII\(^-\)) tells us that there are sentences \(\phi _j^1, \dots , \phi _j^k\) such that \(\beta _j \dashv \vdash \phi _j^1\wedge \dots \wedge \phi _j^k\) and for all \(i=1,\dots ,n\), \(\alpha _i\wedge \beta _j < \phi _j^i\). But since \(\beta _j\) is a co-atom of \(K\), it follows from Boolean considerations that each \(\phi _j^i\) is either a tautology or equivalent with \(\beta _j\) and that in fact at least one of the \(\phi _j^i\)’s is equivalent with \(\beta _j\). It follows from Intersubstitutivity that \(\alpha _i\wedge \beta _j < \beta _j\) for at least one \(i\), and the right-to-left direction of Choice and Intersubstitutivity once more that \(\alpha _i < \beta _j\) for at least one \(\alpha _i\). But this is what we wanted to prove. QED
Proof of Lemma 19. That (ii) implies (i) is trivial. Take \(M\) from (ii) and notice that every \(N\) that minimally implies \(\phi \wedge \psi \) obviously implies \(\phi \).
Now we show that (i) implies (ii), given Transitivity and Continuing down for \(\prec \). Take \(M\) from (i) and let \(M'\) be a subset of \(M\) that minimally implies \(\psi \). Obviously \(M'\) also satisfies (i), and by compactness, \(M'\) is finite. Suppose that \(N\vdash \phi \). Put \(N' = \{(\bigwedge M') \!\rightarrow \!\xi : \xi \in N\}\). Since \(M'\cup N\vdash \phi \wedge \psi \), also \(M'\cup N'\vdash \phi \wedge \psi \). Let \(S\) be a minimal subset of \(M'\cup N'\) that implies \(\phi \wedge \psi \). First notice that \(M'\subseteq S\), because if some \(\chi \) from \(M'\) were missing from \(S\), then \(S\) could not imply \(\phi \). For suppose that \((M'-\{\chi \})\cup N' \vdash \phi \wedge \psi \). Then, since \(\lnot \psi \) is logically stronger than \(\lnot \bigwedge M'\) and thus than \(N'\), we get that \((M'-\{\chi \})\cup \{\lnot \psi \} \vdash \phi \wedge \psi \), and thus \(M'-\{\chi \} \vdash \psi \vee (\phi \wedge \psi )\), contradicting the minimality of \(M'\). So since \(S\vdash _{min}\phi \wedge \psi \), we can apply (i) and find that \(S\) is non-empty and for every \(\chi \) in \(M'\cap S = M'\) there is a \(\xi \) in \(S\) such that \(\xi \prec \chi \). Now this \(\xi \) is either in \(M'\) or in \(N'\). But if it is in \(M'\), we can apply (i) again and find another sentence \(\xi ^1\) with \(\xi ^1\prec \xi \) which again is either in \(M'\) or in \(N'\). If \(\xi ^1\) is in \(M'\), we repeat the process again, and so on. Since \(M'\) is finite and \(\prec \) is acyclic and transitive, there must finally be a \(\xi ^n\) with \(\xi ^n\prec \chi \) which is not in \(M'\) but in \(N'\). This \(\xi ^n\) is of the form \((\bigwedge M') \!\rightarrow \!\rho \) for some \(\rho \) in \(N\). Since, finally, this \(\rho \) implies \(\xi ^n\) and \(\prec \) continues down \(\vdash \) over \(K\), \(\rho \prec \chi \), as desired. QED
Proof of Theorem 21. By Theorem 4, every safe contraction function  over \(K\) satisfies (K
over \(K\) satisfies (K 1) \(-\) (K
1) \(-\) (K 6). We now show that (EC) follows from (CE), provided that
6). We now show that (EC) follows from (CE), provided that  satisfies (K
satisfies (K 1), (K
1), (K 2), (K
2), (K 5) and (K
5) and (K 6).Footnote 30 (CE) gives us:
6).Footnote 30 (CE) gives us:

By (K 6), this is equivalent with
6), this is equivalent with

For (EC), we need to show that
 iff \(\psi \in K\) and either \(\phi < \phi \vee \psi \) or \(\vdash \phi \)
iff \(\psi \in K\) and either \(\phi < \phi \vee \psi \) or \(\vdash \phi \)
Let  . By (K
. By (K 2), \(\psi \in K\). By (K
2), \(\psi \in K\). By (K 1),
1),  . Suppose that \(\nvdash \phi \). Then, by (\(\dag \)), \(\phi < \phi \vee \psi \), as desired.
. Suppose that \(\nvdash \phi \). Then, by (\(\dag \)), \(\phi < \phi \vee \psi \), as desired.
For the converse, let \(\psi \in K\) and either \(\phi < \phi \vee \psi \) or \(\vdash \phi \). If firstly \(\phi < \phi \vee \psi \), then by (\(\dag \))  . Since \(\psi \in K\), we get
. Since \(\psi \in K\), we get  , by (K
, by (K 5) and (K
5) and (K 1). Thus by (K
1). Thus by (K 1)
1)  , as desired. If secondly \(\vdash \phi \), then
, as desired. If secondly \(\vdash \phi \), then  , by (K
, by (K 5), so again
5), so again  , as desired. QED
, as desired. QED
Proof of Theorem 22. Since \(<\) is a generalized entrenchment relation, it is acyclic, by Lemma 18 (vii), and can thus be used as a hierarchy for a safe contraction. Let \(\psi \) be in \(K\). The case when \(\vdash \psi \) is trivial so we assume that \(\nvdash \psi \). Then  acccording to the entrenchment-based contraction (EC) iff
acccording to the entrenchment-based contraction (EC) iff
(i) \(\phi <\phi \vee \psi \)
\(\psi \) is in  acccording to the safe contraction defined in Definition 2 iff
acccording to the safe contraction defined in Definition 2 iff
(ii) there is a set \(M\) of \(\phi \)-safe elements such that \(M\vdash \psi \)
First, we show that (i) implies (ii). Suppose that \(\phi <\phi \vee \psi \). From this we get, by Intersubstitutivity and the right-to-left direction of Choice, \(\phi \vee \lnot \psi < \phi \vee \psi \). Now consider the set \(M = \{\phi \vee \psi , \lnot \phi \vee \psi \}\). We show that this set is suitable for (ii). \(\lnot \phi \vee \psi \) is \(\phi \)-safe anyway, because it is a consequence of \(\lnot \phi \) and thus will not be included in any minimal set implying \(\phi \). It remains to show that \(\phi \vee \psi \) is \(\phi \)-safe as well. Suppose that \(\phi \vee \psi \) is in \(N\) for some \(N\) such that \(N \vdash _{min} \phi \). Notice that \(N\) is finite and that \(N-\{\phi \vee \psi \} \vdash \phi \vee \lnot \psi \). Thus, by Continuing down, \(\bigwedge (N-\{\phi \vee \psi \}) < \phi \vee \psi \), and by repeated application of (EII), we get that there is some \(\chi \) in \(N-\{\phi \vee \psi \}\) such that \(\chi < \phi \vee \psi \). Thus \(\phi \vee \psi \) is \(\phi \)-safe, and this proves (ii).
Second, we show that (ii) implies (i). Pick an \(M\) from (ii). If \(N \vdash _{min} \phi \) and \(\chi \) is in \(M\cap N\), then there is a \(\xi \) in \(N\) such that \(\xi < \chi \). Take some subset \(M'\subseteq M\) such that \(M' \vdash _{min} \phi \vee \psi \). Then, if \(N \vdash _{min} \phi \) and \(\chi \) is in \(M'\cap N\), there is a \(\xi \) in \(N\) such that \(\xi < \chi \). By Continuing down, \(\bigwedge N < \chi \). By repeated application of Conjunction up, which follows from Continuing down (by Lemma 18 (iv)), \(\bigwedge N < \bigwedge (M'\cap N)\).
Now we show that \(M' \nvdash \phi \). Suppose for reductio that \(M' \vdash \phi \). Then, since \(\nvdash \phi \), also \(\nvdash \bigwedge M'\). It follows from \(M' \vdash _{min} \phi \vee \psi \) that \(M' \vdash _{min} \phi \), and we get  , contradicting (K
, contradicting (K 4).
4).
Now consider the set \(N_0 = M' \cup \{\psi \!\rightarrow \!\phi \}\). It follows from \(M' \vdash \phi \vee \psi \) that \(N_0 \vdash \phi \). Since \(M' \nvdash \phi \), \(\psi \!\rightarrow \!\phi \) is not redundant. Suppose that some \(\rho \in M'\) is redundant. Then \(M'-\{\rho \} \cup \{ \psi \!\rightarrow \!\phi \} \vdash \phi \) and consequently \(M'- \{\rho \} \vdash \phi \vee \psi \), contrary to \(M' \vdash _{min} \phi \vee \psi \). We therefore have \(N_0 \vdash _{min} \phi \).
This gives us \(\bigwedge N_0 < \bigwedge (M'\cap N_0)\) and since \(N_0 = M' \cup \{\psi \!\rightarrow \!\phi \}\), \(\bigwedge N_0 < \bigwedge M'\). By the right-to-left direction of Choice, \(\psi \!\rightarrow \!\phi < \bigwedge M'\), and by Continuing up and Continuing down \(\phi < \phi \vee \psi \), i.e. we have (i) as desired. QED
Proof of Theorem 27. Let the language have only the two propositional variables \(p\) and \(q\), and let \(K = \mathrm {Cn}(p \wedge q)\). Let \(*\) be a revision function on \(K\) such that \(K*\lnot p = Cn(\lnot p \wedge q)\), \(K*\lnot q = Cn(\lnot p \wedge \lnot q)\), and \(K*\lnot (p\leftrightarrow q) = Cn( p \wedge \lnot q)\).
\(K\bot p = \{\mathrm {Cn}(q), \mathrm {Cn}(p\leftrightarrow q)\}\), and therefore  is either \(\mathrm {Cn}(q)\), \(\mathrm {Cn}(p \leftrightarrow q)\), or \(\mathrm {Cn}(p \rightarrow q)\). Of these only \(\mathrm {Cn}(q)\) satisfies the Levi identity
is either \(\mathrm {Cn}(q)\), \(\mathrm {Cn}(p \leftrightarrow q)\), or \(\mathrm {Cn}(p \rightarrow q)\). Of these only \(\mathrm {Cn}(q)\) satisfies the Levi identity  . Thus
. Thus  .
.
\(K\bot q = \{\mathrm {Cn}(p), \mathrm {Cn}(p\leftrightarrow q)\}\), and therefore  is either \(\mathrm {Cn}(p)\), \(\mathrm {Cn}(p \leftrightarrow q)\), or \(\mathrm {Cn}(q \rightarrow p)\). Of these only \(\mathrm {Cn}(p \leftrightarrow q)\) satisfies the Levi identity
is either \(\mathrm {Cn}(p)\), \(\mathrm {Cn}(p \leftrightarrow q)\), or \(\mathrm {Cn}(q \rightarrow p)\). Of these only \(\mathrm {Cn}(p \leftrightarrow q)\) satisfies the Levi identity  . Thus
. Thus  .
.
\(K\bot (p \leftrightarrow q)= \{\mathrm {Cn}(p), \mathrm {Cn}(q)\}\), and therefore  is either \(\mathrm {Cn}(p)\), \(\mathrm {Cn}(q)\), or \(\mathrm {Cn}(p \vee q)\). Of these only \(\mathrm {Cn}(p)\) satisfies the Levi identity
is either \(\mathrm {Cn}(p)\), \(\mathrm {Cn}(q)\), or \(\mathrm {Cn}(p \vee q)\). Of these only \(\mathrm {Cn}(p)\) satisfies the Levi identity  . Thus
. Thus  .
.
Thus we have  ,
,  , and
, and  . It was shown in the proof of Theorem 6 that this contraction function is not reconstructible as a safe contraction, and consequently \(*\) is not reconstructible as a safe revision. QED
. It was shown in the proof of Theorem 6 that this contraction function is not reconstructible as a safe contraction, and consequently \(*\) is not reconstructible as a safe revision. QED
Rights and permissions
Copyright information
© 2014 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Rott, H., Hansson, S.O. (2014). Safe Contraction Revisited. In: Hansson, S. (eds) David Makinson on Classical Methods for Non-Classical Problems. Outstanding Contributions to Logic, vol 3. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-7759-0_4
Download citation
DOI: https://doi.org/10.1007/978-94-007-7759-0_4
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-7758-3
Online ISBN: 978-94-007-7759-0
eBook Packages: Humanities, Social Sciences and LawPhilosophy and Religion (R0)


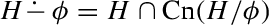 .
. Trans) and (K
Trans) and (K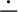 Acyc). Translated into the language of contractions, it reads thus: If for all
Acyc). Translated into the language of contractions, it reads thus: If for all 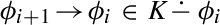 and furthermore
and furthermore 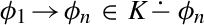 , then
, then 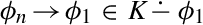 .
.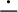 8r
8r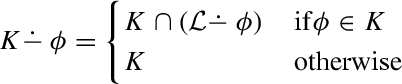
 (Redundancy).
(Redundancy). by
by 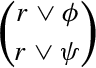 .
.
 1) – (K
1) – (K 7), (K
7), (K 8c) and (K
8c) and (K 8r), but not (K
8r), but not (K 8wd). Read “” as“
8wd). Read “” as“ 