Rationalizable behavior in the Hotelling–Downs model of spatial competition

Abstract

We consider two scenarios of the Hotelling–Downs model of spatial competition. This setting has typically been explored using pure Nash equilibrium, but this paper uses point rationalizability (Bernheim, Econometrica J Economet Soc 52(4):1007–1028, 1984) instead. Pure Nash equilibrium imposes a correct beliefs assumption, which may rule out perfectly reasonable choices in a game. Point rationalizability does not have this correct beliefs assumption, which makes this solution concept more natural and permissive. The first scenario is the original Hotelling–Downs model with an arbitrary number of agents. Eaton and Lipsey (Rev Econ Stud 42(1):27–49, 1975) used pure Nash equilibrium as their solution concept for this setting. They showed that with three agents, there does not exist a pure Nash equilibrium. We characterize the set of point rationalizable choices for any number of agents and show that as the number of agents increases, the set of point rationalizable choices increases as well. In the second scenario, agents have limited attraction intervals (Feldman et al. Variations on the Hotelling–Downs model. In: Thirtieth AAAI Conference on Artificial Intelligence, pp 496–501, 2016). We show that the set of point rationalizable choices does not depend on the number of agents, apart from this number being odd or even. Furthermore, the set of point rationalizable choices shrinks as the attraction interval increases.

1 Introduction

Hotelling’s (1929) paper on the duopoly location model was published almost a century ago, yet the contents of the paper are still taught today in economics courses all over the world. The paper contains a rich motivation and intuitive examples that explain the results from the model. Hotelling was the first to include the location of the firm as a feature in his model. The location model demonstrates the relationship between the pricing and location of a firm. Consumers are uniformly distributed on a line segment, and incur a transportation cost for the distance traveled to one of the firms. This allows for the feature that when a firm increases its price, it will gradually lose demand instead of instantaneously, which is the case for the Bertrand model.

Downs (1957) gave a different interpretation to Hotelling’s model, in the case where each firm charges an identical price. The firms could then be interpreted as political agents in a society with political views that can be ordered from left to right. These agents simultaneously choose a political position on the line. Instead of consumers, Downs’ model consists of voters that will support the agent whose position is closest to their preferred political position.

Most papers on the Hotelling–Downs model use the pure Nash equilibrium as a solution concept. Eaton and Lipsey (1975) analyzed the Hotelling–Downs model with an arbitrary number of firms, where all agents simultaneously choose their position. For three agents, they mention that it is impossible to satisfy the equilibrium conditions, and as a result there is no pure Nash equilibrium. For any other number of agents, they are able to find one or multiple equilibria.

Pearce (1984) and Bernheim (1984) criticized the Nash equilibrium concept and independently developed a different solution concept, called rationalizability. Their main critique was that the Nash equilibrium is too restrictive in its assumptions, partially explaining why no Nash equilibrium was established in Eaton and Lipsey’s model with three firms. Rationalizability requires that each player believes that his opponents play rationally, believes that his opponents believe that the other players play rationally, and so on. Nash equilibrium on the other hand only requires that each player believes that the other players play rationally (Aumann & Brandenburger, 1995). Additionally, Nash equilibrium imposes a correct belief assumption, while rationalizability does not. The correct belief assumption states that each player must believe that his opponents are correct about his own beliefs, and that his opponents share his own beliefs about other players. Because rationalizability does not impose this constraint, it is more natural and permissive than Nash equilibrium.

This paper characterizes the set of point rationalizable choices of each agent instead of the set of rationalizable choices. The main difference between rationalizability and point rationalizability is that point rationalizability only considers point beliefs, while rationalizability considers mixed beliefs as well. In this paper, point beliefs assign probability 1 to exactly one of each of the opponents’ pure choices. In most of the literature regarding the Hotelling–Downs model, the emphasis has been on finding the pure Nash equilibria. Mixed beliefs are not considered in a pure Nash equilibrium. Because we want to compare our results with pure Nash equilibria, point rationalizability is the preferred solution concept over rationalizability. Luo (2016) provides an additional reason for favoring point rationalizability over rationalizability. He argues that rationalizability can show a lack of truth, and provides true rationalizability as a new formulation. True rationalizability is mathematically equivalent to Bernheim’s (1984) definition of point rationalizability, where each player assigns probability 1 to a combination of mixed choices of the opponents. As a result, the point rationalizable choices of each agent we consider in this paper are also truly rationalizable.

Our first result is a characterization of the set of point rationalizable choices in the original Hotelling–Downs model with an arbitrary number of agents. As the number of agents increases, the set of point rationalizable choices for each agent increases as well. When the number of agents gets very large, almost any position is point rationalizable, except the extreme positions on the line. We will compare our characterization to the results of Eaton and Lipsey (1975). We find that the positions chosen by the agents in a pure Nash equilibrium are further from the edges of the line than the point rationalizable choices closest to the edges.

Second, we characterize the point rationalizable choices of a more recent variation of the Hotelling–Downs model, introduced by Feldman et al. (2016). In this variation, clients are attracted to all agents within their attraction interval. As a result, it is possible for a client in this model to abstain from supporting any agent. We consider attraction intervals ranging from 0 to 1. We find that as the attraction interval increases, the set of point rationalizable choices decreases. The set of point rationalizable choices is not decreasing in the number of agents, but we do find different results depending on whether the number of agents is odd or even. When the attraction interval equals 1, only the middle position on the line is point rationalizable.

Section 2 introduces the Hotelling–Downs model and defines point rationalizability. Section 3 contains the results of the original Hotelling–Downs model with an arbitrary number of agents. Section 4 introduces the Hotelling–Downs model with limited attraction and characterizes the point rationalizable choices in relation to the size of the attraction interval. Section 5 contains a discussion and conclusion. All proofs are collected in the appendix.

2 Hotelling–Downs model and rationalizability

Let $I=\{1,\ldots ,N\}$ denote the set of agents. Each agent $i \in I$ simultaneously selects a choice $c_i \in C_i$, where $C_i=\{0,\delta ,2\delta ,\ldots ,1-\delta ,1\}$ denotes the set of positions that agent i can choose, where $\delta =\frac{1}{m}$ for some strictly positive integer m. Clients are distributed uniformly on the interval [0, 1]. Clients will support an agent whose position is closest to the client. In the case that the client is equally close to multiple agents, he will randomly select one of these agents to support.

Agents are assumed to be support maximizers, meaning that their objective is to attract as many clients as possible. Hence, the utility for each agent i will be denoted by the fraction of clients that support agent i. Let $C_{-i}=C_1 \times \cdots \times C_{i-1} \times C_{i+1} \times \cdots \times C_N$ denote the set that contains all the choice combinations of the opponents of agent i, where $c_{-i}=(c_1,\ldots ,c_{i-1},c_{i+1},\ldots ,c_N) \in C_{-i}$.

Given a choice $c_i \in C_i$ and a choice combination of the opponents $c_{-i}\in C_{-i}$, let $l_i(c_i,c_{-i})$ denote the position of the closest opponent to the left of agent i, in case it exists. Let $r_i(c_i,c_{-i})$ denote the position of the closest opponent to the right of agent i, in case it exists. Let $D_i(c_i,c_{-i})$ denote the number of agents that occupy position $c_i$. A choice is called leftmost if it is (one of) the position(s) closest to 0. Similarly, a choice is called rightmost if it is (one of) the position(s) closest to 1. A choice is called middle if some choices of the opponents are closer to 0 and 1.

Fig. 1

Rightmost choice

Figure 1 shows the position of the relevant indifferent client when agent i’s choice $c_i$ is rightmost. Because $c_i$ is rightmost, there are no other agents occupying a position to the right of $c_i$. The indifferent client ${\hat{x}}$ is positioned in the middle between $c_i$ and $l_i(c_i,c_{-i})$. Every client to the right of ${\hat{x}}$ will support the position $c_i$. If agent i is the only agent positioned at $c_i$, his utility is equal to $1-{\hat{x}} =1-\frac{c_i+l_i(c_i,c_{-i})}{2}=\frac{2-c_i-l_i(c_i,c_{-i})}{2}$. If the number of agents positioned at $c_i$ is equal to $D_i(c_i,c_{-i})$, then the utility of agent i is $\frac{2-c_i-l_i(c_i,c_{-i})}{2D_i(c_i,c_{-i})}$. A similar procedure can be followed for leftmost and middle choices. We can now write down the utility function for each agent i:

$$\begin{aligned} u_i(c_i,c_{-i}) = {\left\{ \begin{array}{ll} \frac{2-c_i-l_i(c_i,c_{-i})}{2D_i(c_i,c_{-i}) } &{} \text {if} \ c_i \ \text {is rightmost } \\ \frac{r_i(c_i,c_{-i})-l_i(c_i,c_{-i})}{2D_i(c_i,c_{-i})} &{} \text {if}\ c_i \ \text {is middle} \\ \frac{c_i+r_i(c_i,c_{-i})}{2D_i(c_i,c_{-i})} &{} \text {if} \ c_i \ \text {is leftmost}\\ \frac{1}{N} &{} \text {if} \ \text {all agents are positioned at} \ c_i \\ \end{array}\right. } \end{aligned}$$

Each agent i can motivate his choice by forming a belief about the opponents’ choice combinations $C_{-i}$. A belief for agent i is a probability distribution $b_i$ over the set $C_{-i}$. For every choice combination of the opponents $c_{-i}$, the belief $b_i(c_{-i})$ denotes the probability that agent i assigns to the event that this particular choice combination is indeed chosen by the opponents. We only consider point beliefs in pure choices. That is, we only consider beliefs where $b_i(c_{-i})=1$, for some opponents’ choice combination $c_{-i}$. Expected utility can be denoted as $u_i(c_i,b_i)= \sum _{c_{-i}\in C_{-i}}b_i(c_{-i})u_i(c_i,c_{-i})$. A choice is optimal for an agent if it maximizes his utility for some belief.

Definition 1

A choice $c_i\in C_i$ is optimal for agent i given a belief $b_i$ if $\forall \ c_i^{*}\in C_i$,

$$\begin{aligned} u_i(c_i,b_i) \ge u_i(c_i^{*},b_i). \end{aligned}$$

If $c_i \in A_i \subseteq C_i$ and the above inequality holds for every $c_i^{*}\in A_i$, then $c_i$ is optimal in $A_i$ for the belief $b_i$.

A choice is (point) rational for agent i if this choice is optimal for some (point) belief $b_i$.

Note that if the choice set of each agent i would be infinite, such as $C_i=[0,1]$, then for almost all point beliefs of an agent i, an optimal choice would not exist.

The following inductive procedure to find the point rationalizable choices resembles Pearce’s (1984) procedure, adapted for point beliefs in pure choices. It is thus a refinement of true rationalizability (Luo, 2016), which is equivalent to a version of point rationalizability where players assign probability 1 to a combination of mixed choices for the opponents.

Definition 2

Let $P_i(0)= C_i$ for all $i \in I$. Then $P_i(k)$ is inductively defined for $k=1,2,...$ by $P_i(k)=\{c_i \in P_i(k-1):\ \text {there exists}$ a point belief $b_i$ over the set $P_{-i}(k-1)$ such that $c_i$ is optimal in $P_i(k-1)$ given $b_i \}$. The set of point rationalizable choices for agent i is then $P_i={\bigcap }_{k=1}^\infty P_i(k)$.

3 Results for the original Hotelling–Downs model

The next theorem uses a ceiling function. The ceiling function $\left\lceil {a}\right\rceil$ returns the smallest value b bigger or equal to a such that b is a multiple of $\delta$.

Theorem 1

Suppose there are $N \ge 2$ agents and let $\delta \le \frac{1}{3(N-3)+6}$. Then $\forall i \in I$,

$$\begin{aligned} P_i=\left\{ \left\lceil {\frac{1-(N-1)\delta }{2N-2}}\right\rceil ,\ldots , 1- \left\lceil {\frac{1-(N-1)\delta }{2N-2}}\right\rceil \right\} \text {\ if\ } N\in \{2,3\} \\ P_i=\left\{ \left\lceil {\frac{1-(N-2)\delta }{2N-2}}\right\rceil ,\ldots , 1- \left\lceil {\frac{1-(N-2)\delta }{2N-2}}\right\rceil \right\} \text {\ if\ } N \ge 4. \end{aligned}$$

If $\delta$ approaches zero, then

$$\begin{aligned} P_i=\left[ \frac{1}{2N-2}, \frac{2N-3}{2N-2}\right] \ \forall N \ge 2. \end{aligned}$$

Fig. 2

Beliefs diagram

An immediate result from this theorem is that the set of point rationalizable choices grows as the number of agents increases. With two agents, we are able to use the fact that as long as $k \le \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$, in each round $P_i(k)$, the choice $k\delta$ is strictly dominated by the choice $(k+1)\delta$. A similar result is true at the other side of the line. Hence, for two agents, only the middle choice(s) survive(s) the iterative procedure. However, with three or more agents this is no longer true.

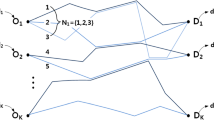
For example, consider 3 agents and $\delta =0.1$. The point rationalizable choices for each agent are then given by $\left\{ \left\lceil {\frac{1-2\delta }{4}}\right\rceil ,\ldots ,1-\left\lceil {\frac{1-2\delta }{4}}\right\rceil \right\} = \left\{ \frac{2}{10}, \frac{3}{10},\frac{4}{10},\frac{5}{10},\frac{6}{10},\frac{7}{10},\frac{8}{10}\right\}$. A beliefs diagram (Perea, 2012) helps to visually show the reasoning of each agent in a game. The arrows represent the beliefs of an agent. For example, consider the arrow from agent 1 with the choice $\frac{2}{10}$ going to the choice pair $\left( \frac{3}{10},\frac{7}{10}\right)$ of agent 2 and 3. This arrow represents that choice $\frac{2}{10}$ of agent 1 is supported by the belief that agent 2 chooses $\frac{3}{10}$ and agent 3 chooses $\frac{7}{10}$. This is a first-order belief of agent 1 that supports his choice of $\frac{2}{10}$. By following the arrows, we can also find the higher order beliefs. The choice $\frac{2}{10}$ of agent 1 is supported by the second-order belief that agent 2 believes that agent 1 and 3 choose $\frac{2}{10}$ and that agent 3 believes that agent 1 and 2 choose $\frac{8}{10}$. Continuing this way ad infinitum would give us the belief hierarchy of agent 1 that supports his choice $\frac{2}{10}$. Similarly, we can construct belief hierarchies that support the choices $\frac{3}{10},\ldots ,\frac{8}{10}$ of agent 1 or of a different agent. All these belief hierarchies express common belief in rationality, because this belief diagram only consists of the choices in $P_i=\left\{ \frac{2}{10}, \frac{3}{10},\frac{4}{10},\frac{5}{10},\frac{6}{10},\frac{7}{10},\frac{8}{10}\right\}$. Hence, these belief hierarchies support the point rationalizable choices.

We are particularly interested in the set of point rationalizable choices if $\delta$ approaches 0. When $N \ge 2$ and $\delta$ approaches zero, the set of point rationalizable choices is given by $\left[ \frac{1}{2N-2},\ldots ,\frac{2N-3}{2N-2}\right]$. Table 1 shows the set of point rationalizable choices for the first eight agents when $\delta$ approaches zero. As N increases, the set of point rationalizable choices also increases. When N becomes very large, the set of point rationalizable choices approaches the interval (0, 1).

Eaton and Lipsey (1975) investigated how robust the minimum differentiation result from the Hotelling model with identical prices is to changes in the model. The main differences between their model and our model are the choice sets and how many agents can occupy a location. In Eaton and Lipsey’s model, agents can choose any location in [0, 1] and only one agent can occupy a given location. Between each agent there must be a distance of at least $\delta$, which is very small relative to the line segment and market. They find at least one Nash equilibrium for any number of agents, except three agents. The Nash equilibria up to five agents are unique, and from six agents onwards there are an infinite number of Nash equilibria. In our model, the choice set is finite and agents are allowed to occupy the same position. Furthermore, we do find a set of point rationalizable choices for any number of agents.

Table 1 Set of point rationalizable choices when $\delta$ approaches 0 and positions of the extreme agents in the pure Nash equilibrium with maximum distance between middle agents

In the pure Nash equilibrium with two agents, both are positioned at the center of the line, equivalent to the minimal differentiation result of Hotelling (1929). For four agents, Eaton and Lipsey find the unique equilibrium where agent 1 and 2 are positioned on $\frac{1}{4}$, and agent 3 and 4 are positioned at $\frac{3}{4}$. For five agents, Eaton and Lipsey find the unique equilibrium where agent 1 and 2 are positioned at $\frac{1}{6}$, agent 3 is positioned at the middle of the line, and agent 4 and 5 are positioned at $\frac{5}{6}$.

For six agents onward the equilibrium is no longer unique. The equilibrium that minimizes the distance between middle agents is given by agent 1 and 2 positioning at $\frac{1}{6}$, agent 3 and 4 positioning at the middle of the line, and agent 5 and 6 positioning at $\frac{5}{6}$. The equilibrium that maximizes the distance between middle agents is given by agent 1 and 2 positioning at $\frac{1}{8}$, agent 3 at $\frac{3}{8}$, agent 4 at $\frac{5}{8}$, and agent 5 and 6 positioning at $\frac{7}{8}$.

In general, if $N \ge 4$, we have that the position of the extreme agents in the Nash equilibria found by Eaton and Lipsey is further from the edge of the line than the extreme point rationalizable choices. For the Nash equilibrium that maximizes the distance between the middle agents, we have another relationship with the point rationalizable choices of an agent. The position of the agents that are positioned at the most extreme positions in the N agent Nash equilibrium are exactly the extreme point rationalizable positions that can be chosen if there are $N-1$ agents in the model. Table 1 depicts this relationship.

Shaked (1982) wrote a short note about the existence of a symmetric mixed strategy Nash equilibrium for the three agent Hotelling–Downs model. He demonstrated that the symmetric mixed strategy Nash equilibrium is given by each agent avoiding the extreme quartiles of the line and choosing the remaining positions with equal probability. Hence, in this symmetric mixed Nash equilibrium an agent chooses each point rationalizable choice with equal probability.

4 Hotelling–Downs model with limited attraction

Feldman et al. (2016) altered the standard Hotelling–Downs model. In this variation, clients do not necessarily choose the closest agent. Each agent i has an attraction region, given by $\omega$. Given his position on the line $c_i$, he attracts clients in between $c_i-\frac{\omega }{2}$ and $c_i+\frac{\omega }{2}$. A client positioned at x on the line will equally divide his support among the agents within $x-\frac{\omega }{2}$ and $x+\frac{\omega }{2}$. If no agent is positioned within $x-\frac{\omega }{2}$ and $x+\frac{\omega }{2}$, then the client will not support any agent. If we take the perspective of some agent i, then the set of opponent agents that attract client x can be denoted by $I_x (c_{-i})=\left\{ j\in \left\{ 1,\ldots ,i-i,i+1,\ldots ,N\right\} | x \in [c_j-\frac{\omega }{2}, c_j+\frac{\omega }{2}]\right\}$. If agent i chooses a position $c_i$ such that $x \in [c_i-\frac{\omega }{2}, c_i+\frac{\omega }{2}]$, then we can denote agent i’s share of client x as

$$\begin{aligned} a_{x,i}(c_{-i})=\frac{1}{|I_x(c_{-i})|+1}. \end{aligned}$$

Assuming a uniform distribution of the clients with density $f(x)=1 \ \forall x \in [0,1]$, the utility function of each agent i is given by

$$\begin{aligned} u_i(c_i,c_{-i})=\int _{c_i-\frac{\omega }{2}}^{c_i+\frac{\omega }{2}} a_{x,i}(c_{-i})f(x) \, \textrm{d}x. \end{aligned}$$

If agent i chooses in $[\frac{\omega }{2},1-\frac{\omega }{2}]$, then we are able to write the utility of agent i as $\int _{c_i-\frac{\omega }{2}}^{c_i+\frac{\omega }{2}} a_{x,i}\, \textrm{d}x$ instead of $\int _{c_i-\frac{\omega }{2}}^{c_i+\frac{\omega }{2}} a_{x,i}f(x) \, \textrm{d}x$. However, if agent i chooses for example $c_i=0$, then agent i’s utility is $\int _{0-\frac{\omega }{2}}^{0+\frac{\omega }{2}} a_{x,i}f(x) \, \textrm{d}x=\int _{0}^{\frac{\omega }{2}} a_{x,i} \, \textrm{d}x$. Hence, if agent i chooses a position in $[0,\frac{\omega }{2})$ or $(1-\frac{\omega }{2},1]$, we cannot omit f(x). We characterize the set of the point rationalizable choices for $0 < \omega \le 1$ and an arbitrary number of agents. Note that for any $\omega \ge 1$, an agent can simply position at the middle of the line, attracting all clients.

Fig. 3

Point rationalizable choices for an odd number of agents

Theorem 2

Consider a Hotelling–Downs model with limited attraction and let $0 <\omega \le 1$. If the number of agents is odd, then $\forall \ i\in I$,

$$\begin{aligned} P_i=[\frac{\omega }{2},1-\frac{\omega }{2}]. \end{aligned}$$

If the number of agents is even, then

$$\begin{aligned} \text {if} \ 0< \omega \le \frac{1}{3}, \ \text {then}, P_i= & {} \left[ \frac{\omega }{2},1-\frac{\omega }{2}\right] , \\ \text {if} \ \frac{1}{3}< \omega \le \frac{1}{2}, \ \text {then}, P_i= & {} \left\{ \left[ \frac{\omega }{2},1-1.5\omega \right] ,\left[ 1.5\omega ,1-\frac{\omega }{2}\right] \right\} , \\ \text {if} \ \frac{1}{2} < \omega \le 1, \ \text {then}, P_i= & {} \left\{ \frac{\omega }{2},1-\frac{\omega }{2} \right\} . \end{aligned}$$

Fig. 4

Point rationalizable choices for an even number of agents

Figures 3 and 4 graphically show the point rationalizable choices for an odd number of agents and an even number of agents, respectively. Intuitively, a rational agent should not position too close to the end of the line. If he does, he can receive a greater utility by positioning a little bit more in the direction of the center of the line, no matter what the other agents choose. As a result, for any $\omega$, the positions $[0,\frac{\omega }{2})$ and $(1-\frac{\omega }{2},1]$ are too close to the end of the line for a rational agent.

Figure 5 shows an example if $\omega \le \frac{1}{3}$. Let there be four agents and consider agent 1, who believes that all his opponents will position at $1-\frac{\omega }{2}$. If agent 1 can choose a position to the right of $\frac{\omega }{2}$, such that there are no other agents within his attraction region, then this choice is optimal, as this will give him his highest possible utility. By positioning at $\frac{1}{2}$, agent 1 will attract clients in between $\frac{1}{2}-\frac{\omega }{2}$ and $\frac{1}{2}+\frac{\omega }{2}$. Agent 1’s opponents attract clients in between $1- \omega$ and 1. Agent 1 does not share any clients with other agents if $\frac{1}{2}+\frac{\omega }{2} \le 1-\omega$, which implies $\omega \le \frac{1}{3}$. If agent 1’s choice $\frac{1}{2}$ is optimal for this belief, then any choice in $[\frac{\omega }{2},\frac{1}{2}]$ is optimal for this belief, as these choices are positioned even further away from the positions chosen by the opponents. By symmetry, agent 1’s choices in $[\frac{1}{2},1-\frac{\omega }{2}]$ are optimal for the belief that agent 1’s opponents are positioned at $\frac{\omega }{2}$. Hence, the set of point rationalizable choices is given by $[\frac{\omega }{2},1-\frac{\omega }{2}]$.

If $\omega > \frac{1}{3}$ and for an odd number of agents, we can show that all the choices in $[\frac{\omega }{2},1-\frac{\omega }{2}]$ are optimal for agent i for some point belief consisting of choices of the opponents in $[\frac{\omega }{2},1-\frac{\omega }{2}]$. Some or all of these choices are motivated by the point belief that half of his opponents are positioned at $\frac{\omega }{2}$, and half of his opponents are positioned at $1-\frac{\omega }{2}$. Hence, for an odd number of agents, the set of point rationalizable choices is given by $P_i=[\frac{\omega }{2},1-\frac{\omega }{2}]$. As a result, the set of point rationalizable choices shrinks as $\omega$ increases.

For an even number of agents and some agent i, the point belief that half of his opponents are positioned at $\frac{\omega }{2}$, and half of his opponents are positioned at $1-\frac{\omega }{2}$ does not exist. If $\frac{1}{3}< \omega < \frac{1}{2}$, then there does not exist a point belief of agent i in $[\frac{\omega }{2},1-\frac{\omega }{2}] \times \cdots \times [\frac{\omega }{2},1-\frac{\omega }{2}]$, such that his choice $c_i\in (1-1.5\omega ,1.5\omega )$ is optimal. Hence, we have $P_i=\{[\frac{\omega }{2},1-1.5\omega ],[1.5\omega ,1-\frac{\omega }{2}\}$. In this model, maximizing utility is equivalent to choosing the position where you share as little clients as possible with other agents. If the attraction interval is large enough, then a rational agent will always attract clients near the middle of the line, no matter what he chooses. Hence, an agent will always be better off not choosing a position near the middle of the line.

Lastly, for an even number of agents and $\frac{1}{2}< \omega < 1$, there does not exist a point belief of agent i in $[\frac{\omega }{2},1-\frac{\omega }{2}] \times \cdots \times [\frac{\omega }{2},1-\frac{\omega }{2}]$, such that his choice $c_i \in (\frac{\omega }{2},1-\frac{\omega }{2})$ is optimal. As a result, his point rationalizable choices are $\frac{\omega }{2}$ and $1-\frac{\omega }{2}$.

The iterative procedure to characterize the point rationalizable choices only runs for 1 iteration when we have an odd number of agents and at most 2 rounds for an even number of agents. For both an odd and an even number of agents, the set of point rationalizable choices of an agent i is decreasing in $\omega$, but is not increasing in the number of agents, which was the case for the original Hotelling–Downs model in Sect. 3.

Fig. 5

Point rationalizable choices when $\omega = \frac{4}{15} < \frac{1}{3}$

5 Discussion and conclusion

This paper characterized the point rationalizable choices of the original Hotelling–Downs model for any number of agents. We observed that as the number of agents increases, the set of point rationalizable choices also increases. Consider for example the classical Hotelling beach. The minimum differentiation result only holds when there are two agents in the model, but is not necessarily true when there are more than two agents. However, the socially optimal solution is also not possible if each agent makes a point rationalizable choice. From a social viewpoint, when there are three agents, it would be best if one agent positions at $\frac{1}{6}$, one agent at $\frac{1}{2}$, and one agent at $\frac{5}{6}$. However, the choices $\frac{1}{6}$ and $\frac{5}{6}$ are not point rationalizable. This result is also true for N agents. The socially optimal solution would be where each agent chooses an untaken position in $\left\{ \frac{1}{2N},\frac{3}{2N},\ldots ,\frac{2N-1}{2N}\right\}$. The set of point rationalizable choices is given by $\left[ \frac{1}{2N-2},\frac{2N-3}{2N-2}\right]$, so the choices $\frac{1}{2N}$ and $\frac{2N-1}{2N}$ are not point rationalizable.

We also characterized the set of point rationalizable choices in the Hotelling–Downs model with limited attraction. The set of point rationalizable choices mainly depends on the size of the attraction interval and whether the number of agents in the game is odd or even. For any number of agents, as the size of the attraction interval increases, choosing positions towards the extremes of the line get less attractive.

The reader might wonder why point rationalizability is used as a solution concept instead of rationalizability, which allows for probabilistic beliefs. A characterisation of the set of rationalizable choices for more than two agents turned out to be intractable to solve. With two agents we can show that if $k \le \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$, then in each round $P_i(k)$, the choice $k\delta$ is strictly dominated by the choice $(k+1)\delta$. With three agents or more, this is no longer true. If a choice $c_i$ strictly dominates some other choice $c_i'$, then $c_i$ yields a greater utility to agent i than $c_i'$ for any probabilistic belief about his opponents. Hence, for two agents, the set of rationalizable choices of an agent is the same as his set of point rationalizable choices. For three or more agents, to eliminate a choice $k\delta$ of agent i, this choice must be strictly dominated by some randomization over his (surviving) set of choices $\{k \delta ,\ldots ,1-k\delta \}$. Possibly because of the discontinuity of the utility function of each agent, this turned out to be too difficult to solve for three or more agents. The set of rationalizable choices of an agent is at least as large as his set of point rationalizable choices. This is because in each round of the iterative procedure for rationalizable choices, less or an equal number of choices is eliminated for each agent, compared to the iterative procedure for point rationalizable choices. Furthermore, for three agents, Osborne and Pitchik (1986) find an asymmetric mixed Nash equilibrium where two out of three agents assign strictly positive probability weight to all choices in $\left[ \frac{5}{24},\frac{19}{24}\right]$. This suggests that at least all positions in $\left[ \frac{5}{24},\frac{19}{24}\right]$ are rationalizable.

One of the assumptions that has been made throughout this paper is that clients are uniformly distributed. For some applications, such as voter distributions in a country, this might not be a realistic assumption. It would be interesting to find a characterization of the point rationalizable choices in the original Hotelling–Downs model, but with a more arbitrary distribution of the clients. Similarly, in the Hotelling–Downs model with limited attraction, we assumed that each agent has an attraction region given by $\omega$. It would be interesting to see how the results would generalize if each agent has a different attraction region.

Appendix

1.1 Lemmas and definitions used in theorem 1

With two agents, if $k \le \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$, then in each round $P_i(k)$ the choice $k\delta$ is strictly dominated by the choice $(k+1)\delta$. With three agents or more however, this is no longer true. The lemma below does give us an important insight about the set of point rationalizable choices in relation to the iterative procedure.

Lemma 1

Suppose there are $N \ge 2$ agents, then $\forall i\in I$, $P_i(k)$ has the following property:

• $\{k\delta ,\ldots ,1-k\delta \} \subseteq P_i(k)$ if $k \le \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$

Proof

We will prove by induction. The base case is true for round $k=0$ as $\{0,\ldots ,1\} \subseteq P_i(0)=C_i$.

Now assume that $0 \le k < \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$ and assume that $\forall i \in I$, $\{k\delta ,\ldots ,1-k\delta \}\subseteq P_i(k)$. Without loss of generality we will prove that $\{(k+1)\delta ,\ldots ,1 - (k+1)\delta \} \subseteq P_1(k+1)$. The choice $c_1 \in \{(k+1)\delta ,\ldots ,\left\lceil {\frac{1-\delta }{2}}\right\rceil \}$ is optimal for the point belief $b_1$ with $b_1(c_1 - \delta ,\ldots ,c_1 - \delta )=1$. With this belief, $c_1$ is rightmost and $u_1(c_1,b_1)=\frac{2-2c_1+\delta }{2}=1-c_1+\frac{\delta }{2}\ge 1-\frac{1}{2}+\frac{\delta }{2}>\frac{1}{2}$. If agent 1 chooses $c \in \{c_1+\delta ,\ldots ,1\}$, then c is rightmost and $u_1(c,b_1)=\frac{2-c-c_1+\delta }{2}<\frac{2-2c_1+\delta }{2}=u_1(c_1,b_1)$. If agent 1 chooses $c_1-\delta$, then all agents are positioned at $c_1-\delta$ and $u_1(c_1-\delta ,b_1)=\frac{1}{N}<u_1(c_1,b_1)$. If agent 1 chooses $c \in \{0,\ldots ,c_1-2\delta \}$, then c is leftmost and $u_1(c,b_1)=\frac{c+c_1-\delta }{2} \le \frac{2c_1-3\delta }{2}\le \frac{1-3\delta }{2}<\frac{1}{2}<u_1(c_1,b_1)$. Hence, the choice $c_1 \in \{(k+1)\delta ,\ldots ,\left\lceil {\frac{1-\delta }{2}}\right\rceil \}$ is optimal for the point belief $b_1$ with $b_1(c_1 - \delta ,\ldots ,c_1 - \delta )=1$. By symmetry, the choice $c_1 \in \{\left\lfloor {\frac{1+\delta }{2}}\right\rfloor ,\ldots ,1-(k+1)\delta \}$ is optimal for the point belief $b_1$ with $b_1(c_1+\delta ,\ldots ,c_1+\delta )=1$. This proves that $\{ (k+1)\delta ,\ldots , 1-(k+1)\delta \} \subseteq P_1(k+1)$. $\square$

Because there is a finite number of choices for each agent, there exists some integer $k'$ such that $P_i(k)=P_i(k')$ for all $k \ge k'$, $i\in I$. The point rationalizable choices of agent i are exactly those choices in the minimum round $k+1$ such that all choices $c \in P_i(k)$ are optimal in $P_i(k)$ for a point belief over $P_{-i}(k)$. Now consider round 1 of the iterative procedure. Lemma 1 implies that the choices $\{\delta ,\ldots ,1- \delta \}$ are optimal for some point belief. The remaining question is whether the choice 0 is optimal for some point belief, and because of symmetry, the answer for the choice 1 will be the same. Hence, if 0 is optimal in $P_i(0)$ for a point belief over $P_{-i}(0)$, then all choices in $P_i(0)$ are point rationalizable. If 0 is not optimal for any point belief, then 0 and 1 will be eliminated and $P_i(1)=\{\delta ,\ldots ,1- \delta \}$. The choices $\{2\delta ,\ldots ,1- 2\delta \}$ are optimal in $P_i(1)$ for some point belief over $P_{-i}(1)$. Hence, if $P_i(1)=\{\delta ,\ldots ,1- \delta \}$, then the point rationalizable choices of agent i are $\{\delta ,\ldots ,1- \delta \}$ if $\delta$ is optimal in $P_i(1)$ for a point belief over $P_{-i}(1)$. Lemma 1 implies that we can find the exact set of point rationalizable choices by finding the minimum choice x such that x is optimal in $P_i(\frac{1}{\delta } \cdot x)$ for a point belief over $P_{-i}(\frac{1}{\delta } \cdot x)$. The set of point rationalizable choices for each agent i is then $\{x,\ldots ,1-x\}$.

Definition 3

Consider some sets $A_i \subseteq C_i$, for all $i \in I$.

The tuple of sets $(A_1,\ldots ,A_N)$ is a point best response set if $\forall i \in I$, $c_i \in A_i$ implies that there exist a point belief $b_i$ over the set $A_{-i}$ such that $c_i$ is optimal for $b_i$.

The next Lemma is a result from Proposition 3.1 of Bernheim (1984), which states that the set of point rationalizable choices is equivalent to the largest point best response set.

Lemma 2

For every agent i we have that $P_i=\{c_i\in C_i:$ there exists a point best response set $(A_1,\ldots ,A_N)$ with $c_i\in A_i\}$

As a result, the tuple of sets $(P_1,\ldots ,P_N)$ is the largest tuple of sets such that for each agent i it holds that if $c_i \in P_i$, then there exists a point belief in $P_{-i}$ such that $c_i$ is optimal.

For example, consider the case when we have two agents and consider the tuple of sets $(A_1,A_2)=(\{\delta ,\ldots ,1-\delta \},\{0,\ldots ,1\})$. In this case, it is easy to show that for each choice in $c_1 \in A_1$, there exists a point belief over $A_2$ such that $c_1$ is optimal. However, for the choice $0 \in A_2$, there does not exist a point belief in $A_1$ such that 0 is optimal. Hence, the tuple of sets $(A_1,A_2)$ is not a point best response set.

1.2 Proof of theorem 1 with two agents

Proof

We will prove that in each round $k \le \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$ of the iterative procedure, we have $P_1(k)=P_2(k)=\{k\delta ,\ldots ,1 - k \delta \}$. If $k > \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$, then $P_1(k)=P_2(k)=\{\left\lceil {\frac{1-\delta }{2}}\right\rceil ,1-\left\lceil {\frac{1-\delta }{2}}\right\rceil \}$. As a result, the set of point rationalizable is given by $P_1=P_2=\{\left\lceil {\frac{1-\delta }{2}}\right\rceil ,1-\left\lceil {\frac{1-\delta }{2}}\right\rceil \}$.

We start by proving the base case $P_1(1)=P_2(1)= \{ \delta ,\ldots , 1 - \delta \}$. Without loss of generality we take the perspective of agent 1. The choice $\delta$ yields a strictly higher utility than 0 for any point belief over $P_2(0) = C_2$. Consider the point belief $b_1$ with $b_1(0)=1$. Then $u_1(0,b_1)= \frac{1}{2}< \frac{2-\delta -0}{2}=u_1(\delta ,b_1)$. Now consider the point belief $b_1(\delta )=1$. Then $u_1(0,b_1)= \frac{0+\delta }{2}< \frac{1}{2}=u_1(\delta ,b_1)$. Lastly, consider the point belief $b_1$ with $b_1(c)=1$, where $c \in \{2\delta ,\ldots ,1\}$. Then $u_1(0,b_1)= \frac{0+c}{2}< \frac{\delta +c}{2}=u_1(\delta ,b_1)$. Hence, 0 is not optimal for any point belief and by symmetry, the choice 1 is also not optimal for any point belief.

From the proof of Lemma 1, all choices in $\{\delta ,\ldots ,1-\delta \}$ are optimal for a point belief over $P_2(0)$. This proves that $P_1(1)=P_2(1)=\{\delta ,\ldots , 1 - \delta \}$.

Now we assume that $1 \le k < \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$ and $P_1(k)=P_2(k)= \{k \delta ,\ldots ,1-k \delta \}$ and prove that $P_1(k+1)=P_2(k+1)= \{(k+1) \delta ,\ldots ,1-(k+1) \delta \}$. The choice $(k+1) \delta$ yields a strictly higher utility than $k \delta$ for any point belief over $P_2(k)$. Consider the point belief $b_1$ with $b_1(k \delta )=1$. Then $u_1(k \delta ,b_1)= \frac{1}{2}$ and $u_1((k+1) \delta ,b_1)=\frac{2-(k+1) \delta -k \delta }{2}\ge \frac{2-\frac{1}{2}-\frac{1-2\delta }{2}}{2}> \frac{1}{2}=u_1(k \delta ,b_1)$. Next, consider the point belief $b_1$ with $b_1((k+1) \delta )=1$. Then $u_1(k \delta ,b_1)=\frac{k \delta +(k+1) \delta }{2} \le \frac{\frac{1-2\delta }{2}+\frac{1}{2}}{2}<\frac{1}{2}=u_1((k+1) \delta ,b_1)$. Lastly, consider the point belief $b_1$ with $b_1(c)$, where $c \in \{(k+2)\delta ,\ldots ,1-k \delta \}$. Then $u_1(k \delta ,b_1)=\frac{k \delta +c}{2}< \frac{(k+1) \delta +c}{2}= u_1((k+1) \delta ,b_1)$. Hence, the choice $k \delta$ is not optimal for any point belief and because of symmetry, the choice $1-k \delta$ is also not optimal for any point belief.

From the proof of Lemma 1, all choices in $\{(k+1)\delta ,\ldots ,1-(k+1)\delta \}$ are optimal for a point belief over $P_2(k)$. This proves that $P_1(k+1)=P_2(k+1)=\{(k+1)\delta ,\ldots , 1 -(k+1) \delta \}$.

Next let $k = \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil$. Then $P_1(k)=P_2(k)= \{ k\delta ,\ldots ,1- k\delta \}$. If $\frac{1}{\delta }$ is even, then $k= \frac{1}{\delta } \cdot \frac{1}{2}$ and $P_1(k)=P_2(k)= \{ \frac{1}{2}\}$. Because both agents only have one choice remaining, it must be that $P_1(k)=P_2(k)=P_1(k+1)=P_2(k+1)=\{ \frac{1}{2}\}$. If $\frac{1}{\delta }$ is odd, then $k= \frac{1}{\delta } \cdot \frac{1-\delta }{2}$ and $P_1(k)=P_2(k)= \left\{ \frac{1-\delta }{2},1 - \frac{1-\delta }{2}\right\} = \left\{ \frac{1-\delta }{2}, \frac{1+\delta }{2}\right\}$. Consider the point belief $b_1$ with $b_1\left( \frac{1-\delta }{2}\right) =1$. Then $u_1\left( \frac{1-\delta }{2},b_1\right) =\frac{1}{2}$ and $u_1\left( \frac{1+\delta }{2},b_1\right) = \frac{\frac{1-\delta }{2}+\frac{1+\delta }{2}}{2}=\frac{1}{2}$. Similarly for the point belief $b_1(\frac{1+\delta }{2})=1$ we have $u_1\left( \frac{1-\delta }{2},b_1\right) =\frac{1}{2}$ and $u_1\left( \frac{1+\delta }{2},b_1\right) =\frac{1}{2}$. Hence, $P_1(k)=P_2(k)=P_1(k+1)=P_2(k+1)=\left\{ \frac{1-\delta }{2}, \frac{1+\delta }{2}\right\}$. Because no choices are eliminated for both agents in round k, we have that $P_1(k)=P_2(k)= \left\{ \left\lceil {\frac{1-\delta }{2}}\right\rceil , 1- \left\lceil {\frac{1-\delta }{2}}\right\rceil \right\} \text {\ if\ } k \ge \frac{1}{\delta } \cdot \left\lceil {\frac{1-\delta }{2}}\right\rceil .$ $\square$

1.3 Proof of theorem 1 with three agents

Proof

Let $x=\left\lceil {\frac{1-2\delta }{4}}\right\rceil$. We will show that the set $(\{x,\ldots ,1-x\},\{x,\ldots ,1-x\},\{x,\ldots ,1-x\})$ is a point best response set, and by Lemma 1, the choices in $\{x,\ldots ,1-x\}$ are point rationalizable for each agent. Without loss of generality we prove that all choices in $\{x,\ldots ,1-x\}$ are optimal for agent 1 for some point belief over the set $\{x,\ldots ,1-x\}\times \{x,\ldots ,1-x\}$. We assume that $\delta \le \frac{1}{7}$. This ensures that the proof can be read more intuitively. For example, in the proof we use the choice $c \in \{x+2\delta ,\ldots ,1-x-2\delta \}$. Intuitively, we want that $x+2\delta < 1-x - 2\delta$, so the left element in the set is smaller than the right element. We can ensure this by assuming that $\delta \le \frac{1}{7}$.

Consider the belief $b_1$ with $b_1(x+\delta ,1-x-\delta )=1$. Then x is leftmost and $u_1(x,b_1)=\frac{x+x+\delta }{2}=x+\frac{\delta }{2} \ge \frac{1-2\delta }{4}+ \frac{\delta }{2} = \frac{1}{4}$. The choice $c \in \{0,\ldots ,x-\delta \}$ is leftmost and $u_1(c,b_1)=\frac{c+x+\delta }{2}\le \frac{x-\delta +x+\delta }{2}=x < u_1(x,b_1)$. The choice $x+\delta$ is leftmost sharing with agent 2 and $u_1(x+\delta ,b_1)=\frac{x+\delta +1-x-\delta }{4}= \frac{1}{4} \le u_1(x,b_1)$. The choice $c \in \{x+2\delta ,\ldots ,1-x-2\delta \}$ is middle and $u_1(c,b_1)=\frac{1-x-\delta -x-\delta }{2}=\frac{1}{2}-x-\delta \le \frac{1}{2}-\frac{1-2\delta }{4}-\delta =\frac{1-2\delta }{4}< u_1(x,b_1)$. The choice $1-x-\delta$ is rightmost sharing with agent 3 and $u_1(1-x-\delta ,b_1)=\frac{2-(1-x-\delta )-(x+\delta )}{4}=\frac{1}{4} \le u_1(x,b_1)$. The choice $c \in \{1-x,\ldots ,1\}$ is rightmost and $u_1(c,b_1)=\frac{2-c-(1-x-\delta )}{2}\le \frac{2-(1-x)-(1-x-\delta )}{2}= \frac{2x+\delta }{2}=u_1(x,b_1)$. Hence, the choice x is optimal for agent 1 for belief $b_1$ with $b_1(x+\delta ,1-x-\delta )=1$ and by symmetry the choice $1-x$ is also optimal for this belief.

From the proof of Lemma 1, all choices in $\{x+\delta ,\ldots ,1-x-\delta \}$ are optimal for a point belief over $\{x,\ldots ,1-x\}\times \{x,\ldots ,1-x\}$.

Let $y=x-\delta =\left\lceil {\frac{1-6\delta }{4}}\right\rceil$. Then $y > 0$, because $\delta \le \frac{1}{7}$. We will prove that $(\{y,\ldots ,1-y\},\{y,\ldots ,1-y\},\{y,\ldots ,1-y\})$ is not a point best response set. Consider the choice y of agent 1. We will prove that there does not exist a point belief over $\{y,\ldots ,1-y\}\times \{y,\ldots ,1-y\}$ such that y is optimal for agent 1. Consider the belief where agent 2 and 3 both choose y, then agent 1 is better off choosing $y+\delta$ rather than y. Now consider a belief where only agent 2 chooses y as well. If agent 3 is positioned at $y+\delta$, then agent 1 is better off locating at $y+2\delta$. Now assume that agent 3 is positioned at one of the remaining positions L. Agent 1’s payoff can then be written as $\frac{y+L}{4}$. If agent 1 locates between y and L instead, he obtains $\frac{L-y}{2}$. For y to be optimal for agent 1 we need $\frac{y+L}{4} \ge \frac{L-y}{2}$ which implies that $L \le 3y$. If agent 1 chooses L as well he obtains $\frac{2-L-y}{4}$. For y to be optimal we need $\frac{y+L}{4} \ge \frac{2-L-y}{4}$, which implies that $L \ge 1-y$. This leads to $y \ge \frac{1}{4}$, but we know that $y=\left\lceil {\frac{1-6\delta }{4}}\right\rceil < \frac{1}{4}$. As a result, there is no point belief that contains y such that y is optimal for agent 1.

From now on, we will assume that agent 1’s belief does not contain the position y. If the belief does not contain at least one agent positioned at $y + \delta$, then agent 1 is better off locating to this position. So without loss of generality, we assume that agent 1 believes that agent 2 is positioned at $y+\delta$. A belief where agent 3 also chooses $y+\delta$ does not work, because locating to $y+2\delta$ is then optimal for agent 1. Hence, agent 1 should believe that agent 3 is positioned to the right of $y+\delta$. Agent 1’s payoff for choosing y is then $\frac{y+y+\delta }{2}=y+\frac{\delta }{2}$. Agent 3’s choice cannot be too close to agent 1. If agent 1 believes that agent 3 is positioned to any position to the left of $1-y-\delta$, agent 1 is better off locating to $1-y-\delta$ and obtaining at least $\frac{2-(1-y-\delta )-(1-y-2\delta )}{2}=\frac{2y+3\delta }{2}=y+\frac{3}{2}\delta$. Consider the belief $b_1$ with $b_1(y+\delta ,1-y-\delta )=1$. Then $u_1(y,b_1)=y+\frac{\delta }{2}=\left\lceil {\frac{1-6\delta }{4}}\right\rceil + \frac{1}{2}\delta \le \frac{1-3\delta }{4}+\frac{1}{2}\delta =\frac{1-\delta }{4}$ and $u_1(y+\delta ,b_1)=\frac{y+\delta +1-y-\delta }{4}=\frac{1}{4}$. Lastly, consider the belief $b_1$ where $b_1(y+\delta ,1-y)=1$. Then $u_1(y,b_1) \le \frac{1-\delta }{4}$ and any choice $c \in \{y+2\delta ,\ldots ,1-y-\delta \}$ yields $u_1(c,b_1)=\frac{1-y-y-\delta }{2}=\frac{1}{2}-y-\frac{\delta }{2}=\frac{1}{2}-\left\lceil {\frac{1-6\delta }{4}}\right\rceil -\frac{1}{2}\delta \ge \frac{1}{2}- \frac{1-3\delta }{4}-\frac{1}{2}\delta = \frac{1+\delta }{4}$. Hence, there does not exist a point belief over $\{y,\ldots ,1-y\}\times \{y,\ldots ,1-y\}$ such that y is optimal for agent 1. By symmetry, a similar result holds for the choice $1-y$. $\square$

1.4 Proof of theorem 1 with four or more agents

Proof

Let $x=\left\lceil {\frac{1-(N-2)\delta }{2N-2}}\right\rceil$. We prove that $(\{x,\ldots ,1-x\},\ldots ,\{x,\ldots ,1-x\})$ is a point best response set. Hence, by Lemma 1, the choices in $\{x,\ldots ,1-x\}$ are point rationalizable for each agent. Without loss of generality we prove that all choices in $\{x,\ldots ,1-x\}$ are optimal for agent 1 for some point belief over the set $\{x,\ldots ,1-x\}\times \cdots \times \{x,\ldots ,1-x\}$. Consider the belief $b_1$ with $b_1(c_2,\ldots ,c_N)=1$ where $c_2=x+\delta$, $c_N=1-x-\delta$ and for $j \in \{3,\ldots ,N-1\}$, $c_j=(2j-3)x+(j-2)\delta$. With this belief, x is leftmost and $u_1(x,b_1)=\frac{x+x+\delta }{2}=x+\frac{1}{2}\delta \ge \frac{1+(2-N)\delta }{(2N-2)}+\frac{1}{2}\delta =\frac{4+4\delta }{4(2N-2)}$. The choice $c \in \{0,\ldots ,x-\delta \}$ is leftmost with $u_1(c,b_1)= \frac{c+x+\delta }{2}\le \frac{x-\delta +x+\delta }{2}=\frac{2x}{2}< x+\frac{1}{2}\delta =u_1(x,b_1)$. The choice $c_2=x+\delta$ is leftmost sharing with agent 2. If agent 1 would position at $c_2$, he obtains $u_1(c_2,b_1)=\frac{x+\delta +3x +\delta }{4}=\frac{4x+2\delta }{4}=x+\frac{1}{2}\delta =u_1(x,b_1)$.

For all agents $j \in \{3,\ldots ,N-1\}$, the distance between $c_j$ and $c_{j-1}$ is $2x +\delta$, except for between $c_2$ and $c_3$, for which the distance is 2x. Consider the choices in $c \in \{c_2 +\delta ,\ldots ,c_3-\delta ,c_3+\delta ,\ldots ,c_{N-1}-\delta \}$. This set includes all choices in between $c_2$ and $c_{N-1}$, except the choice(s) $c_k$, where $k \in \{3,\ldots ,N-2\}$. This case has been dealt with separately. The reason for this is that if agent 1 chooses c, he will be the only agent at this position, whereas if agent 1 would choose $c_k$ he will have to share his position with another agent. The choice c is middle and in between $c_j$ and $c_{j-1}$, where $j \in \{3,\ldots ,N-1\}$. The payoff is $u_1(c,b_1)=\frac{c_j - c_{j-1}}{2} \le \frac{2x+\delta }{2}=x+\frac{1}{2}\delta =u_1(x,b_1)$. Now consider a choice positioned at $c_k= (2k-3)x+(k-2)\delta$, where $k \in \{3,\ldots ,N-2\}$. Then $c_k$ is middle sharing with agent k and $u_1(c_k,b_1)=\frac{c_{k+1}-c_{k-1}}{4}\le \frac{(2k-1)x+(k-1)\delta -(2k-5)x-(k-3)\delta }{4}=\frac{4x+2\delta }{4}=x+\frac{1}{2}\delta =u_1(x,b_1)$.

Consider the choice $c_{N-1}= (2N-5)x + (N-3)\delta$. This choice is middle sharing with agent $N-1$ and $u_1(c_{N-1},b_1)=\frac{c_N-c_{N-2}}{4}=\frac{1-x -\delta - (2N-7)x-(N-4)\delta }{4}=\frac{1-(2N-6)x-(N-3)\delta }{4}\le \frac{1+(6-2N)(\frac{1+(2-N)\delta }{2N-2})+(3-N)\delta }{4}$. This can be rewritten to $\frac{4-(2N-6)\delta }{4(2N-2)} < \frac{4+4\delta }{4(2N-2)} \le u_1(x,b_1)$

Consider a choice $c \in \{c_{N-1}+\delta ,\ldots ,c_N - \delta \}$. This choice is middle and $u_1(c,b_1)=\frac{c_N-c_{N-1}}{2}=\frac{1-x-\delta -(2N-5)x-(N-3)\delta }{2}=\frac{1+(4-2N)x+(2-N)\delta }{2}\le \frac{1+(4-2N)(\frac{1-(N-2)\delta }{(2N-2)})+(2-N)\delta }{2}$. This can be rewritten to $\frac{4-(4N-8)\delta }{4}< \frac{4+4\delta }{4(2N-2)} \le u_1(x,b_1)$

Consider the choice $c_N= 1-x-\delta$. This choice is rightmost sharing with agent N and $u_1(c_N,b_1)=\frac{2-(1-x-\delta )-c_{N-1}}{4}=\frac{1+x+\delta -(2N-5)x-(N-3)\delta }{4}=\frac{1+(6-2N)x+(4-N)\delta }{4}\le \frac{1+(6-2N)(\frac{1-(N-2)\delta }{(2N-2)})+(4-N)\delta }{4}$. This can be rewritten to $\frac{4+4\delta }{4(2N-2)} \le u_1(x,b_1)$

Lastly, consider the choice $c \in \{c_N + \delta ,\ldots ,1\}$. Then c is rightmost and $u_1(c,b_1)=\frac{2-c-c_N}{2}\le \frac{2-(c_N +\delta )- c_N}{2}=\frac{2-2c_N-\delta }{2}=\frac{2-2(1-x-\delta )-\delta }{2}=\frac{2x+\delta }{2}=u_1(x,b_1)$.

Hence, the choice x is optimal for agent 1 for belief $b_1$ with $b_1(c_2,\ldots ,c_N)=1$ and by symmetry, the choice $1-x$ is also optimal for this belief. From the proof of Lemma 1, all choices in $\{x+\delta ,\ldots ,1-x-\delta \}$ are optimal for a point belief over $\{x,\ldots ,1-x\}\times ... \times \{x,\ldots ,1-x\}$. As a result, we have that $(\{x,\ldots ,1-x\},\ldots ,\{x,\ldots ,1-x\})$ is a point best response set.

Let $y=x-\delta =\left\lceil {\frac{1-(N-2)\delta }{(2N-2)}}\right\rceil - \frac{(2N-2)\delta }{(2N-2)}=\left\lceil {\frac{1-(3N-4)\delta }{(2N-2)}}\right\rceil$. The condition $\delta < \frac{1}{3(N-3)+6}$ is needed to ensure that $y > 0$. If $y=0$, then the proof is no longer valid. Point beliefs about the choices of the opponents we will label such as $c_2=y+\delta$ and $c_3=3y+\delta$ would then be the same choice, which is not what is meant in the proof.

We will prove that $(\{y,\ldots ,1-y\},\ldots ,\{y,\ldots ,1-y\})$ is not a point best response set by showing that y is not optimal for agent 1 for any point belief over $\{y,\ldots ,1-y\} \times \cdots \times \{y,\ldots ,1-y\}$. For the point belief $b_1$ where $b_1(y,\ldots ,y)=1$, agent 1 is better off locating to $y+\delta$. Hence, for the remainder of the proof agent 1 assumes that at least one agent is not positioned at y. We will denote the belief of agent 1 about an individual opponent’s choice as $c_j$, where $j\in \{2,\ldots ,N\}$. Because of symmetry, we can assume that $c_2 \le c_3 \le \cdots \le c_N$. Let L denote the closest agent to agent 1, but not at y. Because y is a leftmost choice for any point belief, the payoff of agent 1 can be denoted as $\frac{y+L}{2D_1(y,c_{-1})}$. Hence, for higher values of y the payoff for agent 1 increases, which makes deviating to a different choice less attractive. If the distance between some other agents is too large, agent 1 can position between these agents to obtain a better payoff. Similarly, if all the agents are positioned too closely to each other, there will exist a “gap” on the line where agent 1 can deviate to. Between each agent there will be a maximum distance such that agent 1 does not want to deviate from his original choice y. We will show that even if we maximize the space between all agents given the constraints that we have, there is still too much space at the end of the line. This results in a higher payoff for agent 1 if he deviates to a certain position at the end of the line. We will also show that the main reason for this is because y is not large enough.

Assume that agent 1 believes that there is exactly one other agent positioned at y as well. This implies that $c_2=y$. The payoff of agent 1 then depends on the position of the closest agent to y, which is $c_3$. The payoff of agent 1 is thus equal to $\frac{y+c_3}{4}$. If agent 1 would locate in between y and $c_3$, his payoff is equal to $\frac{c_3-y}{2}$. Hence, $\frac{y+c_3}{4} \ge \frac{c_3-y}{2}$ which implies $c_3 \le 3y$. To maximize the distance between agent 1 and agent 3, agent 1 believes that agent 3 is positioned at 3y. agent 1’s payoff is then equal to $\frac{y+3y}{4}=y$. Now let L be the closest agent to the right of 3y. agent 1’s payoff for choosing 3y is equal to $\frac{L-y}{2D_1(3y,c_{-1})}$. Note that $D_1(3y,c_{-1})=2$ when only agent 1 and 3 are positioned at 3y. If additional agents are also positioned at 3y, then $D_1(3y,c_{-1})>2$. Hence, $y \ge \frac{L-y}{2D_1(3y,c_{-1})}$ which implies $L \le (2D_1(3y,c_{-1})+1)y$. If $D_1(3y,c_{-1})=2$, this simplifies to $L \le 5y$. If additional agents are positioned at 3y, then the right term of the constraint will increase as well. For example, if agent 1 and 3 and 4 are positioned at 3y, the constraint simplifies to $L \le 7y$. However, even if additional agents are positioned at 3y, when agent 1 chooses a position in between 3y and L, it leads to $y \ge \frac{L-3y}{2}$ which implies that $L \le 5y$. Hence, if additional agents are positioned at 3y, it leads to the same maximum choice where L can be positioned. Furthermore, additional agents at 3y implies that there are less agents in total to use to maximize the distance between the agents. Hence, $c_4=5y$.

Fig. 6

Feasible region when agent 2 is also positioned at y

This pattern continues and we find that for $j \in \{3, \ldots , N-1\}, c_j=(2j-3)y$. agent 3 until agent $N-1$ are spread out in a manner such that the distance is maximized between the agents and agent 1 has no incentive to deviate to any position in $\{y+\delta ,\ldots ,c_{N-1}-\delta \}$. If agent 1 would locate at $c_{N}$, his payoff is equal to $\frac{2-c_N-c_{N-1}}{4}=\frac{2-c_N - (2N-5)y}{4}$. Hence, $y \ge \frac{2-c_N - (2N-5)y}{4}$ which implies that $c_N \ge 2-(2N-1)y$. Note that at least one agent should locate at $1-y-\delta$ or $1-y$, because otherwise agent 1 can deviate to $1-y-\delta$ and obtain a higher payoff of at least $\frac{2- (1-y-\delta ) -(1-y-2\delta )}{2}= y+ \frac{3}{2}\delta > y$. Hence, we have $c_N \ge 1-y-\delta$ and $c_N \ge 2-(2N-1)y$. We are interested in the minimum value of y such that both constraints are satisfied. Figure 6 plots the two constraints. The arrows represent the direction in which each constraint is satisfied. From the figure it is clear that the minimum value of y for which both constraints are satisfied is exactly when the lines intersect. The lines intersect when $y=\frac{1+\delta }{2N-2}$. This might not be a position on the line, so the minimum permitted value is given by $y = \left\lceil {\frac{1+\delta }{2N-2}}\right\rceil$. However, we have that $y=\left\lceil {\frac{1-(3N-4)\delta }{2N-2}}\right\rceil < \left\lceil {\frac{1+\delta }{2N-2}}\right\rceil$. Hence, a point belief where one other agent is also positioned at y does not lead to y being optimal for agent 1. A point belief where additional agents are positioned at y also does not lead to y being optimal for agent 1. The payoff of agent 1 is then $\frac{y+L}{2D_1(y,c_{-1})} < \frac{y+L}{4}$, which means that deviating from y is more attractive and leads to the condition that agents need to be positioned even closer to each other. Furthermore, there is at least one less agent to the right of y, which cannot be used for maximizing the space between the agents. As a result, a point belief of agent 1 that contains the choice y does not lead to y being optimal for agent 1.

From now on, we assume that the point belief of agent 1 does not contain y. If none of the agents locate at $y+\delta$, agent 1 is better off locating to $y + \delta$, so without loss of generality agent 1 believes that $c_2=y + \delta$. The payoff of agent 1 is then equal to $\frac{y+c_2}{2}=\frac{y+y+\delta }{2}=y+\frac{1}{2}\delta$.

If agent 1 would choose to locate at $c_2$ instead, the payoff it will receive depends on how many agents are positioned at $c_2$ and the position of the closest agent to the right of $c_2$. We will call this position L. Deviating to $c_2$ leads to a payoff of $\frac{y+\delta +L}{2D_1(c_2,c_{-1})}$ for agent 1. We have that $D_1(c_2,c_{-1})=2$ when only agent 1 and 2 are positioned on $c_2$. If additional agents are also positioned on $c_2$, then $D_1(c_2,c_{-1})>2$. Hence, $y + \frac{1}{2}\delta \ge \frac{y+\delta +L}{2D_1(c_2,c_{-1})}$ which implies $L \le 2D_1(c_2,c_{-1})(y+\frac{1}{2}\delta )-y-\delta$. If $D_1(c_2,c_{-1})=2$, this simplifies to $L \le 3y+\delta$. If $D_1(c_2,c_{-1})>2$, then the right term of the constraint will increase with $2y+\delta$ for each additional agent. If agent 1 would deviate to $c \in \{y +2\delta ,\ldots ,L-\delta \}$ it leads to a payoff of $\frac{L-c_2}{2}=\frac{L - y -\delta }{2}$ for agent 1. Hence, $y +\frac{1}{2}\delta \ge \frac{L - y -\delta }{2}$ which implies $L \le 3y +2\delta$. We thus have the two constraints $L \le 2D_1(c_2,c_{-1})(y+\frac{1}{2}\delta )-y-\delta$ and $L \le 3y +2\delta$. Which constraint is the stricter one depends on the value of $D_1(c_2,c_{-1})$.

If $D_1(c_2,c_{-1})=2$, then only agent 1 and 2 are positioned at $c_2$ and the first constraint simplifies to $L \le 3y+\delta$. This is a stricter constraint than the other constraint of $L \le 3y +2\delta$. To maximize the distance between the agents, we have $c_3=3y+\delta$. The agent closest to the right of $c_3=3y+\delta$ is now labeled L. The payoff of agent 1 for locating to $c_3$ is then equal to $\frac{L-c_2}{2D_1(c_3,c_{-1})}=\frac{L-y-\delta }{2D_1(c_3,c_{-1})}$. Hence, $y+ \frac{1}{2}\delta \ge \frac{L-y-\delta }{2D_1(c_3,c_{-1})}$ which implies $L \le 2D_1(c_3,c_{-1})(y+\frac{1}{2}\delta )+y+\delta$. If $D_1(c_3,c_{-1})=2$, then only agent 1 and 3 are positioned at $c_3$ and the constraint simplifies to $L \le 5y+3\delta$. If $D_1(c_3,c_{-1})>2$, then the right term of the constraint will increase with $2y+\delta$ for each additional agent. The payoff for agent 1 of locating to $c \in \{c_3+\delta ,\ldots ,L-\delta \}$ is $\frac{L-3y-\delta }{2}$. Hence, $y+\frac{1}{2}\delta \ge \frac{L-3y-\delta }{2}$ which implies $L \le 5y + 2\delta$. Regardless of how many agents are positioned at $3y+\delta$, the strictest constraint will always be $L \le 5y + 2\delta$ and as a result $c_4=5y+2\delta$.

If $D_1(c_2,c_{-1})>2$, then there is at least one additional agent positioned at $c_2$, which implies $c_3=y+\delta =c_2$. Agent 1 will not choose deviate to position $c_2=c_3$ if $L \le 2D_1(c_2,c_{-1})(y+\frac{1}{2}\delta )-y-\delta$, which will be at least $5y+2\delta$, because $D_1(c_2,c_{-1})>2$. Similarly, agent 1 will not deviate to a position in $\{y+2\delta ,\ldots ,L-\delta \}$ if $L\le 3y +2\delta$. Note that if there is more than one additional agent, the strictest constraint is still $L\le 3y +2\delta$. To maximize the distance between the agents, we have that $c_4=3y+2\delta$.

The assumption that $D_1(c_2,c_{-1})=2$ results in $c_3=3y+\delta$ and $c_4=5y+2\delta$, while $D_1(c_2,c_{-1})>2$ results in $c_2=c_3=y+\delta$ and $c_4=3y+2\delta$. Because $D_1(c_2,c_{-1})=2$ is better at maximizing the space between the agents, we will further explore this assumption.

From agent 3 on wards until agent $N-1$ we let the distance between agents be equal to $2y+\delta$. As such, agent 1 has no incentive to choose any position in $\{y+\delta ,\ldots ,c_{N-1}-\delta \}$. Hence, this way the space between the agents is maximized and we can now check if there is too much space at the end of the line. Similar to the constraints that led to Fig. 6, Fig. 7 denotes the corresponding constraints $c_N \ge 2- (2N-1)y-(N-1)\delta$ and $c_N \ge 1-y - \delta$, which leads to $y = \left\lceil {\frac{1-(N-2)\delta }{2N-2}}\right\rceil =x$. However, we have $y= x- \delta$, so a point belief where no agent is positioned at y also does not lead to y being optimal for agent 1. To conclude, there is no point belief over $\{y,\ldots ,1-y\} \times \cdots \times \{y,\ldots ,1-y\}$ such that y is optimal. By symmetry, a similar result holds for the choice $1-y$. $\square$

Fig. 7

Feasible region when no other agent chooses y

1.5 Lemmas and observations used for theorem 2

Lemma 3

Consider agent i and two choices $c_i$ and $c_i'$, where $c_i,c_i' \in [\frac{\omega }{2},1-\frac{\omega }{2}]$, $c_i < c_i'$ and $c_i'- c_i < \omega$. Choosing $c_i$ yields a greater utility to agent i than choosing $c_i'$ if and only if

$$\begin{aligned} \int _{c_i-\frac{\omega }{2}}^{c_i'-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x > \int _{c_i+\frac{\omega }{2}}^{c_i'+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x. \end{aligned}$$

Similarly, choosing $c_i$ yields a lower utility than $c_i'$ if and only if

$$\begin{aligned} \int _{c_i-\frac{\omega }{2}}^{c_i'-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x < \int _{c_i+\frac{\omega }{2}}^{c_i'+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x. \end{aligned}$$

Proof

Choosing $c_i$ yields a greater utility to agent i than choosing $c_i'$ if and only if

$$\begin{aligned} \int _{c_i-\frac{\omega }{2}}^{c_i+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x > \int _{c_i'-\frac{\omega }{2}}^{c_i'+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x \, \end{aligned}$$

which means that

$$\begin{aligned} \int _{c_i-\frac{\omega }{2}}^{c_i'-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x + \int _{c_i'-\frac{\omega }{2}}^{c_i + \frac{\omega }{2}} a_{x,i} \,\textrm{d}x > \int _{c_i'-\frac{\omega }{2}}^{c_i+ \frac{\omega }{2}} a_{x,i} \,\textrm{d}x \int _{c_i+\frac{\omega }{2}}^{c_i'+ \frac{\omega }{2}} a_{x,i} \,\textrm{d}x \, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \int _{c_i-\frac{\omega }{2}}^{c_i'-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x > \int _{c_i+\frac{\omega }{2}}^{c_i'+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x. \end{aligned}$$

$\square$

Observation 1

Consider an agent i and let $0 < \omega \le 1$. If $x,x'\in [0,\frac{\omega }{2}]$ and $x < x'$, then $|I_x|\le |I_{x'}|$. Similarly, if $x,x'\in [1-\frac{\omega }{2},1]$ and $x < x'$, then $|I_x|\ge |I_{x'}|$.

Proof

We will prove the case where $x,x'\in [0,\frac{\omega }{2}]$ and $x < x'$. A client at x will be attracted by agents in between 0 and $x+\frac{\omega }{2}$. A client at $x'$ will be attracted by agents in between 0 and $x'+\frac{\omega }{2}$. Hence, $|I_x|\le |I_{x'}|$. $\square$

Observation 2

Consider agent i and let each opponent agent $j\ne i$ choose $c_j \in \left[ \frac{\omega }{2},1-\frac{\omega }{2}\right]$ and let $0 < \omega \le 1$. If $x,x'\in [0,\omega ]$ and $x < x'$, then $|I_x|\le |I_{x'}|$. Similarly, if $x,x'\in [1-\omega ,1]$ and $x < x'$, then $|I_x|\ge |I_{x'}|$.

Proof

We will prove the case where $x,x'\in [0,\omega ]$ and $x < x'$. A client at x will be attracted by agents in between $\frac{\omega }{2}$ and $x+\frac{\omega }{2}$. A client at $x'$ will be attracted by agents in between $\frac{\omega }{2}$ and $x'+\frac{\omega }{2}$. Hence, $|I_x|\le |I_{x'}|$. $\square$

Lemma 4

Consider agent i and let $0 < \omega \le 1$. Let $a,b,c \in [0,\frac{\omega }{2}]$ and $a<b<c$. Then

$$\begin{aligned} \frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x \ge \frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x. \end{aligned}$$

Similarly, if we let $a,b,c \in [1-\frac{\omega }{2},1]$ and $a<b<c$, then

$$\begin{aligned} \frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x \le \frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x. \end{aligned}$$

Proof

We will prove the case where $a,b,c \in [0,\frac{\omega }{2}]$ and $a<b<c$. By Observation 1, we know that $|I_x|\le |I_{x'}| \forall x \in [a,b]$ and $x'\in [b,c]$. If $|I_x|= |I_{x'}| \forall x,x' \in (a,c)$, then there are exactly $l \in \{0,\ldots ,N-1\}$ opponent agents that attract clients in (a, c). This implies that $\int _{a}^{b} a_{x,i} \,\textrm{d}x=(b-a)\frac{1}{l+1}$ and $\int _{b}^{c} a_{x,i} \,\textrm{d}x=(c-b)\frac{1}{l+1}$ and hence $\frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x= \frac{1}{b-a} \cdot (b-a)\frac{1}{l+1}=\frac{1}{c-b} \cdot (c-b)\frac{1}{l+1}= \frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x$.

Now suppose that $|I_x|< |I_{x'}|$ for some $x \in (a,b]$ and $x'\in [b,c)$, Then $|I_a|< |I_{c}|$. Let $|I_a|=N_1$. Then there exists a position $\beta \in (a,c)$ such that $|I_x|=N_1 \ \forall x\in [a,\beta ]$ and $|I_x|>N_1 \ \forall x\in (\beta ,c]$. We will now consider two cases.

Case 1: Let $\beta \in (a,b)$. Then $|I_b|=N_2 > N_1=|I_a|$, and $|I_x| \le N_2 \ \forall x\in (\beta ,b]$ and $|I_x| \ge N_2 \ \forall x \in [b,c]$. Then $\frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x \ge \frac{1}{b-a} \cdot ((\beta -a)\cdot \frac{1}{N_1+1} + (b-\beta )\cdot \frac{1}{N_2+1}) > \frac{1}{b-a} \cdot ((\beta -a)\cdot \frac{1}{N_2+1} + (b-\beta )\cdot \frac{1}{N_2+1}) = \frac{1}{N_2+1}$, whereas $\frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x \le \frac{1}{c-b} ((c-b)\frac{1}{N_2+1})=\frac{1}{N_2+1}$.

Case 2: Let $\beta \in [b,c)$. Then $|I_b|=|I_a|=N_1$, $|I_x|=N_1 \ \forall x \in [b,\beta ]$ and $|I_x|>N_1 \ \forall x \in (\beta ,c]$. Then $\frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x= \frac{1}{b-a} \cdot ((b-a)\cdot \frac{1}{N_1+1})=\frac{1}{N_1+1}$, whereas $\frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x < \frac{1}{c-b}((\beta -b)\cdot \frac{1}{N_1+1}+(c-\beta )\cdot \frac{1}{N_1+1})=\frac{1}{N_1+1}$.

Finally, we can conclude that if $|I_x|< |I_{x'}|$ for some $x \in (a,b]$ and $x'\in [b,c)$, then $\frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x > \frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x$. $\square$

Lemma 5

Consider agent i and let each opponent agent $j\ne i$ choose $c_j \in \left[ \frac{\omega }{2},1-\frac{\omega }{2}\right]$ and let $0 < \omega \le 1$. Let $a,b,c \in [0,\omega ]$ and $a<b<c$. Then

$$\begin{aligned} \frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x \ge \frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x. \end{aligned}$$

Similarly, if we let $a,b,c \in [1-\omega ,1]$ and $a<b<c$, then

$$\begin{aligned} \frac{1}{b-a} \cdot \int _{a}^{b} a_{x,i} \,\textrm{d}x \le \frac{1}{c-b} \cdot \int _{b}^{c} a_{x,i} \,\textrm{d}x. \end{aligned}$$

Proof

Similar to the proof of Lemma 4. $\square$

1.6 Proof of theorem 2 for an odd number of agents

Proof

Consider an agent $i \in I$. We start by showing that $c_i \in [0,\frac{\omega }{2})$ is not optimal for any point belief. Choosing $\frac{\omega }{2}$ yields agent $i \int _{0}^{\omega } a_{x,i} f(x) \, \textrm{d}x= \int _{0}^{\omega } a_{x,i} \, \textrm{d}x$, whereas choosing $c_i\in [0,\frac{\omega }{2})$ yields agent i $\int _{c_i-\frac{\omega }{2}}^{c_i+\frac{\omega }{2}} a_{x,i} f(x) \, \textrm{d}x=\int _{0}^{c_i+\frac{\omega }{2}} a_{x,i} \, \textrm{d}x < \int _{0}^{c_i+\frac{\omega }{2}} a_{x,i} \, \textrm{d}x + \int _{c_i+\frac{\omega }{2}}^{\omega } a_{x,i} \, \textrm{d}x = \int _{0}^{\omega } a_{x,i}\, \textrm{d}x$. Hence, $\frac{\omega }{2}$ strictly dominates the choices in $[0,\frac{\omega }{2})$. Similarly, $1- \frac{\omega }{2}$ strictly dominates the choices in $(1-\frac{\omega }{2},1]$. As a result, all choices in $(1-\frac{\omega }{2},1]$ are not optimal for any point belief.

First, let $0 < \omega \le \frac{1}{3}$ and consider an agent i. The choice $c_i\in [\frac{\omega }{2},\frac{1}{2}]$ is optimal for the belief $b_i$ with $b_i(1-\frac{\omega }{2},\ldots ,1-\frac{\omega }{2})=1$. Since $\omega \le \frac{1}{3}$, we have that $c_i+\frac{\omega }{2} \le \frac{1}{2}+\frac{\omega }{2} \le 1-\omega$. Hence, all clients in between $c_i - \frac{\omega }{2}$ and $c_i + \frac{\omega }{2}$ are only attracted to agent i. Thus, $c_i$ is optimal. Similarly, the choice $c_i\in [\frac{1}{2},1-\frac{\omega }{2}]$ is optimal for the belief $b_i$ with $b_i(\frac{\omega }{2},\ldots ,\frac{\omega }{2})=1$.

Next, let $\frac{1}{3} < \omega \le \frac{1}{2}$. Consider the choice $c_i \in [\frac{\omega }{2},1-1.5\omega ]$ and the belief $b_i$ with $b_i(1-\frac{\omega }{2},\ldots ,1-\frac{\omega }{2})=1$. Since $c_i +\frac{\omega }{2} \le 1- \omega$, all clients in between $c_i - \frac{\omega }{2}$ and $c_i + \frac{\omega }{2}$ are only attracted to agent i. Hence, $c_i$ is optimal. Note that $\omega \le \frac{1}{2}$ ensures that $\frac{\omega }{2} \le 1-1.5\omega$. Similarly, the choice $c_i \in [1.5\omega ,1-\frac{\omega }{2}]$ is optimal for the belief $b_i$ with $b_i(\frac{\omega }{2},\ldots ,\frac{\omega }{2})=1$. The choice $c_i \in [1-1.5\omega , 1.5 \omega ]$ is optimal for the point belief where $k=\frac{N-1}{2}$ agents are positioned at $\frac{\omega }{2}$ and k agents are positioned at $1- \frac{\omega }{2}$. For this point belief, $|I_x|= k \ \forall x\in [0,\omega ]$, $|I_x|=0 \ \forall x\in [\omega ,1-\omega ]$, and $|I_x|= k \ \forall x\in [1-\omega ,1]$. Then $c_i$ is optimal if it attracts all clients in between $\omega$ and $1-\omega$. As $c_i \in (1-1.5\omega ,1.5\omega )$, we have that $c_i-\frac{\omega }{2} < \omega$ and $c_i+\frac{\omega }{2} > 1-\omega$. Hence, $c_i$ is optimal for the point belief above.

Lastly, let $\frac{1}{2} < \omega \le 1$. Then the choice $c_i \in [\frac{\omega }{2},1-\frac{\omega }{2}]$ is optimal for the point belief $b_i$ such that $k=\frac{N-1}{2}$ opponents are positioned at $\frac{\omega }{2}$ and k opponents are positioned at $1-\frac{\omega }{2}$. Note that for this point belief, $|I_x|= k \ \forall x,\in [0,1-\omega ]$, $|I_x|=2k \ \forall x\in [1-\omega ,\omega ]$, and $|I_x|= k \ \forall x\in [\omega ,1]$. Hence,

$$\begin{aligned} u_i(c_i,b_i)=((1-\omega )-(c_i-\frac{\omega }{2})) \cdot \frac{1}{k+1}+ (\omega - (1-\omega ))\cdot \frac{1}{2k+1}+ (c_i+\frac{\omega }{2}-\omega ) \cdot \frac{1}{k+1}, \end{aligned}$$

which simplifies to

$$\begin{aligned} (1-\omega ) \cdot \frac{1}{k+1} + (2\omega -1) \cdot \frac{1}{2k+1}. \end{aligned}$$

Hence, the choice $c_i$ is optimal for the point belief described above.

We have shown that $P_i(1)= [\frac{\omega }{2},1-\frac{\omega }{2}] \ \forall i \in \{1,2,\ldots ,N\}$. Because for each agent i, the choice $c_i \in P_i(1)$ is optimal for a point belief in $P_{-i}(1)$, the procedure terminates after round 1 and we conclude that $P_i= [\frac{\omega }{2},1-\frac{\omega }{2}] \ \forall i \in \{1,2,\ldots ,N\}$. $\square$

1.7 Proof of theorem 2 for an even number of agents

Proof

Similar to the case with an odd number of agents and $0 < \omega \le 1$, we can show all choices in $[0,\frac{\omega }{2})$ and $(1-\frac{\omega }{2},1]$ are not optimal for any point belief.

Let $0 < \omega \le \frac{1}{3}$. Also similarly to the proof of the case with an odd number of agents, the choice $c_i\in [\frac{\omega }{2},\frac{1}{2}]$ is optimal for the belief $b_i$ with $b_i(1-\frac{\omega }{2},\ldots ,1-\frac{\omega }{2})=1$. Similarly, the choice $c_i\in [\frac{1}{2},1-\frac{\omega }{2}]$ is optimal for the belief $b_i$ with $b_i(\frac{\omega }{2},\ldots ,\frac{\omega }{2})=1$. Hence, $P_i(1)=[\frac{\omega }{2},1-\frac{\omega }{2}]$. Because for each agent i, the choice $c_i \in P_i(1)$ is optimal for a point belief in $P_{-i}(1)$, the procedure terminates after round 1 and we conclude that $P_i= [\frac{\omega }{2},1-\frac{\omega }{2}] \ \forall i \in \{1,2,\ldots ,N\}$.

Next, consider $\frac{1}{3} < \omega \le \frac{1}{2}$. Consider the choice $c_i \in [\frac{\omega }{2},\frac{1}{2}]$ and the belief $b_i$ with $b_i(1,\ldots ,1)=1$. Since $\omega \le \frac{1}{2}$, we have that $c_i+\frac{\omega }{2} \le \frac{1}{2}+\frac{\omega }{2} \le 1- \frac{\omega }{2}$. Hence, all clients in between $c_i - \frac{\omega }{2}$ and $c_i + \frac{\omega }{2}$ are only attracted to agent i. Thus, $c_i$ is optimal. Similarly, the choice $c_i\in [\frac{1}{2},1-\frac{\omega }{2}]$ is optimal for the belief $b_i$ with $b_i(0,\ldots ,0)=1$. Hence, $P_i(1)=[\frac{\omega }{2},1-\frac{\omega }{2}] \ \forall i\in \{1,\ldots ,N\}$.

Consider agent i in the next round. Consider the choice $c_i \in [\frac{\omega }{2},1-1.5\omega ]$ and the point belief $b_i$ with $b_i=(1-\frac{\omega }{2},\ldots ,1-\frac{\omega }{2})=1$. Since $\omega \le \frac{1}{2}$, we have that $c_i+\frac{\omega }{2}\le 1-1.5\omega +\frac{\omega }{2} \le 1- \omega$. Hence, all clients in between $c_i - \frac{\omega }{2}$ and $c_i + \frac{\omega }{2}$ are only attracted to agent i. Thus, $c_i$ is optimal. Similarly, the choice $c_i \in [1.5\omega ,1-\frac{\omega }{2}]$ is optimal for the belief $b_i$ with $b_i=(\frac{\omega }{2},\ldots ,\frac{\omega }{2})=1$. Suppose by contradiction that $c_i \in (1-1.5\omega ,1.5\omega )$ is optimal for some point belief. Choosing $c_i$ should yield at least as much as choosing $1-1.5\omega$. Lemma 3 then implies

$$\begin{aligned} \int _{1-\omega }^{c_i+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x \ge \int _{1-2\omega }^{c_i-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x. \end{aligned}$$

(1)

Choosing $c_i$ should also yield at least as much as choosing $1.5\omega$. Lemma 3 then implies

$$\begin{aligned} \int _{c_i-\frac{\omega }{2}}^{\omega } a_{x,i} \,\textrm{d}x \ge \int _{c_i+\frac{\omega }{2}}^{2\omega } a_{x,i} \,\textrm{d}x. \end{aligned}$$

(2)

Furthermore, Lemma 5 implies

$$\begin{aligned} \frac{1}{c_i+1.5\omega -1} \int _{1-2\omega }^{c_i-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x \ge \frac{1}{1.5 \omega -c_i} \int _{c_i-\frac{\omega }{2}}^{\omega } a_{x,i} \,\textrm{d}x. \end{aligned}$$

(3)

Similarly, Lemma 5 implies

$$\begin{aligned} \frac{1}{c_i+1.5\omega -1} \int _{1-\omega }^{c_i+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x \le \frac{1}{1.5 \omega -c_i} \int _{c_i+\frac{\omega }{2}}^{2\omega } a_{x,i} \,\textrm{d}x. \end{aligned}$$

(4)

Combining (2),(3) and (4) implies that

$$\begin{aligned} \begin{aligned}&\frac{1}{c_i+1.5\omega -1} \int _{1-2\omega }^{c_i-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x \ge \frac{1}{1.5 \omega -c_i} \int _{c_i-\frac{\omega }{2}}^{\omega } a_{x,i} \,\textrm{d}x \\ \ge&\frac{1}{1.5 \omega -c_i} \int _{c_i+\frac{\omega }{2}}^{2\omega } a_{x,i} \,\textrm{d}x \ge \frac{1}{c_i+1.5\omega -1} \int _{1-\omega }^{c_i+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x. \end{aligned} \end{aligned}$$

(5)

Then (1) and (5) imply

$$\begin{aligned} \begin{aligned}&\frac{1}{c_i+1.5\omega -1} \int _{1-2\omega }^{c_i-\frac{\omega }{2}} a_{x,i} \,\textrm{d}x = \frac{1}{1.5 \omega -c_i} \int _{c_i-\frac{\omega }{2}}^{\omega } a_{x,i} \,\textrm{d}x \\ =&\frac{1}{1.5 \omega -c_i} \int _{c_i+\frac{\omega }{2}}^{2\omega } a_{x,i} \,\textrm{d}x = \frac{1}{c_i+1.5\omega -1} \int _{1-\omega }^{c_i+\frac{\omega }{2}} a_{x,i} \,\textrm{d}x. \end{aligned} \end{aligned}$$

(6)

The proof of Lemma 5 and the first equality in (6) imply that

$$\begin{aligned} |I_x|=|I_{x'}| \ \forall x,x'\in (1-2\omega ,\omega ). \end{aligned}$$

(7)

Similarly, the proof of Lemma 5 and the last equality in (6) implies that

$$\begin{aligned} |I_x|=|I_{x'}| \ \forall x,x'\in (1-\omega ,2\omega ). \end{aligned}$$

(8)

Furthermore, (6) implies that

$$\begin{aligned} |I_x|=|I_{1-x}| \ \forall x \in (1-2\omega ,\omega ) \ \text {and} \ |I_x|=|I_{1-x}| \ \forall x\in (1-\omega ,2\omega ). \end{aligned}$$

(9)

By contradiction, assume that $c_j \in (1-1.5\omega ,1.5\omega )$ for some opponent j. Then this opponent attracts clients in between $c_j-\frac{\omega }{2}$ and $c_j+\frac{\omega }{2}$, where $1-2\omega< c_j-\frac{\omega }{2} < \omega$ and $1-\omega< c_j+\frac{\omega }{2} < 2\omega$. Observation 2 then implies that $|I_{x}|< |I_{x'}| \ \forall x\in [1-2\omega ,c_j-\frac{\omega }{2}) \ \text {and} \ \forall x' \in [c_j-\frac{\omega }{2},\omega ]$. As a result, (7) cannot hold. Similarly, (8) cannot hold. So from now on, we assume that each opponent agent chooses in either $[\frac{\omega }{2},1-1.5\omega ]$ or $[1.5\omega ,1-\frac{\omega }{2}]$.

Note that if an opponent chooses $c_j \in [\frac{\omega }{2},1-1.5\omega ]$, then he will attract all clients in $(1-2\omega ,\omega )$ and none of the clients in $(1-\omega ,2\omega )$. Similarly, if an opponent chooses $c_j \in [1.5\omega ,1-\frac{\omega }{2}]$, then he will attract all clients in $(1-\omega ,2\omega )$ and none of the clients in $(1-2\omega ,\omega )$. Hence, (9) can only hold if an equal number of opponents is positioned in $[\frac{\omega }{2},1-1.5\omega ]$ as in $[1.5\omega ,1-\frac{\omega }{2}]$. As a result, (9) cannot hold if the number of agents is even. We conclude that if the number of agents is even, then for each agent i, $c_i$ is not optimal for any point belief over $P_{-i}(1)$ and $P_i=([\frac{\omega }{2},1-1.5\omega ],[1.5\omega ,1-\frac{\omega }{2}])$.

Next, consider $\frac{1}{2} < \omega \le \frac{2}{3}$. The choice $c_i \in [\frac{\omega }{2},1-\omega ]$ is optimal for the belief $b_i$ with $b_i(1,\ldots ,1)=1$. Note that $\omega \le \frac{2}{3}$ ensures that $\frac{\omega }{2} \le 1-\omega$. Furthermore, we have that $c_i+\frac{\omega }{2} \le 1-\omega +\frac{\omega }{2}=1-\frac{\omega }{2}$. Hence, all clients in between $c_i - \frac{\omega }{2}$ and $c_i + \frac{\omega }{2}$ are only attracted to agent i. Thus, $c_i$ is optimal. Similarly, the choice $c_i \in [\omega ,1-\frac{\omega }{2}]$ is optimal for the belief $b_i$ with $b_i=(0,\ldots ,0)$. Similarly to the previous case where $\frac{1}{3} < \omega \le \frac{1}{2}$, we can show that $c_i \in (1-\omega ,\omega )$ is not optimal for any point belief. We conclude that for each agent i, we have $P_i(1)=([\frac{\omega }{2},1-\omega ],[\omega ,1-\frac{\omega }{2}])$.

Consider an agent i in the next round. Then the choice $c_i=\frac{\omega }{2}$ is optimal for the belief $b_i$ with $b_i(1-\frac{\omega }{2},\ldots ,1-\frac{\omega }{2})$. Similarly, the choice $1-\frac{\omega }{2}$ is the optimal choice for agent i for the belief $b_i$ with $b_i(\frac{\omega }{2},\ldots ,\frac{\omega }{2})=1$. Similar to the case where $\frac{1}{3} < \omega \le \frac{1}{2}$, we can show that $c_i \in \{(\frac{\omega }{2},1-\omega ],[\omega ,1-\frac{\omega }{2})\}$ is not optimal for any point belief in $P_{-i}(1)$. As a result, the set of point rationalizable choices of each agent i is $P_i=\{\frac{\omega }{2},1-\frac{\omega }{2}\}$.

Lastly, consider $\frac{2}{3} < \omega \le 1$. Then again, the choice $c_i=\frac{\omega }{2}$ is optimal for the belief $b_i$ with $b_i(1-\frac{\omega }{2},\ldots ,1-\frac{\omega }{2})$. Similarly, the choice $1-\frac{\omega }{2}$ is the optimal choice for agent i for the belief $b_i$ with $b_i(\frac{\omega }{2},\ldots ,\frac{\omega }{2})=1$. In similar fashion as the $\frac{1}{3} < \omega \le \frac{1}{2}$ case, it can be shown that $c_i \in (\frac{\omega }{2},1-\frac{\omega }{2})$ is not optimal for any point belief. As a result, the set of point rationalizable choices of each agent i is $P_i= \{\frac{\omega }{2},1-\frac{\omega }{2}\}$. $\square$