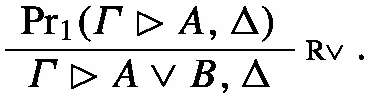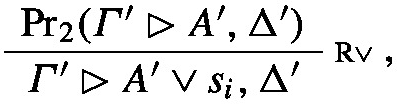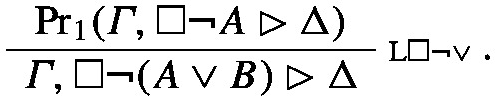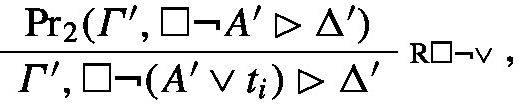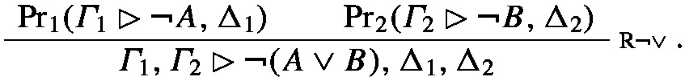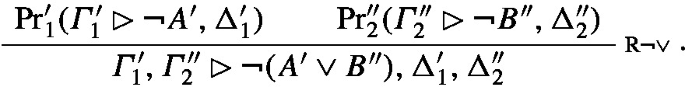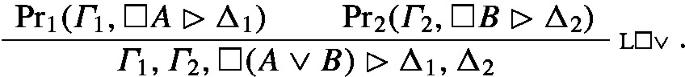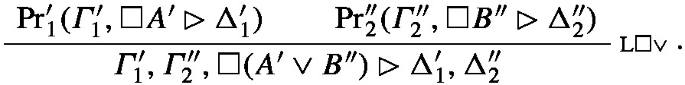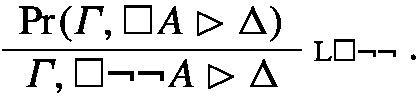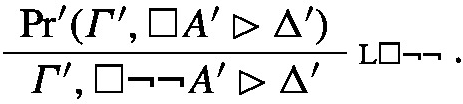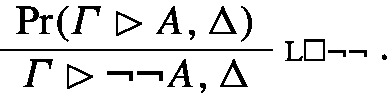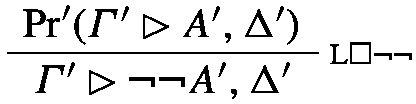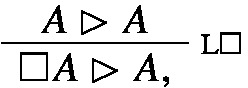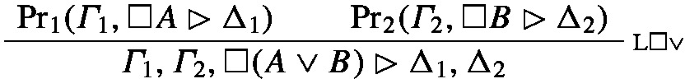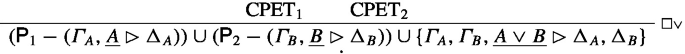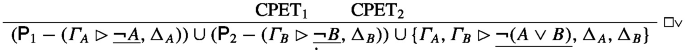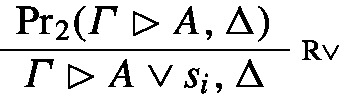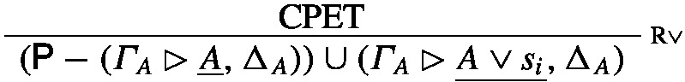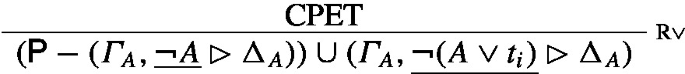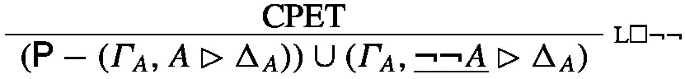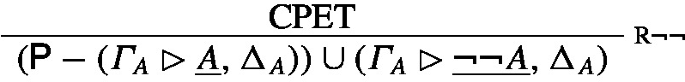Truthmakers and Relevance for FDE, LP, K3, and CL

Abstract

In this paper, we first develop truthmaker semantics for four relevance logics defined as the non-transitive relevant cores [as introduced in Verdée et al. (Aust J Log 16:10–40, 2019)] of the well-known propositional logics ${\textbf {CL}}$ (classical logic), ${\textbf {LP}}$ (the logic of paradox), ${\textbf {K3}}$ (strong Kleene logic), and ${\textbf {FDE}}$ (first degree entailment). The semantics is similar to Kit Fine’s truthmaker semantics for classical logic, but we define the notion of exact verification similarly to Fine’s notion of loose verification. Dropping Fine’s principle of Downward Closure of the set of consistent states nevertheless warrants the exactness of our verification notion. The semantics of the four non-transitive relevance logics shows that they are in fact straightforward cut-free substructural logics, despite their definition by means of a filtering criterion. We develop the associated sound and complete sequent calculi for these logics. Finally, we argue that the four presented truthmaker semantics are also interesting alternatives to the standard Kit Fine style truthmaker semantics for the original (irrelevant) consequence relations ${\textbf {FDE}}$, ${\textbf {LP}}$, ${\textbf {K3}}$, and ${\textbf {CL}}$ themselves. The most interesting difference with Fine’s approach is the way in which tautologies are handled: next to their usual verifiers, they are also made true by the empty state. We provide philosophical arguments for the plausibility of such an account.

Appendix: Metatheory

We need to prove that the present sequent calculus for the basic ${\textbf{L}^{\textbf{r}}}$-logics is sound and complete with respect to two relations: the X-relevant core filter relation $\vdash _{\textbf{L}^{\textbf{r}}}$ (Theorem 2) and the semantic consequence relation $\vDash _{\textbf{L}^{\textbf{r}}}$ (Theorem 1). To this end we will present each time a soundness proof and a completeness proof. The proof of the first theorem is entirely based on the proof presented in Verdée et al. (2019), but needed to be slightly adapted to account for the generalization to ${\textbf {LPR}}$, ${\textbf {K3R}}$, ${\textbf {FDER}}$.

Before starting the actual proofs, let us introduce the notion of an abstraction $\varGamma ^{\prime }\rhd \Delta ^{\prime }$ of a sequent $\varGamma \rhd \Delta$. The former sequent is an abstraction of the latter iff the latter is in the contraction closure of the US-closure of the former. In other words $\varGamma \rhd \Delta$ is the result of applying an arbitrary number of times Uniform Substitution, followed by an arbitrary number of times contraction to $\varGamma ^{\prime }\rhd \Delta ^{\prime }$. We will write $\varGamma ^{\prime }, A_1,\ldots , A_n\rhd \Delta ^{\prime }$ as an abstraction of $\varGamma , A\rhd \Delta$, if $A_1,\ldots , A_2$ are the formulas that are transformed into A by the Uniform Substitution and Contraction process. We say that $\varGamma \rhd \Delta$ is the flattening of $\varGamma ^\Box \rhd \Delta$ (flattening a sequent thus means removing the boxes in front of formulas on the left side). A sequent is a flattened non- ${\textbf {L}}$-redundant abstraction of another sequent iff the former is the flattening of an abstraction of the latter, the former is ${\textbf {L}}$-valid, and none of its proper subsequents are ${\textbf {L}}$-valid.

We first prove the adequacy of the sequent calculus w.r.t. ${\textbf{L}^{\textbf{r}}}$, i.e. the X-relevant core of ${\textbf {L}}$.

Theorem 2

For each basic consequence relation ${\textbf {L}}$, $\varGamma ^\Box \rhd \Delta$ is provable in an ${\textbf{L}^{\textbf{r}}}$-proof iff $\varGamma \vdash _{\textbf{L}^{\textbf{r}}}\Delta$.

Then we will prove the adequacy of the sequent calculus w.r.t. the semantical consequence relation of $\textbf{L}^{\textbf{e}}$.

Theorem 1

For each basic consequence relation ${\textbf {L}}$, $\varGamma \vDash _{\textbf{L}^{\textbf{e}}} \Delta$ iff there is an $\textbf{L}^{\textbf{e}}$-proof for $\varGamma \rhd \Delta$.

13.1.1 Soundness w.r.t. X-Relevant Core

The idea behind the soundness proof is that every ${\textbf{L}^{\textbf{r}}}$-proof can be abstracted in such a way that none of the sequents in the proof are ${\textbf {L}}$-redundant. We will define a procedure that transforms proofs in their abstractions and will show that the sequents in the abstracted proofs have a certain graph-theoretic property (in fact it is a generalized variable sharing-property). Finally we will show that sequents with that property are always non-redundant.

We start with some preparatory definitions. Let a literal be a sentential letter or its negation. For the abstractions we need to distinguish two mutually exclusive kinds of literals: those that matter for the sequent’s validity (i.e. they constitute a connection between two formulas of the sequent) and those that are replaceable by any other literal. $\mathscr {T}$ denotes the set of all these literals, $\mathscr {T}_c$ are the connecting literals and $\mathscr {T}_r$ are the replaceable ones. The four categories (the positive and negated ones in $\mathscr {T}_c$ and the positive and negative ones in $\mathscr {T}_r$) should not share any sentential letter. The set $\mathscr {T}_r$ will comprise all the $s_i$ and $\lnot t_i$, where $i\in \mathbb {N}$. A typical ${\textbf {L}}$-model is one in which, for all $\rho \in \mathscr {S}$, $v_T(\rho )=no(v_F(\rho ))$, all $|s_i|=\emptyset$ and all $|t_i|=\mathscr {S}$ (all set of states). We will say that a formula A is true resp. untrue in a state s of an ${\textbf {L}}$-model M iff $s\in |A|_M$ resp. $s\not \in |A|_M$ and that A is false resp. unfalse in a state s of an ${\textbf {L}}$-model M iff $s\in |\lnot A|_M$ resp. $s\not \in |\lnot A|_M$. This means that $s_i$ is always untrue and $t_i$ always true in all states of typical ${\textbf {L}}$-models. In typical ${\textbf {L}}$-models, by the way, untrue is identical to false and unfalse is identical to true, because of the restriction that $v_T(\rho )=no(v_F(\rho ))$, i.e. typical ${\textbf {L}}$-models are always classical.

The proof goes as follows. Suppose there is an ${\textbf{L}^{\textbf{r}}}$-proof for $\varGamma ^\Box \rhd \Delta$. We will first devise a procedure that transforms any ${\textbf{L}^{\textbf{r}}}$-proof into what we we call its canonical abstraction. We will then show that the conclusion sequent of the canonically abstracted proof is what we will call a typical ${\textbf {L}}$-abstraction of $\varGamma ^\Box \rhd \Delta$. We get to the soundness result by showing, for every $\varGamma$, $\Delta$, that, if $\varGamma ^\Box \rhd \Delta$ has a typical ${\textbf {L}}$-abstraction, then also $\varGamma \rhd \Delta$ is ${\textbf{L}^{\textbf{r}}}$-valid.

We first give the procedure for the transformation of an ${\textbf{L}^{\textbf{r}}}$-proof into its canonical abstraction.

Definition 25

The canonical abstraction of ${\textbf{L}^{\textbf{r}}}$-proof is recursively defined as follows.

Basic case. The proof is of the form

where B is not of the form $\lnot A$. Its canonical abstraction is then

Recursion step.

• The proof is of the form

  

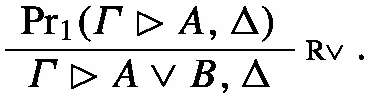
  Let $\textrm{Pr}_2(\varGamma ^{\prime }\rhd A^{\prime },\Delta ^{\prime })$ be the canonical abstraction of $\textrm{Pr}_1(\varGamma \rhd A,\Delta )$. The canonical abstraction of the entire proof is then

  

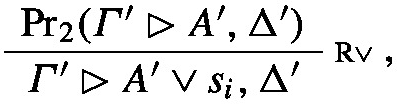
  where i is a natural number such that $s_i$ does not yet occur in $\varGamma ,\Delta , A$

• The proof is of the form

  

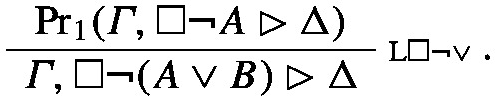
  Let $\textrm{Pr}_2(\varGamma ^{\prime },\Box \lnot A^{\prime }\rhd \Delta ^{\prime })$ be the canonical abstraction of $\textrm{Pr}_1(\varGamma , \Box \lnot A\rhd \Delta )$. The canonical abstraction of the entire proof is then

  

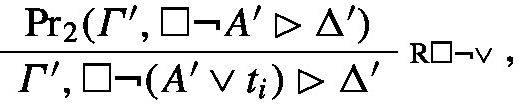
  where i is a natural number such that $t_i$ does not yet occur in $\varGamma ,\Delta , A$

• The proof is of the form

  

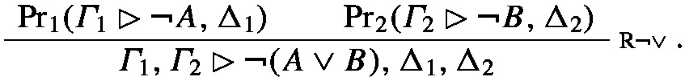
  Let $\textrm{Pr}^{\prime }_1(\varGamma _1^{\prime }\rhd \lnot A^{\prime },\Delta _1^{\prime })$ be the canonical abstraction of $\textrm{Pr}_1(\varGamma _1\rhd \lnot A,\Delta _1)$ and let $\textrm{Pr}^{\prime }_2(\varGamma _2^{\prime }\rhd \lnot B^{\prime },\Delta ^{\prime }_2)$ be the canonical abstraction of $\textrm{Pr}_2(\varGamma _2\rhd \lnot B,\Delta _2)$. Let $\textrm{Pr}^{\prime \prime }_2(\varGamma _2^{\prime }\rhd \lnot B^{\prime \prime },\Delta ^{\prime \prime }_2)$ be a relettering of the latter canonical abstraction such that it has no letters in common with $\varGamma _1^{\prime }$, $\Delta _1^{\prime }$ or $A^{\prime }$. The canonical abstraction of the entire proof is then

  

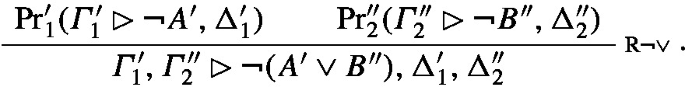
• The proof is of the form

  

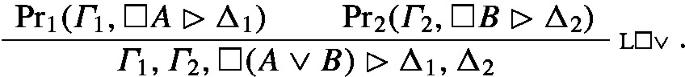
  Let $\textrm{Pr}^{\prime }_1(\varGamma _1^{\prime },\Box A^{\prime }\rhd \Delta _1^{\prime })$ be the canonical abstraction of $\textrm{Pr}_1(\varGamma _1,\Box A\rhd \Delta _1)$ and let $\textrm{Pr}^{\prime }_2(\varGamma _2^{\prime },\Box B^{\prime }\rhd \Delta ^{\prime }_2)$ be the canonical abstraction of $\textrm{Pr}_2(\varGamma _2,\Box B\rhd \Delta _2)$. Let $\textrm{Pr}^{\prime \prime }_2(\varGamma ^{\prime }_2,\Box B^{\prime \prime }\rhd \Delta ^{\prime \prime }_2)$ be a relettering of the latter canonical abstraction such that it has no letters in common with $\varGamma _1^{\prime }$, $\Delta _1^{\prime }$ or $A^{\prime }$. The canonical abstraction of the entire proof is then

  

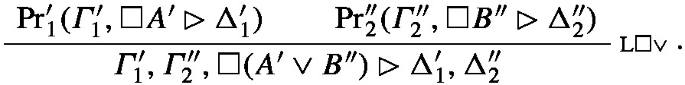
• The proof is of the form

  

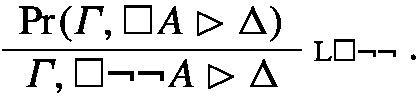
  The canonical abstraction is

  

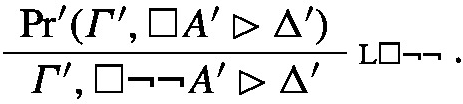
  where $\textrm{Pr}^{\prime }(\varGamma ^{\prime },\Box A^{\prime }\rhd \Delta ^{\prime })$ is the canonical abstraction of $\textrm{Pr}(\varGamma ,\Box A\rhd \Delta )$.

• The proof is of the form

  

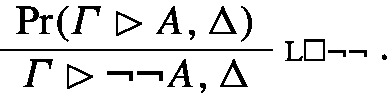
  The canonical abstraction is

  

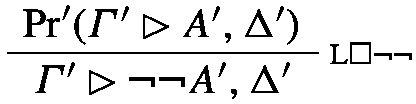
  where $\textrm{Pr}^{\prime }(\varGamma ^{\prime }\rhd A, \Delta ^{\prime })$ is the canonical abstraction of $\textrm{Pr}(\varGamma \rhd A, \Delta )$.

• Contraction rules. It suffices to just remove that rule from the proof and keep multiple copies of specific formulas.

Let us illustrate this with an example. Consider the ${\textbf {CLR}}$-valid and ${\textbf {LPR}}$-valid example sequent

$$ (q\vee \lnot r)\wedge (q\vee r) \rhd r, q\wedge q\wedge \lnot r, \lnot r\vee (p\wedge q) , \lnot r\vee q. $$

A proof for that sequent can be found in Fig. 13.2 and the canonical abstraction of that proof in Fig. 13.3. The original sequent is thus abstracted into

$$ \Box ((p\vee \lnot p_1) \wedge t_1), \Box ((q\vee \lnot p_2)\wedge t_2)\rhd r, p\wedge q\wedge \lnot r, \lnot p_1\vee s_2 , \lnot p_2\vee s_3. $$

Fig. 13.2

A ${\textbf {CLR}}$-proof for $(q\vee \lnot r)\wedge (q\vee r) \rhd r, q\wedge q\wedge \lnot r, \lnot r\vee (p\wedge q) , \lnot r\vee q$

Fig. 13.3

The canonical abstraction of the proof in Fig. 13.2

We build up the characterization of typical abstractions step by step.

Definition 26

A positive resp. negative ${\textbf {L}}$-prime sequent for a formula A resp. B is a sequent of the form $\varGamma \rhd \underline{A}, \Delta$ resp. $\varGamma , \underline{B}\rhd \Delta$, where $\varGamma \cup \Delta \subseteq \mathscr {T}_c$, such that,

• (i) the sequent is ${\textbf {L}}$-valid,

• (ii) for all $C\in \varGamma$ and for all states s in all typical $\textbf{L}$-models M, if C is false in s, then B is true and A is false in s

• (iii) for all $D\in \Delta$ and for all states s in all typical $\textbf{L}$-models M, if D is true in s, then B is true in s and A is false in s.¹⁴

As an example, consider the formula $(p\vee \lnot q)\wedge (\lnot r\vee s)$. $(p\vee s_1)\wedge (\lnot r\vee s_2)$ and $(p\vee \lnot q)\wedge t_1$ are abstractions of this formula.

$$ p, \lnot r\rhd \underline{(p\vee s_1)\wedge (\lnot r\vee s_2)} $$

is a positive ${\textbf {FDE}}$-prime sequent of the first abstraction and

$$ \underline{(p\vee \lnot q)\wedge t_i}\rhd p,\lnot q $$

is a negative ${\textbf {FDE}}$-prime sequent of the second abstraction.

$$ p\rhd \underline{(p\vee s_1)\wedge (\lnot r\vee s_2)}, r $$

and

$$ q,\underline{(p\vee \lnot q)\wedge t_1}\rhd p $$

are positive resp. negative ${\textbf {CL}}$-prime sequents of the same abstractions, the first also being ${\textbf {LP}}$-prime (but not ${\textbf {K3}}$-prime), the second also being ${\textbf {K3}}$-prime (but not ${\textbf {LP}}$-prime).

If $\varGamma \rhd \underline{A}, \Delta$ resp. $\varGamma , \underline{B}\rhd \Delta$ are the ${\textbf {L}}$-prime sequents for A resp. B, $\varGamma$ are called the positive literals of A resp. B, while $\Delta$ are the negative literals of A resp. B. To every set of ${\textbf {L}}$-prime sequents $\textsf{P}$ corresponds a characteristic graph. This undirected graph is defined as follows: the vertices of the graph are the members of $\textsf{P}$ and the edges are the connecting literals C that connect two vertices $\varGamma _1\rhd \underline{C},\Delta _1$ and $\varGamma _2,\underline{C}\rhd \Delta _2$.

Definition 27

A set of ${\textbf {L}}$-prime sequents is an ${\textbf {L}}$-prime expansion of a sequent $\varGamma \rhd \Delta$ iff it contains exactly one positive resp. negative ${\textbf {L}}$-prime sequent for each member of $\Delta$ resp. $\varGamma$, and nothing else.

It is instructive to consider ${\textbf {CL}}$-prime expansion of the abstraction of the example sequent we constructed earlier on in the proof. We draw its characteristic graph in Fig. 13.4.

$$\begin{aligned} \underline{(p\vee \lnot p_1)\wedge t_1} & \rhd p, \lnot p_1 \end{aligned}$$

(13.1)

$$\begin{aligned} \underline{(q\vee \lnot p_2)\wedge t_2} & \rhd q,\lnot p_2 \end{aligned}$$

(13.2)

$$\begin{aligned} r & \rhd \underline{r} \end{aligned}$$

(13.3)

$$\begin{aligned} p, q & \rhd \underline{(p\wedge q\wedge \lnot r)\vee s_1}, r \end{aligned}$$

(13.4)

$$\begin{aligned} \lnot p_1 & \rhd \underline{\lnot p_1\vee s_2}\end{aligned}$$

(13.5)

$$\begin{aligned} \lnot p_2 & \rhd \underline{\lnot p_2\vee s_3} \end{aligned}$$

(13.6)

Fig. 13.4

The graph defined by our example’s prime expansion

These sequents are all ${\textbf {CL}}$-valid and ${\textbf {LP}}$-valid. One can verify that, if all $t_i$ are true and all $s_i$ are untrue, the underlined formulas on the left are true and those on the right are untrue whenever one of the literals on right are true and whenever one of the literals on the left is untrue. This suffices to show that the sequents are indeed ${\textbf {L}}$-prime sequents of the underlined formulas. We moreover have exactly one ${\textbf {L}}$-prime sequent for each formula in the example sequent.

For every canonical abstraction $Pr(\varGamma ^\Box \rhd \Delta )$ of an ${\textbf{L}^{\textbf{r}}}$ proof, we devise a procedure that transforms every sequent in $Pr(\varGamma ^\Box \rhd \Delta )$ into a prime expansion of its flattening. We call the resulting tree (replacing every sequent in the proof by a prime expansion of its flattening) the canonical prime expansion of the proof.

• The proof is of the form

  

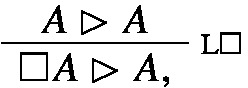
  where $A\in \mathscr {L}\mathscr {I}\mathscr {T}$. The canonical prime expansion tree of the proof is the single node tree $\{\underline{A}\rhd A, A\rhd \underline{A}\}$.

• The final rule of the proof is L$\Box \vee$.

  

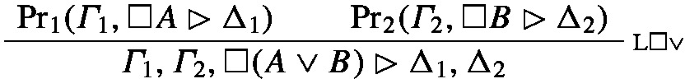
  Let $\textrm{CPET}_1$ be the canonical prime expansion tree of the proof $\textrm{Pr}_1(\varGamma _1, \Box A\rhd \Delta _1)$ and let let $\textrm{CPET}_2$ be the canonical prime expansion tree of the proof $\textrm{Pr}_2(\varGamma _2, \Box B\rhd \Delta _2)$. If $\textsf{P}_1$ resp. $\textsf{P}_2$ are the prime expansions of the conclusion sequent of $\textrm{CPET}_1$ resp. $\textrm{CPET}_2$, the canonical prime expansion tree is

  

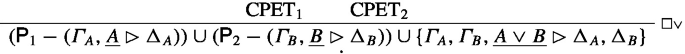
• The final rule of the proof is R$\lnot \vee$. Similarly to the previous case the canonical prime expansion tree will be

  

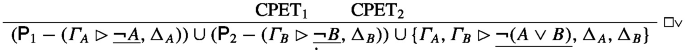
• The final rule of the proof is R$\vee$. The proof is of the form

  

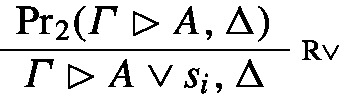
  Let $\textrm{CPET}$ be the canonical prime expansion tree of the proof $\textrm{Pr}_2(\varGamma \rhd A,\Delta )$. If $\textsf{P}$ is the prime expansion of $\varGamma \rhd A,\Delta$, which is obtained as the root of $\textrm{CPET}$, the canonical prime expansion of the total proof is

  

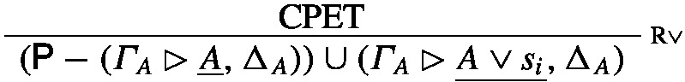
  where $\varGamma _{A}\rhd \underline{A},\Delta _{A}$ is the positive prime sequent for A in $\textsf{P}$.

• The final rule of the proof is L$\Box \lnot \vee$. Similarly to the previous case the canonical prime expansion tree will be

  

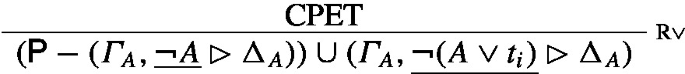
  where $\varGamma _{A}, \underline{\lnot A}\rhd \Delta _{\lnot A}$ is the negative prime sequent for $\lnot A$ in $\textsf{P}$.

• The final rule of the proof is L$\Box \lnot \lnot$. Similarly to the previous case the canonical prime expansion tree will be

  

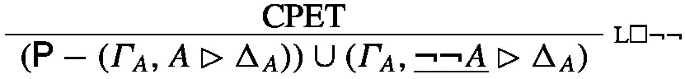
  where $\varGamma _{A}, \underline{A}\rhd \Delta _{A}$ is the negative prime sequent for A in $\textsf{P}$.

• The final rule of the proof is R$\lnot \lnot$. Similarly to the previous case the canonical prime expansion tree will be

  

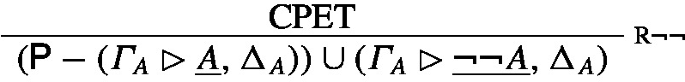
  where $\varGamma _{A}\rhd \underline{A}, \Delta _{A}$ is the positive prime sequent for A in $\textsf{P}$.

Definition 28

A typical ${\textbf {L}}$-abstraction of a sequent $\varGamma ^{\prime }\rhd \Delta ^{\prime }$ is an abstraction $\varGamma \rhd \Delta$ of $\varGamma ^{\prime }\rhd \Delta ^{\prime }$ that has an ${\textbf {L}}$-prime expansion $\textsf{P}$, the characteristic graph of which is a tree (i.e. it is acyclic).

Lemma 1

Every sequent that has a typical ${\textbf {L}}$-abstraction is ${\textbf{L}^{\textbf{r}}}$-valid.

Proof

Suppose $\varGamma \rhd \Delta$ is a typical ${\textbf {L}}$-abstraction of $\varGamma ^{\prime }\rhd \Delta ^{\prime }$. We will show that then $\varGamma ^{\prime }\vdash _{\textbf{L}^{\textbf{r}}}\Delta ^{\prime }$. It suffices to prove that $\varGamma \rhd \Delta$ is non-${\textbf {L}}$-redundant. In order to establish that we need to show that $\varGamma \vdash _{\textbf{L}}\Delta$, $\varGamma -\{A\}\nvdash _{\textbf{L}}\Delta$ and $\varGamma \nvdash _{\textbf{L}}\Delta -\{B\}$ for every $A\in \varGamma$ and $B\in \Delta$.

By Definition 28, we know that $\varGamma \rhd \Delta$ has a prime expansion $\textsf{P}$ with a characteristic graph $\langle \textsf{P}, E\rangle$, where the set of edges E is the set of literals that connect two sequents, by occurring as a conclusion in the first sequent and as a premise in the second. All vertices are ${\textbf {L}}$-valid sequents by the definition of a prime expansion.

Every edge in the characteristic graph corresponds to a literal A, connecting a sequent $\varGamma _1, A\rhd \Delta _1$ and $\varGamma _2\rhd A, \Delta _2$. We can construct a new acyclic graph of ${\textbf {L}}$-valid sequents by removing the two vertices and replacing them by the single vertex $\varGamma _1,\varGamma _2\rhd \Delta _1,\Delta _2$, connected by an edge with all the other neighbours of the original vertices. We can keep fusing vertices until just one vertex is left. This will be the vertex $\varGamma \rhd \Delta$, which is ${\textbf {L}}$-valid because all the vertices of all the graphs in the graph transformation process are.

Next we need to prove that removing one of the formulas in the sequent $\varGamma \rhd \Delta$ results in an ${\textbf {L}}$-invalid sequent. Let $\varGamma ^{\prime \prime }\rhd \Delta ^{\prime \prime }$ be a sequent that contains exactly one formula (premise or conclusion) less than $\varGamma \vdash \Delta$. We prove this by constructing an ${\textbf {L}}$-typical model that falsifies one premise literal or verifies exactly one conclusion literal in every sequent in the prime expansion of $\varGamma ^{\prime \prime }\rhd \Delta ^{\prime \prime }$. By the definition of a prime sequent and the fact that all ${\textbf {L}}$-typical models are classical,¹⁵ this makes every main formula of every prime sequent in the prime expansion true if it is a premise and untrue if it is a conclusion. This will prove that $\varGamma ^{\prime \prime }\nvdash _{\textbf{L}}\Delta ^{\prime \prime }$. We construct the ${\textbf {L}}$-typical model by associating either the label ‘true’ or the label ‘false’ to each edge of the acyclic graph. All premise resp. conclusion literals in the prime sequent of the removed sequent get the label ‘true’ reps. ‘false’. The rest of the graph is associated with labels in such a way that no two adjacent edges get the same label (basic graph theory shows that this is always possible).

We can show that this construction amounts to verifying one conclusion literal or falsifying one premise literal in each sequent in $\textsf{P}$, except for the prime sequent of the removed formula. This property holds for the adjacent vertices of the removed formula’s sequent, because all the premise literals of the removed formula’s sequent are verified and each adjacent vertex contains as a premise a conclusion literal of the removed formula’s sequent and as a conclusion a premise literal of the latter sequent. If, in a sequent a literal has been labelled, the other literals by the labelling procedure become verified if they are premises and falsified if they are conclusions. The adjacent vertices will then also have a literal whose labelling falsifies its main formula, exactly like in the case of the adjacent vertices of the removed formula’s sequent. And so on.

We still need to show that one ${\textbf {L}}$-model can indeed verify/falsify all these premise and conclusion literals. This is the case, because negated and positive literals do not share letters and if a same literal should be both a premise and a conclusion literal, there would need to be an extra edge between the vertices that contain them. This is impossible because the graph is acyclic.

Lemma 2

Let $\textrm{Pr}(\varGamma ^\Box \rhd \Delta )$ be an ${\textbf{L}^{\textbf{r}}}$-proof. The characteristic graph corresponding to every prime expansion in the canonical prime expansion tree of the canonical abstraction of $\textrm{Pr}(\varGamma ^\Box \rhd \Delta )$ is acyclic.

Proof

The proof is rather straightforward. There are three kinds of graph transformations that correspond to the rules in the corresponding canonical prime expansion tree.

• Basic case: single root canonical prime expansion trees. The characteristic graph of the only prime expansion in this tree consists of two vertices that are connected by one edge. Such graph is evidently acyclic.

• Induction case 1. Canonical prime expansion trees the root of which correspond to the rules $L\Box \vee$ and $R\lnot \vee$. We transform two graphs $G_1$ and $G_2$ that have no literals in common into a graph that combines both graphs by fusing one vertex of each graph into a vertex that is connected to all the neighbours of the fused vertices. Given that there is only one edge in the resulting graph connecting the two subgraphs, the resulting graph is acyclic if the original graphs are.

• Induction case 2. Canonical prime expansion trees the root of which correspond to one of the other rules. No new edges or vertices are created by means of this transformation, no edges or vertices are removed. One vertex is transformed in another one without changing the edges it has that connect it to the other vertices. The graph stays structurally identical and so is acyclic if the original one is.

Theorem 3

If there is an ${\textbf{L}^{\textbf{r}}}$-proof for $\varGamma ^\Box \rhd \Delta$, then $\varGamma \vdash _{\textbf{L}^{\textbf{r}}} \Delta$.

Proof

Suppose there is an ${\textbf{L}^{\textbf{r}}}$-proof $\textrm{Pr}(\varGamma ^\Box \rhd \Delta )$ for $\varGamma ^\Box \rhd \Delta$. By Lemma 2, we know that there is the characteristic graph corresponding to every prime expansion in the canonical prime expansion tree of the canonical abstraction $\textrm{Pr}(\varGamma ^{\prime \Box }\rhd \Delta ^{\prime })$ of $\textrm{Pr}(\varGamma ^\Box \rhd \Delta$ is acyclic. By Definition 28, $\varGamma ^{\prime }\rhd \Delta ^{\prime }$ is a typical ${\textbf {L}}$-abstraction of $\varGamma \rhd \Delta$ and, by Lemma 1, $\varGamma ^{\prime }\rhd \Delta ^{\prime }$ is ${\textbf{L}^{\textbf{r}}}$-valid. Because $\varGamma ^{\prime }\rhd \Delta ^{\prime }$ is an abstraction of $\varGamma \rhd \Delta ^{\prime }$ and ${\textbf{L}^{\textbf{r}}}$ is closed under Contraction and Uniform Substitution, the latter is then also ${\textbf{L}^{\textbf{r}}}$-valid.

13.1.2 Completeness w.r.t. the X-Relevant Core

A proto-${\textbf{L}^{\textbf{r}}}$-proof is exactly like an ${\textbf{L}^{\textbf{r}}}$-proof, except for the axiom rule being the more general

$$ \varGamma , A\rhd A,\Delta . $$

Note that this removes the relevance characteristic of the proofs, as irrelevant literals are allowed.

A tableau-like ${\textbf{L}^{\textbf{r}}}$-tree is a proto-${\textbf{L}^{\textbf{r}}}$-proof in which for disjunctions and negations of conjunctions (i.e. negation of disjunction) only the following four derived rules are allowed.

Lemma 3

For every $\varGamma$ and $\Delta$ there is a tableau-like ${\textbf{L}^{\textbf{r}}}$-tree the leaves of which are sequents consisting only of literals.

Lemma 4

If $\varGamma \vdash _{\textbf{L}} \Delta$ then there is a tableau-like proto-${\textbf{L}^{\textbf{r}}}$-proof for $\varGamma ^\Box \rhd \Delta$.

For the proof of the next lemma, one simply needs to check each rule case by case

Lemma 5

It is possible to prune proto-${\textbf{L}^{\textbf{r}}}$-proofs from the leaves to the root. If there is a proto-${\textbf{L}^{\textbf{r}}}$-proof of the form

and there also is a proto-${\textbf{L}^{\textbf{r}}}$-proof $\textrm{Pr}_1(\varGamma _1^{\prime }\rhd \Delta _1^{\prime })$ resp. $\textrm{Pr}_2(\varGamma _2^{\prime }\rhd \Delta _2^{\prime })$ for some proper subsequent of $\varGamma _1\rhd \Delta _1$ resp. $\varGamma _2\rhd \Delta _2$, then there is a proof of a (proper or improper) subsequent of $\varGamma _3 \rhd \Delta _3$, only using the subproofs $\textrm{Pr}_1(\varGamma _1^{\prime }\rhd \Delta _1^{\prime })$ and/or $\textrm{Pr}_2(\varGamma _2^{\prime }\rhd \Delta _2^{\prime })$.

Theorem 4

If $\varGamma \vdash _{\textbf{L}^{\textbf{r}}} \Delta$, then there is an ${\textbf{L}^{\textbf{r}}}$-proof for $\varGamma ^\Box \rhd \Delta$.

Proof

Suppose $\varGamma \vdash _{\textbf{L}^{\textbf{r}}} \Delta$.

Then there is a non-${\textbf{L}^{\textbf{r}}}$-redundant abstraction $\varGamma _a\rhd \Delta _a$ of $\varGamma \rhd \Delta$. Because $\varGamma _a\vdash _{\textbf{L}} \Delta _a$, Lemma 4 warrants that there be a tableau-like proto-${\textbf{L}^{\textbf{r}}}$-proof for $\varGamma _a^\Box \rhd \Delta _a$. Consider this proto-proof. The leaves of this proto-proof tree are of the form $\varGamma ^{\prime }, A\rhd A,\Delta ^{\prime }$, where A and the members of $\varGamma ^{\prime }$ and $\Delta ^{\prime }$ are all literals. For each leave remove now the ‘redundant’ literals, i.e. the members of $\varGamma ^{\prime }$ and $\Delta ^{\prime }$. Lemma 5 indicates that we can adjust the tree top-down by removing redundant formulas in all subsequent sequents closer to the root. The result of this pruning process is an ${\textbf{L}^{\textbf{r}}}$-proof (the leaves now all correspond to ${\textbf{L}^{\textbf{r}}}$-axioms) with as its root sequent (the final conclusion) a proper or improper subsequent of $\varGamma _a^\Box \rhd \Delta _a$. But if it were a proper subsequent, we would have constructed an ${\textbf {L}}$-proof (note that ${\textbf{L}^{\textbf{r}}}$-proof are sound w.r.t. ${\textbf {L}}$) for a proper subsequent of $\varGamma _a^\Box \rhd \Delta _a$ and so there would be an ${\textbf {L}}$-valid subsequent of $\varGamma _a\rhd \Delta _a$. This is impossible in view of the sequent being non-${\textbf{L}^{\textbf{r}}}$-redundant.

So the final conclusion of the constructed ${\textbf {L}}$-proof is exactly $\varGamma _a^\Box \rhd \Delta _a$. We can now instantiate this proof (and add LCON and RCON application where necessary) to obtain an ${\textbf{L}^{\textbf{r}}}$-proof of $\varGamma ^\Box \rhd \Delta$.

Let us give an example of this pruning process. We start with a tableau-like proto-${\textbf {CLR}}$-proof for $\Box p, \Box (\lnot p\vee r)\rhd r\vee s$.

We now eliminate the derived rules L$\Box \vee$f and R$\vee$f.

First pruning removes the redundant r in the first leaf.

Second pruning removes the redundant s in the first leaf.

Third pruning removes the redundant s in the second leaf.

Fourth pruning removes the redundant $\Box p$ in the second leaf.

The latter is finally a correct ${\textbf{L}^{\textbf{r}}}$-proof.

13.1.3 Adequacy w.r.t Semantic $\textbf{L}^{\textbf{e}}$-Consequence

From now on, we will use the notation $\varGamma \vdash _{\textbf{L}^{\textbf{e}}} \Delta$ to refer to the fact that the sequent $\varGamma \rhd \Delta$ can be proven by means of the sequent calculus for $\textbf{L}^{\textbf{e}}$.

We remind the reader that the truthmaker semantics of $\textbf{L}^{\textbf{e}}$ is a Closure Semantics as introduced in Chap. 12 of Restall (2000). More specifically it is a variant of the phase space semantics, which is a semantics originally developed for Linear Logic. The adequacy proofs of $\vdash _{\textbf{L}^{\textbf{e}}}$ w.r.t. $\vDash _{\textbf{L}^{\textbf{e}}}$ are based on the general soundness and completeness proofs for Closure Semantics presented in Sect. 12.3 of the book.¹⁶ Soundness does not pose specific difficulties here and we safely leave the proof to the reader.

So let us start the completeness proof. We need some preliminary notions. Without loss of generality,¹⁷ we slightly enrich the language to later simplify the construction of a canonical model. Let $\mathscr {W}^+=_{df}\mathscr {W}_\Box \cup \{A \& B\mid A, B\in \mathscr {W}_\Box \} \cup \bot$, i.e. the language $\mathscr {W}_\Box$ to which the bottom particle $\bot$ and the extensional conjunction & is added at the outer level. The semantic clause for $\bot$ is

$$ |\bot |=S-S^\Diamond , $$

its only sequent calculus rule is

The semantic clause for & is

$$ |A \& B|=|A|\cap |B| $$

and the sequent calculus rules are

Let $\mathscr {U}=_{df}$ the set of multisets of members of $\mathscr {W}^+$ in which each member occurs only once. $\Sigma$ and $\varTheta$, possibly with subscripts, superscripts, and/or accentuation, will be variables for members of $\mathscr {U}$.

Proving the following fact is far from evident as it amounts to proving Gentzen’s Cut Elimination for the sequent calculi enriched with the Cut-rule in this paper. However, its proof can quite straightforwardly be obtained from the generalized cut elimination proof in Chap. 6 of Restall (2000).

Fact 8

$\vdash _{\textbf{L}^{\textbf{e}}}$ is transitive (if $\varGamma _1\vdash _{\textbf{L}^{\textbf{e}}} A, \Delta _1$ and $\varGamma _2, A\vdash _{\textbf{L}^{\textbf{e}}} \Delta _2$, then $\varGamma _1,\varGamma _2\vdash _{\textbf{L}^{\textbf{e}}} \Delta _1,\Delta _2$).

The completeness proof itself is realized by means of constructing for each of the four $\vdash _{\textbf{L}^{\textbf{e}}}$ what we call its canonical ${\textbf{L}^{\textbf{r}}}$-model. After having proven that this is indeed an ${\textbf{L}^{\textbf{r}}}$-model according to our truthmaker semantics, we obtain completeness by showing that this model serves as a countermodel for any unprovable sequent of $\textbf{L}^{\textbf{e}}$’s sequent calculus. Let $\Sigma \cup _s \varTheta =_{df} (\Sigma \cup \varTheta )- (\Sigma \cap \varTheta )$, i.e. the union from which all duplicates are removed.

Definition 29

The canonical ${\textbf{L}^{\textbf{r}}}$-model¹⁸ is the quadruple $\langle S, S^\Diamond , \sqsubseteq , v_\cdot \rangle$, where

• $S = \{\Sigma \rhd \varTheta \mid \Sigma ,\varTheta \in \mathscr {U}\}$

• $S^\Diamond = \{\Sigma \rhd \varTheta \mid \Sigma \nvdash _{\textbf{L}^{\textbf{e}}} \varTheta \}$

• $\sqsubseteq$ is the partial order relation that corresponds to the join operation $\sqcup$ defined by: $\Sigma _1\rhd \varTheta _1\sqcup \Sigma _2\rhd \varTheta _2 =_{df} \Sigma _1\cup _s \Sigma _2\rhd \varTheta _1\cup _s \varTheta _2$, and

• $\Sigma \rhd \varTheta \in v_T(\rho )$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{\rho \}\cup _s\varTheta$

• $\Sigma \rhd \varTheta \in v_F(\rho )$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{\lnot \rho \}\cup _s\varTheta$

• $\Sigma \rhd \varTheta \in v_{ST}(\rho )$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{\Box \rho \}\cup _s\varTheta$

• $\Sigma \rhd \varTheta \in v_{SF}(\rho )$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{\Box \lnot \rho \}\cup _s\varTheta$

We need to prove that this is indeed an ${\textbf{L}^{\textbf{r}}}$-model. The following two facts about the canonical model follow directly from the definition of the $no(\cdot )$ and $\cdot ^l$ operators.

Fact 9

For any proposition T: $\Sigma \rhd \varTheta \in no(T)$ iff $\forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\rhd \varTheta ^{\prime }\in T \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }).$

Fact 10

For any proposition T: $\Sigma \rhd \varTheta \in T^l$ iff $\forall \Sigma ^{\prime },\varTheta ^{\prime } [\forall \Sigma ^{\prime \prime },\varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in T \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime }) \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }].$

Lemma 6

The canonical ${\textbf{L}^{\textbf{r}}}$-model is an ${\textbf{L}^{\textbf{r}}}$-model.

Proof

We need to prove that the canonical model satisfies all properties of an ${\textbf{L}^{\textbf{r}}}$-model.

• $\sqcup$ is associative, commutative, and idem-potent because $\cup _s$ is.

• $\sqcup$ has a neutral element: $\emptyset \rhd \emptyset$, because $\Sigma \rhd \varTheta \sqcup \emptyset \rhd \emptyset = \Sigma \rhd \varTheta$.

• For all $\rho \in \mathscr {S}$, $v_{ST}(\rho )\subseteq v_{T}(\rho )$. Because $\Box \rho \vdash _{\textbf{L}^{\textbf{e}}} \rho$ and the transitivity of $\vdash _{\textbf{L}^{\textbf{e}}}$, we obtain that $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \rho ,\varTheta$ if $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \Box \rho ,\varTheta$.

• For all $\rho \in \mathscr {S}$, $v_{SF}(\rho )\subseteq v_F(\rho )$. Because $\Box \lnot \rho \vdash _{\textbf{L}^{\textbf{e}}} \lnot \rho$ and the transitivity of $\vdash _{\textbf{L}^{\textbf{e}}}$, we obtain that $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \lnot \rho ,\varTheta$ if $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \Box \lnot \rho ,\varTheta$.

• Where ${\textbf {L}}$ is ${\textbf {LP}}$ or ${\textbf {CL}}$: $no(v_F(\rho ))\subseteq (v_{ST}(\rho ))^l$. Suppose $\Sigma \rhd \varTheta \in no(v_F(\rho ))$. Then, by Fact 9,

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\rhd \varTheta ^{\prime }\in v_F(\rho ) \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }) $$

  or equivalently

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\lnot \rho \}\cup _s \varTheta ^{\prime }\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }). $$

  Because of the rule $\lnot$R, this entails

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\cup _s \{\Box \rho \}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }). $$

  Take $\Sigma ^{\prime }=\emptyset$ and $\varTheta ^{\prime }=\{\Box \rho \}$. This gives us

  $$ \Box \rho \vdash _{\textbf{L}^{\textbf{e}}}\Box \rho \ \Rightarrow \Sigma \vdash _{\textbf{L}^{\textbf{e}}}\{\Box \rho \}\cup _s \varTheta , $$

  or, with $A\vdash _{\textbf{L}^{\textbf{e}}}A$ and Modus Ponens, we get $\Sigma \vdash _{\textbf{L}^{\textbf{e}}}\Box \rho , \varTheta$ and therefore also $\Sigma \rhd \varTheta \in v_{ST}(\rho )$, which entails that $\Sigma \rhd \varTheta \in (v_{ST}(\rho ))^l$.

• Where ${\textbf {L}}$ is ${\textbf {LP}}$ or ${\textbf {CL}}$: $no(v_T(\rho ))\subseteq (v_{SF}(\rho ))^l$. Suppose $\Sigma \rhd \varTheta \in no(v_T(\rho ))$. Then, by Fact 9,

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\rhd \varTheta ^{\prime }\in v_T(\rho ) \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }) $$

  or equivalently

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\rho \}\cup _s \varTheta ^{\prime }\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }). $$

  By $\lnot \lnot A\vdash _{\textbf{L}^{\textbf{e}}}A$ and Fact 8, we get

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\lnot \lnot \rho \}\cup _s \varTheta ^{\prime }\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }). $$

  The rest of the proof goes exactly as the previous item.

• Where ${\textbf {L}}$ is ${\textbf {K3}}$ or ${\textbf {CL}}$: $(v_{ST}(\rho ))^l\subseteq no(v_F(\rho ))$. Suppose $\Sigma \rhd \varTheta \in (v_{ST}(\rho ))^l$. Then

  $$\begin{aligned} \forall \Sigma ^{\prime },\varTheta ^{\prime } [\forall \Sigma ^{\prime \prime },\varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in v_{ST}(\rho ) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}& \varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })\\ \Rightarrow & \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }].\nonumber \end{aligned}$$

  Hence

  $$\begin{aligned}\forall \Sigma ^{\prime },\varTheta ^{\prime } [\forall \Sigma ^{\prime \prime },\varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\Box \rho \}\cup _s \varTheta ^{\prime \prime }\Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}&\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })\\ \Rightarrow & \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }].\nonumber \end{aligned}$$

  Consequently, by $\lnot$R, we get

  $$\begin{aligned} \forall \Sigma ^{\prime },\varTheta ^{\prime } [\forall \Sigma ^{\prime \prime },\varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\cup _s\{\lnot \rho \}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime \prime }\Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })& \nonumber \\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}&\varTheta \cup _s \varTheta ^{\prime }]. \end{aligned}$$

  (13.7)

  By Fact 9, what we need to prove that comes down to

  $$ \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\lnot \rho \}\cup _s \varTheta ^{\prime }\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }). $$

  So suppose that $\Sigma ^{\prime \prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\lnot \rho \}\cup _s \varTheta ^{\prime \prime \prime }$, for some $\Sigma ^{\prime \prime \prime }$ and $\varTheta ^{\prime \prime \prime }$. We need to prove that $\Sigma \cup _s\Sigma ^{\prime \prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime \prime \prime })$. Instantiate (13.7) with $\Sigma ^{\prime }=\Sigma ^{\prime \prime \prime }$ and $\varTheta ^{\prime }=\varTheta ^{\prime \prime \prime }$.

  $$\begin{aligned}\forall \Sigma ^{\prime \prime },\varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\cup _s\{\lnot \rho \}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime \prime }\Rightarrow \Sigma ^{\prime \prime \prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime \prime \prime }\cup _s \varTheta ^{\prime \prime })&\\ \Rightarrow \Sigma \cup _s & \Sigma ^{\prime \prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime \prime \prime }.\nonumber \end{aligned}$$

  It suffice thus to prove the antecedent of this implication. So, for arbitrary $\Sigma ^{\prime \prime }$ and $\varTheta ^{\prime \prime }$, we need to show that

  $$ \Sigma ^{\prime \prime }\cup _s\{\lnot \rho \}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime \prime }\Rightarrow \Sigma ^{\prime \prime \prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime \prime \prime }\cup _s \varTheta ^{\prime \prime }. $$

  This is obtained by applying transitivity (Fact 8) on $\Sigma ^{\prime \prime }\cup _s\{\lnot \rho \}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime \prime }$ and the supposition $\Sigma ^{\prime \prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{\lnot \rho \}\cup _s \varTheta ^{\prime \prime \prime }$.

• Where ${\textbf {L}}$ is ${\textbf {K3}}$ or ${\textbf {CL}}$: $(v_{ST}(\rho ))^l\subseteq no(v_F(\rho ))$. Similar to the proof of the previous item.

Lemma 7

Suppose $A\notin \varTheta$ and $A\notin \Sigma$. If,

$$ \text {for all }\Sigma \text { and }\varTheta , \Sigma \rhd \varTheta \in |A|\text { iff }\Sigma \vdash _{\textbf{L}^{\textbf{e}}} A,\varTheta $$

then,

$$ \text {for all }\Sigma \text { and }\varTheta , \Sigma \rhd \varTheta \in no(|A|)\text { iff }\Sigma , A\vdash _{\textbf{L}^{\textbf{e}}} \varTheta . $$

Proof

Suppose that $A\notin \varTheta$ and $A\notin \Sigma$ and that $\Sigma \rhd \varTheta \in |A|$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} A,\varTheta$. We prove that ($\Sigma \rhd \varTheta \in no(|A|)$ iff $\Sigma , A\vdash _{\textbf{L}^{\textbf{e}}} \varTheta$).

Left to right Suppose $\Sigma \rhd \varTheta \in no(|A|)$, whence $\forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\rhd \varTheta ^{\prime }\in |A| \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime })$. When we instantiate $\Sigma ^{\prime }$ and $\varTheta ^{\prime }$ by $\{A\}$ resp. $\emptyset$, we obtain that $\Sigma \cup _s \{A\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta$.

Right to left Suppose $\Sigma , A\vdash _{\textbf{L}^{\textbf{e}}} \varTheta$ and therefore $\Sigma \cup _s \{A\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta$. We need to prove that

$$\begin{aligned} \forall \Sigma ^{\prime },\varTheta ^{\prime } (\Sigma ^{\prime }\rhd \varTheta ^{\prime }\in |A| \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }).\nonumber \end{aligned}$$

$\Sigma ^{\prime }\rhd \varTheta ^{\prime }\in |A|$ implies $\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\{A\}\cup _s\varTheta ^{\prime }$ by the main supposition. With the transitivity of $\vdash _{\textbf{L}^{\textbf{e}}}$, the latter combined with $\Sigma \cup _s \{A\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta$ allows us to derive $\Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }$.

Lemma 8

Central property of the canonical model.

Let M be the canonical ${\textbf{L}^{\textbf{r}}}$-model. $\Sigma \rhd \varTheta \in |A|_M$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{A\}\cup _s\varTheta$.

Proof

The proof goes by mathematical induction on the complexity of A.

Base case We have to prove the lemma for $A=\rho$, $A=\lnot \rho$, $A=\Box \rho$, and $A=\Box \lnot \rho$. This is evident in view of the clauses for $|\rho |$, $|\lnot \rho |$, $|\Box \rho |$, and $|\Box \lnot \rho |$, the definition of the $v_i$ ($1\le i \le 4$) in the canonical model and the fact that, for all ${\textbf{L}^{\textbf{r}}}$-models $M^{\prime }$, $|A|_{M^{\prime }}=|A|^l_{M^{\prime }}$.

Induction step Assume that $\Sigma \rhd \varTheta \in |A|_M$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{A\}\cup _s\varTheta$ for all formulas A of a complexity lower than c.

• $\Sigma \rhd \varTheta \in |B\wedge C|$ iff¹⁹ $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{B\wedge C\}\cup _s\varTheta$ ($\Rightarrow$) Suppose $\Sigma \rhd \varTheta \in |B\wedge C|$. By the semantics clause for $\wedge$ we get $\Sigma \rhd \varTheta \in (|B|\sqcup |C|)^l$. By Fact 10,

  $$\begin{aligned}\forall \Sigma ^{\prime }\forall \varTheta ^{\prime } [\forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\sqcup |C|) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })&\\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta &\cup _s \varTheta ^{\prime }].\nonumber \end{aligned}$$

  Take $\Sigma ^{\prime }=\emptyset$ and $\varTheta ^{\prime }=\{B\wedge C\}$. We get

  $$ \forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\sqcup |C|) \Rightarrow \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\wedge C\}\cup _s \varTheta ^{\prime \prime }) \Rightarrow \Sigma \vdash _{\textbf{L}^{\textbf{e}}}\{B\wedge C\}\cup _s\varTheta . $$

  This means that, in order to show this direction of this case, it suffices to prove

  $$ \forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\sqcup |C|) \Rightarrow \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\wedge C\}\cup _s \varTheta ^{\prime \prime }). $$

  So suppose

  $$ \Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\sqcup |C|). $$

  Hence, by the definition of $\sqcup$, for some $\Sigma _1^{\prime \prime }$, $\Sigma _2^{\prime \prime }$, $\varTheta _1^{\prime \prime }$ and $\varTheta _2^{\prime \prime }$ such that $\Sigma ^{\prime \prime }= \Sigma _1^{\prime \prime }\cup _s\Sigma _2^{\prime \prime }$ and $\varTheta ^{\prime \prime }= \varTheta _1^{\prime \prime }\cup _s\varTheta _2^{\prime \prime }$,

  $$ \Sigma _1^{\prime \prime }\rhd \varTheta ^{\prime \prime }_1\in |B|\text { and }\Sigma ^{\prime \prime }_2\rhd \varTheta _2^{\prime \prime }\in |C|. $$

  By the induction hypothesis

  $$ \Sigma _1^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\}\cup _s\varTheta ^{\prime \prime }_1 \text { and }\Sigma ^{\prime \prime }_2\vdash _{\textbf{L}^{\textbf{e}}}\{C\}\cup _s\varTheta _2^{\prime \prime }. $$

  Then, by the R$\wedge$-rule,

  $$ \Sigma _1^{\prime \prime }\cup _s\Sigma ^{\prime \prime }_2\vdash _{\textbf{L}^{\textbf{e}}}\{B\wedge C\}\cup _s\varTheta _1^{\prime \prime }\cup _s\varTheta _2^{\prime \prime }, $$

  whence finally

  $$ \Sigma \vdash _{\textbf{L}^{\textbf{e}}}\{B\wedge C\}\cup _s\varTheta . $$

  ($\Leftarrow$) Suppose that $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{B\wedge C\}\cup _s\varTheta$. We need to prove that

  $$\begin{aligned}\forall \Sigma ^{\prime }\forall \varTheta ^{\prime } [\forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\sqcup |C|) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })&\\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta &\cup _s \varTheta ^{\prime }].\nonumber \end{aligned}$$

  So suppose that

  $$ \forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\sqcup |C|) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime }). $$

  Instantiating $\Sigma ^{\prime \prime }$ with $\{B, C\}$ and $\varTheta ^{\prime \prime }$ with $\emptyset$ give us

  $$ \{B,C\}\rhd \emptyset \in (|B|\sqcup |C|) \Rightarrow \Sigma ^{\prime }\cup _s \{B,C\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta '. $$

  The induction hypothesis gives us $\{B\}\rhd \emptyset \in |B|$ because $B\vdash _{\textbf{L}^{\textbf{e}}}B$, and $\{C\}\rhd \emptyset \in |C|$ because $C\vdash _{\textbf{L}^{\textbf{e}}}C$, and therefore also $\{B,C\}\rhd \emptyset \in (|B|\sqcup |C|)$ by the definition of $\sqcup$, whence

  $$ \Sigma ^{\prime }\cup _s\{B,C\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime } $$

  By the $L\wedge$-rule, we get

  $$ \Sigma ^{\prime }\cup _s\{B\wedge C\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }. $$

  By the supposition and the transitivity of $\vdash _{\textbf{L}^{\textbf{e}}}$, we get

  $$ \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }. $$

• $\Sigma \rhd \varTheta \in |B\vee C|$ iff $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{B\vee C\}\cup _s\varTheta$ ($\Rightarrow$) Suppose $\Sigma \rhd \varTheta \in |B\vee C|$. By the semantics clause for $\vee$ we get $\Sigma \rhd \varTheta \in (|B|\cup |C|)^l$. By Fact 10,

  $$\begin{aligned}\forall \Sigma ^{\prime }\forall \varTheta ^{\prime } [\forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })&\\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta &\cup _s \varTheta ^{\prime }].\nonumber \end{aligned}$$

  Take $\Sigma ^{\prime }=\emptyset$ and $\varTheta ^{\prime }=\{B\vee C\}$. We get

  $$ \forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma {\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\vee C\}\cup _s \varTheta ^{\prime \prime }) \Rightarrow \Sigma \vdash _{\textbf{L}^{\textbf{e}}}\{B\vee C\}\cup _s\varTheta . $$

  This means that it suffices to prove

  $$ \forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\wedge C\}\cup _s \varTheta ^{\prime \prime }). $$

  So suppose $\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\cup |C|)$, in other words

  $$ \Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in |B|\quad \text {or}\quad \Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in |C|. $$

  By the induction hypothesis

  $$ \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\}\cup _s\varTheta ^{\prime \prime } \quad \text {or}\quad \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{C\}\cup _s\varTheta ^{\prime \prime }. $$

  Then, by the R$\vee$1-rule and the R$\vee$2-rule,

  $$ \Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\{B\vee C\}\cup _s\varTheta ^{\prime \prime }. $$

  ($\Leftarrow$) Suppose that $\Sigma \vdash _{\textbf{L}^{\textbf{e}}} \{B\vee C\}\cup _s\varTheta$. We need to prove that

  $$\begin{aligned} \forall \Sigma ^{\prime }\forall \varTheta ^{\prime } [\forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime })&\\ \Rightarrow \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta &\cup _s \varTheta ^{\prime }].\nonumber \end{aligned}$$

  So suppose that

  $$ \forall \Sigma ^{\prime \prime }\forall \varTheta ^{\prime \prime } (\Sigma ^{\prime \prime }\rhd \varTheta ^{\prime \prime }\in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime }\cup _s\Sigma ^{\prime \prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\cup _s \varTheta ^{\prime \prime }). $$

  First instantiating $\Sigma ^{\prime \prime }$ with $\{B\}$ and $\varTheta ^{\prime \prime }$ with $\emptyset$, and then instantiating $\Sigma ^{\prime \prime }$ with $\{C\}$ and $\varTheta ^{\prime \prime }$ with $\emptyset$, give us

  $$\begin{aligned} {} & {} {[\{B\}\rhd \emptyset \in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime }\cup _s \{B\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }]}\quad \text {and}\nonumber \\ {} & {} {[\{C\}\rhd \emptyset \in (|B|\cup |C|) \Rightarrow \Sigma ^{\prime }\cup _s \{C\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }]}.\nonumber \end{aligned}$$

  The induction hypothesis gives us $\{B\}\rhd \emptyset \in |B|$ because $B\vdash _{\textbf{L}^{\textbf{e}}}B$, and $\{C\}\rhd \emptyset \in |C|$ because $C\vdash _{\textbf{L}^{\textbf{e}}}C$, whence

  $$ \Sigma ^{\prime }\cup _s\{B\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }\text { and }\Sigma ^{\prime }\cup _s\{C\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime } $$

  By the $L\vee$-rule, we get

  $$ \Sigma ^{\prime }\cup _s\{B\vee C\}\vdash _{\textbf{L}^{\textbf{e}}}\varTheta ^{\prime }. $$

  By the supposition and the transitivity of $\vdash _{\textbf{L}^{\textbf{e}}}$, we get

  $$ \Sigma \cup _s\Sigma ^{\prime }\vdash _{\textbf{L}^{\textbf{e}}}\varTheta \cup _s \varTheta ^{\prime }. $$

• The other cases ($\lnot \lnot$, $\bot$, &, $\Box \vee$, $\Box \wedge$, $\Box \lnot \lnot$) do not introduce any new difficulties.

Theorem 5

Completeness. If $A_1\ldots A_n\vDash _{\textbf{L}^{\textbf{e}}} B_1\ldots B_m$ then $A_1\ldots A_n\vdash _{\textbf{L}^{\textbf{e}}}B_1\ldots B_m$.

Proof

We prove the contraposition of this theorem. Suppose $A_1\ldots A_n\not \vdash _{\textbf{L}^{\textbf{e}}}B_1\ldots B_m$. Then, for arbitrary distinct sentential letters²⁰ $\rho _1\ldots \rho _n$ and $\sigma _1\ldots \sigma _m$ not occurring in the $A_i$ ($i\le n$) or $B_j$ ($j\le m$),

$$ A_1 \& \rho _1 \ldots A_n \& \rho _n \not \vdash _{\textbf{L}^{\textbf{e}}}B_1\vee \sigma _1\ldots B_m\vee \sigma _m. $$

Then, by the R$\bot$-rule also

$$ A_1 \& \rho _1 \ldots A_n \& \rho _n \not \vdash _{\textbf{L}^{\textbf{e}}}\bot , B_1\vee \sigma _1\ldots B_m\vee \sigma _m. $$

Let M be the canonical ${\textbf{L}^{\textbf{r}}}$-model. By Lemma 8, we obtain

But, in light of the definition of $\sqcup$ in the canonical model and the fact that $A\rhd \emptyset \in |A|$ and $\emptyset \rhd B\in no|B|$, we know that (omitting the subscript M from expressions of the form $|A|_M$),

$$ \begin{aligned} A_1 \& \rho _1, &\ldots , A_n \& \rho _n \rhd B_1\vee \sigma _1,\ldots ,B_m\vee \sigma _m \in \\ {} &(|A_1 \& \rho _1|\sqcup ^l \ldots \sqcup ^l |A_n \& \rho _n|\sqcup ^l no(|B_1\vee \sigma _1|)\sqcup ^l \ldots \sqcup ^l no(|B_m\vee \sigma _m|)).\nonumber \end{aligned}$$

By the clauses for $|A \& B|$ and $|A\vee B|$

So, by ($\heartsuit$) and ($\ddag$), we have that

$$ (|A_1|\sqcup ^l \ldots \sqcup ^l |A_n|\sqcup ^l no(|B_1|)\sqcup ^l \ldots \sqcup ^l no(|B_m|))\not \subseteq |\bot |, $$

which is equivalent to $A_1\ldots A_n\not \vDash _{\textbf{L}^{\textbf{e}}} B_1\ldots B_m$.