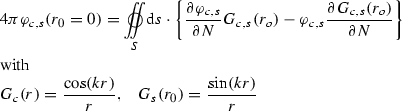Skip to main content
SpringerLink
Log in

Kirchhoff’s theory for optical diffraction, its predecessor and subsequent development: the resilience of an inconsistent theory

  • Published:
Archive for History of Exact Sciences Aims and scope Submit manuscript

Abstract

Kirchhoff’s 1882 theory of optical diffraction forms the centerpiece in the long-term development of wave optics, one that commenced in the 1820s when Fresnel produced an empirically successful theory based on a reinterpretation of Huygens’ principle, but without working from a wave equation. Then, in 1856, Stokes demonstrated that the principle was derivable from such an equation albeit without consideration of boundary conditions. Kirchhoff’s work a quarter century later marked a crucial, and widely influential, point for he produced Fresnel’s results by means of Green’s theorem and function under specific boundary conditions. In the late 1880s, Poincaré uncovered an inconsistency between Kirchhoff’s conditions and his solution, one that seemed to imply that waves should not exist at all. Researchers nevertheless continued to use Kirchhoff’s theory—even though Rayleigh, and much later Sommerfeld, developed a different and mathematically consistent formulation that, however, did not match experimental data better than Kirchhoff’s theory. After all, Kirchhoff’s formula worked quite well in a specific approximation regime. Finally, in 1964, Marchand and Wolf employed the transformation of Kirchhoff’s surface integral that had been developed by Maggi and Rubinowicz for other purposes. The result yielded a consistent boundary condition that, while introducing a species of discontinuity, nevertheless rescued the essential structure of Kirchhoff’s original formulation from Poincaré’s paradox.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. Kirchhoff (1882), also printed as Kirchhoff (1883). In this article, we use an English translation by Hentschel and Zhu (forthcoming).

  2. Kuhn (1962), pp. 10–34.

  3. Poincaré (1892b), pp. 187–188.

  4. According to Werner Marx’s bibliometric analysis, Kirchhoff’s 1882 work from 1900 to 2010 has been specifically cited 70 times in research articles; moreover, the citation count has increased over the years: Marx (2016).

  5. Schweber (1994)

  6. Bloor (2011).

  7. Klaus Hentschel, Ning Yan Zhu, Ann Hentschel, and Werner Marx have provided a comprehensive historical study of Kirchhoff’s 1882 paper by translating it into English, presenting a commentary, situating it within Kirchhoff’s intellectual biography, and conducting a scientometric analysis of citations to it: Hentschel and Zhu (forthcoming). In light of the realism debate in philosophy of science, Juha Saatsi and Peter Vickers have used Kirchhoff’s theory as a counterexample to primitive realism—what they have termed “naïve optimism”—which contends that any significant novel predictive success can be explained by the truth content of the assumptions that play an essential role in the derivation. Kirchhoff’s boundary conditions, Saatsi and Vickers noted, are both mathematically inconsistent and physically untenable. Yet they are essential assumptions for the derivation of Kirchhoff’s empirically-successful (within certain regimes) formula (Saatsi and Vickers 2011). We thank Ning Yan Zhu for catching a number of misprints and missing or incorrect references in a previous version of the present article.

  8. On the history of Huygens’ optics and its background see Shapiro (1973). On Young see Kipnis (1991), and on Fresnel see Buchwald (1989).

  9. For full details see Buchwald (1989), Chap. 6.

  10. See, for example, Kong (1986), pp. 671–695

  11. Herschel (1827), Sec. 623.

  12. For the example of dispersion and Augustin Cauchy’s (1789–1857) elaborate mathematics see Buchwald (2012). For a broad overview of the period see Buchwald (2013) and Darrigol (2012).

  13. Stokes (1856); reprinted in Stokes (1883), pp. 243–328.

  14. Ibid., 243–244.

  15. Stokes (1845c). Of course neither Stokes nor anyone else, with the partial exception of James Clerk Maxwell (1831–1879), used vector notation until the 1890s. Nevertheless physicists and mathematicians of the period were able almost at once to produce the component equivalents of even complex vector operations, so that modern notation does not unduly alter their original understanding.

  16. It is particularly ironic that Stokes took this from Poisson, because he at once used it to argue that the inclination factor varies in a fashion that Poisson himself would probably not have (Buchwald (1989), p. 192).

  17. On which see Baker and Copson (1939), pp. 12–15.

  18. Stokes was a bit disingenuous here, since not only his investigation, but Poisson’s solution, requires the limitation. Stokes’ quick attempt to extend the class of allowable functions to cover those which are not temporally delimited requires a great deal more justification than this Stokes (1883), pp. 278.

  19. Stokes set the compression wave to the side. However, the mechanically-necessary existence of both compression and distortion generally posed a problem for such investigations because they cannot easily be divorced from one another, particularly if the model involves, like Cauchy’s, forces between particles [on which see Buchwald (1980, 1981)]. Cauchy assumed the compression wave to be invisible (which raised energy issues that might in principle be detectable), while Stokes took the compression constant to be so large that the corresponding wave speed was infinitely larger than the speed of the distortional wave, implying that the former would not be visible or otherwise affect the latter. This amounted to assuming that the ether is incompressible, requiring the rate of displacement \(\partial \vec {u}/\partial t\) of any element to satisfy \(\nabla \cdot \partial \vec {u}/\partial t=0\).

  20. Green (1828).

  21. After Peter Lejeune Dirichlet, 1805–1859; cf Riemann (1857), p. 17.

  22. Stokes (1845a, b).

  23. Of course optical polarization required the existence of transverse oscillations, i.e. of \(\nabla \times \vec {v}\), and so Stokes emphasized that irrotationality could hold only for “that part of the motion of the ether which is due to the motion of translation of the earth and planets” (ibid., p. 137).

  24. Lorentz (1887).

  25. Named after the German mathematician Carl Neumann (1832–1925). For histories of the boundary-value criteria for harmonic functions see Cross (1985); Cheng and Cheng 2005). See Kline (1972), Chap. 28 for an overview of partial differential equations in the period.

  26. Jungnickel and McCormmach (1986), pp. 30–32, Vol. 2.

  27. Kirchhoff (1883), cf pp. 663. The paper was included in the posthumous publication of Kirchhoff’s works: Kirchhoff (1891a), pp. 22–54.

  28. Ibid., 665.

  29. Kirchhoff (1876), pp. 314–317. There Kirchhoff had used a different specification for the limits in his time integral with attendant changes in the argument which was however less detailed than it later became, perhaps because Kirchhoff wanted to ensure the analysis would work for an infinite train of disturbances (see below).

  30. Kirchhoff (1883), p. 666.

  31. Kirchhoff (1891b), pp. 24–25. Note that the requirement that the integration limits of F must be “finite positive and negative” is maintained. He had first developed an argument for the existence of F in his 1876 derivation for propagation in a compressible fluid. This addenda to the original specification of the function F was added by the editor, Kurt Hensel (1861–1941), of the Optik (Kirchhoff 1891b, p. 267), indicating the existence of disquiet concerning the function. We thank Ning Yan Zhu for noting Hensel’s intervention.

  32. Ibid., pp. 666–668.

  33. At time zero because F(at) is itself non-zero only when its argument vanishes.

  34. Ibid., 668–669.

  35. Helmholtz, “Theorie der Luftschwingungen in Röhren mit offenen Enden,” Journal für die reine und angewandte Mathematik, 62:1 (1859), 23. Suppose with Helmholtz that

    \(\varphi (\vec {r},t)=\varphi _c (\vec {r})\cos (\omega t)+\varphi _s (\vec {r})\sin (\omega t)\) so that the time and space dependencies could be separated. Helmholtz’s equation may then be written as follows:

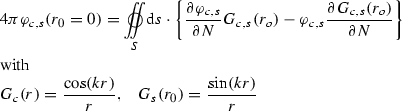
  36. Ibid., pp. 669–670. The translation is by Anne Hentschel in Hentschel and Zhu (forthcoming).

  37. Kirchhoff’s requirement was in later years subsumed under what became known as the Sommerfeld radiation condition, according to which the limit at infinity of the difference \(\partial \varphi /\partial N-2\pi i\varphi /\lambda \) must vanish: cf Goodman (1988), p. 44.

  38. Kirchhoff expressed this as the wavelength being ‘infinitesimal’ and the sum \(r_{o},r_{i}\) being effectively constant throughout the integration since the limitation to a second-order expansion restricts the integration’s accuracy to loci within the vicinity of the origin, where the sum is a minimum (Kirchhoff 1883, p. 672).

  39. Ibid., pp.683–685.

  40. Given these boundary conditions, and a special condition, Kirchhoff could also retrieve geometric optics. Require that the sum of the distances from I and O to the surface must not be constant for any finite part of it—meaning in effect that both the observation and luminous points are very far away. If, under this condition, the line joining I to O does not anywhere intersect a body that does not reflect light—a “black body”—then the wave at O remains unaltered. If, on the other hand, that line passes through the black body at least once, then “darkness occurs at the location of O,” a true shadow is formed and in consequence “the light from the luminous point propagates rectilinearly in rays that can be regarded as independent of one another” (ibid., pp. 686–687). This retrieves geometric optics for a black-body obstacle and an effectively infinitesimal wavelength. The limitation to constancy over a finite area of the surface for the sum \(r_o +r_i \) is dropped for diffraction.

  41. Ibid., p. 688. Note that \({\partial r_i }/{\partial N}=\cos (\vec {r}_i ,\vec {n}_i )\) and \({-\partial r_o }/{\partial N}=\cos (\vec {r}_o ,\vec {n}_o )\), where \(\vec {r}_i \) is the vector from an arbitrary point on A to the point of illumination I, \(\vec {r}_o \) is the vector from the same point on A to the point of observation O, \(\vec {n}_i \) is the vector normal to A and pointing toward the side of I, \(\vec {n}_o \) is the vector normal to A and pointing toward the side of O, and \(\cos (\vec {a},\vec {b})\) is the cosine of the angle between the two vectors \(\vec {a}\) and \(\vec {b}\). Kirchhoff’s diffraction integral may thereby be written as

    \(\varphi _o =\frac{1}{2\lambda }\mathop {\int \!\!\!\int }\limits _{A} {\frac{\mathrm{d}s}{r_i r_o }\left[ {\cos (\vec {r}_i ,\vec {n}_i )+\cos (\vec {r}_o ,\vec {n}_o )} \right] \sin \left[ {2\pi \left( {\frac{r_i +r_o }{\lambda }-\frac{t}{T}} \right) } \right] } \).

  42. Fresnel took the wave in Huygens’ principle to differ from the source wave solely by virtue of distance to the surface of integration, so that, e.g., a cosine wave remained a cosine wave plus a phase addition to its argument. However, the integrands in Kirchhoff’s expression are shifted by a quarter wavelength from the source wave in addition to the phase addition. The shift is a direct consequence of applying Green’s theorem to the wave equation.

  43. Kirchhoff (1883), p. 689.

  44. For a thorough account of Poincaré’s life and career see Gray (2013). Also Dieudonné (2008); Charpentier et al. 2010). On anomalous dispersion and its theoretical consequences see Buchwald (1985), chap. 27.

  45. Poincaré had derived formulae akin to Kirchhoff’s in the 1887–1888 lectures, though at that time he was unaware of Kirchhoff’s theory; he had then also noted that the boundary conditions cannot strictly hold at the same time: Poincaré (1889), pp. 115–116. On Poincaré and light see Darrigol (2015).

  46. Poincaré (1892b), pp. 141–143.

  47. Poincaré always presumed an outer surface \(S_\infty \) at infinity at which the wave function \(\varphi \) and its normal derivative vanish, with the surfaces \(\sigma _k \) forming inner boundaries. The Green’s function at point U is \(G_P=\exp (-ikr_P)/r_P\), where \(r_P\) is the distance between U and \(P,k=2\pi /\lambda \) and the time dependence has been removed due to the monochromatic assumption.

  48. Poincaré’s deduction of the difficulty is extremely terse. What follows draws out the several relations that he developed in somewhat greater detail. Also see Baker and Copson (1939), pp. 70–72.

  49. Poincaré (1889), pp. 144–145.

  50. Marchand and Wolf (1966), p. 1712.

  51. Hyperbolic equations, of which the time-dependent wave equation is one, have the form

    \({\partial ^{2}\varphi }/{\partial x^{2}-\left( {1/{c^{2}}} \right) }{\partial ^{2}\varphi }/{\partial t^{2}}=f(x,t)\) while elliptic equations satisfy

    \({\partial ^{2}\varphi }/{\partial x^{2}+}{\partial ^{2}\varphi }/{\partial y^{2}}=f(x,y)\)—Laplace’s, Poisson’s and the time-independent wave equation developed by Helmholtz are all elliptic.

  52. Poincaré (1892b), p. 188.

  53. Rayleigh (1897). The details of Rayleigh’s analysis depended upon results he had developed in his Theory of Sound, whose second edition of the first volume had appeared in 1894 and, for the relevant parts of the second volume, the year before.

  54. Rayleigh (1896), secs. 277, 278 and 292, the last of which Rayleigh referred to in his paper on optical diffraction, Rayleigh 1897.

  55. Sommerfeld (1896); translated as Sommerfeld (2004).

  56. For a comprehensive examination of the Sommerfeld school at Munich, and in particular its concentration on the solution of specific problems, see Seth (2010).

  57. Sommerfeld (1895), pp. 341–342.

  58. In 1892 Poincaré had himself considered the case of diffraction from a sharp metallic edge at large diffraction angles in an effort to account for experimental results that Gouy had obtained (Gouy (1886)). To do so he limited his analysis to infinite conductivity and examined the two-dimensional case by considering the wave from the edge produced by the scattering of a converging cylindrical disturbance whose axis parallels the edge (Poincaré (1892a); on this and Gouy’s experiments see Darrigol (2015), pp. 14–16.) Sommerfeld referred to Poincaré’s results for support since he had obtained a similar final expression under the same approximation (far field close to the edge of the geometric shadow): Sommerfeld 1896, p. 374.

  59. Sommerfeld produced a version of his theory in his lectures on optics: Sommerfeld (1954) present the lectures that he gave in 1934. Secs. 38–39 provide his “mathematically rigorous solution” for the infinitely-thin, semi-infinite screen. See Born and Wolf (2002); chap. 11 develops the Sommerfeld theory up to the early 1950s. For subsequent developments see Babich et al. (2007).

  60. Sommerfeld (1954), pp. 195–201. Sommerfeld had likely been giving these lectures for decades in some form, so that his version of the Rayleigh alternatives probably date to his early years at Munich, so a decade or more after Rayleigh’s work on the subject. Sommerfeld did not mention Rayleigh in the published lectures, perhaps because his version of the alternatives involved a considerably different Green’s function, as we shall see.

  61. Ibid., 198–200.

  62. For \(\varphi ^{I}\)the normal derivative of the Sommerfeld difference Green’s function reduces to twice the value of the positive term, while for \(\varphi ^{II}\)the Sommerfeld function is just twice the value of either term.

  63. Rayleigh (1913).

  64. Sommerfeld (1896), p. 374.

  65. Sommerfeld (1954), p. 200. The italics are Sommerfeld’s.

  66. Maggi (1888). On Maggi see Cisotti (1938), Anonymous, 2015. The reminiscence is from Maggi (1914). Maggi wrote the latter paper in order to compensate the difficulty of his 1888 presentation which, he wrote in 1914, “had somewhat harmed its perspicuity.”

  67. Maggi (1914). Since Kirchhoff died in 1887, Maggi’s “not long before” means several years prior to 1888.

  68. On which see Buchwald (1994), chap. 8.

  69. The fact that the addition by Hensel in the published lectures a few years later writes of F that such a function “actually” exists may indicate doubt at the time concerning the propriety of basing such a fundamental result upon it.

  70. Eckert (2013), p. 226.

  71. Rubinowicz (1917).

  72. In 1923, the Austrian professor of physics Friedrich Kottler at the University of Vienna pointed out that Maggi, not Rubinowicz, had first produced the transformation. See Kottler (1923).

  73. Rubinowicz (1917), p. 259.

  74. Ibid., p. 260.

  75. Ibid., p. 259.

  76. Partial only because Young had assumed that the wave emanating from the aperture’s rim would be the same as the source wave but shifted in phase by half a wavelength. Rubinowicz’s rim integral is considerably different.

  77. Kottler (1923) and, decades later, Kottler 1965.

  78. By contrast, in electro- and magneto-statics dielectric and para- or dia-magnetic substances yield the discontinuity as a result of the jump in permeability at a boundary.

  79. Born (1933), p. 152.

  80. Marchand and Wolf (1964).

  81. The expression given immediately above is not applicable to a point close to the aperture because of the assumption that the aperture point to observation point distance is vastly larger than a wavelength. If however we take as an example of the problem what occurs in the case of a circular disk as screen and make no approximations, then two problems arise using the full Kirchhoff integral. The solution along the axis produces two terms, the second of which is infinite and obviously unphysical. Moreover—and this is the sort of problem that Marchand and Wolf had in mind—even the first term does not vanish at the disk itself, where by hypothesis no wave at all should exist. In other words, the boundary condition presupposed cannot be recovered (see Lucke 2004, pp. 3–4). A similar situation arises for diffraction by a circular aperture, in which the incident wave is not recovered at the aperture.

  82. Marchand and Wolf (1966).

  83. Neither are these results accommodated by the Rayleigh-Sommerfeld alternative in which the waveform at the aperture is assumed to be the same as that of the incident disturbance. The second alternative, in which the waveform’s normal derivative is specified, fares somewhat better but still misses the mark. Ibid., pp. 1715–1717.

  84. Michelson and Pease (1920).

  85. Marchand and Wolf (1966), pp. 1715–1717.

  86. Sommerfeld (1954), p. 200.

References

  • Anonymous. 2015. Maggi, Gian Antonio. Treccani Enciclopedia Italiana. http://www.treccani.it/enciclopedia/gian-antonio-maggi/. Accessed 15 July 2015.

  • Babich, V.M., M.A. Lyalinov, and V.E. Grikurov. 2007. Diffraction theory: The Sommerfeld–Malyuzhinets technique. UK: Alpha Science Intl. Ltd.

    Google Scholar 

  • Baker, B., and E.T. Copson. 1939. The mathematical theory of Huygens’ principle. Oxford: Clarendon Press.

    MATH  Google Scholar 

  • Bloor, D. 2011. The enigma of the aerofoil: Rival theories in aerodynamics, 1909–1930. Chicago: University of Chicago Press.

    Book  Google Scholar 

  • Born, M. 1933. Optik. Berlin: Julius Springer-Verlag.

    Book  MATH  Google Scholar 

  • Born, M., and E. Wolf. 2002. Principles of optics. Cambridge: Cambridge University Press.

    Google Scholar 

  • Buchwald, J. 1980. Optics and the theory of the punctiform ether. Archive for History of Exact Sciences 21: 245–278.

    Article  MathSciNet  Google Scholar 

  • Buchwald, J. 1981. The quantitative ether in the first half of the nineteenth century. In Conceptions of ether: Studies in the history of ether theories, 1740–1900, ed. G. Cantor, and M.J.S. Hodge, 215–237. Cambridge: Cambridge University Press.

    Google Scholar 

  • Buchwald, J. 1985. From Maxwell to microphysics: Aspects of electromagnetic theory in the last quarter of the nineteenth century. Chicago: University of Chicago Press.

    Google Scholar 

  • Buchwald, J. 1989. The rise of the wave theory of light: Optical theory and experiment in the early nineteenth century. Chicago: University of Chicago Press.

    Google Scholar 

  • Buchwald, J. 1994. The creation of scientific effects: Heinrich Hertz and electric waves. Chicago: University of Chicago Press.

    Book  Google Scholar 

  • Buchwald, J. 2012. Cauchy’s theory of dispersion anticipated by Fresnel. In A master of science history, ed. J. Buchwald, 399–416. Dordrecht: Springer.

    Chapter  Google Scholar 

  • Buchwald, J. 2013. Optics in the Nineteenth Century. In The Oxford handbook of the history of physics, ed. J. Buchwald, and R. Fox, 445–472. Oxford: Oxford University Press.

    Google Scholar 

  • Charpentier, E., E. Ghys, and A. Lesne (eds.). 2010. The scientific legacy of Poincaré. Providence, RI: American Mathematical Society.

    MATH  Google Scholar 

  • Cheng, A.H.D., and D.T. Cheng. 2005. Heritage and early history of the boundary element method. Engineering Analysis with Boundary Elements 29: 268–302.

    Article  MATH  Google Scholar 

  • Cisotti, U. 1938. Gli scritti scientifici di Gian Antonio Maggi. Rendiconti del Seminario Matematico e Fisico di Milano 12: 167–189.

    Article  MATH  Google Scholar 

  • Cross, J.J. 1985. Integral theorems in Cambridge mathematical physics, 1830–55. In Wranglers and physicists: Studies on Cambridge mathematical physics in the nineteenth century, ed. P.M. Harman, 112–148. Manchester: Manchester University Press.

    Google Scholar 

  • Darrigol, O. 2012. A history of optics from Greek antiquity to the nineteenth century. Oxford: Oxford University Press.

    MATH  Google Scholar 

  • Darrigol, O. 2015. Poincaré’s Light. In Henri Poincaré, 1912–2012: Poincaré Seminar 2012, ed. B. Duplantier, and V. Rivasseau, 1–50. Basel: Springer.

    Google Scholar 

  • Dieudonné, J. 2008. Jules Hernri Poincaré: Complete dictionary of scientific biography. Detroit: Charles Scribner’s Sons.

    Google Scholar 

  • Eckert, M. 2013. Arnold Sommerfeld: Science, life and turbulent times, 1868–1951. New York: Springer.

    Book  MATH  Google Scholar 

  • Goodman, J.W. 1988. Introduction to fourier optics. New York: McGraw Hill.

    Google Scholar 

  • Gouy, L.G. 1886. Recherches experimentales sur la diffraction. Annales de chimie et de physique 52: 145–192.

    MATH  Google Scholar 

  • Gray, J. 2013. Henri Poincaré: A scientific biography. Princeton: Princeton University Press.

    MATH  Google Scholar 

  • Green, G. 1828. An essay on the application of mathematical analysis to the theories of electricity and magnetism: Mathematical papers of the late George Green. Cambridge: Cambridge University Press.

    Google Scholar 

  • Hentschel, K., and N. Zhu. Gustav Robert Kirchhoff’s treatise On the theory of light rays (1882) - English Translation, Analysis and Commentary. Stuttgarter Beiträge zur Wissenschafts- und Technikgeschichte. Berlin: Logos-Verlag (forthcoming).

  • Herschel, J. 1827. Light. Encyclopedia Metropolitana, 341–586.

  • Jungnickel, C., and R. McCormmach. 1986. Intellectual mastery of nature: Theoretical physics from Ohm to Einstein. Chicago: University of Chicago Press.

    MATH  Google Scholar 

  • Kipnis, N. 1991. History of the principle of interference of light. Basel: Birkhäuser.

    Book  MATH  Google Scholar 

  • Kirchhoff, G. 1876. Vorlesungen über mathematische Physik, Bd 1: Mechanik. Leipzig: B. G. Teubner.

    MATH  Google Scholar 

  • Kirchhoff, G. 1882. Zur Theorie der Lichtstrahlen. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin part 2: 641–669.

    MATH  Google Scholar 

  • Kirchhoff, G. 1883. Zur Theorie der Lichtstrahlen. Annalen der Physik 255: 663–695.

    Article  MATH  Google Scholar 

  • Kirchhoff, G. 1891a. Gesammelte Abhandlungen von G. Kirchhoff. Leipzig: J. A. Barth.

    MATH  Google Scholar 

  • Kirchhoff, G. 1891b. Vorlesungen über mathematische Physik, Optik. Leipzig: B. G. Teubner.

    MATH  Google Scholar 

  • Kline, M. 1972. Mathematical thought from ancient to modern times. New York: Oxford University Press.

    MATH  Google Scholar 

  • Kong, J.A. 1986. Electromagnetic wave theory. New York: Wiley.

    Google Scholar 

  • Kottler, F. 1923. Zur Theorie der Beugung an schwarzen Schirmen. Annalen der Physik 375: 405–456.

    Article  MATH  Google Scholar 

  • Kottler, F. 1965. Diffraction at a black screen: Part I: Kirchhoff’s Theory. Progress in Optics 4: 283–314.

    Google Scholar 

  • Kuhn, T. 1962. The structure of scientific revolutions. Chicago: University of Chicago Press.

    Google Scholar 

  • Lorentz, H.A. 1887. De l’influence du mouvement de la terre sur les phénomènes lumineux. Archives Néerlandaises 21: 103–176.

    MATH  Google Scholar 

  • Lucke, R.L. 2004. Rayleigh-Sommerfeld diffraction vs Fresnel-Kirchhoff, Fourier propagation, and Poisson’s spot. NRL/FR/7218–04–10,101. Washington, DC: Naval Research Laboratory.

    Google Scholar 

  • Maggi, G.A. 1888. Sulla propagazione libera e perturbata delle onde luminose in un mezzo isotropo. Annali di Matematica Pura ed Applicata 16: 21–48.

    Article  MATH  Google Scholar 

  • Maggi, G.A. 1914. Sul teorema di Kirchhoff traducente il principio di Huygens. Annali di Matematica Pura ed Applicata 22: 171–177.

    Article  MATH  Google Scholar 

  • Marchand, E.W., and E. Wolf. 1964. Comparison of the Kirchhoff and the Rayleigh-Sommerfeld theories of diffraction at an aperture. Journal of the Optical Society of America 54: 587–594.

    Article  MathSciNet  Google Scholar 

  • Marchand, E.W., and E. Wolf. 1966. Consistent formulation of Kirchhoff’s diffraction theory. Journal of the Optical Society of America 56: 1712–1722.

    Article  Google Scholar 

  • Marx, W. 2016. Bibliometric analysis of Kirchhoff’s paper. Gustav Robert Kirchhoff’s Treatise On the Theory of Light Rays (1882) [forthcoming]

  • Michelson, A., and F.G. Pease. 1920. Measurement of the diameter of \(\alpha \) Orionis with the interferometer. Contributions from the Mount Wilson Observatory 203: 249–260.

    Google Scholar 

  • Poincaré, H. 1889. Leçons sur la Théorie Mathématique de la Lumière, professés pendant le premier semestre 1887–1888. Paris: Georges Carré.

    Google Scholar 

  • Poincaré, H. 1892a. Sur la polarisation par diffraction. Acta Mathematica 16: 1–50.

    Article  MathSciNet  Google Scholar 

  • Poincaré, H. 1892b. Théorie mathématique de la lumière II: Nouvelles études sur la Diffraction – Théorie de la dispersion de Helmholtz: Leçons professés pendant le premier semestre 1891–1892. Paris: Gauthier-Villars.

  • Rayleigh, 1896. Theory of sound. London: Macmillan and Co.

  • Rayleigh, 1897. On the passage of waves through apertures in plane screens, and allied problems. Philosophical Magazine 43: 259–272.

  • Rayleigh, 1913. On the passage of waves through fine slits in thin opaque screens. Proceedings of the Royal Society of London 89: 194–219.

  • Riemann, B. 1857. Theorie der Abel’schen Functionen. Berlin: Georg Reimer.

    Google Scholar 

  • Rubinowicz, A. 1917. Die Beugungswelle in der Kirchhoffschen Theorie der Beugungserscheinungen. Annalen der Physik 53: 257–278.

    Article  Google Scholar 

  • Saatsi, J., and P. Vickers. 2011. Miraculous success? Inconsistency and untruth in Kirchhoff’s diffraction theory. British Journal for the Philosophy of Science 10: 1–18.

    MATH  MathSciNet  Google Scholar 

  • Schweber, S.S. 1994. QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press: Princeton.

    MATH  Google Scholar 

  • Seth, S. 2010. Crafting the quantum: Arnold Sommerfeld and the practice of theory, 1890–1926. Cambridge: MIT.

    MATH  Google Scholar 

  • Shapiro, A. 1973. Kinematic optics: A study of the wave theory of light in the seventeenth century. Archive for History of Exact Sciences 11: 134–266.

    Article  MATH  MathSciNet  Google Scholar 

  • Sommerfeld, A. 1895. Zur mathematischen Theorie der Beugungserscheinungen. Nachrichten von der König. Gesellschaft der Wissenschaften zu Göttingen 1: 338–342.

    MATH  Google Scholar 

  • Sommerfeld, A. 1896. Mathematische Theorie der Diffraction. Mathematische Annalen 47: 317–374.

    Article  MATH  MathSciNet  Google Scholar 

  • Sommerfeld, A. 1954. Optics: Lectures on theoretical physics, vol. IV. New York: Academic Press.

    MATH  Google Scholar 

  • Sommerfeld, A. (ed.). 2004. Mathematical theory of diffraction. Basel: Birkhäuser.

    MATH  Google Scholar 

  • Stokes, G. 1845a. On the aberration of light. In Mathematical and physical papers, ed. G. Stokes, 134–140. Cambridge: Cambridge University Press.

    Google Scholar 

  • Stokes, G. 1845b. On the constitution of luminiferous ether, viewed with reference to the phenomenon of the aberration of light. In Mathematical and physical papers, ed. G. Stokes, 153–156. Cambridge: Cambridge University Press.

    Google Scholar 

  • Stokes, G. 1845c. On the theories of the internal friction of fluid in motion, and of the equilibrium and motion of elastic solids. In Mathematical and physical papers, ed. G. Stokes, 243–328. Cambridge: Cambridge University Press.

    Google Scholar 

  • Stokes, G. 1856. On the dynamical theory of diffraction. Transactions of the Cambridge Philosophical Society 9: 1–62.

    Google Scholar 

  • Stokes, G. 1883. Mathematical and physical papers. Cambridge: Cambridge University Press.

    MATH  Google Scholar 

Download references

Acknowledgments

We thank Diana Kormos Buchwald for her assistance in correcting errors.

Author information

Authors and Affiliations

  1. California Institute of Technology, Pasadena, CA, USA

    Jed Z. Buchwald

  2. Institute for the History and Philosophy of Science and Technology, University of Toronto, Toronto, Canada

    Chen-Pang Yeang

Authors
  1. Jed Z. Buchwald
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen-Pang Yeang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jed Z. Buchwald.

Additional information

Communicated by: Jed Buchwald.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buchwald, J.Z., Yeang, CP. Kirchhoff’s theory for optical diffraction, its predecessor and subsequent development: the resilience of an inconsistent theory. Arch. Hist. Exact Sci. 70, 463–511 (2016). https://doi.org/10.1007/s00407-016-0176-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00407-016-0176-1

Keywords

Search

Navigation